基于LSTM神经网络深度序列机械钻速实时预测
2024-01-22杨立军李慎越席俊卿
冯 义,朱 亮,杨立军,李慎越,席俊卿,陈 芳,纪 慧
(1.中石油吐哈油田分公司 工程技术研究院,新疆 哈密 839000; 2.油气钻完井技术国家工程研究中心,湖北 武汉 430100; 3.油气钻采工程湖北省重点实验室(长江大学),湖北 武汉 430100; 4.长江大学 石油工程学院,湖北 武汉 430100)
引言
机械钻速是单位纯钻进时间内的进尺量,钻速越大则钻井效率越高,能更快钻达油层[1-2]。准确预测机械钻速有助于精确规划钻井作业、缩短钻井周期、节省钻井成本[3-4]。如何挖掘和利用钻完井大量数据,为深部地层提供优质钻进提速方案,是目前钻井行业值得思考和待解决的重要问题[5-6]。
近年来,随着人工智能技术的飞速发展,智能算法的高效性和预测的准确性被挖掘,越来越多的学者将智能算法用于机械钻速预测,闫铁和Amer等[7-9]提出了基于人工神经模型进行机械钻速预测的新方法;宋先知等[10]基于支持向量机回归法进行机械钻速智能预测;Ahmed等[11]通过分析人工神经网络、支持向量机等智能模型的预测精度,验证了智能算法在机械钻速预测中的可行性。李琪等[12]提出一种优化算法和BP神经网络相结合的方法进行机械钻速预测。石祥超等[5]通过4种人工智能方法(随机森林、支持向量机、人工神经网络、梯度提升树)对某单井的预测结果表明,人工智能方法能够对单井或区块的机械钻速进行良好的预测。杨莉等[13]提出了模糊神经网络的预测模型解决机械钻速预测过程中的参数耦合问题,并验证了该模型的可行性和适用性。在数据规模较小的情况下这些模型具有较好的预测精度,但随着数据规模的不断扩大,这些算法由于模型结构浅,往往不能满足精度要求,而且这些算法容易陷入局部最优,预测结果稳定性差。深度学习中的长短期记忆(Long-term and Short-term Memory,LSTM)神经网络模型预测精度高且能有效克服以往方法中过拟合等问题[14],目前LSTM神经网络模型在复杂工程问题中应用广泛[15-18]。近两年来越来越多的石油人将LSTM神经网络模型用于解决石油工程中高精度预测问题,如薛亮等[19]将机器学习中的长短期记忆神经网络应用到气井生产动态分析中。潘少伟等[20]通过长短期记忆神经网络建立时间序列预测模型重新生成缺失的测井曲线,为后续的岩性识别奠定基础。蔺研锋等[21]用长短期记忆神经网络对井漏事故进行实时预测。何为等[22]用长短期记忆神经网络对催化裂化装置NOx排放进行预测。
针对目前在机械钻速预测方法上研究的不足,本文充分利用LSTM神经网络模型的预测优势,提出基于长短时记忆(LSTM)神经网络的深度序列机械钻速预测方法,并对优化前后的LSTM模型预测结果进行对比分析。
1 工作流程及数据采集
1.1 工作流程
本研究的工作流程包括数据处理、模型搭建、模型训练、结果评估4个阶段,如图1所示。
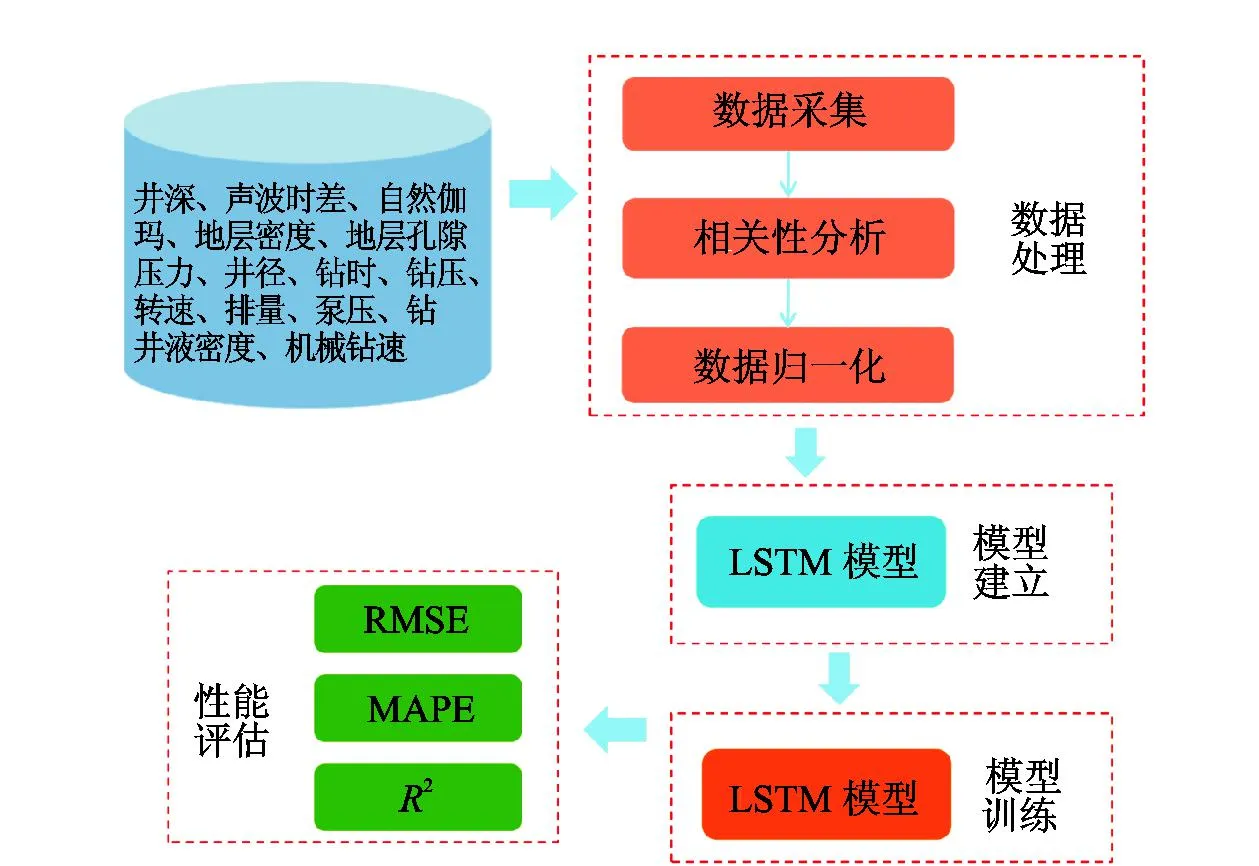
图1 机械钻速预测工作流程图
1.2 数据处理
1.2.1 数据采集
采集得到吐哈胜北区块已钻井段的测井数据和录井数据,共1 853组数据,如图2所示。测井数据(图2(a))包括井深(Dept)、声波时差(DT)、自然伽玛(GR)、地层密度(ZDEN)、地层孔隙压力(PP)、井径(CAL);录井数据(图2(b))包括钻时(Drilling Time)、钻压(WOB)、钻头转速(BRS)、排量(PD)、泵压(Pump Pressure)、钻井液密度(Drilling fluid density,DFD)、机械钻速(ROP)。这些参数的统计信息见表1。
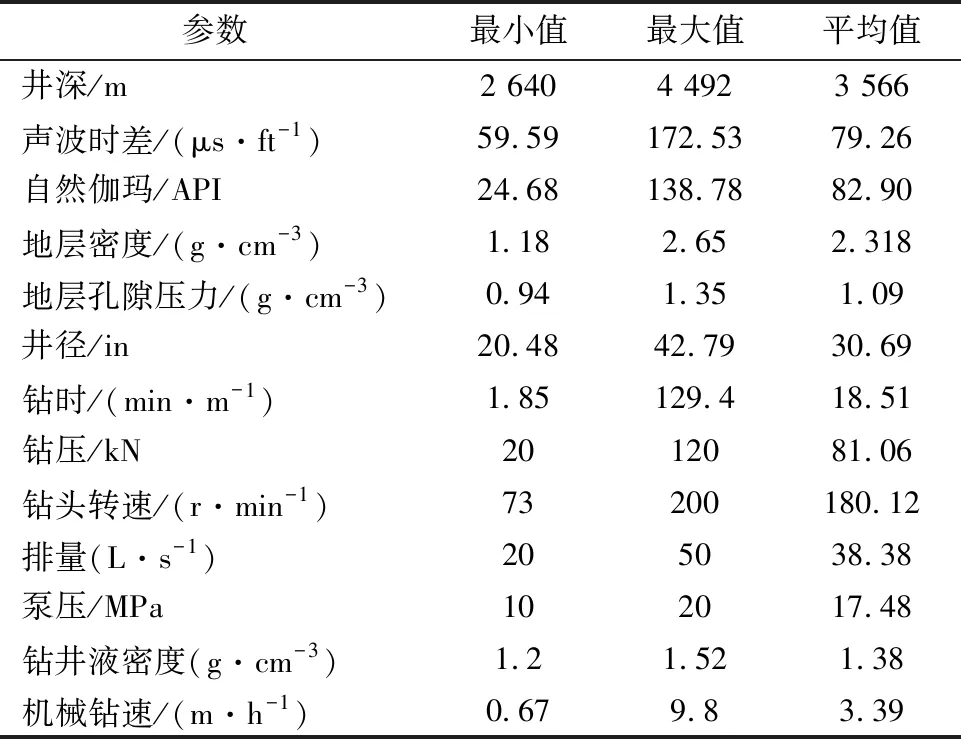
表1 原始采集参数统计信息表
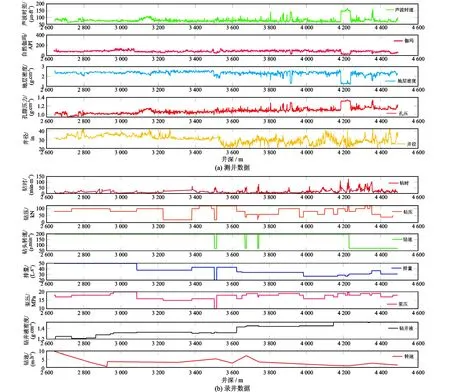
图2 原始采集数据
1.2.2 相关性分析与数据归一化
以往对机械钻速预测相关参数的选择是随意的,这些参数对钻速的影响有差异,而数据之间的相关性会影响模型训练速度和训练效果,在模型训练前需要对输入参数进行相关性分析,然后筛选出相关性较强的参数。采用皮尔逊相关系数[23]衡量各参数之间的相关性,则X和Y变量之间的皮尔逊相关系数表达式为
(1)
式中:r为相关系数,取值范围为[-1,1],值为正表示两特征呈正相关,值为负表示两特征呈负相关。
各参数之间的相关性热力图如图3所示。图3中,颜色越深则正、负相关性越强。选取与机械钻速相关性较强的井深、自然伽玛、地层密度、地层孔隙压力、井径、钻时、排量、钻井液密度这8个参数作为模型的输入变量。
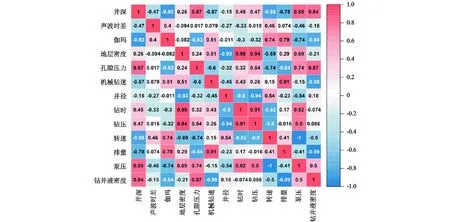
图3 各特征之间相关性热力图
数据归一化使每个维度的数据分布相似,可以避免不一致的梯度下降问题,有利于调整学习率,从而加快最优解的搜索[24]。按照
(2)
对经过相关性分析筛选后的输入参数进行最大最小归一化处理。式中:xi为输入数据;xmin为数据中的最小值;xmax为最大值;yi为归一化处理后的数据,取值范围为(0,1)。
2 模型搭建
2.1 LSTM网络结构与算法
LSTM神经网络是Hochreiter和Schmidhuber[25]于1997年首次提出,它是传统循环神经网络(Recurrent Neural Network,RNN)的一种优化算法,能够有效克服RNN的记忆暂存、梯度弥散等问题,且兼具长短期记忆功能,广泛应用于时间序列问题的预测[26]。深度序列和时间序列本质上是一样的,上一个数据点和下一个数据点之间存在内在的联系[27],因此可以用LSTM模型对深部地层机械钻速进行预测。LSTM网络结构如图4所示,左边是LSTM序列扩展逻辑架构图,可以沿横向(时间/深度)序列和纵向(层间)序列扩展,右边是单个LSTM内部逻辑关系图,主要包括遗忘门(ft)、输入门(it)、输出门(ot)和候选状态(ct0)。
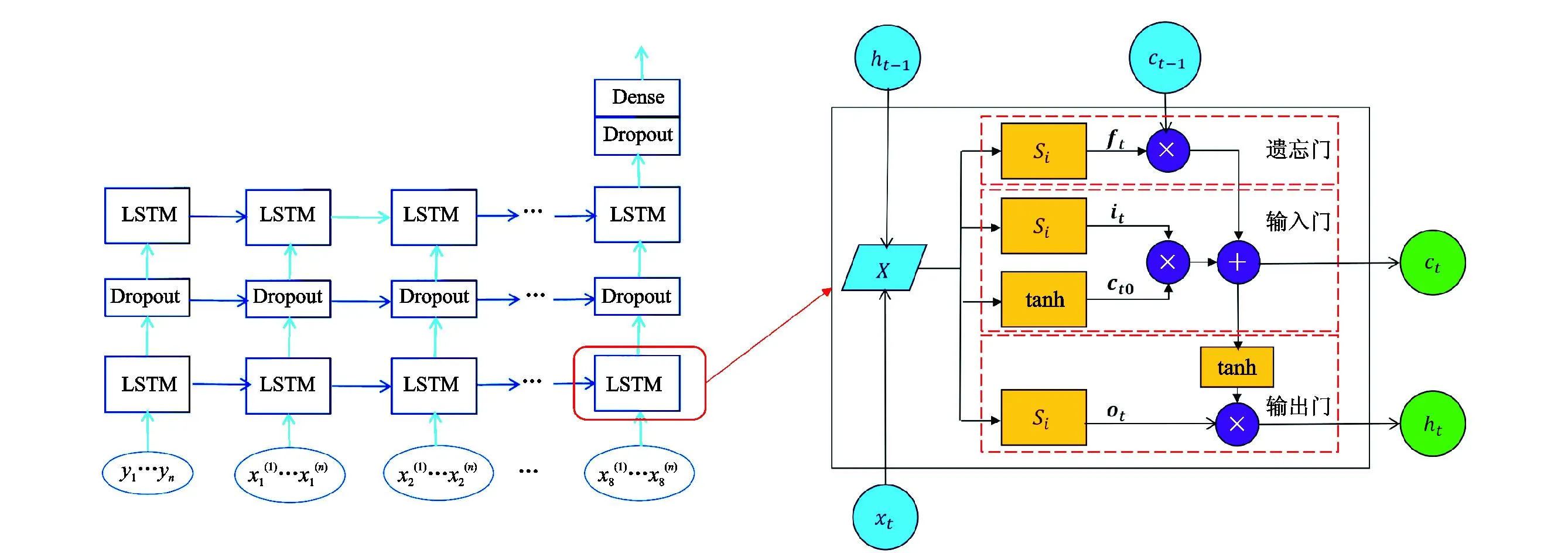
图4 LSTM神经网络逻辑结构
LSTM的权重矩阵和偏置项表达式分别为
W=[Wf,Wi,Wo]T
(3)
b=[bf,bi,bo]T
(4)
式中:W和b分别为LSTM的权重矩阵和偏置项,下标f、i、o分别表示遗忘门、输入门和输出门。
LSTM算法执行过程包括以下3步。
第1步经历遗忘门,它可以选择性忘记前一时间步的信息,该步骤由Sigmoid层实现,其表达式为
ft=sigmoid(Wf·[ht-1,xt]+bf),
(5)
(6)
式中:f为遗忘门;xt表示t时刻的输入向量;ht-1为t时刻的短期记忆;Sigmoid为激活函数,其输出范围为[0,1],0表示“完全忘记所有信息”,1表示“完全保留所有信息”。
第2步是输入门,它决定当前时间步存储哪些信息,该步骤由Sigmoid层和tanh层实现,即
it=sigmoid(Wi·[ht-1,xt]+bi),
(7)
ct0=tanh(Wc·X+bc),
(8)
(9)
式中:it为输入门;ct0为候选态;tanh为双正切激活函数,其输出范围为[-1,1];Sigmoid层决定更新信息,tanh层创建一个新候选值,将其添加到候选状态(式(8))。
经过上述步骤后,前一单元状态ct-1将更新为ct,即
ct=ct-1⊗ft+it⊗ct0。
(10)
式中:ct为更新后的长期记忆;⊗为逐点乘积。
第3步是输出门,它确定当前状态的输出。先运行Sigmoid层,得到输出单元,我们将单元状态放入tanh,将其乘以Sigmoid门的输出,这样只输出选择的部分,计算过程为
ot=sigmoid(Wo·[ht-1,xt]+bo),
(11)
ht=ot⊗tanh(ct)。
(12)
其中,ot为输出门;ht为当前单元状态的输出值。
ReLU也是常用的激活函数,其表达式为
(13)
经过LSTM各个门函数的更新,输入数据中的关键信息能够得到保留和传递,避免了梯度弥散问题,具备长期记忆功能。
2.2 LSTM神经网络层搭建
本文网络搭建和训练过程以及结果预测均在Matlab2021b进行,该版本带有深度学习工具包,选择深度网络设计器中序列到序列网络搭建LSTM神经网络层,该网络总与LSTM一起用于编码或解码和转换,LSTM神经网络层搭建过程主要包含输入层、LSTM层、节点层、网络分层和回归输出层5个步骤,需要在Matlab中对这5个步骤对应的函数变量值进行设置。
3 结果与讨论
3.1 训练过程和预测结果
对胜北区块的训练集在Matlab2021b中进行训练时,用均方误差作为损失函数,均方根误差(Root Mean Squared Error,RMSE)常用于衡量模型误差率,RMSE值越小,说明模型预测越精确[28],LSTM模型的训练过程如图5所示。由图5可知,模型可以收敛,且没有出现过拟合情况。LSTM模型的机械钻速预测结果如图6所示。图6表明模型的原始数据、测试数据和预测数据结果,蓝色曲线表示原始数据,绿色曲线为训练集预测结果,红色曲线表示后20 m步长的预测结果。
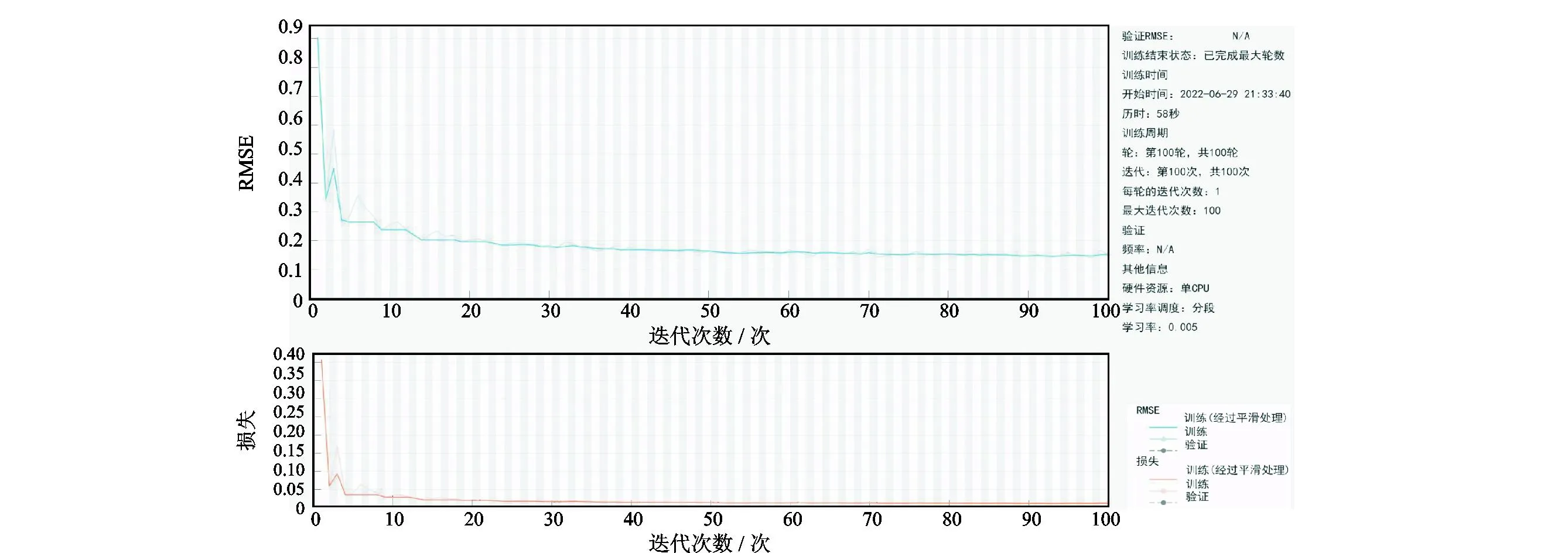
图5 LSTM模型训练过程损失曲线

图6 机械钻速预测结果
3.2 预测结果对比分析
本文对模型性能进行评价的指标是决定系数(Coefficient of Determination,R2)、RMSE、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),R2越大(接近1),RMSE越小,MAPE越小,表明模型预测效果越好[29]。优化前后模型性能评价指标见表2。
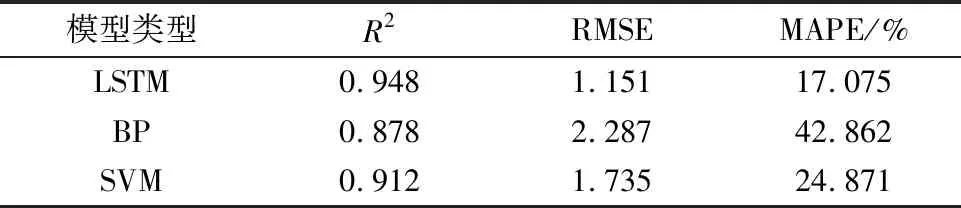
表2 模型性能评价指标对比
由表2可以看出,LSTM模型其R2、RMSE和MAPE的值分别为0.948、1.151和17.075,相较于BP模型和SVM模型,其R2更大,RMSE和MAPE较小,说明LSTM模型预测效果更好。
4 结 论
(1)提出将长短时记忆模型从时间序列应用到深度序列中,给钻井预测带来了新的思路。
(2)训练过程中模型可以收敛,且没有出现过拟合情况,可以用于预测机械钻速。
(3)LSTM模型R2、RMSE和MAPE的值分别为0.948、1.151和17.075,相较于BP模型和SVM模型,其R2更大,RMSE和MAPE较小,说明LSTM模型预测效果更好。
