基于标签多伯努利跟踪器的对手风险动态评估方法

王明阳 刘旭旭 李裕霖 李溯琪* 王佰录

①(西南电子技术研究所 成都 610036)

②(重庆大学微电子与通信工程学院 重庆 400044)

1 引言

在诸多的军事和民用领域都存在对手目标蓄意入侵我方重要区域从事恶意伤害活动的场景。典型例子包括计算机网络黑客入侵[1]、银行系统遭到恶意攻击以及军事战场敌我对抗[2]等。针对此类场景，依据场景中部署的传感器采集测量数据，评估和预测对手目标的一系列行动对我方资产造成的潜在伤害和损失[3,4]具有重要意义，评估资产的预期损伤，可有效地辅助我方下一步行动规划，提升重要资产和要害部位的生存率[5,6]。针对伤害或影响评估问题，国内外学者已开展相关研究，在不同场景下构建了多个期望伤害模型，白俄罗斯Tuzlukov[7]提出了风险转移模型，新西兰Bolderheij等人[8]提出运营风险模型，以及瑞典Johansson[9]则提出生存价值模型。然而，一方面，这些模型主要是离线评估的方法，难以实现对手目标动态变化过程中期望伤害的动态评估和预测，因此不适用于瞬息万变的博弈对抗场景。另外，还有一些学者，在军事战场场景下，针对优化我方资源配置问题，研究了武器库与攻击目标的最优匹配方法[9]。

近年来，英国利物浦大学Narykov等人[10]提出了对手风险(Adversarial Risk,AR)的概念，其定义是一组从事恶意伤害活动的对手目标对我方重要资产造成的期望伤害。相对于常见的伤害模型[8,11,12]，Narykov提出的对手风险模型更加完备，主要考虑了杀伤力无限和杀伤力有限两种情形。实际中，入侵的对手目标可造成的伤害具有不确定性。这种不确定性的一方面来源于成功打击与否的随机性，相应的打击概率受到目标与资产的几何位置关系、目标自身的杀伤范围、杀伤力等因素影响。另一方面，入侵的对手目标从远方来袭的过程中，目标数量、运动状态(位置、速度、加速度等)时变未知[13]，也是导致潜在伤害具有不确定性的重要原因。然而，对手风险模型仅建模了给定运动状态的多目标对于某高价值资产造成的期望伤害。因此，要实现目标动态变化过程中潜在伤害的在线评估，一种可行的方法是借助多目标跟踪器，先对多目标状态后验分布进行实时估计。

随机集统计理论(Finite Set Statistics,FISST)[14]的研究始于1994年。与传统向量统计理论不同，随机集理论将量测强不确定性和目标维度未知时变特性建模在点过程理论框架下，为多目标跟踪问题提供了统一最优贝叶斯滤波框架。随机集形式的多目标后验分布可同时描述目标数量、各目标状态的随机性以及目标间的统计相关性，特别适合于评估统计对手风险。借助随机集多目标跟踪器，迭代地计算每个时刻的多目标后验分布，进一步结合对手风险模型，即可对统计对手风险进行在线评估。针对任意随机集分布，文献[10]推导了对手风险的最优均方误差估计(及其方差)的表达式，但是涉及关于点过程强度函数和二阶统计矩的积分，无法直接实现。因此，结合Poisson点过程，文献[10]进一步给出了对手风险的最优均方误差估计(及其方差)的计算公式，并基于概率假设密度 (Probability Hypotheses Density,PHD) 跟踪器实现了对手风险的在线评估。

现有基于随机集理论的多目标跟踪算法主要分为两类，一类是非标签随机集跟踪器，包括伯努利(Bernoulli)跟踪器[15]、PHD[16]/基数均衡化概率假设密度(Cardinality Balanced Probability Hypotheses Density,CPHD)跟踪器[17]、多伯努利(Multi-Bernoulli,MB)跟踪器[18,19]等；另一类是标签随机集跟踪器，如广义标签多伯努利(Generalized Labeled Multi-Bernoulli,GLMB)跟踪器[20-22]，标签多伯努利(LMB) 跟踪器[23-30]等。与PHD滤波器相比，LMB跟踪器的优势体现在两个方面：(1)LMB跟踪器具备区别目标身份和建立目标航迹能力；(2)LMB跟踪器跟踪性能逼近最优贝叶斯跟踪器的闭合解GLMB跟踪器，尤其在低检测概率和高杂波率场景下，性能远优于PHD滤波器。

因此，本文在随机集理论框架下基于LMB跟踪器研究对手风险在线评估问题，主要贡献如下：

(1) 基于对手风险加性模型和乘性模型，分别推导了LMB分布的统计对手风险最小均方误差估计表达式。结合LMB跟踪器，提出了一种基于LMB跟踪器的统计对手风险在线评估方法。

(2) 对手风险最小均方误差估计涉及非线性函数的积分，因此没有闭合解。针对该问题，本文结合混合高斯近似和重要性抽样近似方法，提出一种对手风险最小均方误差估计的数值计算方法。

最后，模拟一组对手目标恶意入侵重要区域的场景，基于场景中监视雷达数据，验证了提出的对手风险评估方法的性能优势。

2 对手风险模型

对手风险[10,12]是指一组从事恶意伤害活动的对手目标对我方重要资产造成的期望伤害。对手风险大小可以由目标打击概率和目标杀伤力共同描述。以军事敌我对抗为例，目标的杀伤力一般指入侵的对手目标对于我方武器装备平台、重要港口城市、油田等重要资产的破坏程度。目标打击概率一般指对手目标成功打击我方重要资产的概率。

2.1节与2.2节根据对手目标杀伤力差异，建模了多目标对手风险加性模型、乘性模型；2.3节基于对手目标打击能力和打击意图，从两个维度精细化建立目标打击概率模型。

假设场景中存在n ∈N 个对手目标，其动力学状态由序列x1:n ∈Xn表示。依据对手目标对于资产的杀伤力强弱，可将多目标打击资产的方式划分成两类：(1)伤害叠加型；(2)一发击穿型。相应地，本节构建了两种类型的多目标对手风险模型。

2.1 加性模型

假设一组对手目标x1:n对我方资产A进行打击，其中，资产A的价值总值记为VA，目标xi对我方资产A的伤害值为dA(xi),i=1,2,...,n。若多对手目标x1:n对资产A造成的伤害即目标杀伤力较弱，不足以直接消灭我方资产，那么多个对手目标对资产造成的伤害可呈现叠加的形式，即资产受到总期望伤害为多目标期望伤害之和：

式(1)被称为加性对手风险模型[31-33]，用符号来表示，简称模型。

2.2 乘性模型

与2.1节类似，假设一组对手目标x1:n对我方资产进行打击，其中，目标i对我方资产A的伤害值为dA(xi),i=1,2,...,n。若目标xi对资产A造成伤害为∀dA(xi)≥VA,∀i=1,2,...,n即目标打击伤害能力较强，可以理解为对手目标能够一发击穿我方目标，则多目标中任意目标击中资产均可视为成功打击。相应地，多目标成功打击资产的概率可表示为[34]

因此，资产受到的总期望伤害可由式(3)计算：

2.3 打击概率模型

观察式(1)和式(3)，无论是加性模型还是乘性模型，成功打击概率τA(xi)都是对手风险的核心参数。本文主要考虑对手目标的典型特征包括打击能力和打击意图[35,36]，其中将打击能力建模为对手目标与我方资产的距离函数，而打击意图则与对手目标的打击角度具有强相关性。具体而言，建立打击概率的模型如下：

其中，cA(x):X→[0,1]表征对手目标打击能力，主要由入侵的对手目标与资产的几何位置关系决定，因此构建如下模型[37-39]：

其中，br表示对手目标潜在打击范围，r(x,xA):X×X→R+表示对手目标位置x与资产A位置xA之间的距离；iA:X→[0,1]表征目标的打击意图，主要由目标的速度方向决定，因此构建如下模型[40]：

其中，θ:X×X→[0,π]表示目标的打击角度，即目标速度方向和目标与资产连线的夹角，如图1所示，bθ为角度灵敏度参数。此外，建模目标打击概率还可考虑目标的速度、高度等更多维度信息[41,42]。

图1 对手目标打击我方资产场景示意图Fig.1 A schematic diagram of the scenario where the opponent’s targets attack own assets

3 基于LMB跟踪器的对手风险评估方法

基于LMB (Labeled Multi-Bernoulli)跟踪器的对手风险动态评估是根据场景中多个对手目标的实时观测数据，借助LMB跟踪器，序贯地对场景中任意位置(尤其是重要资产位置)的对手风险进行在线评估。

3.1 节构建了随机点过程下的统计对手风险模型，并基于最小均方误差原则在线评估对手风险；3.2节基于多目标对手风险模型，依据随机有限集(Random Finite Set,RFS) 多目标后验分布特征，推导对手风险分布最小均方误差估计的表达式，并提出基于重要性抽样的数值计算方法。

3.1 基于RFS的统计对手风险模型

在实际场景中，对手目标状态动态变化，且目标个数时变未知，因此多入侵目标的对手风险存在强不确定性，难以直接计算。基于有限集统计理论，可把数量和动力学状态未知时变的多目标建模为RFS(或随机点过程)的形式，同时为多目标跟踪问题提供了统一最优贝叶斯滤波框架。本节通过RFS建模多对手目标状态，构建基于RFS的统计对手风险模型，然后在最小均方误差准则下计算对手风险的最优估计。

首先，构造随机点过程Φ的统计对手风险如下：

其中，°表示函数合成运算算子，X={x1,x2,...,xn}表示多目标状态集合，n表示目标个数(随机变量)。

从数学上讲，统计对手风险RΦ(X)∈R 是随机点过程Φ的随机变量函数。若Φ的概率分布已知，则可利用概率论数学工具，分析RΦ(X)的统计特性。具体而言，RΦ(X)的一阶统计矩可表示为

其中，vΦ(x) 表示随机过程Φ的强度函数[14]。

其中，GΦ[·] 表示随机过程Φ的概率生成泛函(Probability-Generating Functionals,p.g.fl.s)[14]。

3.2 基于LMB分布的对手风险最小均方误差估计

在LMB跟踪器框架下，每时刻多目标后验分布是LMB分布的形式。结合加性模型和乘性模型，本节在式(9)和式(10)的基础上进一步推导LMB分布下对手风险最小均方误差估计的表达式。

3.2.1 加性模型

其中

将式(13)代入式(9)得

利用式(12)，LMB分布的对手风险最小均方误差估计可进一步化简为式(11)，定理得证。

3.2.2 乘性模型

定理2：给定k时刻LMB后验分布π(·|Z)=其中r(ℓ)和p(ℓ)(·|Z)由式(A-11)和式(A-12)给出。基于对手风险模型(式(3))，k时刻对手风险最小均方误差估计为

定理2证明：根据文献[10]，对手风险模型下，对于随机过程Φ，其对应的对手风险最小均方误差可表示为

由文献[14]可知，k时刻LMB后验分布的p.g.fl.s.可表示为

将式(17)代入式(16)，可得

进一步地，将LMB跟踪器后验参数r(ℓ)和p(ℓ)(x)的表达式(式(A-11)、式(A-12))代入式(18)，式(15)得证。

3.2.3 对手风险估计的数值计算方法

混合高斯近似方法是LMB滤波器最常见的实现方式[23]。本节基于混合高斯实现，进一步研究了对手风险估计的数值计算方法。假设LMB后验分布中参数p(θ)(·)是混合高斯的形式，即

(1) 加性模型

回顾2.3节中打击概率模型τA(x)(如式(4)所示)，显然cA(x)和iA(x)均为非线性函数，因此泛函F(θ)[dAτA]无解析解。为此，本文提出一种基于重要性抽样的数值计算方法。具体计算方法如下：

对于任意高斯分量j=1,2,...,J，进行NP的抽样，即

利用所获得的NP个样本近似计算F(θ)[dAτA]，可得

最后，将式(22)代入式(11)可得

(2) 乘性模型

然后将式(25)代入式(15)，可得

3.3 对手风险评估算法总体流程

图2给出了基于LMB跟踪器的对手风险评估算法的整体流程。如图2所示，提出的算法主要包含LMB跟踪器模块和对手风险评估模块，其中LMB跟踪器模块主要包含航迹预测和航迹更新；对手风险评估模块主要包含打击概率计算和对手风险的最小均方误差估计。

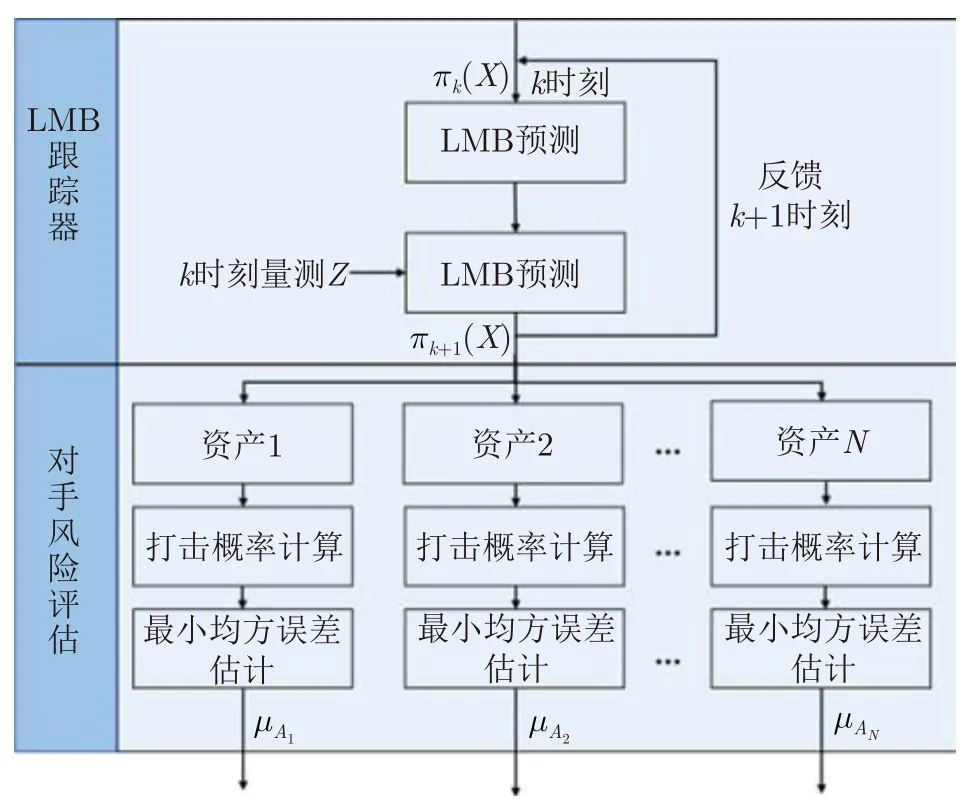
图2 对手风险评估算法整体流程图Fig.2 Overall flow chart of adversarial risk assessment algorithm

与基于PHD跟踪器的对手风险评估算法[10]相比，尤其在强杂波探测环境/低检测概率等复杂场景下，基于LMB跟踪器的对手风险评估结果更加准确且鲁棒性更强。

4 算法性能评估

本节模拟敌方目标突防攻击我方雷达阵地的场景，设计仿真实验，对基于LMB跟踪器的对手风险(AR)评估算法(简称LMB-AR算法)进行性能评估。算法性能评估以基于PHD跟踪器的对手风险评估算法(简称PHD-AR算法)作为性能标杆。

考虑低空监视雷达工作场景，观测总时间360 s。雷达坐标监视区域范围[-35,35]×[0,100]×[0,7]km，数据周期T=1 s。场景包含5个运动目标，运动轨迹如图3所示，各目标参数由表1给出。

表1 不同目标的出生时刻和死亡时刻Tab.1 The birth and death moments of different targets

图3 雷达监视场景-3D视图多目标真实运动轨迹Fig.3 Radar surveillance scene-3D view multi-target real movement trajectory

资产位置设置如下：资产S1位置(x1,y1,z1)=(-28050,0,0)m，资产S2位置(x2,y2,z2)=(9500,5500,45)m，资产S3位置 (x3,y3,z3)=(23900,3000,35)m。目标伤害值假设恒定，即dA=100，潜在打击范围br=15000 m，角度灵敏参数bθ=50°。

单目标状态转移模型假设为线性高斯模型，

其中，转移矩阵F和过程噪声强度协方差矩阵Q分别为

其中，

0n和 0m×n分别表示n×n维度和m×n维度的零矩阵；σν=5 m/s2表示过程噪声标准差。

考虑雷达量测zk=[r φ φ]T，其中r,φ,φ分别表示目标位置的径向距离、方位角、俯仰角，则单目标似然函数为非线性高斯模型：

其中，量测函数H(·)和量测噪声协方差矩阵R分别为

这里σr=30 m,σφ=0.5°,σφ=0.5°分别表示斜距、方位角和俯仰角的标准差；arctan(·)表示反正切函数。目标继续生存概率PS=0.98，每个目标的检测概率为PD，杂波分布是参数为λc的泊松过程。

PHD和LMB滤波器均采用混合高斯(GM)实现方法。各算法GM实现的参数选择如下：伯努利分量的截断门限为γt=10-4；GM实现的高斯分量截断门限与合并门限分别为γp=10-5和γm=4；高斯分量的最大个数限制为Nmax=10。对手风险评估的数值近似方法中，粒子数NP取10。

采用RMSE进行对手风险估计误差评估，所有统计性能结果均是100次蒙特卡罗(Monte Carlo,MC)实验的平均结果。真实对手风险计算方法为：将真实目标状态分别代入式(1)和式(3)得到真实的对手风险R，利用评估算法计算第n次实验的对手风险估计值则对手风险的RMSE计算如下

其中，N表示总实验次数。

4.1 单次实验结果

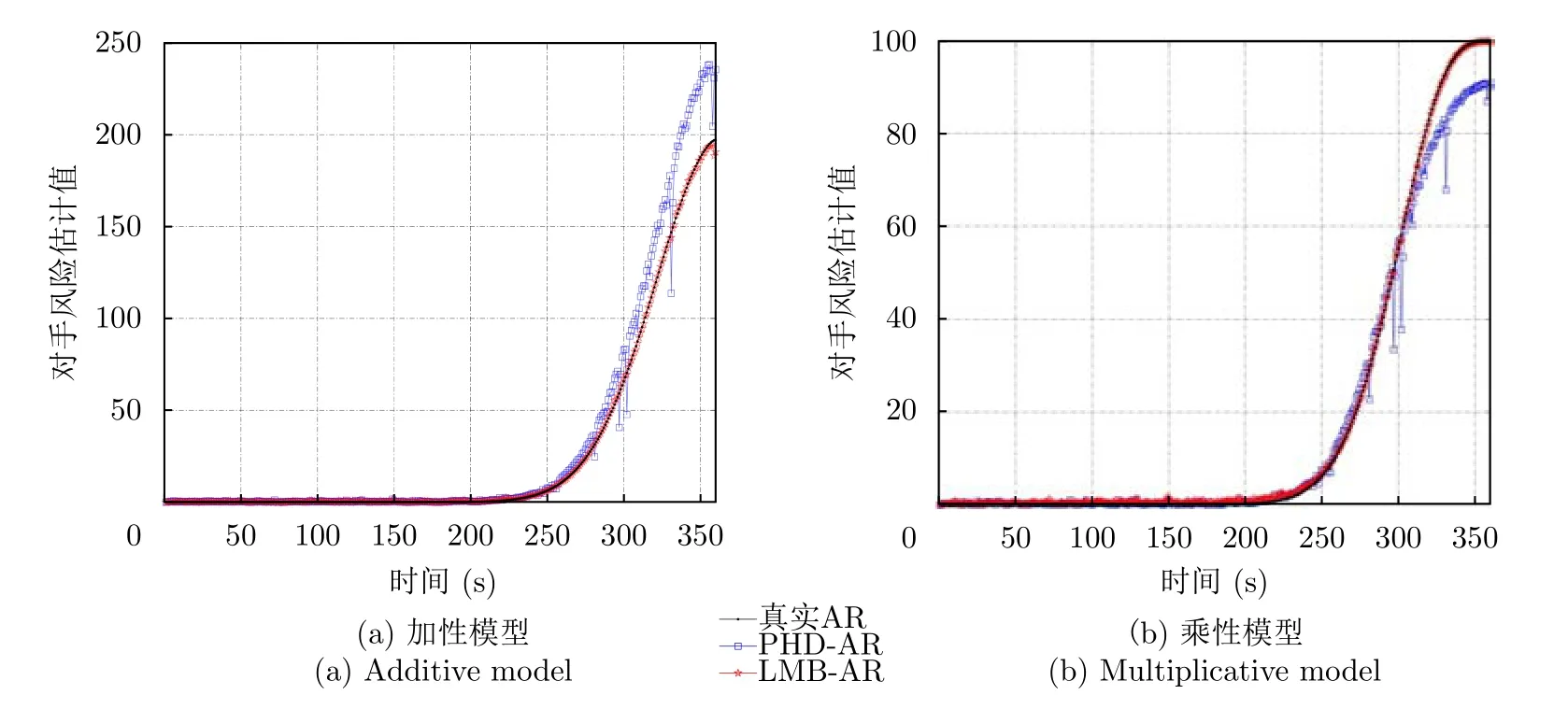
图4 杂波率 λc=25，检测概率 PD=0.8下，资产1的PHD-AR算法和LMB-AR算法的对手风险估计值随时间变化的曲线Fig.4 Curves of the counterparty risk estimates of asset 1’s PHD-AR algorithm and LMB-AR algorithm changing over time under the clutter rate λc=25 and detection probabilityPD=0.8

图5 LMB-AR算法的全场景对手风险估计热力图Fig.5 Heat map of full-scenario opponent risk estimation of LMB-AR algorithm

图4(a)，图4(b)表明，加性模型下目标对手风险呈叠加型，乘性模型下目标的对手风险峰值与资产的价值相当，验证了算法的有效性。且与PHD-AR评估算法相比，本文所提出的LMB-AR评估算法，更加接近真实的对手风险评估结果。PHD-AR评估算法结果与真实结果的偏差随时间推移而增大。开始阶段，目标距离资产较远，对手风险小，差异不明显。目标靠近时，对资产威胁增大，对手风险增加，差异变得显著。而文本所提出的LMB-AR评估算法并未出现上述情况，在对手风险较大阶段，LMBAR评估算法仍能得到较好的评估结果。此外，从图4(a)，图4(b)中可以看出，在某些时刻，PHDAR算法输出的对手风险评估结果急剧下降，评估结果出现跳变，该结果是由PHD跟踪器漏跟造成的。另一方面，LMB-AR评估算法输出结果在整个时间段内连续稳定且紧跟真实的对手风险评估结果。

图5(a)，图5(b)表明LMB-AR算法在实时估计全场景的对手风险时同样有效，可以实时反映战场态势，具有重要意义。

4.2 性能评估

实验1：相同杂波率，不同检测概率下算法性能比对。

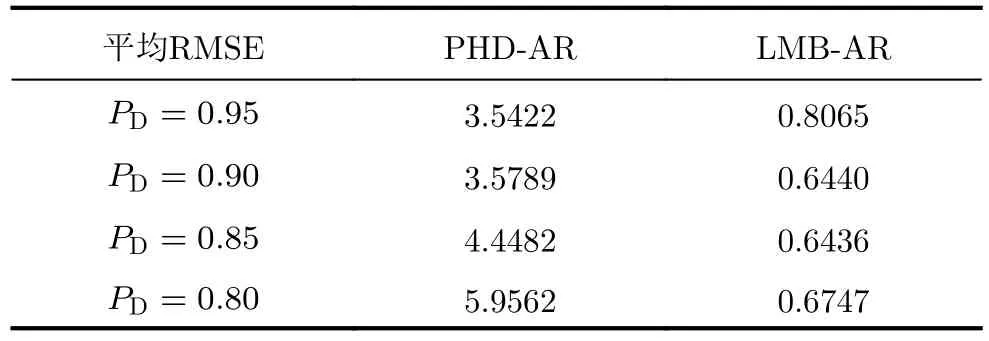
表2 杂波率 λc=25，不同检测概率下，加性模型PHD-AR算法和LMB-AR算法资产1对手风险估值的平均RMSE比较Tab.2 Comparison of average RMSE of asset 1 counterparty risk valuation of additive model PHD-AR algorithm and LMBAR algorithm under fixed clutter rate λc=25 and different detection probabilities

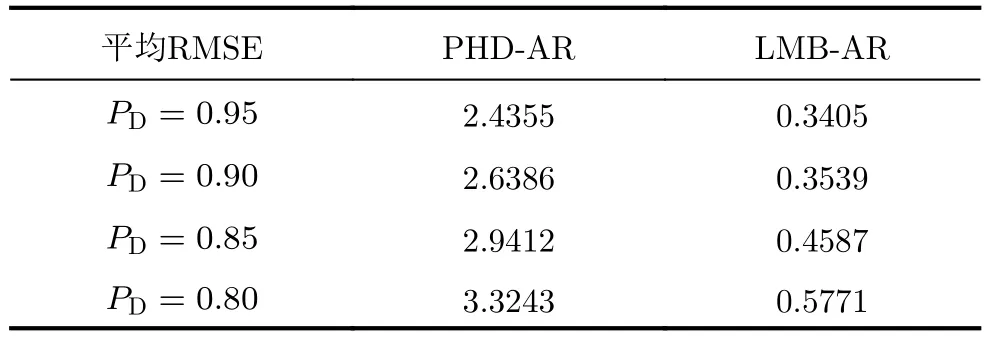
表3 杂波率 λc=25，不同检测概率下，乘性模型PHD-AR算法和LMB-AR算法资产1对手风险估值的平均RMSE比较Tab.3 Comparison of average RMSE of asset 1 counterparty risk valuation of multiplicative model PHD-AR algorithm and LMB-AR algorithm under fixed clutter rate λc=25 and different detection probabilities

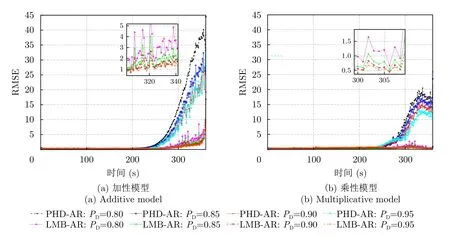
图6 固定杂波率 λc=25，不同检测概率下，资产1的PHD-AR和LMB-AR的对手风险估计RMSE随时间变化的曲线Fig.6 Curve of counterparty risk estimate RMSE of asset 1’s PHD-AR and LMB-AR changing over time under fixed clutter rate λc=25 and different detection probabilities

实验2：相同检测概率，不同杂波率下算法性能比对。

表4 检测概率 PD=0.90，不同杂波率下，加性模型PHD-AR算法和LMB-AR算法资产1对手风险估值的平均RMSE比较Tab.4 Comparison of average RMSE of asset 1 counterparty risk valuation of additive model PHD-AR algorithm and LMB-AR algorithm under detection probabilityPD=0.90 and different clutter rates

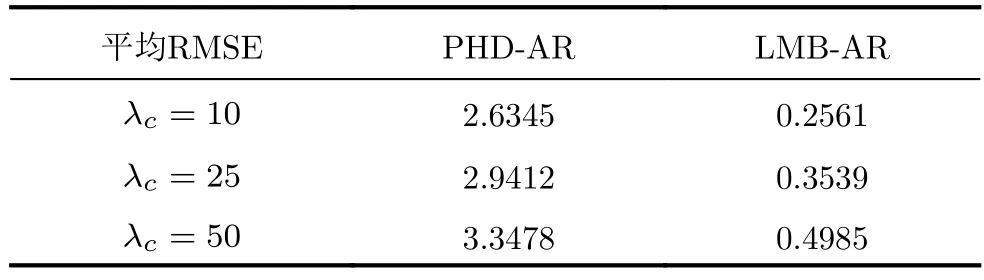
表5 检测概率 PD=0.90，不同杂波率下，乘性模型PHD-AR算法和LMB-AR算法资产1对手风险估值的平均RMSE比较Tab.5 Comparison of average RMSE of asset 1 counterparty risk valuation of multiplicative model PHD-AR algorithm and LMB-AR algorithm under detection probability PD=0.90 and different clutter rates

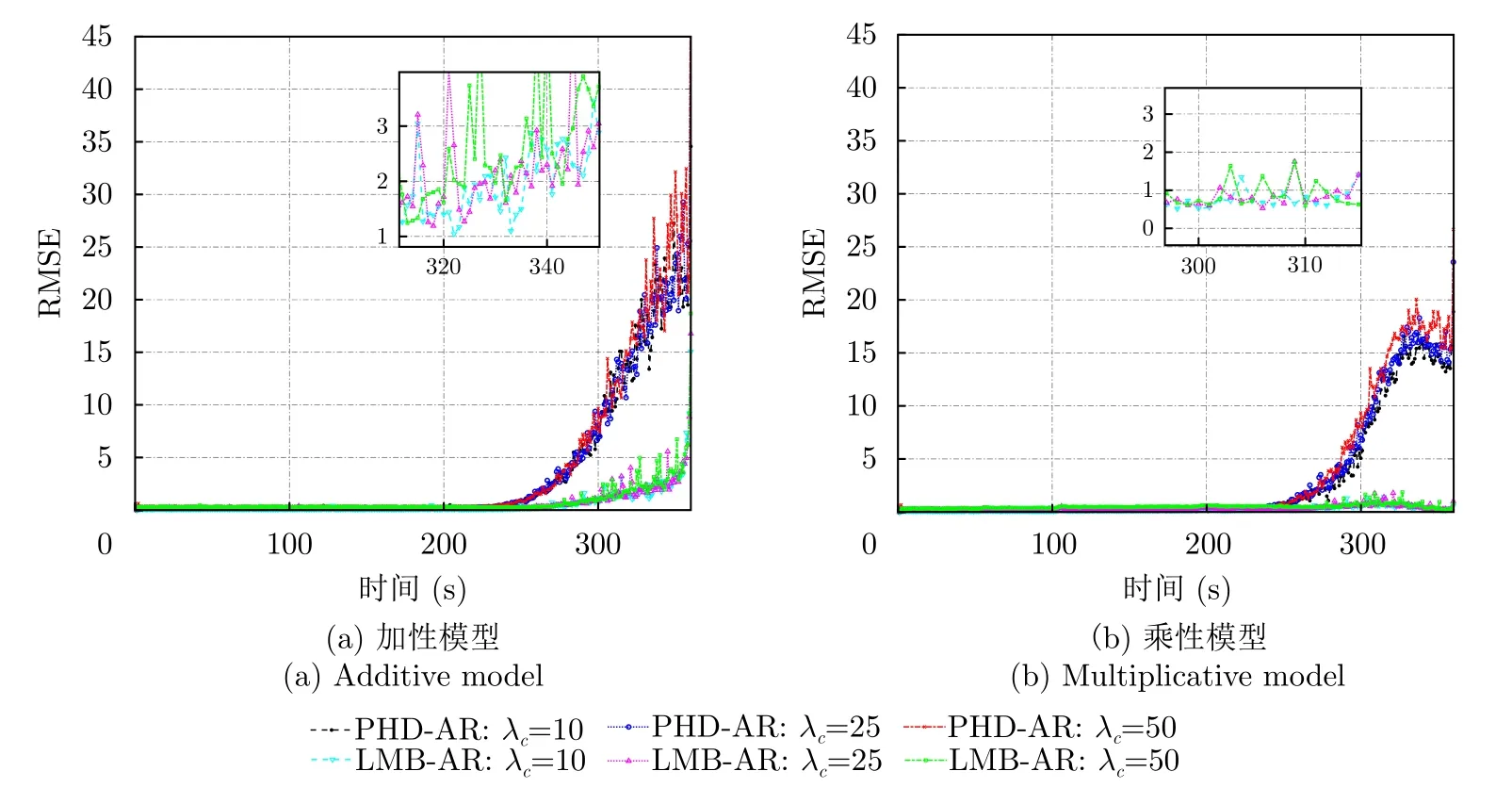
图7 检测概率 PD=0.90，不同杂波率下，资产1的PHD-AR和LMB-AR的对手风险估计RMSE随时间变化的曲线Fig.7 Curve of the counterparty risk estimate RMSE of asset 1’s PHD-AR and LMB-AR changing over time under detection probability PD=0.90 and different clutter rates

结果分析：LMB-AR算法相较于PHD-AR算法无论是单次实验结果或是平均RMSE结果均有较大的性能提升。该得益主要源于两个方面：

(1) LMB分布的自由度更高，统计风险模型更准确。PHD-AR算法中，多目标状态的统计特性是由Poisson过程描述的，假设目标数目服从Poisson分布且多目标独立同分布，假设较局限。而LMB-AR算法中，多目标状态后验服从LMB分布，目标数量分布的自由度更高，且放松了多目标独立分布的假设。

(2) LMB滤波器性能更优。相比于PHD滤波器，多目标状态估计更加准确，因此相应地，统计对手风险作为多目标状态的随机变量函数，其统计矩(最小均方误差估计)更加准确。

5 结语

在诸多军事和民用领域都涉及对手目标试图入侵我方重要区域从事恶意伤害活动的场景，而评估入侵目标对我方重要资产的期望伤害具有重要的实际意义。本文在随机集理论框架下基于标签多伯努利(LMB)跟踪器研究对手风险在线评估方法。首先，在LMB跟踪器的框架下，基于加性伤害模型和乘性伤害模型，分别推导了统计对手风险最小均方误差(Minimum Mean Squared Error,MMSE)估计的表达式。其次，针对所涉及的非线性函数积分问题，结合混合高斯近似和抽样近似方法，提出统计对手风险最小均方误差估计的数值计算方法；最后，将统计对手风险评估方法与LMB跟踪器的迭代过程有机结合，可实现入侵多目标对我方重要资产期望损失的动态在线评估。模拟多个具有杀伤能力的目标攻击雷达阵地的场景，利用雷达获取的实时点迹量测数据，验证了提出算法的有效性和性能优势。

附录 LMB跟踪器

LMB跟踪器是一种具有较高跟踪质量的随机集跟踪器，其跟踪性能逼近最优贝叶斯跟踪器的闭合解GLMB跟踪器，尤其在低检测概率和高杂波率场景下，性能远优于PHD跟踪器等其他随机集滤波器。

(1) 标签随机集和LMB分布

令 X 和 L分别表示目标状态空间和(离散)标签空间。X表示定义在增广空间 X×L上的随机有限集。令L:X×L→L 表示投影L((x,ℓ))=ℓ，则L(X)={L(x),x ∈X}表示多目标状态X的标签集合。若X与其标签集合L(X) 具有相同的基数，即|L(X)|=|X|，则称X为标签随机集。约束条件|L(X)|=|X|保证了标签随机集中各目标身份的唯一性。

LMB随机集是一种典型的标签随机集，服从如下分布：

其中，

Δ(X)≜δ|X|(|L(X)|)表示互异标签指示器；为多目标指数符号；r(ℓ)表示目标ℓ的存在概率；p(·,ℓ) 表示目标ℓ存在条件下的概率密度；1Y(X)为指示函数，其定义如下：

则LMB分布可由LMB参数集合完全表征。

(2) LMB跟踪器迭代递归方程

LMB跟踪器在性能上逼近最优贝叶斯跟踪器的闭合解GLMB跟踪器，同时在计算复杂度上远小于GLMB跟踪器。LMB跟踪器中，假设多目标后验密度服从LMB分布，通过贝叶斯预测和贝叶斯更新两个步骤，对每个时刻多目标后验分布进行迭代计算。LMB跟踪器的迭代递归方程具体描述如下：

(a) 预测方程：假定k-1时刻多目标后验密度为LMB分布，其参数集为π=k时刻新生目标同样服从LMB分布，其参数集为则k时刻多目标预测概率密度函数为

其中

这里L+L∪B;pS(·,ℓ)表 示k时刻目标ℓ的存活概率；f(x|·,ℓ)表示目标ℓ的状态转移函数。

(b) 更新方程：假定k时刻多目标预测密度函数为式(A-5)所示的LMB分布，传感器接收到量测集合Z，则多目标后验密度可近似为一阶矩匹配的LMB分布，其参数化表征为ℓ ∈L+}，其中

其中，pD(x,ℓ) 表示目标ℓ的检测概率；定义θ:L →{0:|Z|}{0,1,...,|Z|}为目标航迹-量测的关联映射；ΘI+表示标签集合I+与量测Z的关联映射空间，包含所有关联假设θ。

利益冲突所有作者均声明不存在利益冲突

Conflict of InterestsThe authors declare that there is no conflict of interests