基于稀疏恢复的雷达信号处理研究综述
2024-01-21全英汇吴耀君段丽宁刘智星邢孟道
全英汇 吴耀君 段丽宁 徐 刚 薛 敏 刘智星 邢孟道
①(西安电子科技大学电子工程学院 西安 710071)
②(西安市先进遥感重点实验室 西安 710071)
③(东南大学信息科学与工程学院毫米波全国重点实验室 南京 210096)
④(西安电子科技大学前沿交叉研究院 西安 710071)
1 引言
当信号通过某些特征空间进行表示时,只有很少部分系数非零,且非零元素的个数远远小于信号的长度,此时可以认为信号在该特征空间中是稀疏的,将稀疏性的先验信息引入到信号处理过程可有效解决传统信号处理技术无法解决的技术难题。基于稀疏性的信号处理中,先验稀疏性以信号处理的约束条件形式存在,基于稀疏性约束进行信号处理的历史由来已久[1],在20世纪稀疏信号处理技术就已被应用于图像处理等领域,但是整体而言稀疏信号处理处于较为缓慢的发展阶段。2006年,著名的压缩感知模型被提出[2],Candès从数学角度对该理论的一些关键问题开展了研究,极大推动了压缩感知理论的发展与完善。压缩感知理论突破了传统的采样定理,可从远小于传统理论所需的采样值中恢复出原始信号。该理论的基本条件是信号稀疏,通常采用范数对稀疏信号的稀疏度进行度量,ℓ0范数优化为恢复稀疏信号提供了有力工具,但是该问题难以求解。Donoho等人[3]研究了最小ℓ0范数解的唯一性问题,证明了最小ℓ1范数解与最小ℓ0范数解的等效性,推动了ℓ1范数重构算法的发展。之后出现了如迭代阈值类算法、梯度投影重构算法以及最小绝对收缩和选择算法(Least Absolute Shrinkage and Selection Operator,LASSO)等的求解方法。Mallat等人[4]首次将匹配追踪算法应用到了信号稀疏分解任务,之后大量学者开展了如正交匹配追踪等算法的研究;稀疏贝叶斯学习算法也被应用于求稀疏解。2010年,Gregor等人[5]设计了算法深度展开框架,从该工作中衍生出的模型驱动自学习思想为高效稀疏恢复算法提供了新的思路[6]。针对网格失配问题,也涌现出了基于动态词典[7]与无网格压缩感知模型的稀疏恢复方法[8]。
伴随着压缩感知的模型[9-11]、求解算法[12-14]与性能边界分析[15-17]等相关理论的逐步完善,基于压缩感知的稀疏信号处理技术在雷达探测[18]、阵列信号处理[19,20]、图像处理、遥感成像[21-23]、无线通信[24-26]等领域广泛应用,由于现代雷达探测场景的目标稀疏特性,稀疏信号处理在雷达中的应用更是获得了广泛而迅猛的发展[27-29]。2007年,Baraniuk等人[18]首次正式讨论了压缩感知原理在雷达成像中的应用,证明了压缩感知应用于雷达成像的可行性。2009年,Herman等人[30,31]对基于压缩感知的距离-多普勒雷达的目标高分辨展开研究。Mishali等人[32]在2010年较为系统地提出了一种基于压缩感知理论的宽带稀疏信号采集系统。Ender等人[33]较为系统地探讨了压缩感知理论在雷达系统中的脉冲压缩、雷达成像、波达方向估计等方面的应用。Yu等人[34]对压缩感知理论在多输入多输出雷达系统的应用展开了研究。
稀疏信号处理技术在雷达信号处理中的作用可分为两个方面。一方面,稀疏信号处理被用于解决传统体制雷达信号处理中的固有问题,以提升雷达目标探测性能、抗干扰性能以及雷达成像性能等[31,35-39]。另一方面,随着雷达目标特性测量、抗干扰等需求的不断发展,雷达的探测任务日益复杂化,硬件性能约束下的多任务雷达体制也日新月异,催生了比如频域稀疏雷达、稀疏阵列雷达等新型雷达体制,与传统体制雷达相比,此类雷达往往具备低成本、轻量化、体积小、抗干扰性能强等系统级优势,但是此类新体制雷达却使得传统信号处理方法不再适用,为此相关学者将压缩感知模型引入新体制雷达的信号处理中,来完成此雷达的波束形成[40-42]、目标参数估计[43-45]与成像[46-48]等。现代雷达的典型数字信号处理流程为空域处理、脉冲压缩、相参处理以及目标检测。稀疏信号处理作为一种通用信号处理方法,被广泛应用于不同体制雷达的各个信号处理环节。
2 压缩感知理论模型
随着数字信号处理技术的快速发展,如何从庞大的数据中稳定有效地提取出有用信息,剔除冗余信息,感知和挖掘信息内在结构和规律,是人们关注的重点问题。传统的奈奎斯特采样定理要求信号的采样频率必须大于信号带宽的两倍,才能完整地恢复原始信号,随着信号带宽的增大以及探测精度的提升,奈奎斯特采样框架对硬件采样带来了巨大压力,制约着信号的处理过程。为此,压缩感知[2,9-11,49-52]采样框架应运而生。压缩感知采样可以同时完成信号的压缩和采样、减小采样率、降低信号存储和传输压力,从而降低硬件成本,具有重要的理论意义和应用价值。
2.1 压缩感知模型
使用压缩感知方法的前提条件是信号是否具有稀疏性,若信号在某些基映射下可表示为稀疏形式,则称信号是稀疏的。
假设一个长度为N的离散信号x=[x(1),x(2),...,x(N)]∈CN可由一组变换基矩阵Ψ=[ψ1,ψ2,...,ψN]的线性组合表示为[2]
其中,Ψ为变换基;θ为基矩阵对应的N×1维的向量,包含K(K≪N)个非零元素,由投影系数θi组成,是离散信号x在变换基下的另一种表示方式。此时θ中的非零元素很少,且满足:
则可认为信号x在Ψ域下是K-稀疏的。其中‖·‖0为向量的ℓ0范数,‖θ‖0表示θ中非零元素的个数。但实际的信号中往往混杂着噪声,使得很难严格满足以上述稀疏性的条件,此时θ包含少量较大数值的系数,其余的系数较小,称这类信号为近似稀疏信号。
信号的稀疏性可以理解为信号在某个变换域下的分布特性,对同一信号,在不同的变换域中表示各有不同,不存在一个唯一的最佳稀疏变换基,选择何种变换基要根据实际信号特征来决定,由于变换基选取通常会决定稀疏恢复的效果,因此在基于压缩感知模型的雷达信号处理中,如何选择稀疏特征域对雷达回波进行稀疏表征,是建立雷达信号处理的压缩感知模型进而实现目标参数稳健估计的关键。
压缩观测作为压缩感知过程的另一关键环节,其与传统采样框架最大的不同是不对接收信号直接采样,而是先对信号做压缩处理。压缩观测通过观测矩阵将高维稀疏信号投影到低维空间上,保留信号的有效特征量。这样在采样过程中可以降低采样压力,仅对信号的有效信息进行采样。
压缩观测过程最重要步骤是构造观测矩阵,适合的观测矩阵可显著提升压缩感知理论的应用效果。本文用Φ∈CM×N来代表观测矩阵,通过其对长度为N的信号x进行压缩采样后,可以得到长度为M(M ≪N)的观测向量y,压缩观测过程可表示为
将式(1)代入式(3)可以得到:
其中,Θ=ΦΨ为M×N的矩阵,称为感知矩阵。式(4)未知量个数远远大于方程的个数,属于欠定问题,有无穷多组解。压缩感知理论通过给上述问题增加ℓ0范数约束,将通过少量线性观测恢复出原始稀疏信号的问题转化为
整个压缩观测过程如图1所示。

图1 压缩观测过程Fig.1 The process of compressing observations
压缩感知采样框架下的信号恢复是一个非线性约束问题,考虑到实际观测信号中会不可避免混杂噪声,在噪声条件下,信号重构可用ℓ0范数优化问题表示为
其中,ε的值由噪声能量决定。
若要精确的恢复信号,Θ需要满足一定的列正交性或者近似正交性[3,53-55]。针对矩阵相关性,有两种常用的衡量方式,一种是约束等距性条件(Restricted Isometry Property,RIP),一种是互不相干性(Mutual Incoherence Property,MIP),矩阵的MIP条件或者RIP条件为稀疏恢复算法提供了理论保证。Candès和Tao在文献[56]中提出使用RIP性质对矩阵的正交性进行度量,用数学表达式可写为
其中,δK是约束等容常数,值比较小,一般δK<1 ;θ为K-稀疏向量;当Θ使得式(7)对于任意满足ℓ0范数小于等于K的θ成立时,我们就称Θ满足稀疏度为K的RIP条件,则可以保证稀疏向量的稳健重构。
对于一个确定性的矩阵,矩阵的MIP特性通过最大相干系数进行衡量,Θ=[α0,α1,...,αn,...,αN-1],则最大相干系数定义为
其中,〈ai,aj〉为ai,aj内 积的模 值,‖ai‖2为ai的ℓ2范 数。当最大相干系数满足µ(Θ)<1/(2K-1)时[57],可对K-稀疏向量θ精确求解,该矩阵Θ具有MIP特性。压缩感知中,有多种对矩阵性质的度量指标,除了RIP,MIP性质之外,还有零空间性质(Null Space Property,NSP),L1-约束最小奇异值[53](L1-Constrained Minimal Singular Value,L1-CMSV)等多种性质。
传统的压缩感知理论中,稀疏信号的非零元素是随机分布的,但是在许多稀疏信号中,非零元素存在一定的结构,由此发展出如图稀疏结构[58]、块稀疏结构[59]、动态字典模型[7]、无网格模型[8]以及树状稀疏[60]等新模型。当信号中非零的元素成块出现时,称其为块稀疏信号,块稀疏的结构特性与雷达目标的特性具有很强的一致性,可以在雷达目标参数估计等应用中获得相较于传统算法更好的性能[61]。
2.2 优化重构
式(6)的求解是NP难(Non-Deterministic Polynomial-Time Hard)问题,实际中难以直接求解,目前对压缩感知模型的求解算法主要有凸松弛算法、贪婪追踪算法以及稀疏贝叶斯算法等。
(1) 凸松弛算法:此算法的本质是求解一个凸优化问题的最小值来重构稀疏信号。将ℓ0范数最小化的NP难问题转化为对ℓ1范数最小化的求解,将对非凸问题的求解转换为对凸优化问题的求解,来寻找全局最优解。典型算法包括:基追踪(Basis Pursuit,BP)[62]、迭代阈值(Iterative Thresholding)[63]等算法。该类算法估计能力较强,重构精度高,但是运算实时性较差,很难满足实际工程的需求。
(2) 贪婪追踪算法:该算法包括典型的如匹配追踪(Matching Pursuit,MP)[12]、正交匹配追踪(Orthogonal Matching Pursuit,OMP)[13]、正则化匹配追踪(Regularized OMP,ROMP)[14,64]和压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)[65]等算法,其基于ℓ0范数最小化策略,在每一次的循环迭代中利用最小二乘法对当前的残差向量进行更新,选择局部最优解,以此实现稀疏信号的重构。该类算法计算量较小,运算速度较快,但信号恢复精度较差。
(3) 稀疏贝叶斯算法(Sparse Bayesian Learning,SBL)[66,67]:该类算法将稀疏信号的重构问题转化为稀疏信号各元素的似然估计问题。首先根据信号的先验分布,采用贝叶斯理论进行概率计算,得到目标参数的后验分布,并对其进行参数估计。将稀疏贝叶斯算法应用到探地雷达成像领域中可降低数据存储量及数据采集成本,且在低信噪比(Signal to Noise Ratio,SNR)下成像效果更好[68]。
块稀疏是稀疏信号的特殊情形,经典的压缩感知重构算法可以对其进行处理,但是采用块CS重构算法,利用块稀疏信号的非零元素成块特点,可以获得相较于传统算法更好的性能[69]。典型的块稀疏恢复算法分为两类,分别是凸优化类算法以及贪婪追踪类算法。凸优化类算法如混合ℓ2/ℓ1范数优化算法,贪婪追踪类算法如由MP和OMP扩展来的块匹配追踪算法以及块正交匹配追踪算法[70]。
3 雷达回波信号的稀疏特性
当满足稀疏性的先验要求时[15],稀疏恢复技术可应用于传统体制雷达的信号处理;同时稀疏恢复技术也可应用于新体制雷达,用于解决传统信号处理方法不适用新雷达体制的问题。因此本节主要讨论传统体制雷达中的场景稀疏性与新体制雷达中的稀疏观测,为第4节的基于稀疏恢复的信号处理奠定基础。
3.1 场景稀疏
场景的稀疏性指的是雷达观测场景中的目标稀疏性,由目标的个数、尺寸、形状、材质等物理特性所决定,体现为雷达信号处理特征域下的稀疏。如在点目标探测中,目标的距离与速度只占据了有限个距离单元与多普勒单元;在雷达的高分辨一维距离像中,典型飞机目标的一维距离像只有有限个强散射点;在合成孔径雷达(Synthetic Aperture Radar,SAR)或者逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像中,目标呈现散射点分布,散射点个数远小于成像单元个数。下面结合窄带与宽带两种雷达体制依次讨论场景的稀疏性。
(1) 窄带雷达场景
目标个数的稀疏性是场景稀疏性的主要决定因素,在雷达观测场景中,受雷达威力以及波束宽度的限制,通常探测的目标数量小于雷达分辨单元个数,目标个数是稀疏的。但同时目标个数的稀疏性会和目标的特征域特征相结合,最终体现为信号处理特征域上的稀疏性,本文从时域、频域、空间域以及联合特征域对场景稀疏性进行分析。
(a) 时域稀疏
在时域稀疏性方面,回波信号经过脉冲压缩处理后,目标在粗分辨距离单元上呈现有限个强幅值响应点,强幅值点数远远小于整个快时间采样点数,具备时域上的稀疏性。
(b) 频域稀疏
在频域稀疏性方面,在雷达探测场景中,探测的目标个数稀疏时,对应分布在多普勒频率单元的强幅值点是稀疏的,频域具备稀疏性。
(c) 空间域稀疏
雷达探测场景中,目标仅占据少量的角度分辨单元,即目标在空域内是稀疏的。
(d) 距离-多普勒域
雷达探测场景中目标个数稀疏时,位于相同或不同距离单元的目标具备不同的多普勒,相应地,目标分布在距离-多普勒特征域的强幅值点是有限的,且强幅值点个数远小于距离-多普勒单元个数,目标在距离-多普勒单元上呈现稀疏分布[71]。
(2) 宽带雷达场景
根据雷达的分辨理论,雷达的距离分辨率与其带宽成反比,当雷达带宽足够大时,雷达距离分辨单元小于目标尺寸,目标不再由点目标模型表征,而是由更为复杂的散射特性进行描述。在SAR和ISAR等宽带高分辨雷达应用中,大带宽目标回波经过脉冲压缩处理,目标上各散射中心的回波将分布在不同的距离单元中,而目标的回波通常由几个强散射中心构成,强散射中心在成像平面上仅占很少的像素单元,具备稀疏性。
3.2 稀疏观测
雷达稀疏观测由雷达的体制、观测方式等决定,多体现为雷达系统设计或者雷达发射波形在各个特征域下的稀疏性,同时也会带来对探测场景的信息稀疏。比如稀疏阵列雷达的阵元分布为均匀布阵雷达的非完整采样,对目标在空域进行稀疏观测,具备空域稀疏性;频率捷变雷达发射的频率为工作带宽内的频率子集,对目标在频域稀疏观测,具备频域稀疏性。下面对典型的频域稀疏雷达与空域稀疏雷达进行讨论。
(1) 频域稀疏雷达
频域稀疏雷达是指雷达发射的波形中,频点具备稀疏性。雷达通过稀疏频率发射的方式提升电子对抗装备对雷达频点的分选识别难度。因而频率稀疏波形在雷达中得到了广泛应用,典型的频域稀疏雷达体制有频率捷变雷达、频率稀疏编码雷达以及稀疏捷变-正交频分复用(Sparse Frequency Agile Orthogonal Frequency Division Multiplexing,SFA-OFDM)雷达。
频率捷变雷达为雷达在相邻脉冲间进行载频随机/伪随机跳变的雷达体制。频率捷变雷达诞生于第二次世界大战期间,受限于当时电子器件的发展水平与信号处理水平,频率捷变雷达在诞生初期只能工作在非相参模式下[72],但随着电子技术的不断发展,频率捷变雷达逐步实现了全相参的工作能力。全相参频率捷变雷达的典型波形如图2所示[73],其中,f0为初始载波频率,Δf为跳频间隔,Tr为脉冲重复周期;雷达在相邻的脉冲间进行频率跳变,同时每个相参处理间隔内,雷达的有效频点为其工作总带宽的一个子集,即一个相参处理间隔内的信号载频具有频率稀疏性。

图2 频率捷变波形示意图Fig.2 Schematic diagram of frequency agile signal
频率稀疏编码雷达是指对单个脉冲内的信号划分子脉冲,对其进行稀疏频率编码。与脉间频率捷变雷达相似,频率编码波形也按照一定的随机/伪随机方式对频率序列进行设计,其典型的频率编码波形可以是频率步进波形、随机/伪随机步进波形以及稀疏编码波形等。典型的频率稀疏编码雷达波形如图3所示[74],其中,B为瞬时带宽,Tsub为子脉冲宽度,Tp为脉冲宽度,其编码序列为随机编码,通过设置脉内频率编码波形子脉冲频率间隔大于子脉冲带宽,雷达发射波形为频率稀疏编码信号。

图3 频率稀疏编码波形示意图Fig.3 Schematic diagram of frequency encoded modulated signal
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)波形是一种多载波同时发射的波形,最初应用于通信系统中。1998年,Jankiraman等人将OFDM技术引入到雷达系统[75]。之后,Lellouch等人[76]首次将捷变思想与OFDM技术相结合,提出了频率捷变-正交频分复用(Frequency Agile Orthogonal Frequency Division Multiplexing,FA-OFDM)信号,而SFA-OFDM是在FA-OFDM的基础之上发射稀疏子载波信号[77,78]。FA-OFDM波形示意图如图4(a)所示,在相参处理间隔的每个脉冲内发射多个频点随机跳变的子载波;如图4(b)所示为SFA-OFDM,其在一个脉冲内发射连续的一组子载波,但是不同脉间的子载波组频率稀疏,M为一个相干处理时间(Coherent Processing Interval,CPI)内的脉冲数,单个脉冲由K个带宽为Δf的子载波组成,N表示总的跳频数,N>M,脉间最小跳频间隔为B=KΔf,N个跳频信号的总带宽表示为Btotal=NB。

图4 波形示意图Fig.4 Schematic diagram of the waveform
(2) 空域稀疏雷达
空域稀疏雷达指的是雷达天线或者天线阵元的布阵方式存在稀疏性,雷达的天线布局设计以及雷达观测方式都会导致空域稀疏的现象发生,典型的空域稀疏可分为稀布阵与孔径稀疏两种。
在相控阵列或数字阵列中,广义的稀布阵指的是阵元非等间隔排布的阵列。在20世纪60年代至20世纪90年代,大量学者对稀布阵开展了研究[79-81],现代的稀布阵可以分为稀布阵列与稀疏阵列两种类别。两者的区别在于阵元排布方式以及阵元间隔的不同[82],稀布直线阵列阵元布局如图5所示[83],阵元数目为N,孔径大小为 |dN-d1|,d1,d2,...,dN分别表示阵元的不同坐标,θ表示从线阵开始扫描的角度大小。稀布阵列的阵元排布方式以及阵元间隔是任意的,只是受限于互耦效应以及阵元自身的尺寸等因素的影响,阵元间隔限制大于等于半波长,且阵元间距是互相不能整除的。

图5 稀布直线阵列的几何结构Fig.5 The geometry of the sparse linear array
稀疏直线阵列的阵元排布方式如图6所示[83],d为栅格间距,L=Md为孔径大小,孔径上有M+1个栅格点。稀疏阵列基于对均匀阵的采样而形成的非均匀阵列,通过阵元的稀疏排布,各阵元间距为栅格间距的整数倍。稀疏阵列可以减小阵元之间的互耦效应,可以在阵列孔径不减小的条件下,提高雷达分辨率[84]。
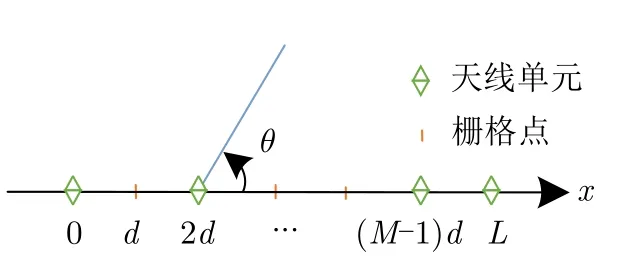
图6 稀疏直线阵列的几何结构Fig.6 The geometry of the thinned linear array
均匀直线阵列的阵元排布以及方向图如图7所示,图7(a)为均匀直线阵列的阵元排布方式,图7(b)为其相应的天线方向图,此时的阵元排布为等间隔的10个阵元。

图7 均匀直线阵列Fig.7 Uniform linear array
稀布直线阵列的阵元排布以及方向图如图8所示,阵元个数为8,图8(a)为稀布直线阵列的阵元排布方式,图8(b)为其相应的天线方向图,稀布直线阵列的阵元排布更具有随机性。

图8 稀布直线阵列Fig.8 Sparse linear array
稀疏直线阵列的阵元排布以及方向图如图9所示,阵元个数为8,是在均匀直线阵列的基础上对其进行采样,图9(a)为稀布直线阵列的阵元排布方式,图9(b)为其相应的天线方向图。
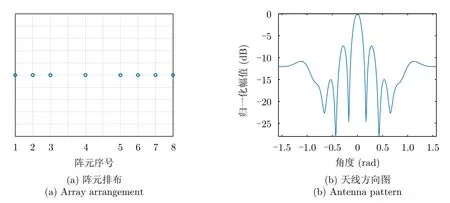
图9 稀疏直线阵列Fig.9 Thinned linear array
稀疏孔径是由于合成孔径雷达观测模式所带来的一种特殊的空域稀疏。合成孔径雷达通过对合成孔径时间内的信号联合处理,实现小孔径天线合成大孔径天线的效果,进而提升雷达的角度分辨率,但是随着雷达同时多任务的功能需求以及相控阵等灵活波束指向技术的应用,合成孔径雷达成像过程中雷达系统会分时执行不同的功能,从而导致对单一场景波束照射不连续或数据丢弃均会造成回波数据丢失,进而导致稀疏孔径[85]。
4 稀疏恢复在雷达信号处理中的应用
雷达观测场景中的先验稀疏性与雷达的稀疏观测方式为基于稀疏恢复的雷达信号处理提供了充分条件,本节结合传统非稀疏体制雷达与新体制雷达中不同信号处理需求,围绕空域处理、脉冲压缩、相参处理、雷达成像以及目标检测的典型雷达信号处理过程,对稀疏恢复技术在雷达信号处理中的应用展开讨论。
4.1 空域处理
压缩感知理论在空域处理的应用主要体现在空间谱估计、自适应波束形成以及阵列方向图综合等领域的应用。
在空域滤波应用方面,现有的方案主要是通过利用压缩感知和稀疏表示技术对阵列采样的相关矩阵进行更精确的估计,以此来提高和改善传统方法的目标参数检测性能[86]。针对传统的多重信号分类算法估计信源数与阵列形式之间的矛盾,文献[87]基于目标的空域稀疏性,采用OMP算法,在较少阵元数的条件下进行空间谱估计,并通过仿真进行验证。针对空域信号波达方向(Direction of Arrival,DOA)估计中采样数据量大以及受信噪比影响较大的问题,文献[88]提出了采用奇异值分解的多矢量欠定系统的聚焦求解算法,基于空域目标信号占据少量角度分辨单元的稀疏性,实现了DOA高分辨估计。文献[89]提出了一种基于深度展开交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)网络的离格DOA估计方法,可在提高估计精度的同时降低计算复杂度。针对空时自适应处理(Space-Time Adaptive Processing,STAP),利用稀疏恢复技术可以通过极少的样本估计杂波空时谱,有效降低STAP的运算复杂度。为了在小训练样本场景下提高杂波抑制性能,文献[90]基于稀疏约束投影近似子空间跟踪,提出了一种快速STAP算法。利用杂波协方差矩阵的低秩特性,在投影近似子空间跟踪的代价函数中施加稀疏约束,迭代推导出自适应权向量,与没有稀疏约束的传统STAP方法相比较,该方法具有更好的性能和更快的收敛速度。大多数基于稀疏恢复的空时自适应处理技术都受到角度多普勒平面离散化引起的离网效应的影响。空军预警学院王永良团队[91]提出了一种利用杂波脊先验信息划分非均匀网格的稀疏恢复-空时自适应处理(Sparse Recovery Space-Time Adaptive Processing,SR-STAP)方法,并证明了采用非均匀字典的SR-STAP算法后的杂波抑制性能优于传统的均匀字典。针对大规模字典应用,Cui等人[92]提出了一种基于张量的稀疏恢复空时自适应处理方案,传统的基于向量的运算被其相应的低复杂度张量表示取代,使得一个大规模的矩阵运算转化为多个小规模的矩阵计算,从而可以在恢复过程中节省巨大的运算量。
稀疏阵列由于阵元的稀疏性,通过少量阵元可以满足设计指标要求,同时降低成本。文献[93]提出了一种新的阵列稀疏方法,基于压缩感知理论求取稀疏线性阵列方向图,并验证了该方法在少量稀疏阵元实现低增益、强方向性的方向图效果的有效性。文献[94]构建了一个统一的空频域稀疏模型,可以同时估计载波和DOA,结合多传感器数据进行频谱重构,提高数据利用率和DOA估计精度,并通过频谱和DOA的时空分布特性解决了阵列参数估计中的源模糊和相干信号问题。同时根据信号空间分布的稀疏性特征,给出了一种空间分离处理方案,从而显著降低计算复杂度。另外,该方法放宽了对阵列流形的限制,适用于任意阵列,具有更广阔的应用前景,仿真和硬件结果验证了该方法的有效性。稀疏阵列的自由度可以利用无网格算法实现,可实现在避免网格划分的同时,恢复虚拟阵列空洞的响应[95]。文献[96]针对均匀/稀疏线性阵列的DOA估计问题,提出了一种基于协方差拟合准则的稀疏参数法,实现了在无网格的划分的同时实现DOA参数估计。
近年来,多任务贝叶斯压缩传感(MulTitask Bayesian Compressive Sensing,MT-BCS)已成功应用于单模式稀疏平面阵列的合成,在文献[97]中,Yu等人把MT-BCS扩展到多平面阵列方向图的合成,实现了在较短的时间内解决大规模阵列问题,并获得相对稀疏的结果。根据稀疏阵列场景信息,可构建如下模型[84]:
其中,X是阵列接收信号,S是空间目标角度位置,S中只有有限个元素是非零的,N是噪声,A表示场景感知矩阵,f(·)为场景关系函数。
杂波及干扰场景下,为提升空间角度超分辨性能通过对弱小目标角度位置进行加权来区分目标、噪声及干扰区域,则在目标角度求解过程中既能保证散射中心的恢复精度又能抑制噪声和干扰,结合稀疏表示与ℓ1,ℓ2分解方法,稀疏阵列角度超分辨压缩感知模型如下所示:
其中,W表示加权矩阵,gw(·)表示加权矩阵W与空间角度位置S之间的关系函数。利用稀疏信号处理技术对式(10)进行迭代求解,可获得空间角度超分辨结果。
基于上述的压缩感知模型,设置10×10阵面,50个阵元的稀布阵,空间角度分辨率为 11.5°,稀疏阵的排布如图10所示。在单快拍场景下,将初始角度分辨结果与OMP算法[4]进行比较,对比结果如表1及图11所示。图11(a)为初始角度分辨结果,图11(b)为通过OMP算法得到的空间角度超分辨结果。依据表1所示的误差分析结果以及图11所示的仿真结果对比,可以看出初始角度分辨结果分辨率较低,采用OMP算法可实现角度超分辨,但是存在一定的误差。

表1 计算结果对比图Tab.1 Comparison chart of calculation results

图10 阵面阵元位置分布Fig.10 Distribution of array element locations
4.2 脉冲压缩
基于匹配滤波理论,线性调频信号是应用最广泛的一种脉冲压缩信号。窄带雷达脉冲压缩处理中,通常利用匹配滤波实现。宽带雷达通常采用有源相关处理实现脉冲压缩,进而得到目标散射点的高分辨一维距离像。传统的脉冲压缩为了降低旁瓣需要进行加窗处理,但是加窗处理会存在主瓣展宽的现象[98,99];同时常规脉冲压缩的距离分辨率取决于信号的带宽,而基于目标场景的稀疏性,利用压缩感知可以实现对目标距离的高分辨。
相关学者开展了基于稀疏恢复思想实现脉冲压缩的研究,文献[37]针对大带宽信号传输数据量大的问题,结合SAR雷达系统的脉压工作机理,在降低距离像数据量的同时,基于脉压后距离上的强点稀疏性,运用压缩感知理论实现脉冲压缩;同时,与传统的匹配滤波方法进行对比,文献[37]表明压缩感知方法得到的脉压结果更加理想的旁瓣。文献[98]针对传统脉冲压缩低旁瓣与主瓣展宽的矛盾,提出了一种基于压缩感知的线性调频(Linear Frequency Modulation,LFM)脉冲压缩的实现方法,构造与脉压参考信号相关的稀疏基,利用平滑最小化0-范数算法,在保留回波信号的相位信息的同时对脉压结果实现了较高精度重构。文献[100]分别对匹配滤波以及去斜处理进行介绍,针对匹配滤波模式下的压缩感知距离压缩算法,通过对雷达作用距离范围进行网格划分,对发射信号进行延时构造稀疏基矩阵,将观测值以及重建矩阵代入重构算法,实现匹配滤波的脉压结果重构;针对去斜模式下的压缩感知距离压缩算法,稀疏矩阵为单位矩阵的傅里叶逆变换,稀疏恢复之后去除剩余相位,继而得到一维距离像。文献[101]针对宽带LFM信号的脉冲压缩处理,首先对其进行去斜处理,基于去斜回波信号的频谱稀疏性,采用正交匹配追踪算法重构了目标回波的一维高分辨距离像。假设雷达的发射信号为
Tp代表脉冲宽度,t代表快时间且满足 0<t<Tp,φ(t) 为脉冲内的信号调制,rect(·)表示矩形窗函数。
假设场景中有G个目标,τg表示第g个目标的延时,则混频后的雷达回波信号表示为
混频后对雷达回波数据采样得到s,K为稀疏基,H为量测矩阵,ζ为噪声项,ω为待求解脉压结果,则压缩感知模型可以表示为[98,99]
分别采用传统脉冲压缩算法以及正交匹配追踪算法对频率编码信号进行脉冲压缩。如图12所示,仿真场景中存在3个点目标时,目标形成的强幅值点在距离单元上呈现稀疏性,图12(a)为频率编码信号做传统脉冲压缩结果,可以看出此时的旁瓣较高,主旁瓣比为14 dB;采用正交匹配追踪算法实现脉冲压缩时,如图12(b)所示,此时脉压结果相较于传统方法旁瓣明显降低,但是相近的两个点目标之间存在一定的旁瓣。
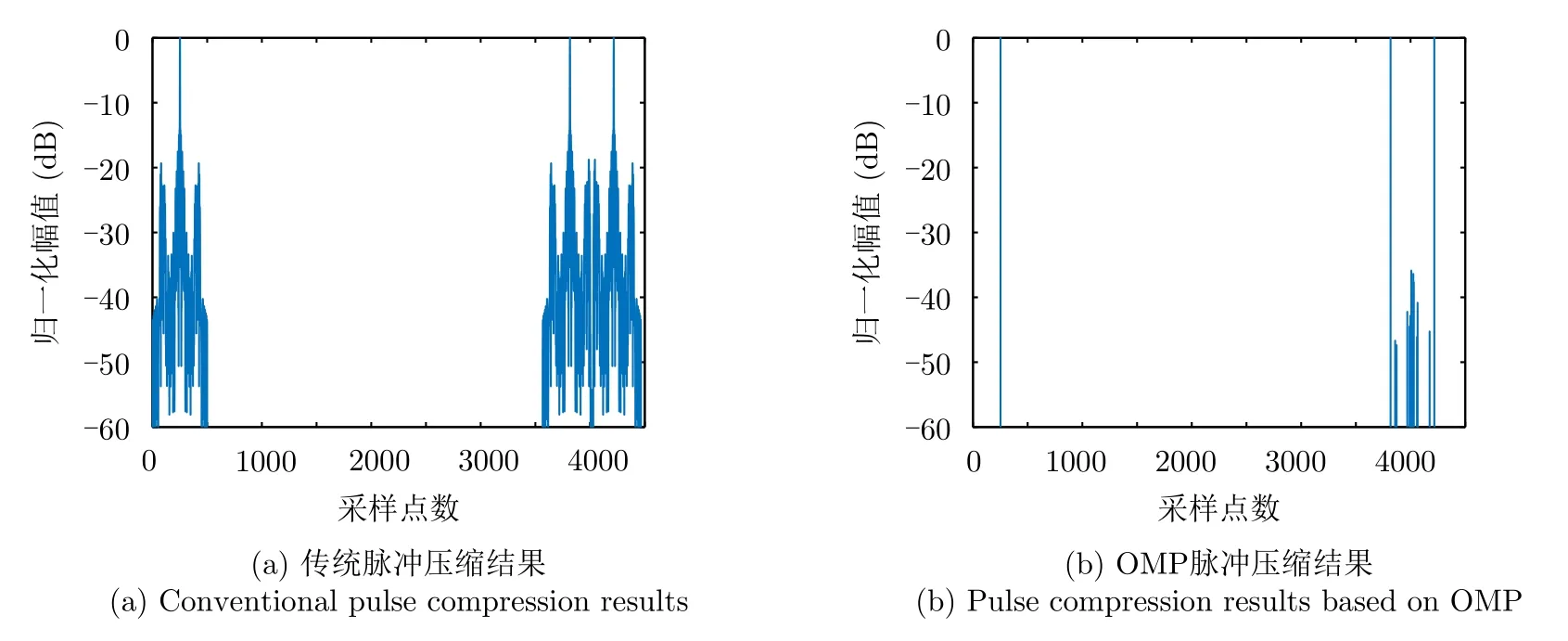
图12 传统算法与OMP算法的脉冲压缩结果Fig.12 Comparison of pulse compression results based on traditional algorithm and OMP algorithm
4.3 捷变相参处理
当雷达探测场景目标个数稀疏时,对目标回波进行脉冲压缩之后,一个粗分辨距离单元中往往只有有限个目标,因此一个粗分辨距离单元中的目标呈现出高分辨距离域、速度域或者距离-多普勒等联合特征域的稀疏分布,通过构造与目标特性相符的字典矩阵,利用压缩感知算法可实现对有限个目标的距离以及多普勒等信息的估计。
稀疏恢复在新体制雷达的相参处理方面的应用是稀疏信号处理的研究热点,被广泛应用于比如随机脉冲重复频率(Pulser Repetition Interval,PRI)抖动、脉间捷变、载频-重频联合捷变等雷达的相参处理中,由于重频抖动与频率捷变雷达可视作载频-重频联合捷变雷达的特例,假设雷达观测场景中存在G个目标,每个目标相对雷达的径向距离和径向速度分别表示为rg和vg,其中g ∈{1,2,...,G}为目标个数索引,Tq为慢时间序列,将第q个发射脉冲的载频为fq,fq=f0+d(q)Δf,其中 Δf为最小跳频间隔,f0为基准载频,d(q)是频率跳变编码,d(q)∈{1,2,...,N},N为总跳频点数,则第q个脉冲压缩后的载频-重频联合捷变回波信号表示为
其中,Tr代表平均脉冲重复频率,Tr/U(q)第q个脉冲的随机抖动程度。
根据探测场景稀疏性,构建压缩感知信号模型[102]:
其中,δ为噪声向量,S为对回波信号采样后做脉冲压缩处理的数据,Z为冗余字典矩阵,通过将雷达不模糊距离以及不模糊速度区间进行划分,使得字典矩阵中包含目标的距离以及速度信息,θ为待重构的相参结果。
基于场景稀疏性,利用字典矩阵和脉压数据可重建向量θ。然后,通过求解一个ℓ1范数最优问题对原始信号进行重构:
噪声项ε=‖δ‖2可以从相邻的距离/速度单元估计。
相对于固定参数脉冲多普勒(Pulse Doppler,PD)雷达而言,脉间捷变雷达的目标回波的脉间相位由线性变化转为非线性变化,如图13所示,图13(a)为PD雷达相位的脉间相位,图13(b)为脉间频率捷变雷达的脉间相位,可以看出脉间捷变雷达的相位在脉冲间非线性变化,这种变化使得传统动目标检测(Moving Target Detection,MTD)信号处理算法不再适用,基于场景的稀疏性先验信息,压缩感知技术被引入到捷变波形的相参处理中,实现了多脉冲联合处理并完成了目标的参数估计。
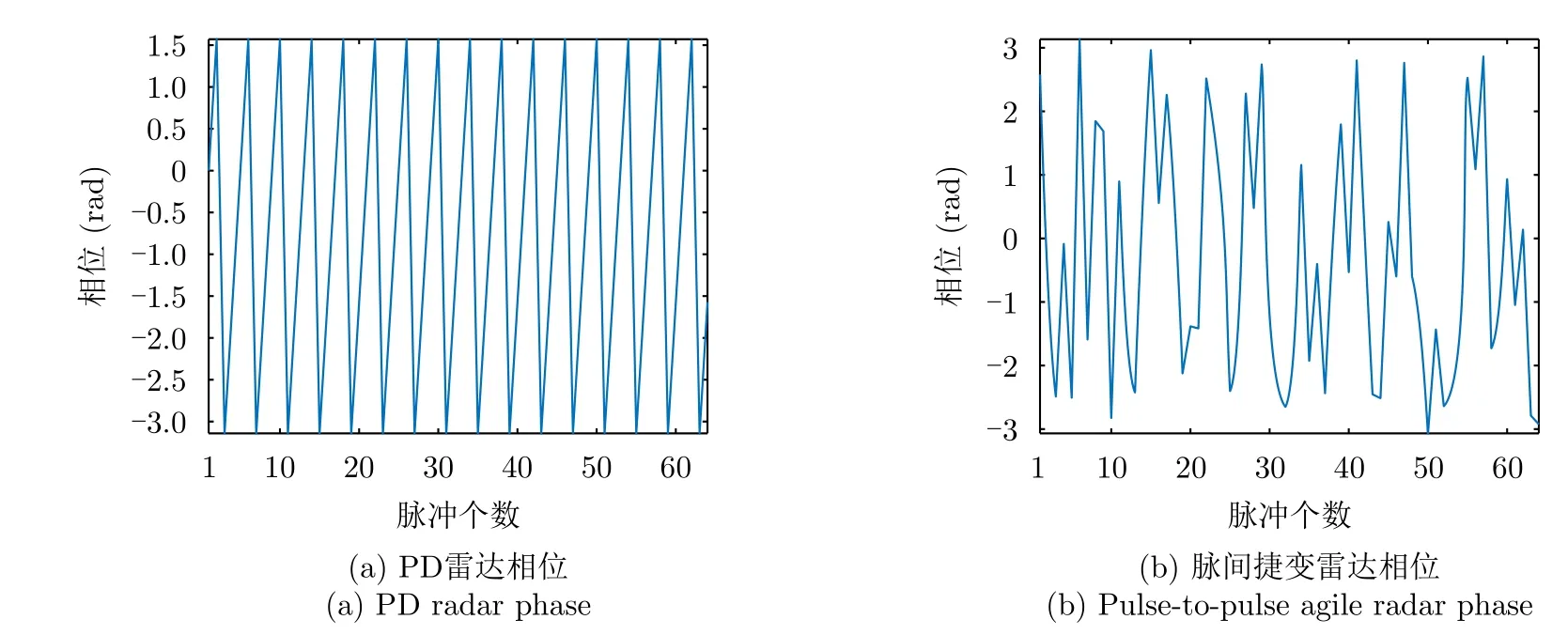
图13 PD雷达与脉间捷变雷达相位Fig.13 Radar and pulse-to-pulse agile radar phase
在随机PRI抖动雷达的信号处理问题方面,稀疏恢复主要被应用于多普勒参数提取与解模糊等应用,文献[103]提出了基于稀疏恢复的重频抖动雷达解模糊算法,并基于加权稀疏重构的方法实现了对杂波的抑制。文献[104]针对假目标场景下变重频雷达稀疏性被破坏的问题,提出了目标与干扰联合稀疏表征的处理方法。
在频率捷变的相参处理方面,基于稀疏恢复的算法在目标距离-速度二维信息重建、边界性能分析等方面取得了丰硕的研究成果。文献[45]基于目标稀疏性,利用压缩感知算法对稀疏步进频信号实现目标参数估计。文献[72]针对距离-速度联合匹配中的网格失配问题,提出了总体最小二乘的自适应匹配追踪算法。清华大学刘一民团队[57,105]对基于稀疏恢复的捷变相参能力边界进行分析与讨论,给出了场景中目标以及杂波个数K的边界,文中指出当(N为脉冲个数,M为载频个数)时,观测场景可大概率被精确重构,进一步地,通过相变图对其性能边界进行表征。在脉间频率捷变的基础之上,对于脉间的载频-重频联合捷变波形的相参处理方面,文献[106]结合载频与重频跳变序列,在脉冲压缩之后构建了与目标高分辨距离-速度信息相匹配的二维字典矩阵,利用OMP实现对目标距离-速度的二维重构。本文结合构建的压缩感知模型,采用OMP算法对脉间捷变雷达进行相参处理[106],并与快速傅里叶变换(Fast Fourier Transform,FFT)算法进行对比,结果如图14(a)所示,由于脉间相位的非线性变化,传统相参处理算法失效,无法完成目标的多普勒测量;如图14(b)与图15(a)所示,OMP算法可对脉间捷变雷达实现有效相参处理,但是采用此种方法进行相参处理时,会存在网格失配的问题,如图15(b)所示,当目标的距离与速度并不在所设的距离-速度网格上时,存在失配问题。

图14 FFT算法与OMP算法Fig.14 FFT algorithm and OMP algorithm

图15 目标所在距离单元的重构结果Fig.15 Reconstruction results for the distance cell where the target is located
在SFA-OFDM波形的相参处理方面,文献[71]针对SFA-OFDM波形的目标参数估计问题,提出了通过对多子载波的压缩感知处理等效合成宽带OFDM,利用目标在距离-速度联合特征域的稀疏性,基于压缩感知对距离-速度高分辨进行估计。文献[78]通过对子载波频移、时移等的操作,将SFA-OFDM波形的相参处理问题转换为捷变雷达的相参处理问题,结合目标场景稀疏性,实现对目标的距离-速度的高分辨估计。
4.4 雷达成像
雷达成像是指对发射的电磁信号的回波进行信号处理,从而得到感兴趣的目标的电磁散射特性信息[107-109]。如3.2节所述,雷达成像回波存在的数据缺失现象会导致孔径稀疏问题,本节对压缩感知成像模型以及稀疏信号处理在SAR与ISAR中的应用展开讨论。
不失一般性地,合成孔径雷达成像观测可表示为[110]
其中,σ(x,y) 表示位于 (x,y)的目标的后向散射,具有随机相位。c表示电磁波速度,f表示载波频率,τ和t分别表示对应距离和方位向的快慢时间。u(τ)表示发射信号的包络。将散射场分解为二维离散网格,并以矢量形式叠加,得到离散化后的观测模型为[110]
其中,s表示采样后的回波数据,x表示待求解的成像结果,表示n噪声,F表示SAR成像过程对应的观测方程,Ψ表示稀疏采样。
压缩感知稀疏成像利用稀疏先验实现对x的重建。对ISAR而言,目标相对背景具有天然的稀疏性,对SAR而言,即使x本身不具备稀疏性,也可利用线性变换x=Φa挖掘其在变换域的稀疏性,因此压缩感知成像模型可统一表示为
其中,‖a‖p表示向量的ℓp范数,ε表示估计的噪声误差。
(1) 压缩感知SAR成像
传统的雷达成像方法在数据大量缺失条件下,存在高旁瓣以及高栅瓣的问题。将压缩感知应用到高分辨雷达成像中,基于雷达成像场景的先验稀疏性,可以从少量的测量数据中重构目标图像,有效缓解数据采集、存储等的压力[111],解决不完整采样条件下的稀疏孔径雷达成像问题。2007年,Baraniuk等人[18]提出了一种低采样率的SAR系统,并通过实验验证了欠采样条件下获取目标高分辨图像的能力。在此之后,稀疏信号处理技术被逐步应用于单基SAR和多基SAR的信号处理中。
在单基地SAR信号处理方面,压缩感知成像技术的研究集中在稀疏孔径条件下高质量成像技术以及性能边界分析等方面。文献[48]提出一种基于CS理论的SAR成像方法,该方法同时在距离维和方位维进行CS反演,在大量原始数据被丢弃的条件下,具备良好的二维成像效果。后续相关学者对成像稀疏表示以及压缩感知理论在不同的成像场景中的应用等方面展开了研究。文献[112]基于小波稀疏表示的SAR成像方法,对随机稀疏采样的数据进行处理,实验结果表明在方位向数据严重降采样的条件下,采用所提算法可以无模糊重构SAR图像。针对聚束SAR成像问题,文献[113]构建了基于CS的成像模型,采用交替迭代思想求解优化问题,实现了目标图像特征增强,同时对有限数据量的目标成像具备鲁棒性。文献[114]通过联合稀疏正则化以及卷积神经网络(Convolutional Neural Network,CNN),设计了一种即插即用框架,实现了聚束式SAR成像。文献[115]将成像自聚焦问题视为一个联合优化问题,在变分最大化期望准则下提出一种联合相位误差抑制的稀疏成像算法,该算法充分利用相位噪声的先验特性以及目标的结构稀疏散射特性,实现了精度较高的相位噪声估计和聚焦良好的成像结果。如图16所示,SAR数据稀疏孔径情况下,由于稀疏孔径导致了多普勒模糊,传统SAR成像结果存在散焦和模糊问题,利用压缩感知[116]能够从稀疏孔径数据重建无模糊SAR图像,但是采用压缩感知技术重构SAR图像时,需要满足稀疏性要求,且使用压缩感知技术时需要考虑运算量的问题。

图16 传统SAR成像算法与压缩感知稀疏成像结果Fig.16 Comparison of SAR imaging results based on traditional algorithm and CS algorithm
多基地雷达系统相较于单基地雷达系统具有更强的灵活性,可从多角度观测获得更多目标信息,但是由于雷达系统接收信息的增加,也意味着雷达系统有更大的数据存储压力。压缩感知理论的应用可以有效解决多基地雷达数据量大以及高分辨能力与雷达系统成本之间的矛盾[117]。文献[118]研究了CS理论在多站SAR场景下运动目标成像问题,并通过仿真说明了压缩感知方法比传统通过匹配滤波方法在自聚焦方面具有更好的性能。文献[119]针对双基地SAR二维高分辨成像问题,将CS理论与双基地SAR模型相结合,测量值采用二维随机降采样回波数据,与传统的双基SAR成像算法相比,基于CS的重建算法具有更高的分辨率,且数据量更少。
(2) 压缩感知ISAR成像
与在SAR中的影响相似,稀疏信号处理技术也用于解决稀疏孔径条件下的ISAR成像处理。通过对实测数据进行随机稀疏采样后,采用基于ℓ1范数的压缩感知(L1-norm CS,L1-CS)算法[120,121]得到不同信噪比下的ISAR成像结果如图17所示,可以看出L1-CS算法可以在稀疏孔径条件实现ISAR成像,但是其成像性能会受到信噪比的影响。利用均方根误差(Root Mean Square Error,RMSE)以及相关系数(Correlation Coefficient,CORR)作为ISAR成像性能评估指标,给出不同稀疏孔径数据条件下的成像性能评估结果,结果如图18以及表2所示,随着稀疏采样率的提升,L1-CS算法的均方根误差逐渐减小,相关系数逐渐提升[121]。本小节结合平稳目标的ISAR成像与机动目标ISAR成像两种场景,对稀疏信号处理在ISAR成像中的应用展开讨论。

表2 成像性能分析Tab.2 ISAR imaging performance analysis
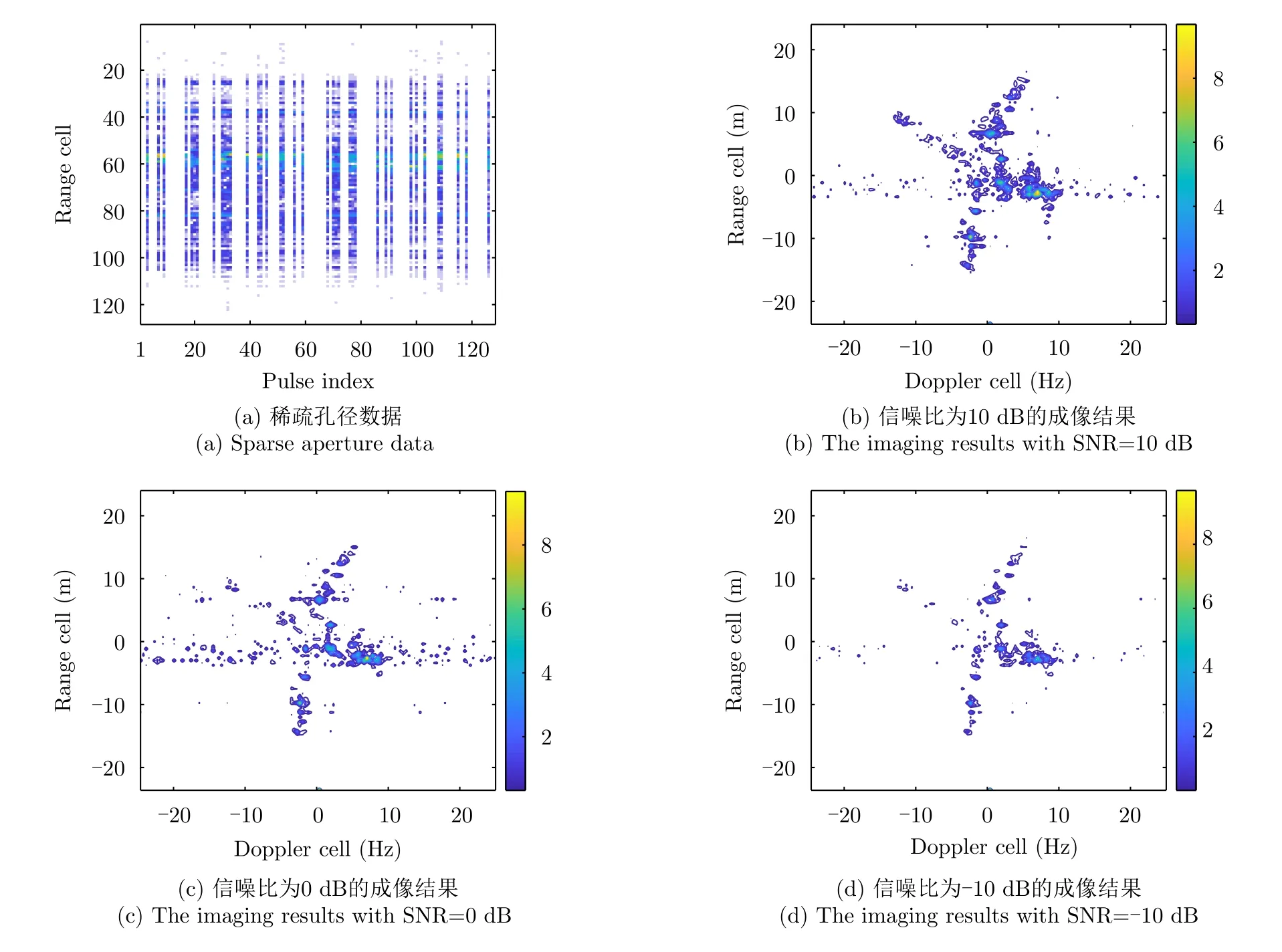
图17 稀疏孔径下的稀疏ISAR成像[120]Fig.17 Sparse ISAR imaging using sparse aperture[120]

图18 ISAR成像性能分析[121]Fig.18 ISAR imaging performance analysis[121]
在平稳目标的ISAR稀疏成像方面,西安电子科技大学邢孟道团队[122]利用CS实现了对目标的超分辨ISAR成像,进一步通过相干投影和加权提高了算法的抗噪以及抗杂波性能,完成对散射中心的精确估计。对于低信噪比场景,文献[123]提出了基于广义柯西分布族中Meridian先验的CS超分辨成像模型。随着脉冲数量和信噪比的降低,该模型在分辨率和幅度误差方面相较于基于拉普拉斯先验的CS模型表现出更好的性能。在杂波场景中,为解决信号与杂波背景难以区分问题,文献[124]结合局部稀疏约束和非局部总变分提出了新的ISAR成像方法,该方法去除虚假的强散射中心或杂波的同时保持了目标区域的形状和几何结构,减少虚假散射点和杂波对ISAR成像的影响。针对欠采样ISAR成像问题,文献[125]提出了一种基于ADMM展开网络成像算法,基于多个可学习的稀疏变换以及可学习的逐点分段线性函数,实现了欠采样条件下的高性能ISAR成像。此外,大量学者开展了相位误差校正方面的研究工作[126],提高了 CS 成像算法的鲁棒性。
机动ISAR目标的回波信号在一定匹配傅里叶域具有稀疏性,文献[127]提出了适用于随机稀疏孔径和短孔径情况的基于压缩感知的ISAR成像方法,该方法考虑了稀疏字典对相对旋转参数的依赖性,并利用分数傅里叶域最优搜索的参数估计方法实现参数估计,实现了良好的成像效果。文献[128]利用目标场景的稀疏空间特性来描述其在时频域中的回波信号的稀疏性,构建基于瞬时傅里叶变换的字典并将距离-瞬时多普勒(Range-Instantaneous Doppler,RID)成像转化为稀疏重建问题,然后采用迭代加权策略实现信号增强和噪声抑制。
4.5 雷达目标检测
在现代雷达通常采用恒虚警率(Constant False Alarm Rate,CFAR)进行目标检测,在杂波或者存在干扰的场景中CFAR的检测门限会随着参考单元变化而自适应改变,从而完成恒虚警目标检测。CFAR作为一种经典的目标检测方法,其理论研究与工程应用方面均得到了不断的发展与完善[129],但为了减小雷达处理数据量,将压缩感知运用在CFAR中成为一种研究趋势,在拓展目标检测等应用中取得了广泛应用。假设雷达系统发射信号为步进频,第q个脉冲串经过鉴相器后的输出表示为[130]
其中,R和v分别表示目标的距离和速度,c为光速,fq为第q个回波信号的载频,T为雷达发射信号的脉冲重复周期。根据压缩感知理论可将鉴相器的输出改写成矩阵的形式:
随机抽取Ψ中的n行作为观测矩阵,该过程可描述为
n′是复高斯噪声。将式(23)转化为以下无约束问题:
其中,λ表示松弛因子。
目前基于压缩感知框架实现目标检测方面的研究成果颇多,文献[131]通过设计一种建立在压缩域上的分布式单元平均恒虚警(Cell Averaging-CFAR,CA-CFAR)检测器和适用于压缩检测的门限选定方法,可在低SNR下直接实现目标检测,无需重构,节省了运算量。另外,基于压缩感知将CFAR与其他算法联合也有优异的性能,文献[132]针对基于压缩感知的CA-CFAR检测器在相近目标检测性能下降的问题,提出了一种基于压缩感知的可变标识恒虚警检测算法(Compressive Sensing Variable Identification-CFAR,CSVI-CFAR);清华大学刘一民团队[133]针对行正交设计模型下压缩感知传感器的目标检测问题,提出了一种去偏LASSO检测器的设计,相较于传统的压缩感知检测器和其他去偏的LASSO检测器而言,该检测器可以根据给定的误报率进行分析提供阈值且具有更优的检测性能。文献[134]基于压缩感知理论,分析高分辨率范围剖面(High Resolution Range Profile,HRRP)可以通过ℓ1范数最小化从低维压缩感知测量中获取,利用统计特性和显性散射体,提出一种新的恒虚警检测器来检测复高斯噪声中的距离扩展点目标。
5 结语
将雷达场景中的稀疏性作为目标参数估计与雷达成像的约束条件,可以有效提升传统雷达信号处理的性能,或者解决新雷达体制下传统信号处理方法不适用的问题,因此稀疏信号处理技术在雷达数字信号处理的各个阶段都得到了广泛的应用。随着雷达技术的不断发展,新的雷达体制、雷达系统设计、雷达观测方法也层出不穷,美国国防高级研究计划局也推出了其超线性信号处理的雷达发展项目,拟在通过雷达信号处理的方法提升雷达在硬件受限条件下的探测能力,信号稀疏表示法也被视作其中的重点处理技术。总而言之,得益于雷达探测场景中的稀疏先验条件,稀疏信号处理将雷达信号处理技术的发展中继续发挥持续而深刻的作用。
利益冲突所有作者均声明不存在利益冲突
Conflict of InterestsThe authors declare that there is no conflict of interests
