星载SAR 图像方位角计算及其对风速反演影响评估*
2024-01-21李慧敏胡登辉林文明何宜军
李慧敏 胡登辉 林文明 王 臣 何宜军
1(南京信息工程大学海洋科学学院 南京 210044)
2(自然资源部空间海洋遥感与应用重点实验室 北京 100081)
3(中国科学院微小卫星创新研究院 上海 201203)
0 引言
自1978 年全球首颗卫星SEASAT-A 发射成功以来[1],星载合成孔径雷达(SAR)经过40 多年的快速发展,已成为地球表面常规监测的重要手段之一。特别是SAR 对于海面的观测及关键物理参数提取,为物理海洋、生态环境及海气相互作用等科学研究提供了重要数据[2-6]。国际SAR 卫星计划的引领与持续投入主要以中国和欧洲为主,例如欧洲空间局的哨兵一号卫星(Sentinel-1)和中国的高分三号卫星(GF-3)、1 m C-SAR 等。其他卫星计划也日渐增多,涵盖不同波段、不同极化、不同轨道和不同数据获取模式,为实现多颗SAR 卫星的星座组网观测奠定了坚实基础。星载SAR 卫星得到广泛重视的原因在于其全天候、全天时、高分辨率的数据优势,这对于地球表面持续监测、定位关键目标信息、响应环境高频突发事件、聚焦亚中小尺度圈层科学问题等有切实效益。
SAR 卫星数据的应用涵盖海洋学多个研究领域,雷达后向散射信号主要由海面布拉格波贡献,其他尺度海洋现象通过改变或调制海面粗糙度,可以在SAR 图像上留下不同散射信号特征[7]。在过去几十年里,对于SAR 后向散射信号的处理算法逐渐成熟,发展了针对不同SAR 卫星的绝对定标、辐射定标、数据分级、参数反演等业务化流程,为SAR 数据分发共享与科学应用提供了诸多便利[8]。然而,SAR 数据使用过程中最常用到、又容易被忽略的是方位角信息,即SAR 图像方位向在对应地球坐标投影下相对于地理北极的角度大小[2,7]。该角度准确与否直接影响地球方向性物理参数的反演精度,也间接影响反演过程中需要使用方位角信息的物理参数精度。随着SAR 数据业务化服务的不断提高,各级数据中经常提供多个角度参数,对其仔细筛选和应用尤为重要,往往决定着后续研究中是否会引入系统性误差。
在与SAR 图像方位角有关的众多地球物理反演参数中,海面风场是最常见的一个,其算法原理与散射计海面风场反演相似,都是通过建立海面10 m 高度处近中性风场矢量与后向散射系数及入射角、极化、波段等雷达参数的经验关系,构建地球物理模式函数(Geophysical Model Function,GMF)[9]。其中针对C 波段散射计的CMOD 是应用最为广泛的GMF[10,11],该系列函数一直在不断的改进与提高。在CMOD4 函数建立不久,Alpers 和Brümmer 就将其应用到ERS-1 的SAR 图像海面风场反演研究中[12]。基于SAR 反演数据,Young 与Mourad 团队对海面风场精细结构进行深入探究,为揭示海洋大气边界层千米尺度动力过程开拓了思路[13,14]。随后,Mouche等[15]针对星载C 波段SAR 后向散射数据开展了系统研究,在综合考虑海面电磁散射特性及不同风力作用下的波浪情况,进一步改进发展了C-SARMOD 函数,可以较好地应用于哨兵一号SAR 数据的风场反演。
1 星载SAR 成像与坐标系统
1.1 星载SAR 成像几何
需要特别指出的是,SAR 作为单天线观测设备,无法像散射计一样独立提取风向,SAR 风速反演依赖外部风向输入,同时因为GMF 表征的是雷达后向散射系数与相对风向的关系,即顺风方向与SAR 雷达视向的夹角,计算该角度大小同时需要确定图像方位角信息。为形象简明地展示星载SAR 成像几何关系,很多现有图文资料[2,7]以图1(a)所示为主,这类概念图容易产生图像方位角ϕIMG等于卫星飞行方向ϕSAT的误导信息。相比之下,图1(b)给出了考虑地球表面为曲面的SAR 卫星成像关系,可以看出ϕIMG与ϕSAT存在差异,两者之差与星载SAR 信号处理、空间投影和坐标系转换有密切关系。本文以欧洲空间局哨兵一号波模式(Wave mode, WV)SAR 数据为例,首先概述星载SAR 成像原理与坐标转换数学关系,明确ϕIMG与ϕSAT无法等同的原因;然后给出基于地面控制点(Ground Control Point,GCP)的ϕIMG计算方法,并统计分析其与ϕSAT的关系;最后对比ϕIMG和ϕSAT用于SAR 风速反演的精度差异。为了最大程度量化SAR 图像方位角的影响,实验数据选取不受其他海洋大气现象影响的SAR 数据[6],风场参考资料选用欧洲中期天气预报中心的ERA5 再分析数据,时间分辨率为逐小时,空间分辨率为25 km。本文内容将对SAR 图像方位角的正确计算及其在海面风场反演中的影响起示范作用。
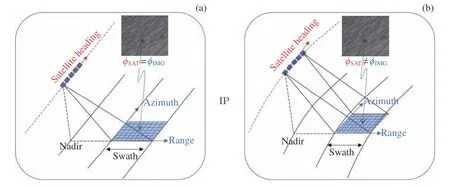
图1 不考虑(a)和考虑(b)地球曲面的星载SAR 成像几何概念。ϕSAT 和ϕIMG 分别为卫星飞行方向和SAR 图像方位向与地理北极的夹角Fig. 1 Illustration of SAR imaging geometries without (a) and with (b) consideration of the curved Earth’s surface.The satellite heading ϕSAT is the angle of its flighting direction relative to the North. The image heading ϕIMG is the angle of geolocated azimuth direction of each pixel relative to the North
SAR 传感器大多以线性调频信号的方式发射电磁波,即发射波形幅度在脉冲时间τ内保持恒定,而瞬时频率fi=krt随着时间t以线性方式进行变化,其中kr为线性调频频率,kr与τ决定了波形产生带宽Br=krτ。每一个τ之后是雷达接收回波窗口时间,并将接收到的回波强度存储下来。所以SAR 在卫星飞行过程中,持续不断的向与飞行方向垂直的径向发射和接收电磁波,其数字信号处理涉及很多方面,与空间几何相关的包括:确定从卫星到地球表面任何点目标的斜距距离;确定每一时刻雷达信号在卫星参考坐标系中的位置;根据精确卫星轨道参数,确定卫星坐标系与地球地理坐标系的转换。根据SAR 信号数据的不同视角,可以归纳为图像信号坐标系、空间卫星坐标系和地球地理坐标系,三者之间的关系及转换如图2 所示。
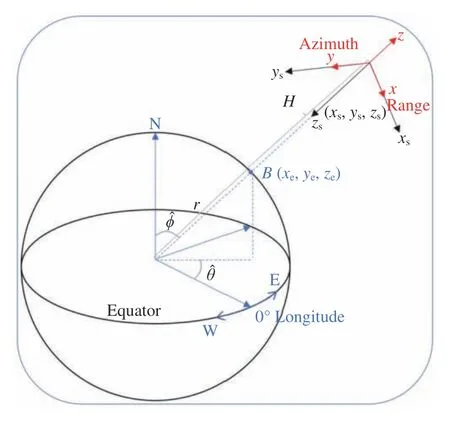
图2 星载SAR 图像信号坐标系(红色)、空间卫星坐标系(黑色)与地球地理坐标系(蓝色)的关系Fig. 2 Spaceborne SAR coordinate systems from image signal (in red) to satellite-centered (in black)and the Earth-centered (in blue)
1.2 图像信号坐标系
图像信号坐标系是指SAR 数字信号对于轨道时间轴的记录方式,在右手笛卡儿坐标系中,定义x轴为雷达径向方向,y轴为雷达沿轨方向,z轴为雷达信号强度,如图2 红色箭头部分所示。x轴记录每个雷达脉冲的回波时间,根据脉冲返回时间将其划分为斜距单元;y轴记录所有雷达脉冲时间,根据脉冲重复频率划分为方位向单元;z轴记录点目标(τ,t)的反射强度S。这实际是对SAR 信号传播轨迹的解码和转换,即对于某一个脉冲时间τm和沿轨时间tk,利用多普勒频率进行方位向压缩。在此过程中,可以确定径向的单元分辨率为δr=c/(2Br),其中c ≈3×108m·s-1为光速;而方位向分辨率δa=da/2由合成孔径算法所得[2],其中da为雷达天线长度。
1.3 空间卫星坐标系
空间卫星坐标系(xs,ys,zs)是指原点在卫星质心的右手笛卡儿坐标系,用于较好实现图像信号坐标系和地球地理坐标系之间的转换,如图2 黑色箭头部分所示,其中zs是卫星质心指向地球质心的方向,xsys面与zs垂直且ys与卫星飞行方向(即沿轨方向)一致。对于任何一个图像信号坐标(τm,tk),其与空间卫星坐标系(xs,ys,zs)关系为
其中,H为卫星轨道半径,和分别为纬度和经度对时间的一阶导数。对于圆形轨道,H对时间的导数为0,所以式(1) 可简化为
1.4 地球地理坐标系
如图2 中蓝色部分所示,地球地理坐标系(xe,ye,ze)是指原点在地球质心的经纬度坐标系,对于某一经度为θe和纬度为ϕe的点, 其坐标为(recosθecosϕe,resinθecosϕe,resinϕe),其中re为地球半径。同样对于经纬度为的卫星位置B可表示为(Hcoscos,Hsincos,Hsinϕ︿),其中H为卫星轨道半径。(xe,ye,ze) 与(xs,ys,zs)的坐标转换可以通过移动卫星位置B以及旋转矩阵M来实现,即
其中,
通过式(2)和式(3),可以建立SAR 数字信号坐标(τm,tk)与地球地理坐标系(xe,ye,ze)的数学关系,详细推导和原理参见文献[16-18]。一个星载SAR 传感器的发射到业务化运行,首先需要进行周密的在轨测试,其中一个基本步骤就是对SAR 图像进行地理编码/解码和精确定位,目前最主流的方式是利用GCPs 确定卫星姿态及坐标系转换中所使用的参数,所以在每一景SAR 图像数据中,都会对应提供一定数量的GCPs。
2 合成孔径雷达图像方位角计算方法
从SAR 获取的原始信号推导图像方位角需要精确的卫星轨道、卫星姿态和SAR 成像算法信息,过程复杂且不利于实际应用推广[19,20]。相比之下,SAR数据中提供的GCPs 经过严格推算和验证,SAR 图像中的像素点精确对应地球地理坐标系下的经纬度,可以用于SAR 图像方位角的快速高效计算。对于哨兵一号 WV 数据,每一景SAR 图像宽度和长度分别为约为20 km,含有77 个GCPs,如图3 所示。该两景图像案例均位于陆地边缘,海岸带信息清晰可见,通过对比图像陆地边缘与背景地图边缘,佐证了SAR 图像像素与地理经纬度是一一对应的,大量相关研究工作也已经量化了这一准确性[21,22]。
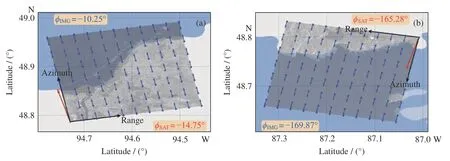
图3 哨兵一号波模式SAR 图像升轨(a)与降轨(b)案例。蓝色点为GCPs 位置,蓝色箭头为利用GCPs 计算的图像方位角ϕIMG,红色箭头为卫星飞行方向ϕSATFig. 3 Two Sentinel-1WV cases of ascending (a) and descending (b) showing the GCPs in blue points,ϕIMGcalculated using GCPs in blue arrows and ϕSAT in red arrows
从图3 可看出,GCPs(蓝色圆点)相对于SAR 图像是均匀分布的,图像方位角可看作是同一方位向上两个GCPs 的方向角,如图3 中的蓝色箭头指示相邻GCPs 的方向角。这一计算方式可追溯到大航海时代,用于查找地球上两点之间的航向角,目前仍广泛应用于航空、航海和陆地导航等领域[23]。当假设地球为规则圆球形时,经纬度为(θ1,ϕ1) 和(θ2,ϕ2)的A,B两点方向角ϕB计算公式为
然而地球是以赤道半径a=6378.137 km、极半径b=6356.752314245 km和扁率f=(a-b)/a的椭球体,需要使用更为精确的计算方法,例如Vincenty[23]提出的实现算法如下:
步骤1计算相关参数。
步骤2迭代计算以下参数,直到λ(初值为L)变化非常小。
步骤3计算方位角ϕB。
利用该方法,计算图3 所示两个案例的图像方位角,发现在整景SAR 图像刈幅宽度内,基于不同方位向上GCPs 数据点对得到的方位角变化非常小(均方根小于0.2°),这是因为地球表面在较小范围内可以近似为平面。图3 中的ϕIMG为各自图像方位向第一个GCPs 点对的计算结果,与数据中提供的卫星飞行方向ϕSAT相比(红色箭头所指),存在明显的差异。具体而言,ϕSAT明显偏离了SAR 图像方位向,而基于GCPs 计算的ϕIMG与理论SAR 图像方位角吻合。
3 哨兵一号波模式图像方位角与卫星飞行方向对比
为深入探究哨兵一号波模式 SAR 数据的图像方位角与卫星轨道方向角之间的偏差,本研究基于2016 年获取的约70 万景开阔大洋SAR 数据,统一计算了ϕIMG与ϕSAT的数值,并将两者偏差的全球空间分布以2.5°×2.5°经纬度网格显示,如图4 所示。图4(a)~(d)分别对应23°入射角(WV1)升轨(ASC)、23°入射角降轨(DSC)、36°入射角(WV2)升轨、36°入射角降轨情况,颜色代表平均差值大小。由此可以发现,卫星升轨轨道的ϕIMG-ϕSAT值在南半球为负值,在北半球为正值,且数值大小随着纬度的升高而逐渐变大。对于两个入射角,ϕIMG与ϕSAT两者角度差在赤道都为0°,而在高纬度60°S 和60°N,WV1 分别约为-3°和3°,WV2 分别约为-6°和6°。降轨ϕIMG-ϕSAT随纬度变化趋势与升轨恰好相反,但角度差值的数值大小在相同纬度保持一致。结合图1(b)可以推断,在同一纬度下ϕIMG-ϕSAT随传感器入射角增大而变大,当入射角为0 时(即星下点),图像将被压缩成一条线,方位角与卫星飞行方向一致。同样结合图3 可知,哨兵一号为右视SAR 雷达传感器,升轨时卫星在北半球由赤道向极地飞行,雷达距离向扫描的经度覆盖区间逐渐较小,卫星高度处(H >re)相较于地球表面(re)的方位向更加偏离地理北极,导致ϕIMG>ϕSAT。在南半球时,降轨可以看作是北半球的升轨,因而与升轨的ϕIMG与ϕSAT变化规律相反。
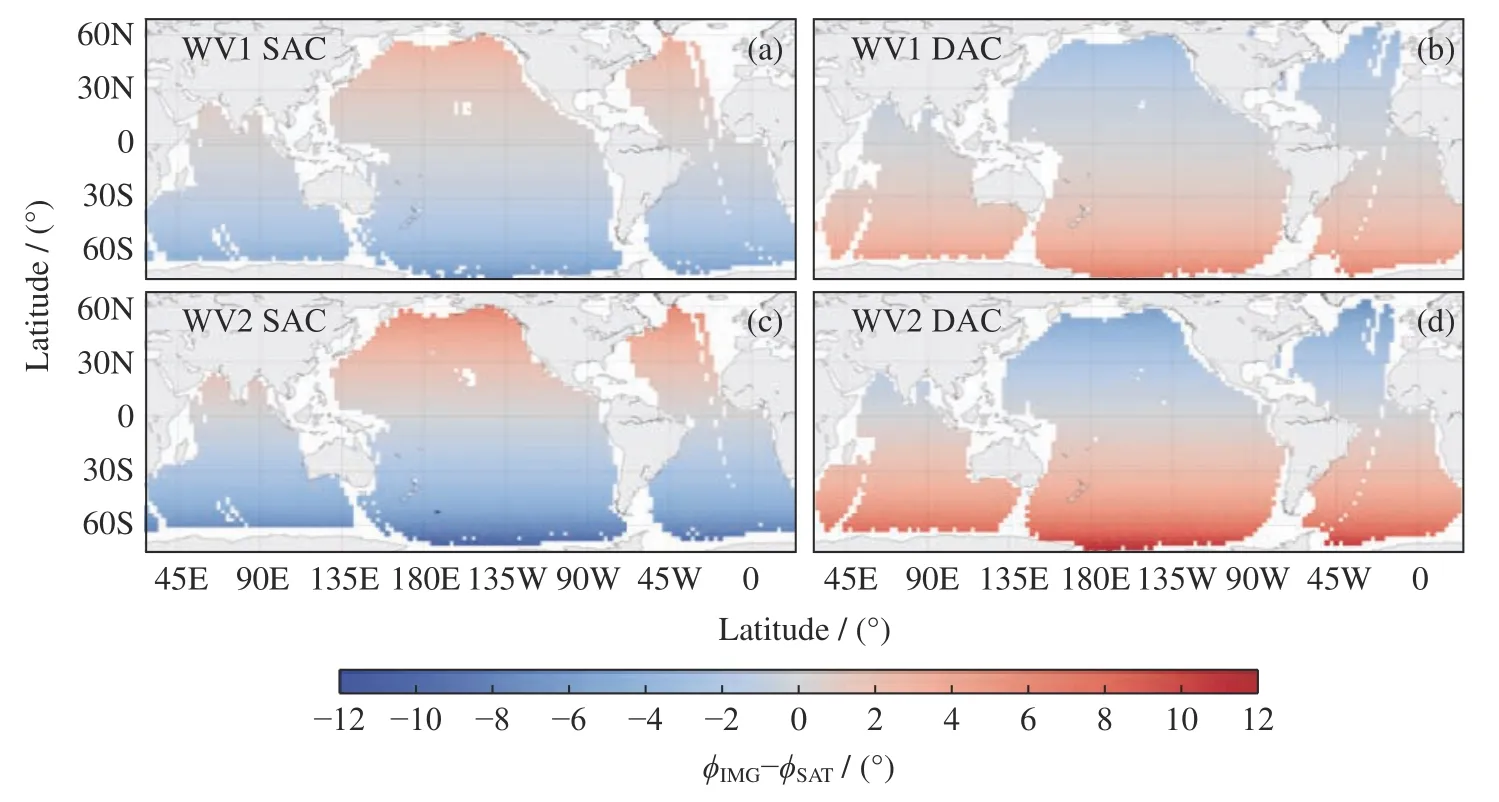
图4 2016 年全球哨兵一号波模式SAR 图像方位角ϕIMG与卫星飞行方向ϕSAT差值分布。 (a)和(b)分别为WV1(23°入射角)升轨与降轨。(c)和(d)分别为WV2 (36°入射角)升轨与降轨Fig. 4 Global maps of the difference between image heading ϕIMG and satellite heading ϕSAT for S-1 A WV1 ASC(a), WV1 DSC (b), WV2 ASC (c) and WV2 DSC (d) SAR data acquired in 2016
图5 分别给出了WV1 升轨与降轨以及WV2 升轨与降轨ϕIMG-ϕSAT随纬度的散点分布,从图5 中可以看出,除极个别异常点外(地面处理系统升级导致)ϕIMG-ϕSAT与纬度的非线性关系在特定入射角和升轨/降轨时非常固定。研究表明,五次多项式对该关系的拟合误差小于0.001°,有
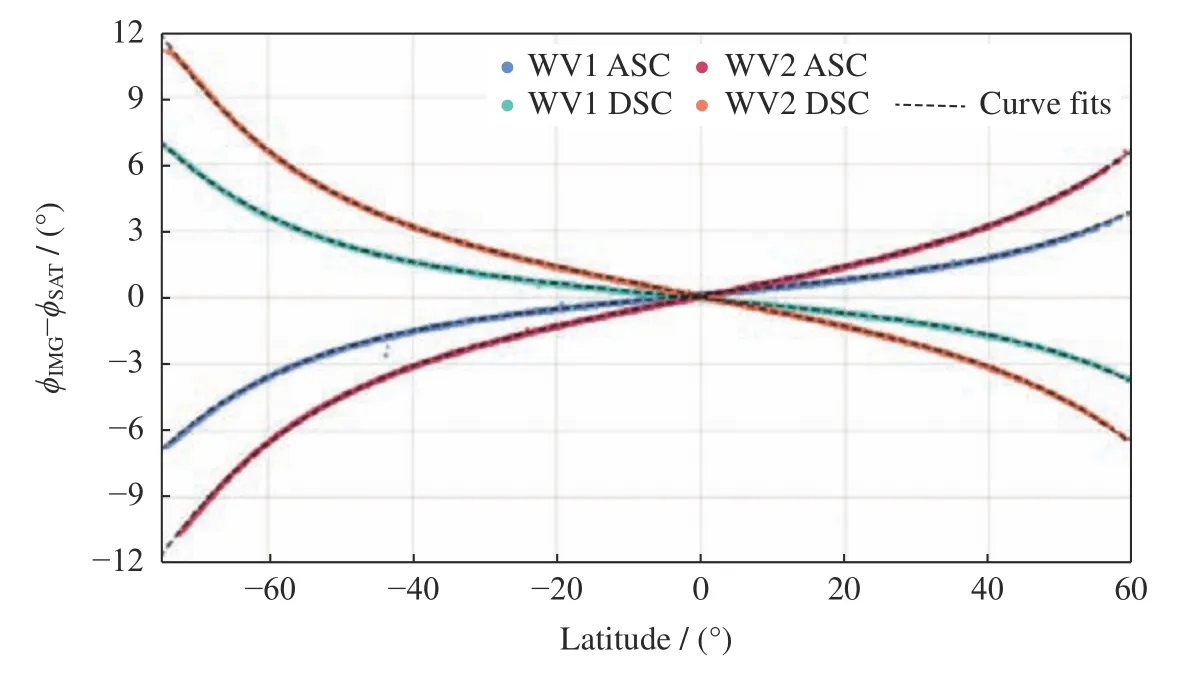
图5 2016 年全球哨兵一号波模式SAR 图像方位角ϕIMG与卫星飞行方向ϕSAT的差值散点图。黑色虚线为利用五次多项式对WV1 升轨与降轨和WV2 升轨与降轨数据的拟合,拟合参数见表1Fig. 5 Scatters of the difference between image heading ϕIMGand satellite heading ϕSAT along latitude for S-1 A WV SAR data acquired in 2016. Curve fits in dashed lines are performed using the fifth order polynomial function with coefficients listed in Table 1
拟合系数如表1 所列。利用式(6)和表1 系数,根据一级和二级数据中给定的卫星方位角ϕSAT可直接计算每一景哨兵一号波模式图像的图像方位角ϕIMG,避免反复读取GCPs 导致的计算量,这对于实际地球科学研究应用十分有效,同时对于20 km 幅宽的波模式SAR 图像,方位角在有限空间范围内的变化可忽略不计。值得注意的是,该图像方位角矫正偏差拟合公式只适用于哨兵一号 WV 数据,对于哨兵一号其他模式SAR 数据,需要重新利用相应的GCPs进行计算,且宽刈幅的SAR 图像因方位角变化较大,不能使用单一数值替代。

表1 图5 中五次多项式对WV1 升轨与降轨和WV2 升轨与降轨数据的拟合系数Table 1 Coefficients of the fifth order polynomial fit of the curves shown in Fig. 5
4 图像方位角对海面风场反演精度的影响
SAR 图像方位角和卫星轨道角之间存在的系统偏差,会直接影响与方向相关的地球物理参数提取,例如海浪方向、海面风向、海洋内波传播方向等。从SAR 图像中得到的方向信息一般以SAR 图像坐标系为参考,也就是以SAR 图像方位向为0°角,当需要转换为以北极为0°角的地球地理坐标系时,需要输入SAR 图像方位角大小。此时若默认ϕIMG=ϕSAT,就会引入上述如图4 和图5 所示的系统误差,该误差随纬度增加而变大,最大可达10°以上;且对于升轨和降轨轨道,该误差数值互为相反数,这对于分析某一地球物理现象的日变化有不可忽视的影响。同时由图4和图5 可知,当不区分升轨和降轨而进行空间平均时,ϕIMG与ϕSAT之间的偏差会相互抵消。由于目前绝大多数与方向相关的研究以统计为主,且物理参量的均方根误差在30°左右,导致卫星轨道角引起的误差尚无法得到报道,图像方位角的准确计算方法也没有明确指出和重视。
特别需要说明的是,SAR 图像方位角引起的偏差会进一步累积影响相关物理参数的反演。以海面风速反演为例,一般已知SAR 后向散射系数及入射角、极化、波段等雷达参数,但相对风向需要外部绝对风向和ϕIMG共同确定,然后再结合经验GMF 函数经过最小二乘法得到风速数值。毫无疑问,当ϕIMG角度值不准确时会使相对风向存在误差,进而导致风速反演的误差。图6 给出了2016 年哨兵一号波模式 SAR数据利用ϕIMG和ϕSAT进行风速反演的偏差,颜色代表2.5° ×2.5°经纬度网格内的偏差均值。为了量化图像方位角对SAR 风速反演的影响,使用同一个外部输入风向,即对于每一景SAR 图像,在时间和空间上将ERA5 再分析数据的10 m 高度风矢量进行插值,以获取最佳匹配数据,同时使用同一个C-SARMOD GMF,这样就保证了对于同一个SAR 数据,风速反演的唯一变量是图像方位角。总体而言,不同入射角和轨道方向反演的两者风速偏差大小有所差异,36°入射角的风速偏差大于23°入射角,这是因为大入射角下的ϕIMG与ϕSAT偏差更大,引起的相对风向偏差也更大;然而不同于图4,风速偏差的正负对于升轨和降轨并不是相反的,这是因为风速反演数值与相对风向紧密相关,而非简单的线性关系。
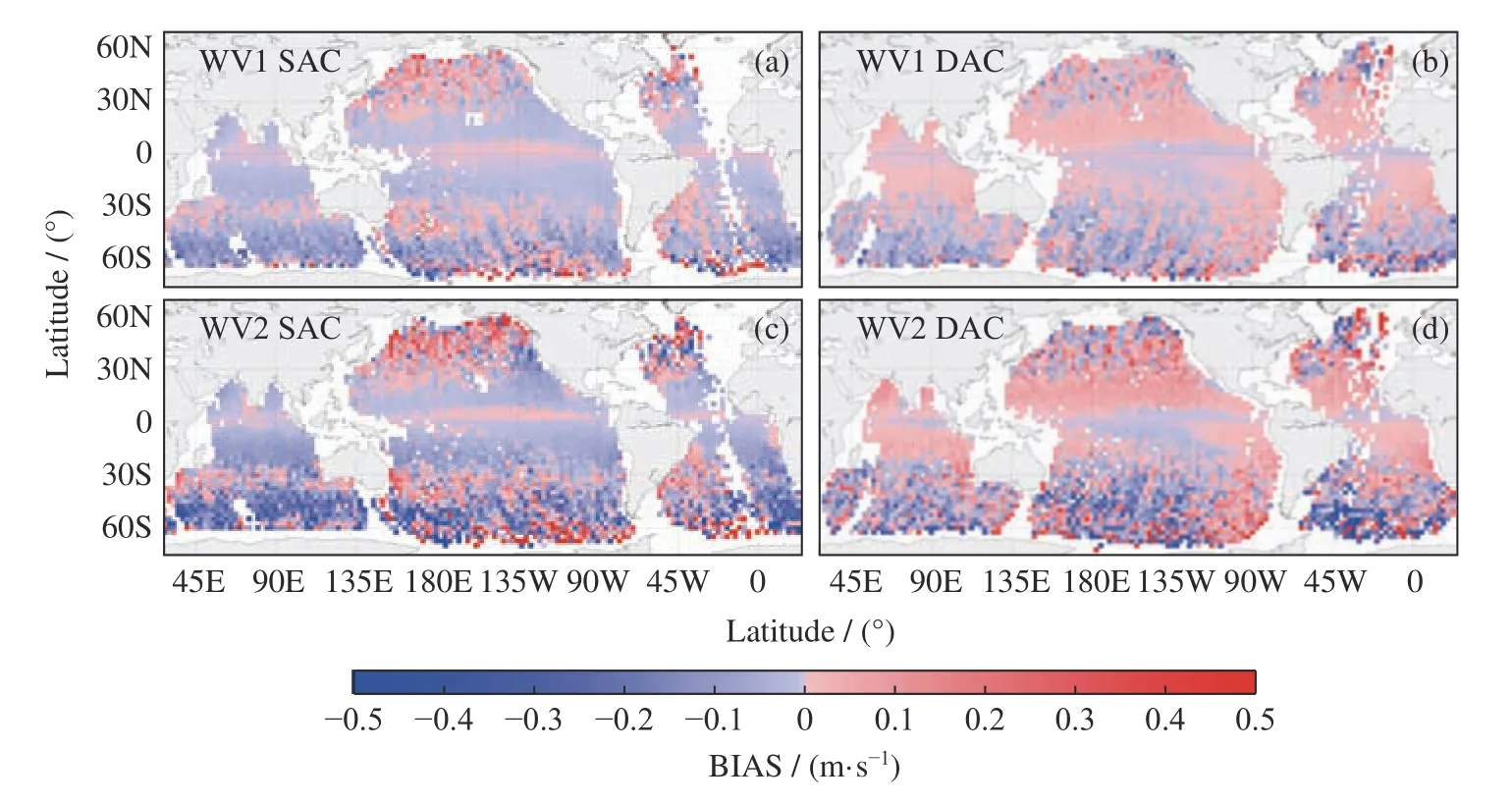
图6 利用ϕSAT 和ϕIMG对2016 年全球哨兵一号 WV SAR 数据进行风速反演的偏差。(a)和(b)分别为WV1(23°入射角)升轨与降轨。(c)和(d)分别为WV2 (36°入射角)升轨与降轨。反演算法统一使用C-SARMOD GMF 和ERA5 再分析数据的10 m 高度处风向。正值和负值分别代表高估和低估Fig. 6 Global mean biases of SAR retrieved sea surface wind speed using between the satellite heading and image heading. (a) and (b) are WV1 ascending and descending, and (c) and (d) are WV2 ascending and descending, respectively. The C-SARMOD GMF is used with wind direction inputs of ERA5 U10.Positives and negatives here mean overestimates and underestimates, respectively
从图6 可以看出,使用ϕIMG=ϕSAT所引起的风速反演误差是不能忽视的。哨兵一号波模式的两个入射角风速误差在全球空间分布对于升轨或降轨是相似的,升轨时除赤道附近、北半球中高纬和30°S 附近外,总体为负值;降轨时除南半球中高纬外,总体为正值。然而对于同一入射角,升轨与降轨的风速偏差并不能抵消,且大入射角下的风速误差更大,可达±0.5 m·s-1。因此,正确使用SAR 图像方位角对于海面风速反演影响显著,尤其是对于探究风速的早晚差异性。另外,哨兵一号波模式作为当下唯一在开阔海洋持续收集数据的SAR 卫星,可以提供超高分辨率的海面风场数据,对于高分辨率的数值模式同化有巨大应用潜力。为保障SAR 海面风场的反演精度,明确SAR 图像方位角的定义、计算、使用及其对风速反演精度的影响,也是十分必要的[24,25]。
基于ϕIMG和ERA5 的外部风向,进一步评估哨兵一号波模式SAR 数据全球开阔海洋风速反演的精度,参考资料为ERA5 10 m 高度处的风速,如图7 所示,其中颜色为归一化到0~1 的数据密度。对于两个入射角和升轨/降轨,SAR 反演风速与ERA5 风速的平均偏差在0.35 m·s-1以内,表现为略微高估,标准差在1.3 m·s-1左右。相比于全球散射计风速1.5 m·s-1的总体统计误差[24],开阔海洋的波模式SAR 反演风速具有很高的精度,这不仅仅因为可以通过机器学习智能分类[6],最大程度上去除了SAR 数据中其他海洋大气现象的影响,也得益于对SAR 数据处理的严格要求。鉴于SAR 高分辨率的优势特点,其在提供高分辨率海面风场的潜力不可忽视,对当前海气界面千米尺度动力过程的研究具有重要意义。

图7 利用ϕIMG的2016 年全球哨兵一号波模式 SAR 数据风速反演精度。(a)和(b)分别为WV1 升轨与降轨。(c)和(d)分别为WV2 升轨与降轨。对比风速为ERA5 再分析数据Fig. 7 Accuracy of wind speed retrieved using ϕIMG from the Sentinel-1 WV SAR data in 2016. (a)~(d) are for WV1 ASC, WV1 DSC, WV2 ASC and WV2 DSC, respectively. The reference wind speed is from ERA5 reanalysis product
5 结语
星载SAR 作为海洋观测的重要手段之一,在过去几十年的发展和应用中展现出巨大的潜力,SAR 获取的高分辨率海面粗糙度图像,可以为海洋与大气千米尺度物理过程提供数据保障,有效服务地球科学国际研究。然而在涉及SAR 图像方位角的物理参数提取和反演中,一直存在疑问和误用的情况。对此,本文基于2016 年哨兵一号全球波模式数据,详细阐述了SAR 图像方位角的推算方法,及其与卫星轨道方位角的区别;在推导SAR 空间坐标转换的过程中,厘清了SAR 成像中的几何变化关系;提出利用GCPs 计算SAR 图像方位角的方法,并利用个例和统计数据进行对比分析,发现ϕIMG与ϕSAT存在系统偏差,且该偏差与入射角和轨道方向有关;在此基础之上,进一步分析了使用ϕIMG与和ϕSAT对海面风速反演的影响,通过量化两者之间的偏差大小,指出ϕSAT会导致最大±0.5m·s-1的风速反演误差。本文研究明确了SAR 图像方位角的计算方法,指出了其在海面风场反演中的重要性,可以便利地迁移应用于其他SAR 卫星数据的业务化算法。同时,本文详细阐述了SAR 图像方位角与卫星轨道角的概念和两者差别,并以实际观测数据进行对比展示,这对于的SAR 的入门使用群体具有明确的示范作用。
SAR 图像方位角不仅对海面风场反演有影响,其对任何方向性的SAR 物理参数提取都至关重要。当前哨兵一号全球波模式数据使用中,尚没有文献报道该如何计算图像方位角,已有的波模式数据(例如海浪和海面风场)都是默认使用卫星轨道方位角进行替代,这一近似导致的偏差是不可忽略的。本文明确了图像方位角的正确计算和使用方法,弥补了业界对于这一参数认识和重视的不足,对后续海洋SAR 图像数据处理和科学应用具有重要的参考意义。
致谢本文使用的哨兵一号波模式数据由欧洲空间局提供,该数据可通过网站https://www.esa.int/获取。欧洲中期天气预报中心再分析风场数据由ECMWF 气象存档与检索系统提供,该数据可通过https://www.ecmwf.int/公开获取。
