台阶法施工时台阶长度对富水隧道稳定性影响研究①
2024-01-20鲁军纪闫小兵赵培东
鲁军纪, 程 鑫, 闫小兵, 赵培东
(1.湖南涟邵建设工程(集团)有限责任公司,湖南 长沙 410001; 2.中南大学 资源与安全工程学院,湖南 长沙 410083)
作为地下重要构筑物,隧道在保护自然环境、提高运输能力以及加大空间利用率方面发挥着重要作用[1-5]。 随着时代不断发展,隧道工程项目增加,施工条件也日渐复杂,尤其当隧道穿过富水土体时,人为破坏原有地下水渗流,会造成地下水以滴流、股流以及大范围突水等形式向外排出,不仅会增加隧道施工难度,还会影响隧道结构稳定。 因此,研究富水条件下隧道稳定性对提高施工效率和保障隧道安全具有重要作用。
目前,诸多学者分别从地质结构、降水强度、支护方式等角度研究了富水隧道稳定性影响因素[5-12],并据此提出了相应的隧道涌水治理措施。 但已有研究较少从开挖方式角度对富水隧道稳定性进行分析。 台阶法作为隧道施工的常用方法,在多种工况条件下应用广泛,台阶步距的选择是影响施工效率和安全的重要环节。 本文以四川小麻柳尾矿库主隧道工程为例,构建三维数字模型模拟施工过程,综合渗流场、位移场、应力场以及塑性区等计算结果分析不同步距条件下台阶法开挖对富水隧道稳定性的影响,以期为类似工程项目施工设计提供参考依据。
1 工程概况
小麻柳尾矿库地处四川省西昌市太和镇安宁河西岸小麻柳冲沟,初期坝坝址距安宁河西岸约1 800 m。尾矿库原始形态西、北、南三面环山,总体地势由西向东倾斜,库区上游谷地区域由东西向及北东向两条支沟组成,初期坝位于两沟东侧交汇处,库区内地表分水岭北面标高1 650~1 850 m、南面标高1 660~1 840 m、沟底标高1 559~1 563 m,地表地形最大高差超过300 m。
尾矿库截排洪主隧道全长2 377 m,其中压坡段、加高段及渐变段长80 m,暗挖隧道洞身段长2 295 m,隧道上游标高1 661.333 m、下游出水口标高1 596.5 m,库区内隧道总长度为628.812 m,洞身段采用圆拱直墙式断面。 根据围岩条件进行分类,选取主隧道段K2 +234.00~+139.00 m 进行研究,该段为Ⅳ级围岩条件,隧道埋深94.903 ~113.380 m,上覆围岩主要为第四系下更新二期冰碛层为主的地质结构。 由地层勘探结果可知,隧道上覆岩层自上而下可分为:①砾砂土层,厚度约10 m;②中、强风化玄武岩,土层厚40 m左右;③地表埋深50 m 以下围岩以冰碛层为主,其内部以冰川融水为主要应力,旁侧含透水岩层。 主隧道K2 +234.00~+139.00 m 段围岩节理裂隙发育较好,岩体整体较为破碎,沿断裂带形成构造裂隙透水通道,汇集较丰富的地下水,成为富水性良好的含水层。 主隧道K2 +234.00~+139.00 m 段地层结构如图1 所示。

图1 地层结构示意图
2 数值模拟分析
台阶法按步距不同可划分为长台阶法、短台阶法以及微台阶法。 为研究不同开挖方式对隧道稳定性的影响,分别模拟不同台阶长度条件下隧道开挖过程,根据施工后渗流场、应力场、位移场以及塑性区状况评估施工效果。
2.1 三维数字模型
根据小麻柳尾矿库主隧道K2 +234.00~+139.00 m段地形情况及图1 构建三维数字模型,为降低边界效应对模拟结果的影响,考虑圣维南原理,模型左右侧及底部均取5 倍开挖尺寸,开挖长度约95 m,整个模型尺寸为66 m×95 m×130 m,模型单元和节点数分别为482 605 和265 493。 模型示意图见图2。
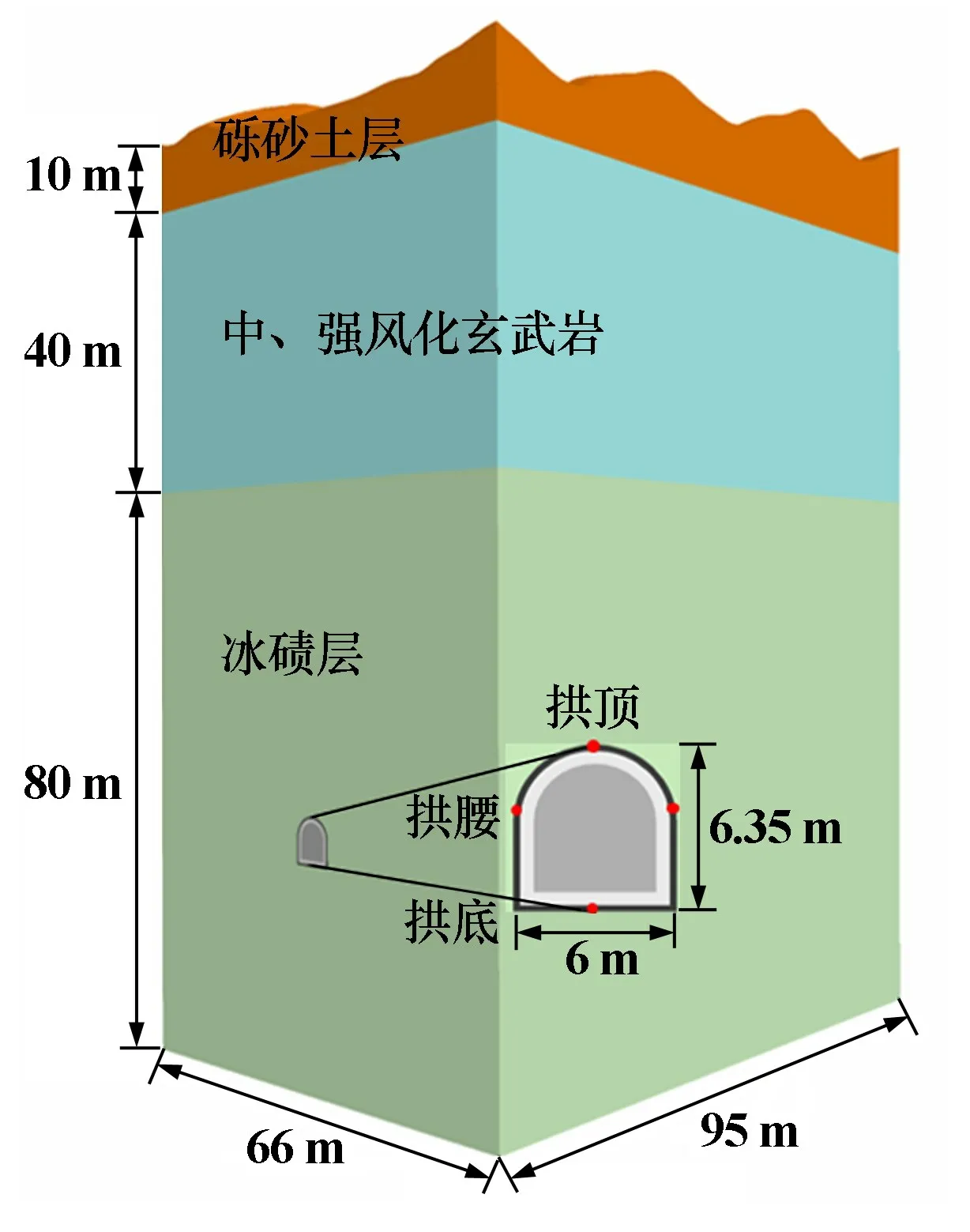
图2 模型示意图
2.2 边界条件及材料参数
根据工程实际情况,对各土层参数赋予摩尔-库伦本构模型,忽略土体断层影响,隧道开挖后以锚网喷砼+锚杆进行初期支护,分别以弹性本构模型及锚结构单元进行模拟,二次衬砌支护以弹性本构模型进行模拟。各土层结构中,中、强风化玄武岩及冰碛层为导水土层,其中冰碛层内汇聚较丰富地下水,以各向同性流体材料进行模拟。 静力学边界条件为四周法相位移约束、底部位移全约束、顶部为自由面;渗流场边界条件为四周及底部边界均为不透水边界,顶面无水,初期支护及二次衬砌支护均为不透水材料,开挖面处自然排水。
为合理确定围岩力学参数,提高数值模拟结果准确性,从施工现场进行取样,将其加工打磨成标准试样进行三轴及直剪等试验,测定围岩及支护材料力学参数,结果见表1。
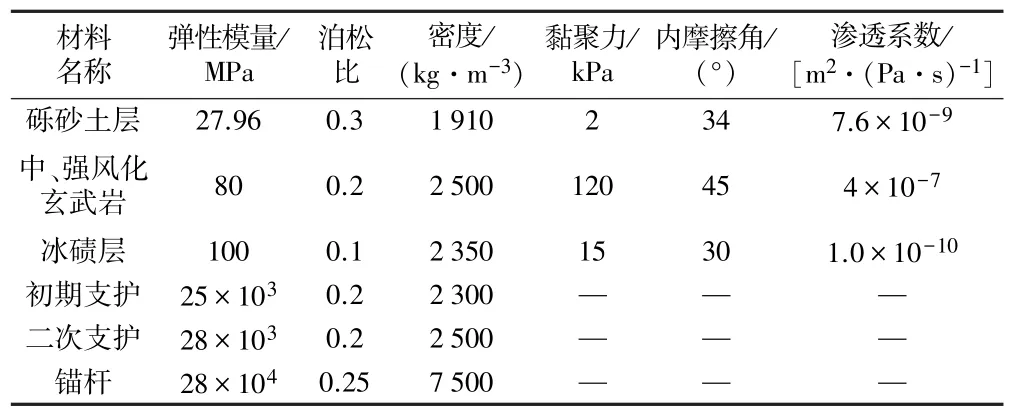
表1 围岩及支护结构材料参数
2.3 模拟施工步骤
模型开挖方式为上下台阶法,开挖循环为5 m,单次施工前需进行排水处理,进行自然渗流,渗流时间为12 h;排水完毕后进行施工,开挖后即刻进行锚网喷砼+锚杆初期支护,喷砼厚度0.25 m,锚杆长度3 m,直墙隧道上部锚杆间距0.85 m、下部锚杆间距1.0 m;待初期开挖支护应力平衡后,再进行下一循环施工作业,二次衬砌支护滞后4 个开挖循环,二次衬砌支护厚度0.5 m。
根据台阶法划分标准,结合隧道面开挖尺寸,分别模拟不同台阶条件下施工过程,其中长台阶法台阶长度为5 倍开挖尺寸(即30 m),短台阶法台阶长度为1.67 倍开挖尺寸(即10 m),微台阶法台阶长度为0.83倍开挖尺寸(即5 m)。
3 模拟结果分析
3.1 渗流场分析
图3 为不同台阶长度施工后冰碛层渗流场分布情况。
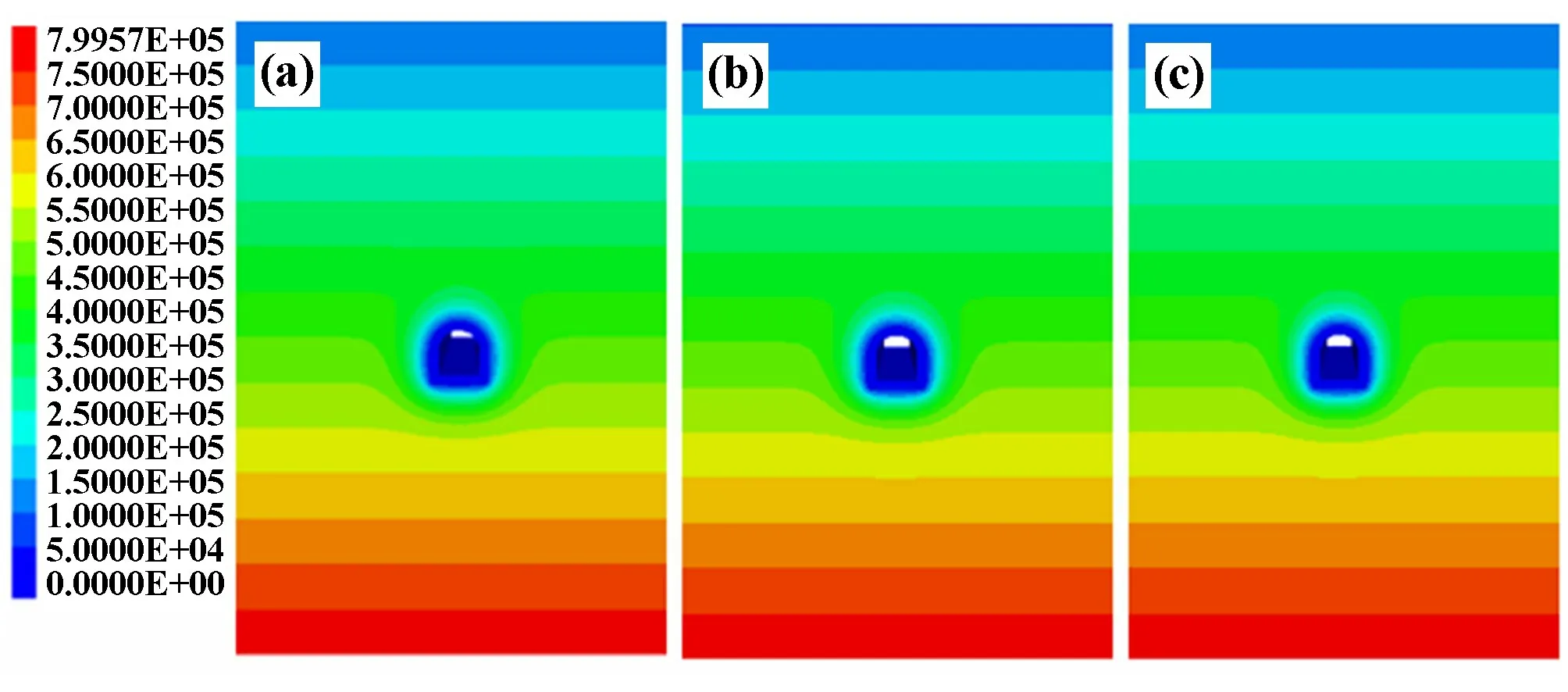
图3 渗流场分布示意图
长台阶法、短台阶法以及微台阶法仅开挖步距不同,开挖循环次数一致,且在每次开挖前都先进行排水处理,排水时间均为12 h,故三类施工方法渗流场分布形式类似,与图3 结果一致。 从图3 可知,富水隧道开挖区域孔隙水压力有所降低,孔隙水压力等值线成漏斗形状。 因此,在施工前对开挖区域提前进行排水处理,能够一定程度降低孔隙潜水对施工作业的影响,提高施工作业效率及安全性。
3.2 位移场分析
图4 为三类施工方法隧道附近围岩合位移云图。
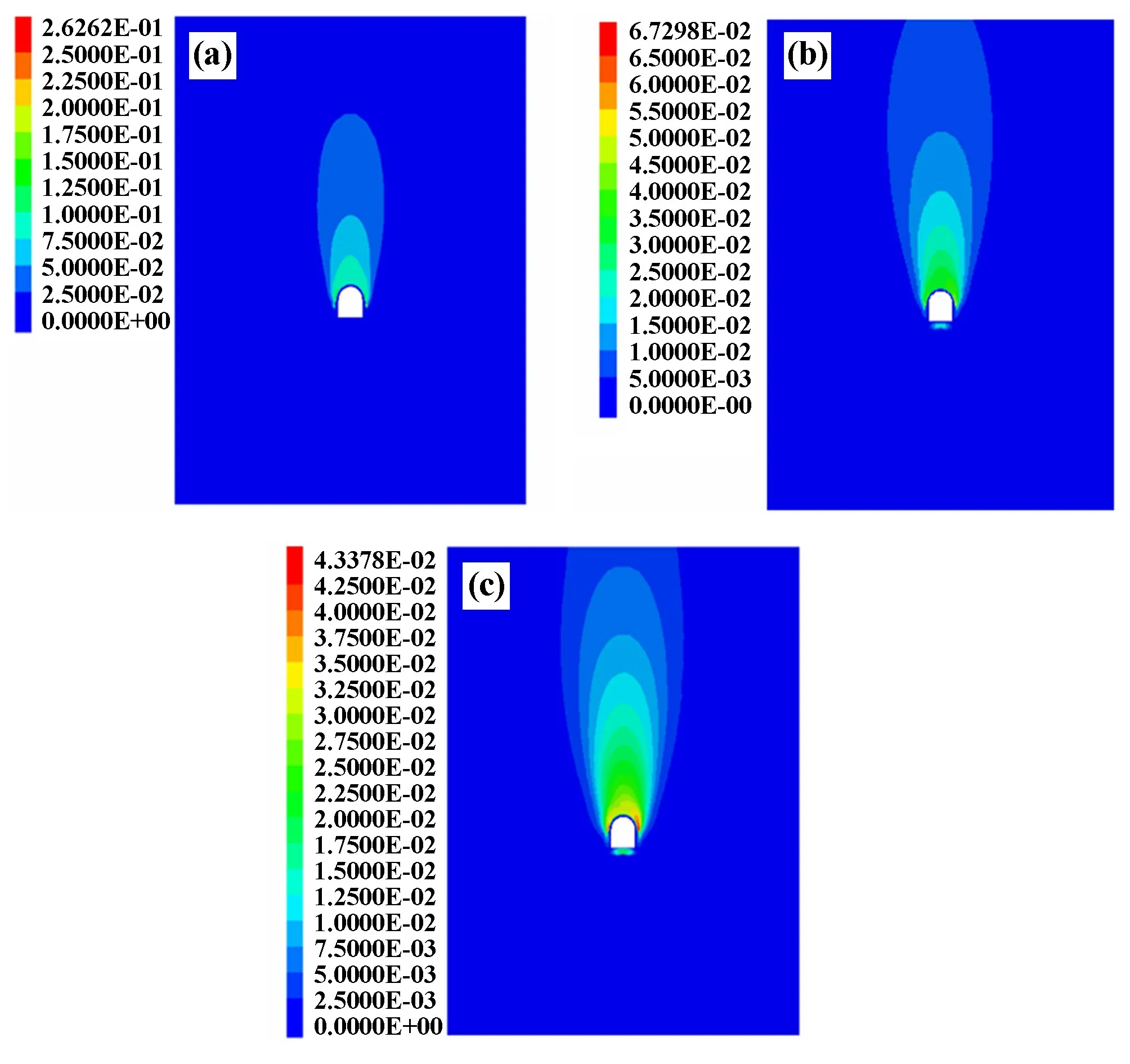
图4 围岩合位移云图
由图4 可知,富水隧道开挖后拱底位移较小,围岩变形主要集中在拱顶及拱腰处。 由掌子面附近位移分布情况可知,添加二次衬砌后,二次衬砌区域合位移明显降低,位移数值均小于0.05 m。 对比三类施工方式合位移数值大小可知,长台阶法施工在初期支护拱腰处合位移最大,达到0.263 m,短台阶法合位移最大处同样位于初期支护拱腰处,数值为0.067 3 m,微台阶法施工合位移最大值为0.043 4 m。
为细化分析隧道竖向位移及侧向位移分布情况,监测沿开挖方向拱顶、拱底竖向位移及拱腰两侧侧向位移,图5 为监测数据图(其中拱顶及右拱腰数据取绝对值)。

图5 施工位移监测数据
从图5 可知,三类方法施工隧道拱顶处位移数值较大,其次为拱腰处,拱底位移最小,与图4 结果一致。同时,分析各类施工方法位移数据变化趋势可知,位移大体呈周期变化规律,结合施工模拟过程可得,位移变化周期与锚杆间隔大体一致,由此可知锚杆对围岩加固作用明显,施工后及时进行锚杆支护可有效降低施工作业区域围岩变形。 此外,分析施工位移数据可得,隧道左右拱腰处监测点位移变化趋势有所差异,主要原因在于隧道左右拱腰处监测点距地表土层深度存在差异,且由于长台阶法及短台阶法施工时上下台阶施工间隔较长,拱腰处应力释放较为充分,左右拱腰处位移监测曲线差异较大,微台阶法上下台阶施工循环间隔较小,应力释放较为缓慢,左右拱腰处位移监测数据相差较小。
由图5 可知,三类施工方法中,长台阶法拱顶位移明显高于拱腰及拱底,主要原因在于长台阶法施工过程中,台阶步距较长,上台阶开挖后应力释放充分,所产生拱顶位移较大,最大位移值为0.09 m。 分析长台阶法位移总体变化趋势可得,沿开挖深度方向大于上台阶开挖步距30 m 时,隧道底部下台阶开始施工,施工作业区域增大,隧道拱顶处位移也逐渐开始增加。 短台阶法施工台阶步距较短,隧道拱顶位移与拱腰及拱底位移差异较小,沿开挖深度方向超过开挖步距10 m 时,开挖面增大,隧道周边围岩变形随之增加,拱顶最大沉降为0.05 m。 微台阶法由于超前步距最小,施工作业对围岩影响最小,拱顶位移与拱腰、拱底位移数据相近,拱顶沉降最大值位于洞口处,最大值为0.028 2 m。
3.3 应力场分析
图6 为施工后监测点应力数据图(拱顶数据取绝对值)。
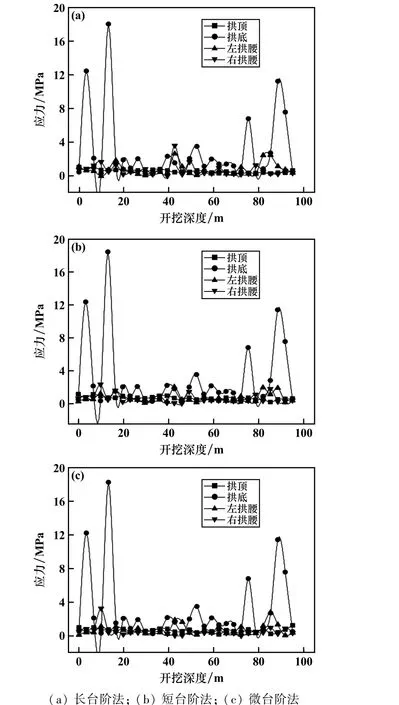
图6 施工应力监测数据
从图6 可知,三类台阶法施工应力分布形式类似,拱顶及拱腰应力监测数据较小,不超过4 MPa,拱底应力较大,应力最大值超过18 MPa,且在隧道洞口段及出口段应力值较大,隧道中间部分应力值较小。 由工程实际情况可知,隧道埋深约100 m,埋深较浅,施工作业区域竖向应力较大、侧向应力较小,拱腰处应力数据较小。 采用台阶法开挖,由于上台阶隧道超前作业,应力释放较为充分,拱顶处监测应力数据较小,下台阶滞后开挖应力较为集中,拱底处应力值较大。 受边界条件影响,隧道在洞口段及出口段应力较为集中,施工至隧道出口段时部分应力已释放,隧道出口段拱底应力监测值小于隧道洞口段应力值。
3.4 塑性区分析
图7 为三类台阶法施工作业后塑性区分布情况。
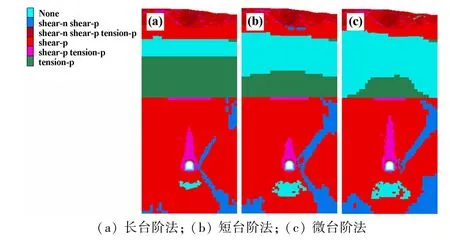
图7 塑性区分布示意图
由图7 可得,三类施工方式塑性区分布状况类似,在隧道右侧区域均产生了剪切破坏区域。 分析可知,施工作业区域隧道左右侧围岩埋深存在差异,结合图5,隧道右拱腰处位移变形量较大,在隧道右侧围岩区域会形成剪切破坏区域。 相较于长台阶法,短台阶法以及微台阶法上下台阶循环间隔较小,应力释放不够充分,故会形成更多的剪切破坏区。
4 台阶法施工效果综合分析
综合各台阶法施工作业后位移场、应力场及塑性区等因素影响,以竖向位移、侧向位移、竖向应力、侧向应力、剪切破坏区以及拉伸破坏区体积等因素作为评价指标,以CRITIC 算法计算上述各因素指标权重。表2 为各施工方案初始数据。

表2 各施工方案初始评价数据
分析可知,三类台阶法施工后渗流场及应力场分析形式相似,其中微台阶法施工后隧道附近围岩变形较小,但隧道右侧产生了较大的剪切破坏区。
由于各评价指标因素量纲存在差异,为消除量纲影响,需对数据进行归一化处理。 表3 为表2 数据归一化处理后各评价指标数据。 根据归一化数据,采用CRITIC 算法对其进行分析,计算各因素评价指标权重,结果见表4。
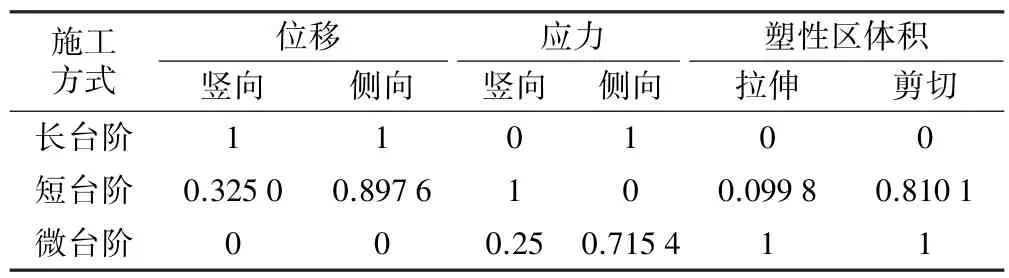
表3 评价指标归一化数据
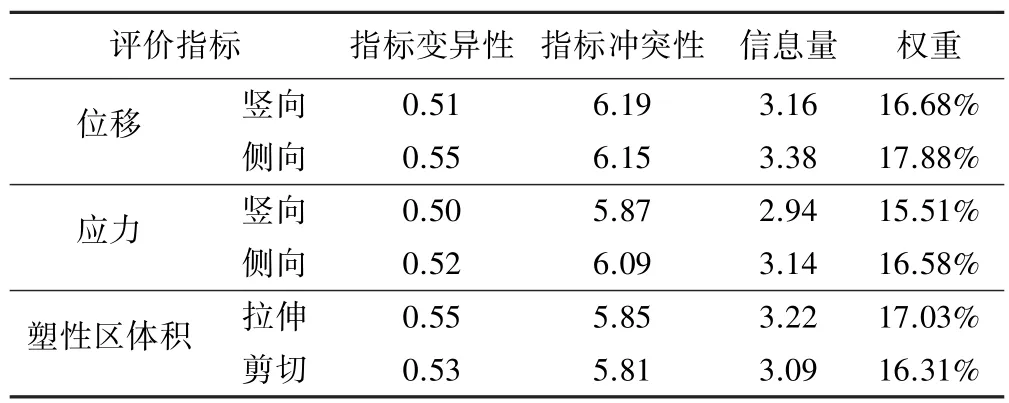
表4 评价指标权重计算结果
由表3 及表4 可分别计算三类台阶法施工方案综合得分。 上述评价指标均为逆向指标,综合评分越低,表明该类施工方案适用性越高。 根据各指标权重数据,计算各方案指标数据与权重乘积,并加以求和,长台阶法、短台阶法以及微台阶法综合得分分别为:0.511 4,0.518 9,0.490 8。 在上述三类施工方案中,微台阶法最适于此条件下隧道施工;其次为长台阶法,长台阶法施工隧道能够使围岩应力得到较为充分释放,所产生塑性区较小;短台阶法施工效果较差,施工后竖向应力较大,且施工后塑性区体积较大。
按上述分析结果指导实际施工过程,实际施工过程中采用微台阶法施工隧道,支护方式采用锚网喷砼+锚杆进行初期支护,衬砌进行二次支护。 隧道施工后监测隧道顶部及底部围岩变形,拱顶沉降和拱底隆起值分别约3 cm 和2 cm,与上述模拟结果大致相同,满足施工要求。
5 结 论
以小麻柳尾矿库主隧道工程为例,选取主隧道K2+234.00 ~+139.00 m 段为研究对象,结合工程实测数据资料,采用FLAC3D分别模拟了富水条件下不同台阶步距开挖过程,分析了隧道施工作业后渗流场、位移场、应力场及塑性区分布情况,在此基础上进行综合分析评价,得到适于富水隧道施工方法,具体结论为:
1) 支护作业能有效降低围岩变形。 由隧道监测点位移数据可知,锚杆支护对隧道周边围岩变形有较大影响,其位移变化循环周期与锚杆间隔周期一致。由隧道位移云图可知,二次衬砌支护区域变形量较小,均小于0.025 m。 因此在实际施工过程中,可通过提高锚杆数量、进行二次衬砌支护等方式降低隧道围岩变形。
2) 隧道开挖两侧地表高程变化显著时,隧道开挖两侧应力存在差异,采用对称式支护方式时,在埋深较高一侧易产生应力集中,造成较大区域剪切破坏区域,故对偏压隧道进行施工时应采取对应措施减少对高应力侧围岩的扰动。
3) 富水条件下隧道施工过程中,长台阶法产生位移较大,但由于上台阶超前开挖循环较长,应力释放较为充分,拱顶及拱底应力值较小,拱腰侧应力值较大,产生塑性区体积较小;短台阶法施工位移较小,侧向应力也相对较小,但拱顶处应力较大,塑性区体积也较大;微台阶法施工隧道附近位移最小,但侧向应力较大,在侧向应力集中区域产生了较大剪切破坏区域。综合多方面因素分析,微台阶法最适于富水条件下隧道施工,其次为长台阶法,短台阶法施工效果较差。
