中国盘腹蚁属19 种蚂蚁的形态测量学研究

段加焕，徐正会，张新民

(西南林业大学生物多样性保护学院，云南省森林灾害预警与控制重点实验室，云南 昆明 650224)

蚂蚁是陆地上最常见的昆虫，也是评价生态环境质量和生物多样性的重要指示生物[1]。目前全世界已记载16 亚科346 属14 110 种[2]。随着研究的不断深入，种类不断增加，研究学科和方向也不断扩展，可横跨分类学、生态学和生物学等[3]。蚂蚁具有重要的生态和经济价值，在生态系统中占据着重要的位置，但有些蚂蚁也会带来危害，例如入侵性的蚂蚁会占领、破坏入侵地的生态环境和资源，有些则可能传播病毒或通过取食植物根茎造成经济损失[1,4-5]。近年来，国内学者对蚂蚁的研究取得了很大的进步，尤其在分类、多样性和分布格局等方面[6-13]，但总体来说与西方发达国家还有一定的差距，有待进一步深入研究。

盘腹蚁属（AphaenogasterMayr），隶属于膜翅目（Hymenoptera）、蚁科（Formincidae）、切叶蚁亚科（Myrmicinae）[14]，于1853 年由科学家Mayr 建立。截至目前，盘腹蚁属全世界有效命名206 种[1]，国内记录31 种[15]。该属已知的大多数物种主要来自北半球，以古北区最多，东洋区次之[16-19]，许多种类均是落叶林和针叶林中的常见种或优势种[19-20]。

形态测量学（morphometrics）是对某一性状定量描述和分析的一种统计研究方法。该方法能够定量表现昆虫的某些特征值，利用因子分析、主成分分析和聚类分析等相结合的统计学方法，对物种进行分类和系统发育分析。例如谷博[21]、黄海燕[22-23]、张荣娇[24]、Weiseri & Kaspari[25]、Hazarika[26]和Samung[27]等利用形态测量学方法对蚁科昆虫进行了研究，发现该方法有助于厘定已知的蚂蚁种类及有效分区形态相似的物种。Csősz 等用分子系统学和形态测量学方法对盘腹蚁属A.swammerdami组群进行分析，基于系统聚类将该组群聚划分成5 组，并发表了3 个新种[28]。由此可见，形态测量学方法在蚁科昆虫的分类中具有重要价值。

本研究以分布于中国的19 种盘腹蚁属蚂蚁作为研究材料，选取14 个形态特征为变量，通过因子分析、主成分分析和聚类分析，对该类群进行了形态测量学研究，区分近缘种类，以期为该属蚂蚁的分类提供新的信息。

1 材料与方法

1.1 研究材料

研究材料来源于本文作者采集的标本和实验室多年积累的标本，所有实验标本均收藏于西南林业大学标本馆。

1.2 研究方法

1.2.1 标本的采集及制作 所用的蚂蚁标本是前期研究时通过样地调查法和搜索调查法采集[1,29]，采集时标本储存于装有无水乙醇的2 mL 冻存管内。之后通过清洗标本→初步分类→显微镜下初步整姿→用中性树胶粘在三角纸上→再次调整蚂蚁姿态→书写标签等步骤，将其制作成针插标本，备用。

1.2.2 形态测量 蚂蚁标本的测量使用SOPTOP SZM 连续变倍体视显微镜。具体步骤：打开显微镜，旋转目镜使测微尺水平→调节最合适的倍数→将标本插于泡沫纸板→显微镜下观察，移动泡沫板，使测量部位与目镜测微尺在同一水平面→读出测量数值→记录。为减少实验测量误差，每个形态特征值重复测量3 次后取平均值，精确度为0.01 mm。以此方法测量盘腹蚁属19 种蚂蚁14 个形态特征值，每个物种各测量5 头标本。14 个形态特征分别为体长（TL）、头长（HL）、头宽（HW）、触角柄节长（SL）、前胸背板宽（PW）、胸长（MSL）、腹柄宽（DPW）、腹柄长（PL）、腹柄高（PH）、头比（CI）、触角柄节比（SI1）、触角柄节比（SI2）、腹柄长宽比（LPI）和腹柄长高比（DPI），测量内容以及标准参考了Borowiec &Salata[30]、Salata & Borowiec[31]，Salata 等[18]以及Csősz 等[28]等（表1）。

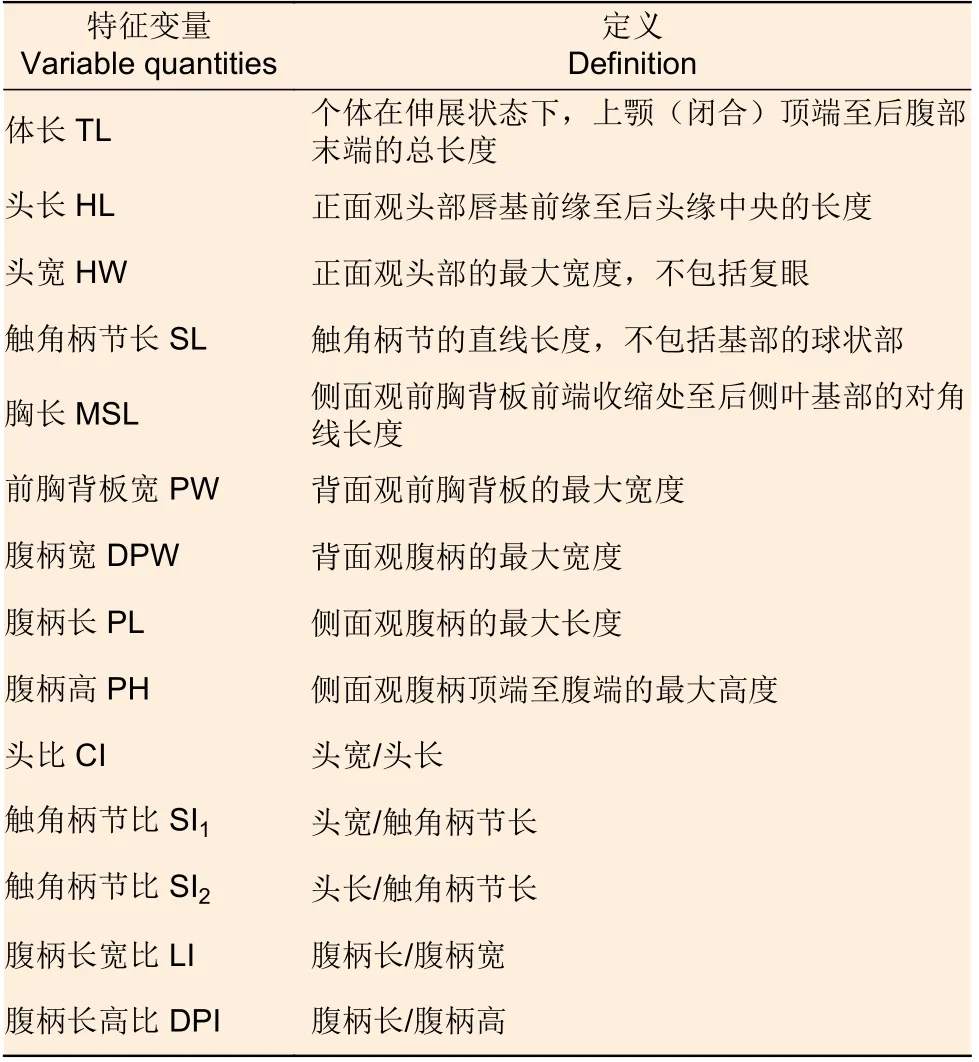
表1 盘腹蚁属蚂蚁的14 种性状Table 1 Measured 14 morphological characters of the genus Aphaenogaster

1.2.3 原始数据标准化 为了消除数据单位不同、自身变异或数值相差较大所造成的影响，使用SPSS 26.0 软件将原始数据进行标准化处理，得到无单位的矩阵。

1.2.4 数据分析方法 因子分析：将具有一定相关关系的多个变量综合为几个因子，是一种处理多变量问题的常用统计方法[21]。以每个变量作为一个因子，运用SPSS 26.0 软件以“降维”的模式进行因子分析。

主成分分析：在不丢失大量信息的前提下，利用多个变量之间的相关性，通过降维技术，用少数的变量来代替多个变量的统计分析方法[32]。当因子间具备一定相关性时，通过研究众多因子之间的内部依赖关系，提取主成分，运用SPSS 26.0 软件以主成分的因子得分制作三维散点图。

系统聚类分析：按照一定的数据连接规则和一定的层次结构将数据聚合，形成一个层次的聚类，从而辨别各种群之间的亲疏关系[33]。本文选择SPSS 26.0 软件中的系统聚类方法，以平方欧氏距离为距离度量，选择离差平方和为法聚类规则，得出19 种盘腹蚁属蚂蚁的系统聚类树状图。

2 结果与分析

2.1 测量结果

将盘腹蚁属19 种蚂蚁标本的14 个形态特征测量结果用Excel 进行处理（n=5），取每种蚂蚁各性状的平均值（表2）。

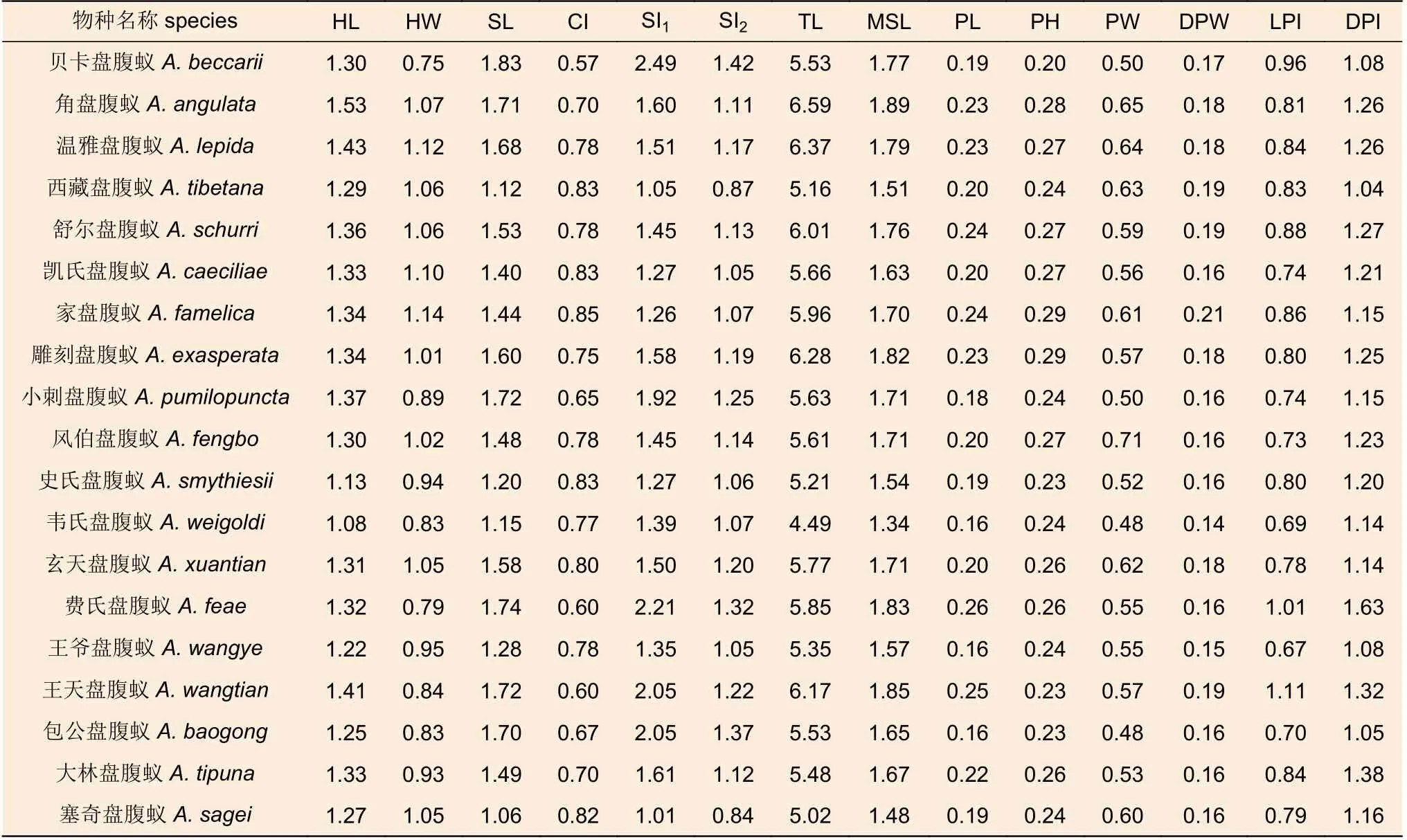
表2 盘腹蚁属19 种蚂蚁的14 个形态特征值的平均值Table 2 The average value of 14 morphological characteristics of 19 species of the genus Aphaenogaster

2.2 原始数据标准化

将盘腹蚁属19 种蚂蚁的14 个形态特征值的平均值运用SPSS 26.0 软件进行标准化处理的结果（表3）。

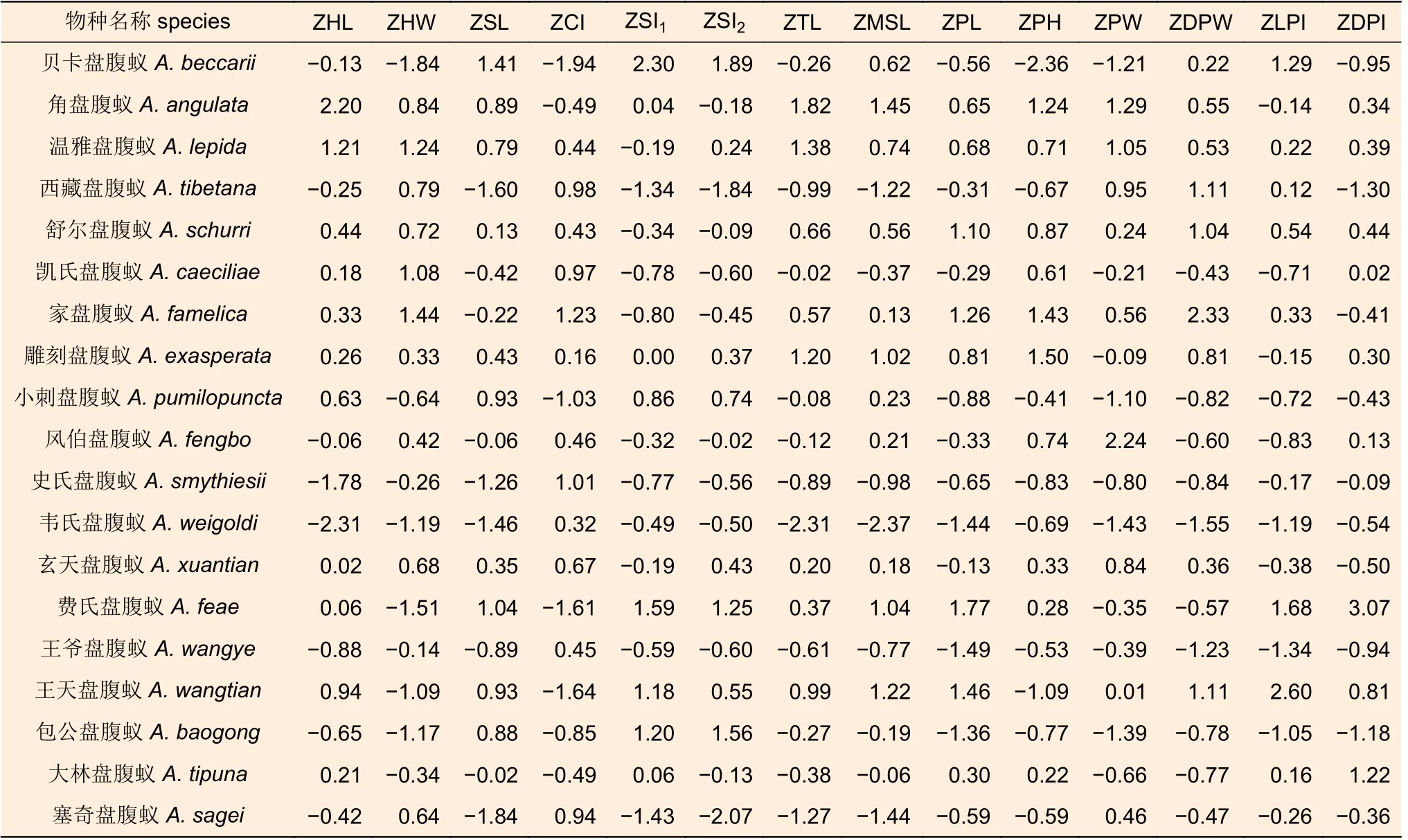
表3 盘腹蚁属19 种蚂蚁的14 个形态特征值的平均值标准化处理结果Table 3 The average of standardized results from14 morphological characteristic values in the 19 studied Aphaenogaster species

2.3 因子分析

选取盘腹蚁属19 种蚂蚁的14 个形态特征为变量，运用SPSS 26.0 软件进行因子分析（表4～6）。

表4 KMO 和Bartlett 检验Table 4 KMO and Bartlett's Test

KMO（Kaiser-Meyer-Olkin）检验统计量可以检验各个变量是否各自独立。由表4 可知，KMO=0.61＞0.6 时，原有变量满足因子分析的前提条件，说明可做因子分析。Bartlett's 球状检验结果显示：显著性=0＜0.05，说明各变量间具有很强的相关性，因子分析有效。

第1 主成分、第2 主成分、第3 主成分和第4 主成分的特征值分别为：6.14、4.52、1.28、1.04，这4 个成分各自累计值都超过1，其余成分的累计值都远小于1，有的成分累计值接近或等于1；第1 主成分、第2 主成分、第3 主成分和第4 主成分的贡献率分别为43.84%，32.35%、9.14%、7.43%；这4 个成分累积贡献率达到92.76%，因子分析效果理想（表5）。由此可见，抽取这4 个成分可以综合反映14 个形态特征值，能够涵盖大多数变量的基本信息，同时也可分析得到4 个主成分的因子负荷值（表5）。

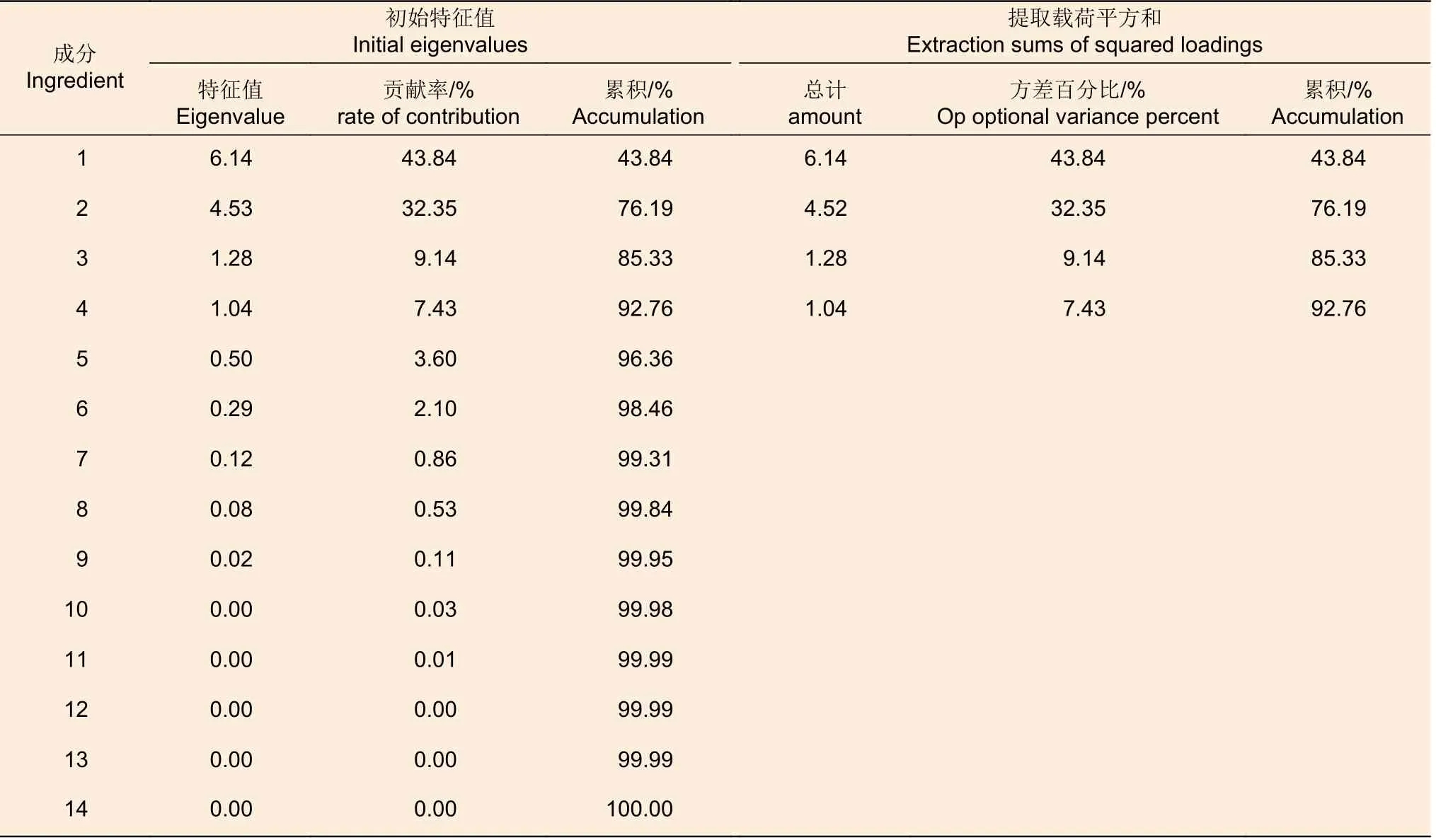
表5 盘腹蚁属19 种蚂蚁的14 个形态特征值的总方差解释Table 5 Interpretation of the total variance of 14 morphological characteristic values of 19 species of the genus Aphaenogaster

由表6 可知，盘腹蚁属19 种蚂蚁中第1 主成分的负荷值较第2 主成分、第3 主成分和第4 主成分大，且第1 主成分各变量间负荷值大多相差较大，少部分变量间负荷值相差较小，说明第1 主成分能够较好的反应14 个形态特征值，但并不能反应全部形态特征值，有必要进行进一步的分析。在第1 主成分、第2 主成分、第3 主成分和第4 主成分中，具有最大因子负荷值的性状分别是胸长（MSL）、头宽（HW）、腹柄长宽比（LPI）和腹柄长高比 （DPI），所以第1 主成分、第2 主成分、第3 主成分和第4 主成分分别由胸长（MSL）、头宽（HW）、腹柄长宽比（LPI）和腹柄长高比 （DPI），同时，由于腹柄长宽比（LPI）是腹柄长（PL）与腹柄宽（DPW）的比值，所以第3 主成分在一定程度上间接受到了腹柄长（PL）与腹柄宽（DPW）的影响，同理，第4 主成分受到了腹柄长（PL）与腹柄高（PH）的影响。

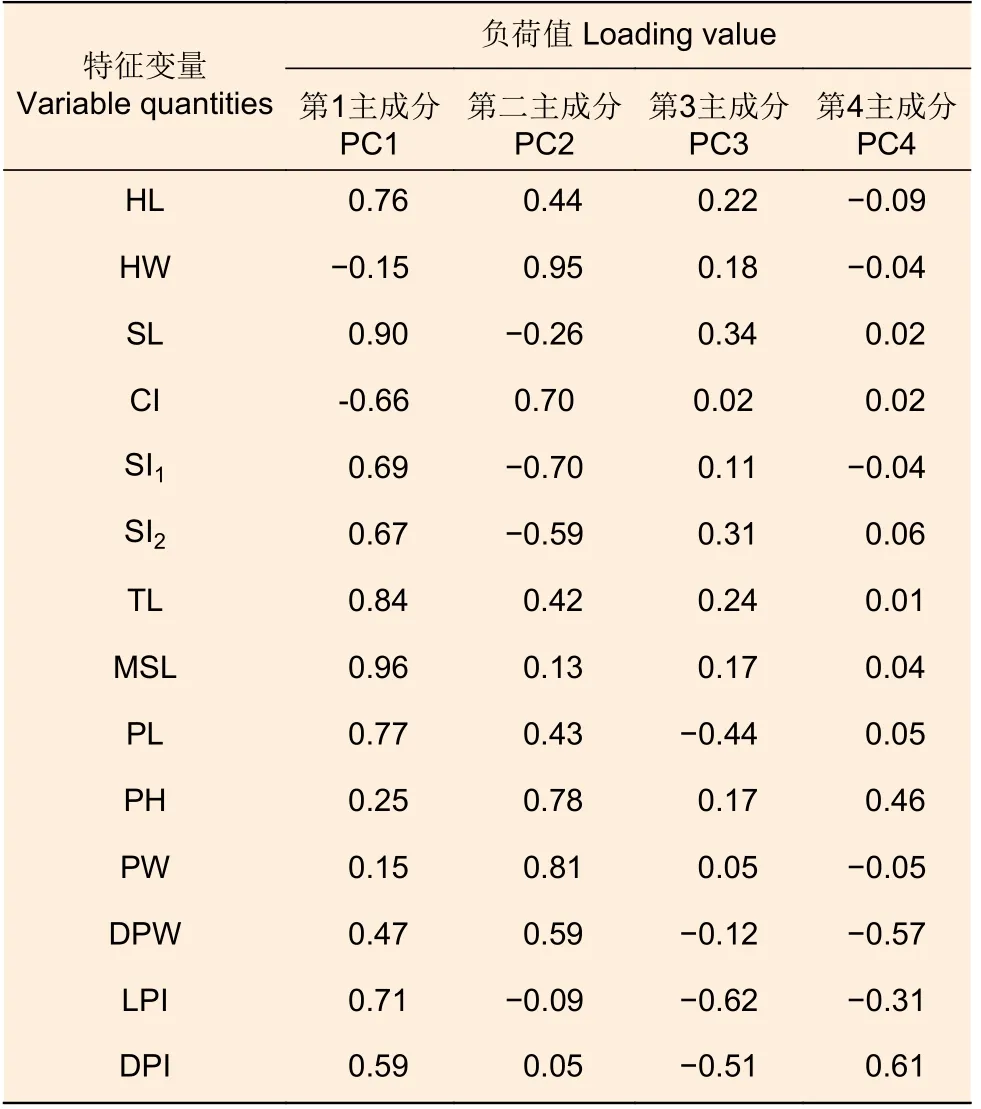
表6 盘腹蚁属19 种蚂蚁的形态特征主成分负荷值Table 6 Loading of principal components on the morphological characteristics of 19 species of the genus Aphaenogaster

2.4 主成分分析

根据因子分析结果，计算主成分特征向量负荷值，然后根据主成分特征向量负荷值计算（表7）4 个主成分的得分，表达式中Z 表示标准化后的变量。主成分的表达式如下：

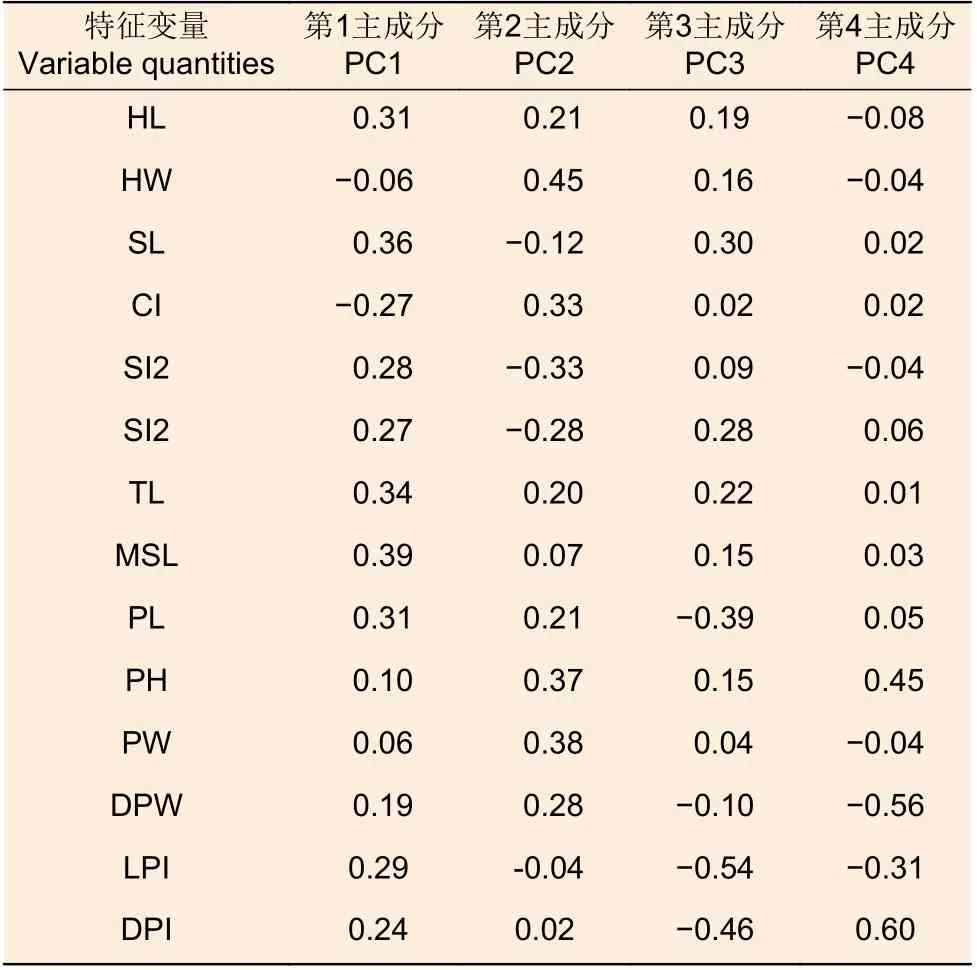
表7 特征向量矩阵Table 7 The matrix of feature vector

Y1=0.31×ZHL - 0.06×ZHW + 0.36×ZSL -0.27×ZCI + 0.28×ZSI1+ 0.27×ZSI2+ 0.34×TL +0.39×ZMSL + 0.31×ZPL + 0.10×ZPH + 0.06×ZPW +0.19×ZDPW + 0.29×ZLPI + 0.24×ZDPI

Y2=0.21×ZHL + 0.45×ZHW - 0.12×ZSL +0.33×ZCI - 0.33×ZSI1- 0.28×ZSI2+ 0.20×TL +0.07×ZMSL + 0.21×ZPL + 0.37×ZPH + 0.38×ZPW +0.28×ZDPW - 0.04×ZLPI + 0.02×ZDPI

Y3=0.19×ZHL + 0.16×ZHW + 0.30×ZSL +0.02×ZCI + 0.09×ZSI1+ 0.28×ZSI2+ 0.22×TL +0.15×ZMSL - 0.39×ZPL + 0.15×ZPH + 0.04×ZPW -0.10×ZDPW - 0.54×ZLPI - 0.46×ZDPI

Y4= - 0.08×ZHL - 0.04×ZHW + 0.02×ZSL +0.02×ZCI - 0.04×ZSI1+ 0.06×ZSI2+ 0.01×TL +0.03×ZMSL + 0.05×ZPL + 0.45×ZPH - 0.04×ZPW -0.56×ZDPW - 0.31×ZLPI + 0.60×DPI

在上述表达式中各变量是标准化变量，负荷值的绝对值越大，贡献也就越大；根据表7，结合主成分的表达式可得到19 种蚂蚁4 个主成分的得分。

胸长（MSL）、头宽（HW）、腹柄长宽比（LPI）和腹柄长高比 （DPI）是主要性状。此外，柄节长（SL）、柄节比（SI1）和腹柄高（PH）3 个性状对数据有着间接的影响。这7 个性状基本涵盖了所涉及的14 个性状特征，利用上述主要性状能够明显区分19 种蚂蚁。由于第1 主成分、第2 主成分、第3 主成分的累积贡献率为85.33%，超过了85%，且第4 主成分形态特征负荷值大多小于0.1，所以本文选取了1 主成分、第2 主成分、第3 主成分的因子得分数据制作三维散点图（图1）。

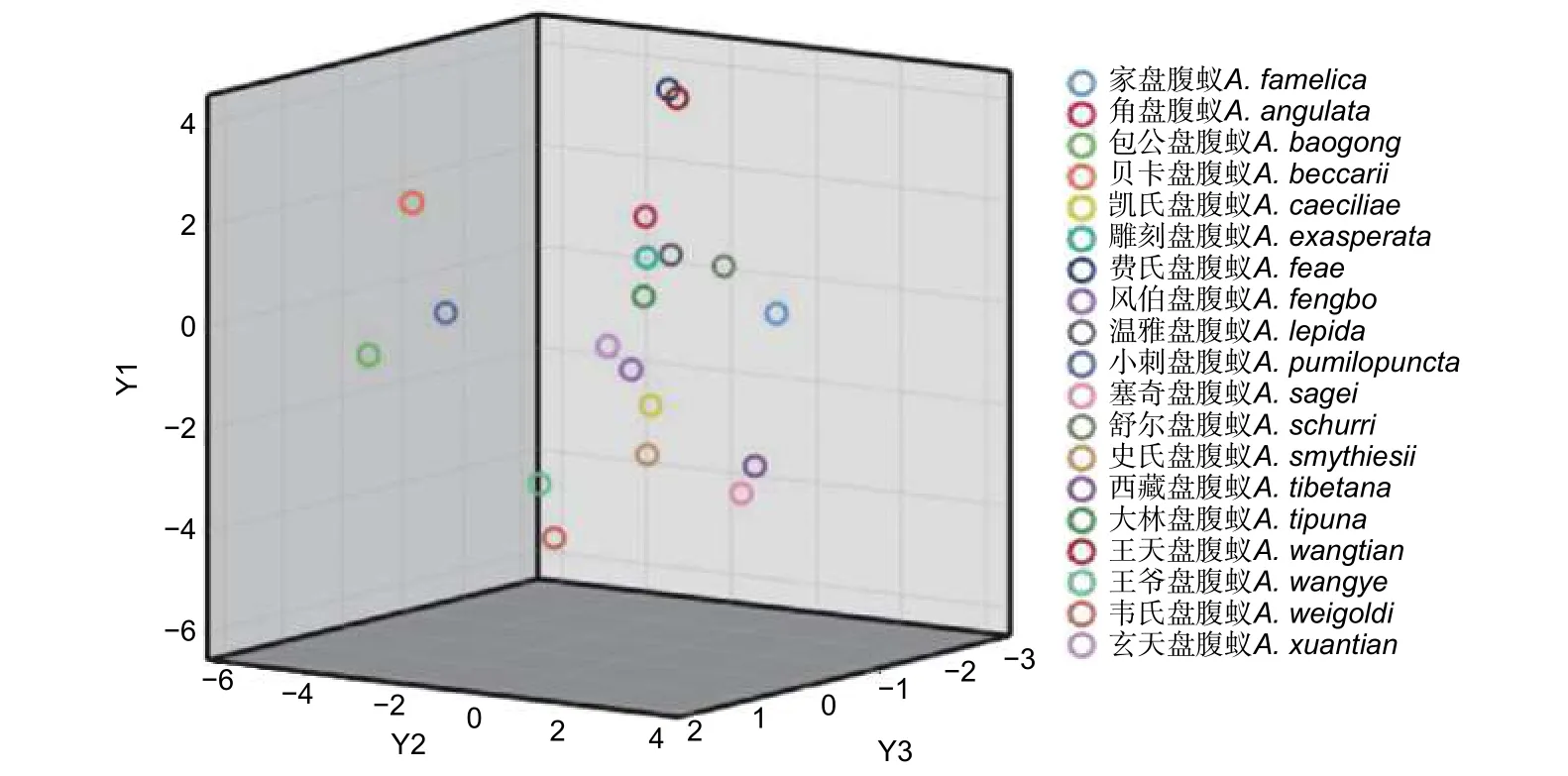
图1 盘腹蚁属19 种蚂蚁形态测量学主成分得分三维散点图Fig.1 Three-dimensional scatter plot of principal component scores of 19 species of the genus of Aphaenogaster

从主成分的三维散点分布图（图1）可以看出，以第1 主成分、第2 主成分和第3 主成分构成的散点图能够较明显区分盘腹蚁属19 种蚂蚁，但费氏盘腹蚁和王天盘腹蚁存在重叠现象；包公盘腹蚁、贝卡盘腹蚁和小刺盘腹与其他几组分开最远。此外，散点图总体表现为形态相似的物种其散点分布是相互靠近的，而那些形态相差较大的物种，其散点分布也呈现出不同程度的远离。由此可见，以3 个主成分做出的散点图能够将19 种蚂蚁区分开。

2.5 系统聚类分析

基于欧式距离，利用SPSS 26.0 软件，以14 个性状为变量，对盘腹蚁属19 种蚂蚁进行系统聚类分析。由图2 可知，以20 为标度将盘腹蚁属19 种蚂蚁聚成了2 个大支。费氏盘腹蚁、王天盘腹蚁、包公盘腹蚁、贝卡盘腹蚁和小刺盘腹蚁聚成1 支，其余14 种聚成1 支。以15 为标度则被聚成了4 支。第一支有舒尔盘腹蚁、雕刻盘腹蚁和角盘腹蚁等9 个种；第二支有5 种，分别为史氏盘腹蚁、韦氏盘腹蚁、王爷盘腹蚁、塞奇盘腹蚁和西藏盘腹蚁；第三支只有费氏盘腹蚁和王天盘腹蚁两种；第四支有包公盘腹蚁、贝卡盘腹蚁和小刺盘腹蚁3 种。根据系统聚类树状图中的种间距离判断彼此间的亲缘关系得出：第一支与第二支的相似度最高，亲缘关系最近；与第三支的相似度次之，亲缘关系较远；与第四支的相似度最低，亲缘关系最远。同理，第三和第四支之间的亲缘关系最近。各支种间相似度最高，亲缘关系最近，与其他支的物种亲缘关系最远。结果表明：形态特征相似的种类会聚到一起，距离越近，亲缘关系越近。

图2 盘腹蚁属19 种蚂蚁系统聚类Fig.2 Systematic clustering of 19 species of the genus of Aphaenogaster

3 讨论

本文选取19 种盘腹蚁的14 个形态特征值作为变量，通过因子分析和主成分分析，抽取了胸长（MSL）、头宽（HW）、腹柄长宽比（LPI）和腹柄长高比 （DPI）4 个成分进行综合分析，4 个主成分累积贡献率达到了92.76%，说明因子分析效果明显。而张荣娇在研究厚结猛蚁属13 种的时候，抽取的主成分是头长（HL），头宽（HW），头比（CI），触角柄节比（SI）[24]；谷博在中国蚁亚科形态测量学研究中抽取的主成分为体长（TL）、触角柄节比（SI）、前胸比（PI）[21]。不同类群的蚂蚁由于形态特征、栖息生境等方面存在较大差异，导致了不同类群分类由不同的性状特征所决定。虽然各类群所抽取的主成分不同，但均可以实现区分物种的目的，因此我们认为形态测量学的研究在物种分类方面具有一定的价值，可以在其它类群间推广应用。

盘腹蚁属19 种蚂蚁系统聚类结果与主成分得分散点图结果基本一致，与传统的形态分类的结果大致吻合。根据系统聚类结果费氏盘腹蚁、王天盘腹蚁、包公盘腹蚁、贝卡盘腹蚁和小刺盘腹蚁5 种头在复眼后明显收缩延伸的物种，具有更近的亲缘关系，这与传统形态分类结果十分符合；温雅盘腹蚁和角盘腹蚁以及西藏盘腹蚁和塞奇盘腹蚁等在形态特征上较相似的物种，在系统聚类结果和主成分得分散点图上也均表现出较近的亲缘关系，且散点图上它们均未出现重叠现象，由此可见，形态测量方法物种分类、区分相似种、研究物种间亲缘关系等方面具有一定价值。系统聚类结果中史氏盘腹蚁和王爷盘腹蚁的亲缘关系要比王爷盘腹蚁和韦氏盘腹蚁更近，而在散点图中，史氏盘腹蚁距离王爷盘腹蚁和韦氏盘腹蚁要更远，与系统聚类结果存在微小差异；同样，大林盘腹蚁在系统聚类中的亲缘关系与凯氏盘腹蚁、风伯盘腹蚁和玄天盘腹蚁要比家盘腹蚁、角盘腹蚁、温雅盘腹蚁和雕刻盘腹蚁更近，在散点图中，大林盘腹蚁与角盘腹蚁、温雅盘腹蚁和雕刻盘腹蚁的距离比较接近，没有显示出与凯氏盘腹蚁、风伯盘腹蚁和玄天盘腹蚁的亲缘关系更近。本研究分析认为，产生此种现象的原因可能是由于标本来源多样化导致的，即同一种蚂蚁，由于生境的不同导致了外部形态差异以及测量过程中可能存在视觉误差，致使个别性状测量结果具有一定误差，影响了数据的分析，但总体上与形态分类结果一致。

总体而言，形态特征测量值能够对昆虫外部形态的细微变异结构进行量化分析，可以反映物种在生态学和系统发育史上的差异，从而区分同源类群[25]。黄海燕[22-23]、张荣娇[24]、谷博[21]、Weiseri &Kaspari[25]、Csősz等[28]、Hazarika[26]和Samung[27]等都采用了形态测量学的方法开展了相关的研究，均证明该方法可用于蚂蚁物种分类。形态测量学方法对物种分类、区分相似种、研究物种间亲缘关系等方面均具有重要意义。但是同一种蚂蚁的形态特征是由内在基因和外部环境共同决定的，形态测量学不能对蚂蚁的外部特征进行完整描述和数据统计，不能单一的使用形态测量学进行分类学研究，需要同传统形态学方法相结合，才能进一步确定蚂蚁的分类地位。

4 结论

19 种盘腹蚁在14 个性状变量上存在差异，主要表现在胸长（MSL）、头宽（HW）、腹柄长宽比（LPI）和腹柄长高比 （DPI）这4 个性状上，这4 个性状基本涵盖该属19 种蚂蚁形态测量学研究中所涉及的14 个性状特征；主成分得分散点图能够明显区分该属19 种蚂蚁；通过系统聚类，将盘腹蚁属19 种蚂蚁分为4 支，第一支与第二支的相似度最高，亲缘关系最近，与第四支的相似度最低，亲缘关系最远；各支种间亲缘关系则最近，与其他支的种亲缘关系最远，其结果与主成分得分散点图的聚类情况以及形态特征分类结果基本一致。运用形态测量学方法对蚁科昆虫进行物种分类鉴定是可行的，具有重要应用前景，可为分类鉴定提供新的方法。