含二阶扰动补偿的交错并联变换器自抗扰控制

周雪松, 王博, 马幼捷, 陶珑, 杨清

(1.天津理工大学 天津市复杂系统控制理论及应用重点实验室,天津 300384; 2.天津大学 智能电网教育部重点实验室,天津 300072)

0 引 言

随着新型电力系统的发展,能源结构逐步向光伏微电网等新能源形式转变。但微网的多变量、强耦合等复杂特征也使得控制过程中存在着诸多问题。在此背景下,自抗扰控制(active disturbance rejection control,ADRC)技术因高鲁棒性、对模型的低依赖性以及针对非线性系统的快速收敛性质而在微网变换器控制领域得到广泛关注。依靠其核心机构——扩张状态观测器(extended state observer,ESO)对标称模型的外部扰动以及模型偏差部分的观测与跟踪,结合状态误差反馈控制率(states error feedback control law,SEFCL),可实现对微电网中双向变换器总和扰动的补偿,从而提高了控制系统的快速性与抗扰能力[1]。但由于高阶ADRC的稳定性证明及参数设计较为复杂,故传统策略通常只使用二阶以下的自抗扰控制器对微网变换器控制。

在光伏微电网中,介于直流母线与储能装置之间的双向直-直变换器(bi-directional DC-DC converter,BDC)的简化模型一般考虑为二阶形式[2]。但实际的BDC电路因寄生参数、外部噪声干扰以及开关过程的影响,其模型既不是线性的,微分方程也大于二阶。有研究表明,低阶ADRC对二阶以上的被控对象的控制效果会因动态响应速度缓慢而不能令人满意。其主要原因为,ADRC中低阶的ESO假定的被控对象也为低阶形式,而未被考虑的高阶部分、非线性成分与全部外部扰动一起被扩张为一阶状态变量。显然仅用一阶的输出去描述系统估计不准的部分(内扰)以及被控对象所受到的扰动(外扰)总和是不够全面和准确的。更严重的是,如果ESO环节对被控系统的估计模型与实际模型的阶数相去甚远或系统有较大幅度外部扰动时,这一不准确性会使得ESO的扩张维度(对总和扰动的估计量)的动态收敛速度更加缓慢,从而导致ADRC对总扰动的补偿过程产生延时。

针对这一问题,主要有预测补偿策略与延迟近似模型改进两类主流解决思路。在第一类思路下,文献[3]在自抗扰控制技术的基础上,结合史密斯预估补偿技术提出Smith Predictor-ADRC策略,使得瞬态响应和相位滞后得以改善,但其动态调节环节伴随着较大的能量波动。也有团队利用时滞补偿技术,通过各类智能预测算法来获得近似无延迟的输出反馈[4-5],但这类方法往往参数整定复杂。而对于第二类解决思路,其本质是在改造低阶ADRC使之匹配高阶对象[6]。文献[7]依靠非线性调整规则来应对延迟系统,从而在高阶控制的动态优化上取得了一定进展,但由于非线性稳定性域求解困难,因此不便于在实践中应用。而文献[8]从模型信息的角度研究,证明了当模型信息已知时改进ADRC动态时延更低的特性。但显然这一条件在工程上也很难满足。文献[9]针对二阶LADRC提出一种改进策略并用于高阶系统控制,改善了动态控制性能,且鲁棒性良好。综合来看第二种思路下的改进控制器因参数简单而更具实践意义。

本文针对BDC电路模型的自抗扰控制技术展开分析,重构了ESO和SEFCL环节。扩张出两维状态变量用于精确描述内扰与外扰的总和并对被控对象予以两阶补偿。通过对观测误差收敛过程的对比,指出传统ADRC控制器与被控对象阶数不匹配时跟踪性能与抗扰性能不佳的原因,阐述本文所提出的高阶扰动补偿型自抗扰控制器的解决机理,并给出参数整定方法。在仿真对比中,通过3种控制器对同参数BDC电路控制过程的对比,验证所提新结构的理论分析结论。最后总结提出的改进结构自抗扰控制器可在保持LADRC原有的控制结构稳定性以及简明的参数设计方法前提下,更好地满足被控对象面对较大扰动时,控制系统对跟踪性、抗扰性与鲁棒性的要求。

1 被控对象与传统自抗扰控制策略

1.1 交错并联式的双向DC-DC变换器模型

常见的光伏发电微电网结构如图1所示。其中,双向DC-DC变换器因拓扑结构简单以及较好的转换效率[10]而得到广泛应用。

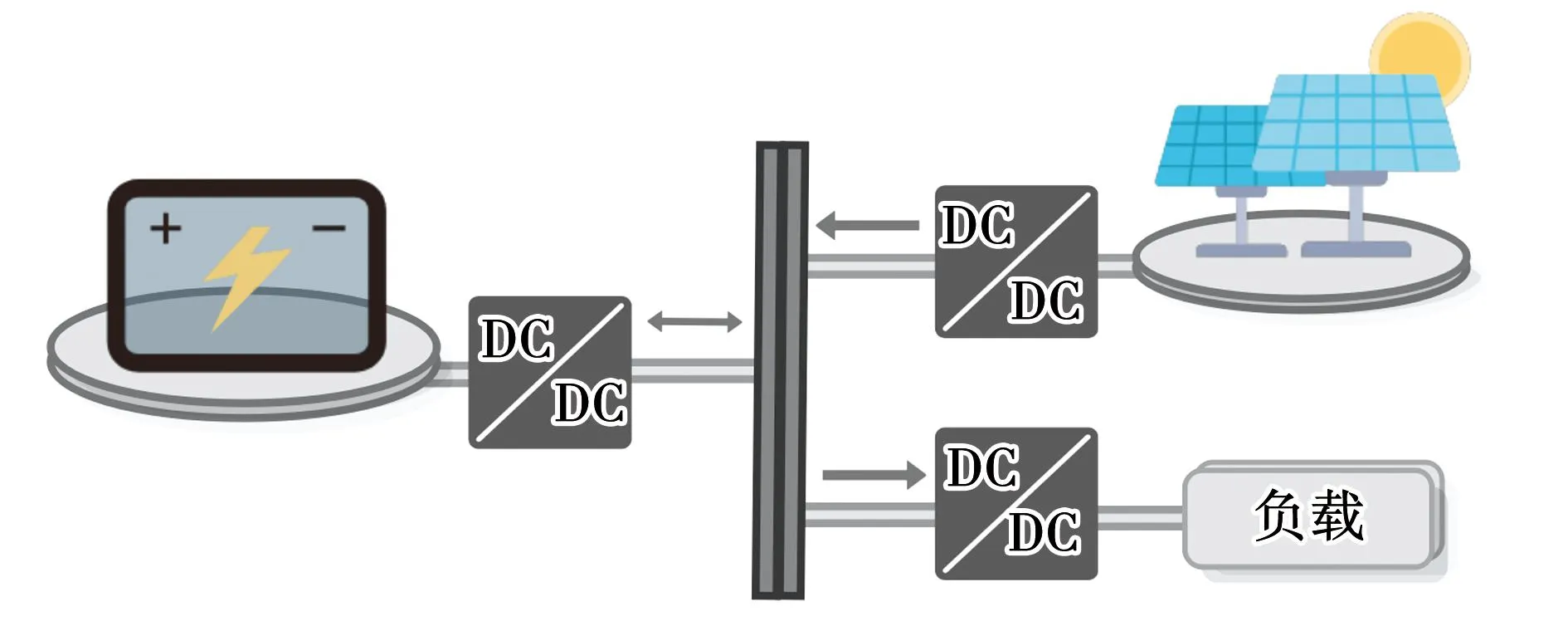
图1 光伏储能系统Fig.1 Photovoltaic energy storage system

为了对输出电压纹波加以抑制并提高输出电流与总功率,常采用偶数相的BDC电流交错并联构成所需的电力电子变换器件。图2为本文所研究的六相交错并联形式的双向Buck/Boost电路的拓扑结构。

将6个结构和参数完全相同的双向Buck/Boost变换器交错并联,每一相导通信号依次移相60°。使得在一个导通周期T内,各相的控制间隙为T/6,且周期内各相的导通时间相等,考虑开关频率为100 kHz,则相间间隔约为1.667 μs。由文献[11]可知,每一相的电路模型可用状态空间平均法得到小信号模型。

以占空比为输入,电容电压为输出的等效传递函数为

(1)

以占空比为输入,电感电流为输出的等效传递函数为

(2)

式中:Vin与d表示变换器输入电压和动态占空比;uc与iL1分别为电容电压和电感电流;R、L、C为各相BDC电路的阻抗参数。由式(1)、式(2)可推得iL到uc的过渡传递函数为

(3)

依据上述传递函数,可以将被控对象转化为标准的双闭环控制框图如图3所示。

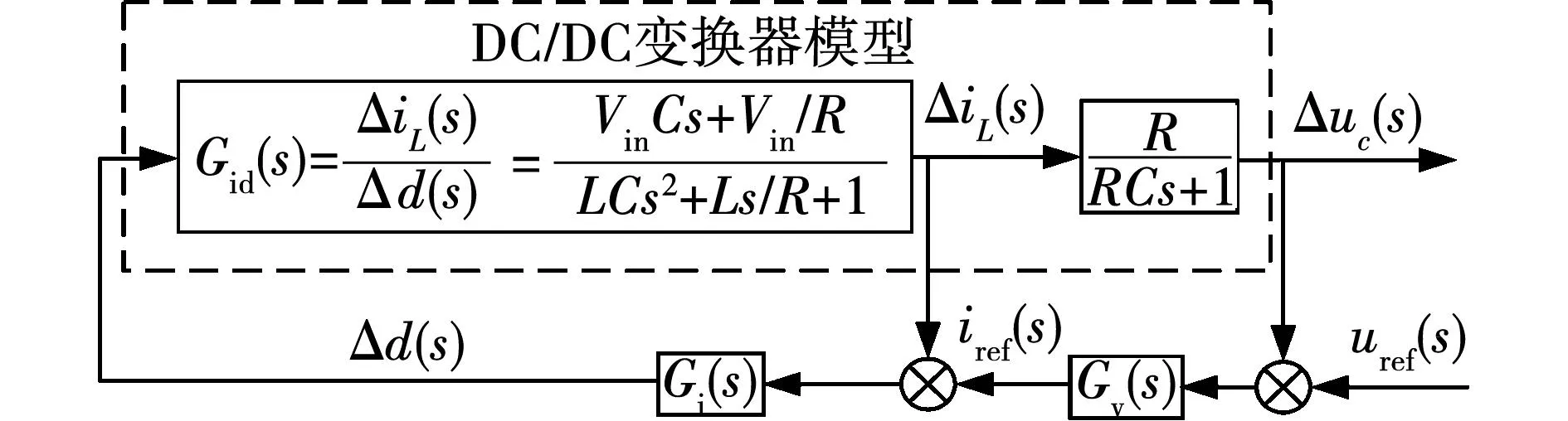
图3 被控模型的双闭环控制结构Fig.3 Double closed-loop control structure

1.2 传统三阶自抗扰控制策略

一般的模型估计不准且含扰的高阶系统考虑为如下形式:

y(n)(t)=g(y(t),y(1)(t),y(2)(t),…,y(n-1)(t),n(t))+bu(t)。

(4)

其中u(t)、y(t)、n(t)分别为系统控制量、输出量及被控对象受到的外部干扰。由上述方程可见,综合函数g(·)表征了被控系统模型状态变量间的耦合关系,其既可以是非线性的,也可以是时变的。而b是无法准确获取到的被控系统控制量增益,通常只能使用参数b0估计。

传统的三阶自抗扰控制策略将此不确定的高阶系统估计为确定的两级结构,而将高于二阶的成分视为总和扰动的一部分,从而全部非理想的成分可定义为总和扰动函数为

f(t)=g(y(t),y′(t),y″(t),y(3)(t),…,y(n-1)(t),n(t))+(b-b0)u(t)+y″(t)。

(5)

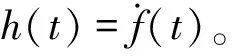
y″(t)=f(t)+b0u(t)。

(6)

传统三阶自抗扰控制策略分别将简化二阶系统的输出量y(t)及其导函数y′(t)记为状态变量x1与x2,而将总和扰动f(t)视为原系统的扩张状态变量x3,则式(6)的原二阶系统可扩张为三阶状态方程形式:

(7)

针对此扩张系统可设计传统LESO如下:

L(z1(t)-y(t))。

(8)

式中观测器增益矩阵为

上式描述的传统三阶扩张状态观测器结构如图4所示。依靠LESO的收敛特征,可将系统状态变量的估计值z1和z2导出,并对总和扰动z3的变化情况实时跟踪[13-14]。依靠SEFCL环节对总扰动主动补偿作用,可使整个控制系统由被动抗扰的形式转换为主动校正的模式。

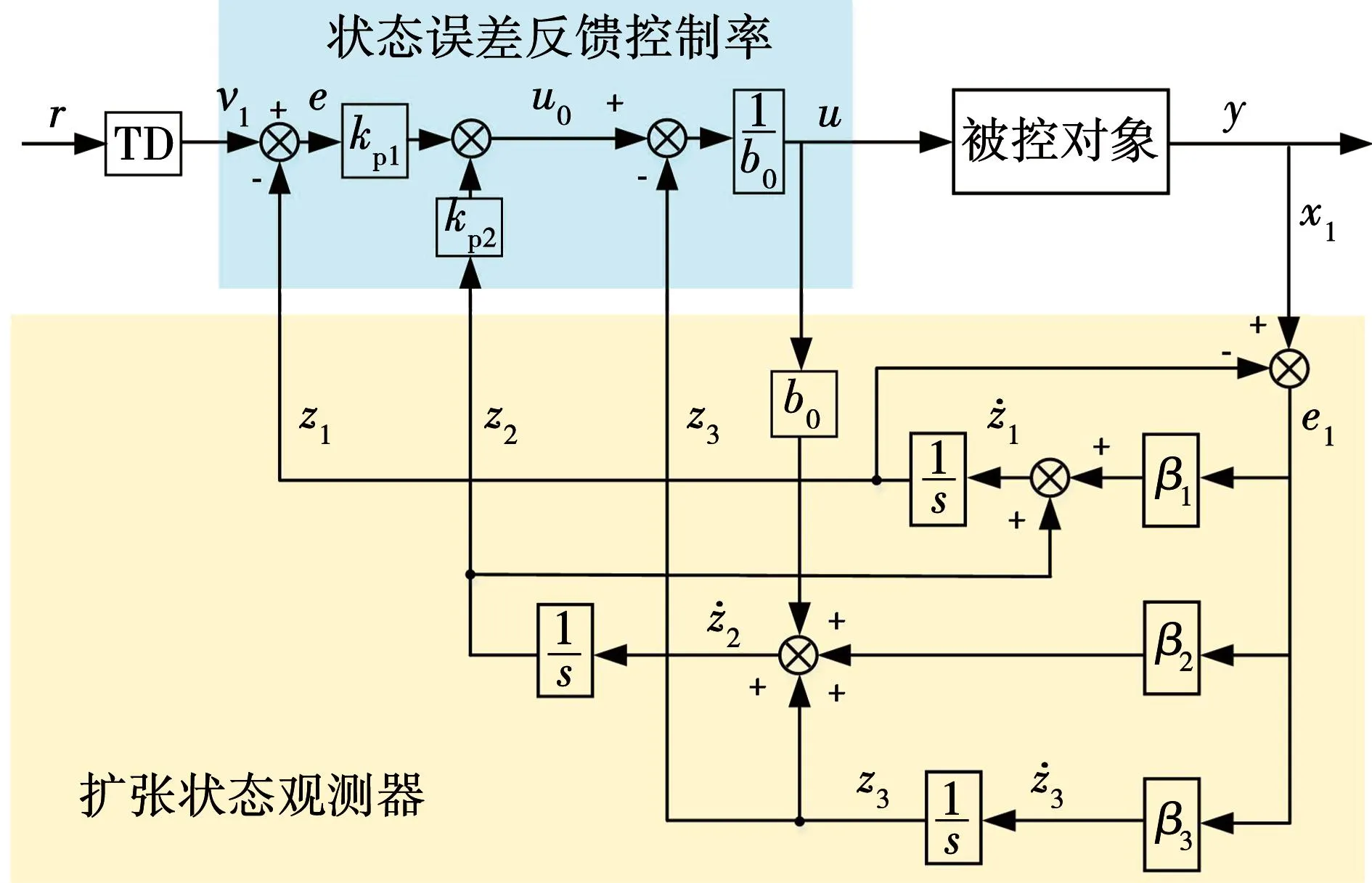
图4 传统ADRC控制器基本结构Fig.4 Basic structure of traditional ADRC

系统状态误差的线性反馈率可设计如下[15]:

(9)

式中:参数kp1与kp2均为控制器增益;u0为中间控制量,则最终的控制率为

(10)

由式(6)、式(9)、式(10)结合图4可知,模型估计不准且含扰的高阶被控对象在t→∞时,满足

y″(t)=f(t)+u0(t)-z3(t)=u0(t)。

(11)

由上式可见理想的增益矩阵参数下,仅靠扩张维度便可补偿被控系统的总和扰动,使得原有的高阶被控对象模型简化为二阶形式。若将上述ESO与误差反馈控制率环节组合可得到基本的LADRC控制器结构。但考虑到起始阶段系统输出状态同参考信号间存在较大的偏差,直接使用误差信号构建控制率会带来较大的高频颤振同时伴随动态偏差过大的问题[16-17],因此通常引入跟踪微分环节(tracking differentiator,TD)加以改善。可知针对二阶被控系统设计的基于离散最速综合函数的非线性TD环节结构如下:

(12)

跟踪微分器可将给定的输入信号r(t)柔化为启动信号v1(t)。有文献[18]知TD环节可在保证稳定性基础上,缓解启动震荡并提高动态响应速度。传统三阶LADRC控制器的完整结构图4所示。

2 二阶扰动补偿型自抗扰控制策略

2.1 二阶扰动补偿型扩张状态观测器

由文献[19]知,光伏微电网的多变量、高纬度、干扰模型复杂等特征正是影响低阶ESO动态响应速度的主要因素。针对这一问题,可引入扰动模型的高阶信息,设计如下形式的改进结构ESO:

(13)

式(13)所描述的改进形式的扩张状态观测器在保持用两阶状态变量描述被控对象模型的基础上,额外生成2个自由扩张维度的变量对系统收到的外部扰动及理想模型描述不准的成分进行跟踪与补偿。因此改进后的控制器拥有2个维度的扰动描述变量,简称为二阶扰动补偿型自抗扰控制器(ADRC with two dimensional state variables representing disturbances,ADRC-TSRD),其核心机构称为ESO-TSRD。通过配置增益矩阵L可实现ESO-TSRD对系统状态变量和总扰动的实时跟踪。最终期望状态变量z1和z2对被控对象的输出与其微分的准确跟踪,状态变量z3和z4对总和扰动的同阶及高阶分量的准确跟踪。

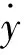
(14)

式中kp与kd为控制器增益,通过引入参考微分误差e2(t)的前馈结构可有效加速状态误差反馈控制率中e1(t)→0过程,从而实现对动态响应速度的改进,后续仿真对比可对此点说明。将上述各部分组合可得改进后的二阶扰动补偿型ADRC-TSRD的结构如图5所示。

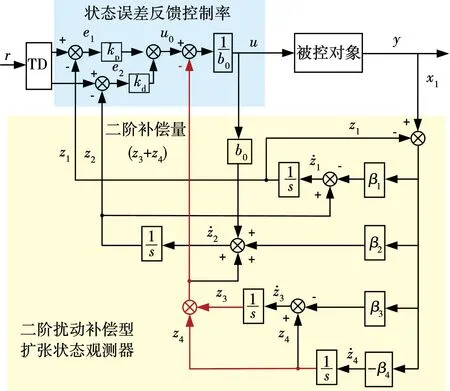
图5 ADRC-TSRD结构Fig.5 Structure of ADRC-TSRD

2.2 参数整定方法

式(13)中,矩阵形式的ESO-TSRD微分方程组可导出输入控制量u(s)和被控对象输出量y(s)与ESO的各阶状态变量间的关系为:

(15)

利用带宽法对ADRC-TSRD的ESO环节的参数整定[20],配置观测器极点于ωo处可得到等值关系为

(s+ωo)4=s4+β1s3+β2s2+(β3+β4)s+β4。

(16)

因此有对应参数匹配规则为:

(17)

由式(9)～式(11)可知,控制器跟踪值接近收敛时有

y(n)(t)=f(t)+u0(t)-zn+1(t)≈u0(t)。

(18)

结合式(14)可得ADRC-TSRD控制下的二阶系统满足

(19)

因此有控制系统传递函数为

(20)

将系统极点配置与ωc处,于是有参数设计如下:

(21)

式中ξ和ωc分别为控制系统阻尼比与控制器带宽。由文献[21]知,取ξ=1时可得到较好的动态性能,故整个控制器的参数可简化为对观测器带宽ωo和控制器带宽ωc的选择。

2.3 ADRC-TSRD稳定性分析

由式(14)可知,控制器的输出满足

(22)

代入式(15)～式(21),考虑微分跟踪结果理想时,有闭环控制系统满足

(23)

其中:

Gc(s)=

(24)

12ωos3+6ωcωos2+4ωcs3]。

(25)

由式(23)～式(25)可得图6所示ADRC-TSRD控制系统的等效模型。

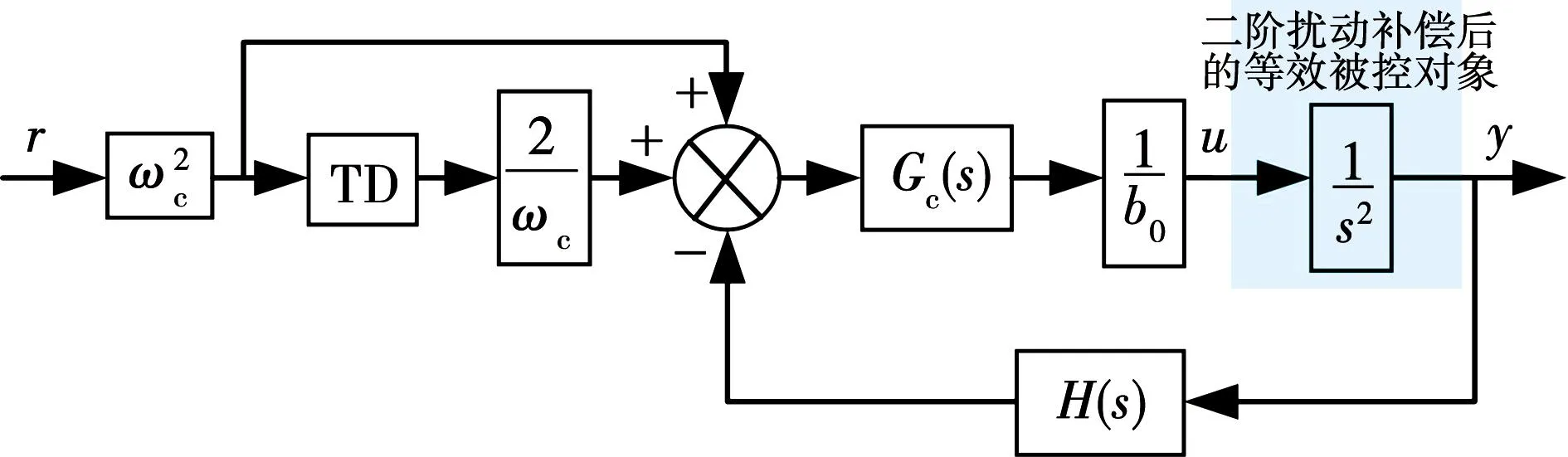
图6 ADRC-TSRD控制系统等效模型Fig.6 Equivalent model of ADRC-TSRD control system

由梅森公式,可将ADRC-TSRD控制系统的等效模型简化为闭环传递函数为

G(s)=

(26)

其中:

若期望控制系统稳定,须保证不等式组[22]成立,即:

(27)

利用不等关系可简化上式,并得到解如下:

(28)

3 ADRC-TSRD控制器系统分析

3.1 ESO-TSRD对扰动的观测过程分析

由式(4)～式(7)可知,二阶被控对象的模型的实际总和扰动满足:

(29)

(30)

由式(31)、式(32)可构造实际扰动到被控对象的扰动估计值间传递函数为

(31)

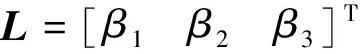
(32)

又由式(29)可知,总和扰动实际值满足关系f(s)=-b0u(s)+s2y,故被控对象的实际扰动到ESO-TSRD估计扰动同阶分量之间的传递函数为

(33)

由式(15)知总和扰动的高阶估计分量为

(34)

故被控对象的实际扰动到改进ESO所估计扰动的高阶分量之间的传递函数为

(35)

对比式(33)、式(35)、式(37)可见,通过增加线性化模型描述总和扰动的一个自由度,ESO-TSRD的同阶扰动估计传递函数G11(s)增加了一个自由极点和零点,而高阶分量传函G12(s)则增添了一个自由极点与固定虚轴位置的零点。

由式(33)、式(35)可导出总和扰动的估计传递函数为

(36)

通过式(33)～式(36)中传递函数与传统ESO结构的对比可见,合理配置的新增极点的位置可减小相位变化范围从而提高工作频段的快速性。设计同阶分量传递函数的自由零点位置可校正观测器根轨迹从而提升ESO-TSRD的收敛性能,而固定与虚轴位置的高阶分量传递函数的零点可带来更大的带宽从而加速观测器高阶分量的收敛速度,但大带宽也会造成噪声的放大作用,有传统ESO与改进结构的复频域图像对比如图7所示。

图7 改进前后的ESO环节幅相曲线比较Fig.7 Comparison of amplitude and phase curves of ESO

由对比可见,改进后系统的相角裕量因工作频段的20 dB/dec转折而增加,从而改善了稳定性。但同时这一转折也会对高频段噪声带来放大效应。若考虑将极点独立配置在高频扰动附近,则可以通过降低噪声频段增益的形式进一步提升抗扰能力。如图8所示,在保障观测器带宽均值不变的条件下,对称的调整各极点位置。由幅频曲线可知,随着极点逐步靠近高频段,噪声增益显著减小,但相频曲线中的相角裕值也相应变差。可见,利用带宽法配置参数更注重于对稳定性的考量,而观测器带宽均值不变原则下逐步改变极点分布,使个别极点靠近噪声所在的高频段,可带来更好的抗扰的能力。因此在ESO-TSRD补偿总扰动时,可根据实际系统的需要在带宽法基础上进一步配置观测器参数。

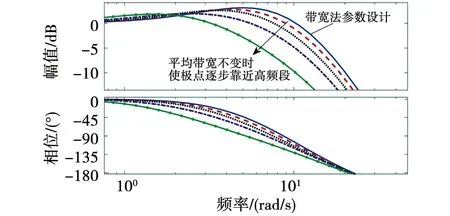
图8 极点向高频段移动时系统稳定性和抗扰性的变化Fig.8 Changes of system stability and immunity when poles move to high frequency band

3.2 ESO-TSRD对噪声抑制性能分析

在实际系统中,除了外部干扰外,还存在着输入、输出侧的测量噪声。考虑线性系统的齐次叠加性质,由式(15)可知,被控对象的输入测量噪声Nr(s)以及输出测量噪声Nc(s)对ESO输出的影响为

(37)

故改进ESO的输出侧等效噪声传递函数为

(38)

改进ESO的输入侧等效噪声估计传递函数为

(39)

采用式(19)中ADRC-TSRD参数整定方法设计改进ESO的增益矩阵,并代入式(38)、式(39)可得:

(40)

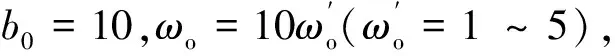
图9 不同带宽下变换器端口噪声的频域特性曲线Fig.9 Frequency domain characteristic curves of converter port noise under different bandwidths

3.3 ADRC-TSRD的抗扰性数值分析

由改进型ADRC-TSRD简化模型结合式(28)可知,广义扰动和模型不精确导致的内部扰动的总和到被控对象输出之间的传递函数Gf(s),以及参考信号到对象输出间的闭环传递函数G(s)分别为:

(41)

代入式(24)、式(25)中,H(s)和Gc(s)的表达式可得考虑扰动作用下的控制系统等效传递函数为

(42)

其对应的ADRC-TSRD控制系统含扰模型如图10所示。

图10 含扰的ADRC-TSRD控制系统等效模型Fig.10 Equivalent model of ADRC-TSRD control system with disturbance

考虑外部扰动f(t)取不同幂次时,由式(42)可分别算得传统LADRC和改进后的ADRC-TSRD控制下闭环系统的响应函数,如表1所示。

表1 自抗扰控制器在各幂次扰动下响应函数对比

(43)

由表1结合式(43)可知,初始误差函数f(t)依次取阶跃函数、斜坡函数时,改进型ADRC-TSRD控制器可在过渡过程结束时完全跟踪误差的变化量,而传统LADRC控制器会在斜坡误差函数的作用下产生一个恒定的稳态误差E1无法收敛至0。在加速度误差函数作用下,两种ADRC控制模式对扰动的跟踪均出现了一定的误差量,不同的是使用2个扩张维度共同描述总扰动的ADRC-TSRD控制器可通过升高控制器带宽ωc和观测器带宽ωo以改善静态误差E4。而传统ADRC控制下的系统会因扰动补偿的阶数过低而逐渐失去跟踪能力,导致跟踪误差E2t+E3不断扩大。以上对比说明采用二阶扰动补偿的ADRC控制器具备更强的抗扰能力。

4 仿真实验及对比分析

分别使用双闭环PI、LADRC与改进后的ADRC-TSRD对表2所示的双向DC-DC电路进行控制。其中ADRC-TSRD据2.2节的参数设计方法整定,与之对比的LADRC和双闭环PI控制器参数分别采用带宽法和环路法设计。

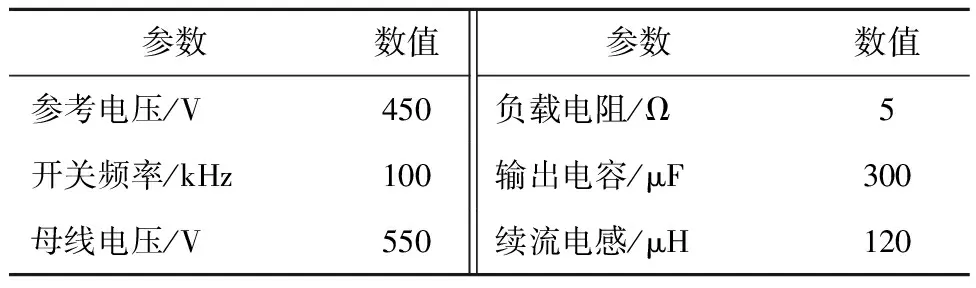
表2 仿真参数Table 2 Simulation parameters

在保证带宽固定的基础上,Double-loop PI参数由环路法设计,而自抗扰参数分别设计为ADRC-TSRD:{β1=40,β2=600,β3=600,β4=10 000},LADRC:{β1=30,β2=300,β3=1 000}。将其应用至电压跟踪调整、母线扰动抑制、负载扰动抑制3类常见工况的数字仿真平台,并分别对改进ADRC的跟踪性能、抗扰性能、鲁棒性能进行模拟校验。

4.1 动态跟踪性能对比

图11为ADRC-TSRD跟踪性能对比图。

图11 ADRC-TSRD跟踪性能的对比Fig.11 Comparison of tracking performance

可将图11(a)、(b)中跟踪波形描述为表3,其中a为控制过程中的最大动态偏差比,计算为正时表征超调量,为负时代表动态降落。IAE为绝对误差积分指标。由表3可以看出在本文给定的参数整定方法下,改进后的二阶扰动补偿型ADRC与双闭环PI控制器均很好的实现了对交错并联式DC-DC变换器的纹波控制。采用双闭环PI的被控对象与采用传统LADRC的被控对象相比,对电压调整信号的跟踪情况有相似的表现。但在初始偏差较大的启动环节,因LADRC仅有的一阶扩张变量对总和扰动的跟踪速度较慢,使得其最大动态偏差比起双闭环控制策略有一定的突出。而改进后的ADRC-TSRD控制策略因采用了两阶状态变量共同描述总和扰动,使得改进结构对目标信号的跟踪能力显著增强。

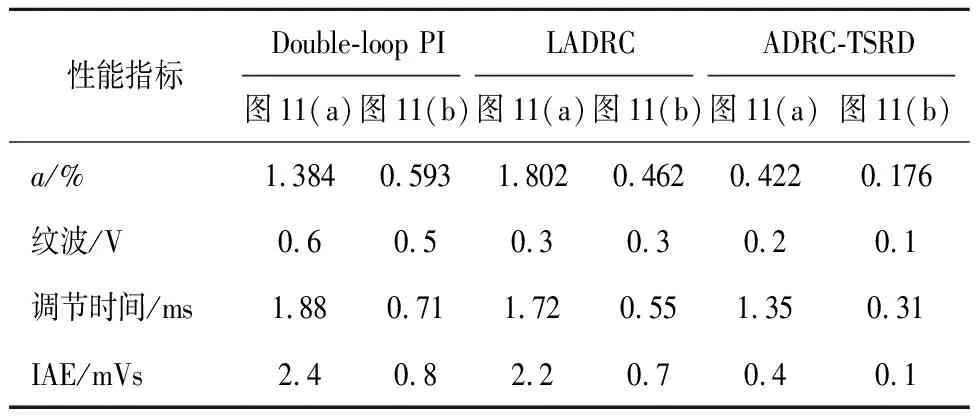
表3 跟踪效果对比Table 3 Tracking performance

4.2 抗扰性能对比

图12为ADRC-TSRD对母线侧扰动的抑制效果图。表4为电源侧抗扰效果对比。

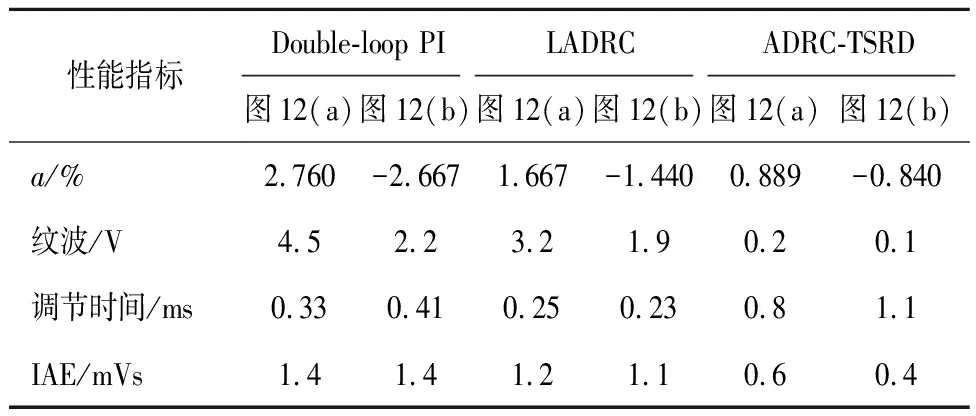
表4 电源侧抗扰效果对比Table 4 Anti-disturbance effects on power side

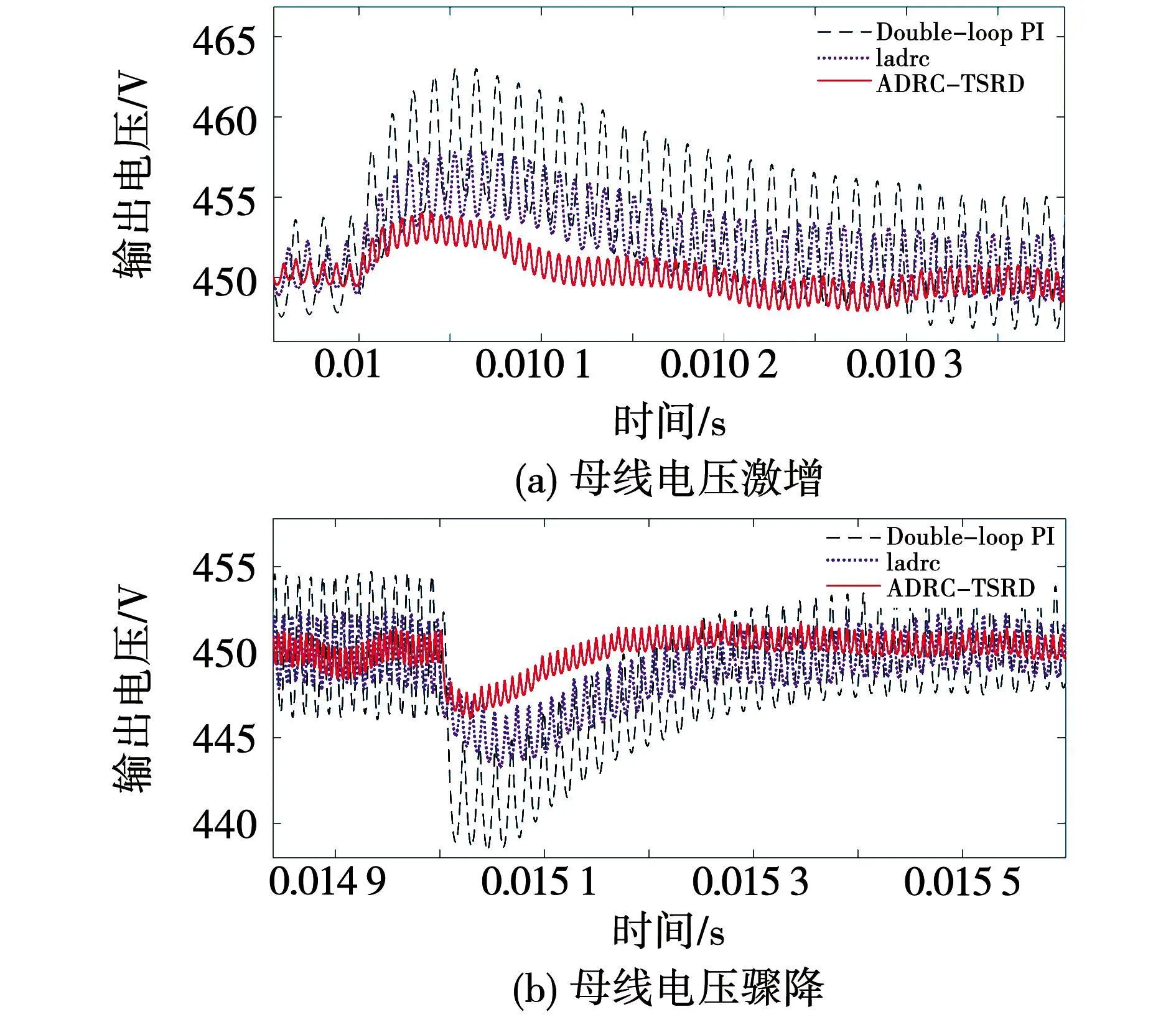
图12 ADRC-TSRD对母线侧扰动的抑制效果Fig.12 Anti-disturbance effects on power side

从图12中不难看出引入母线侧扰动后的稳压曲线比起跟踪过程具有更大的纹波和动态偏差值。对比表4中传统LADRC与二阶扰动补偿形式的ADRC的抗扰效果可知,低阶自抗扰控制器在应对含扰动对象时,改进后的高阶补偿结构对输入测噪声或扰动有良好的抑制效果,这与前文中对ESO-TSRD噪声抑制过程分析的理论结果一致。从IAE指标和调节时间来看,因线性自抗扰控制器所拥有的主动抗扰能力,其所控制的稳压曲线比双闭环PI控制策略有更好的动态恢复能力,通过快速抑制母线侧的能量波动可使其更符合预期的闭环动态响应要求。而改进后的ADRC-TSRD控制器更是在主动抑制扰动的基础上,通过扩张维度加速了收敛过程。从调节时间上看,面对母线侧电压激变扰动的模拟工况时,ADRC-TSRD的恢复时间相较传统LADRC缩短了约37%,动态偏差范围缩减了约42%。

图13为ADRC-TSRD对负载侧扰动的抑制效果图。表5为负载侧抗扰效果对比。

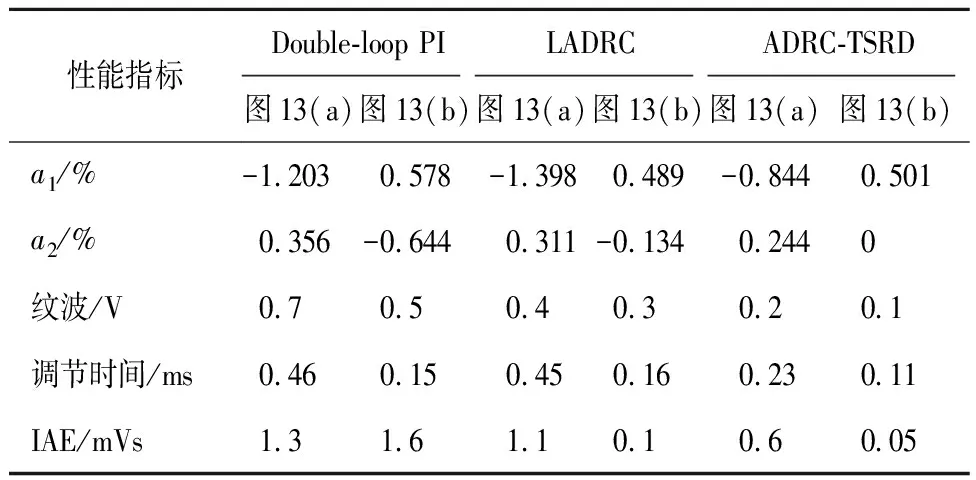
表5 负载侧抗扰效果对比Table 5 Anti-disturbance effects on load side

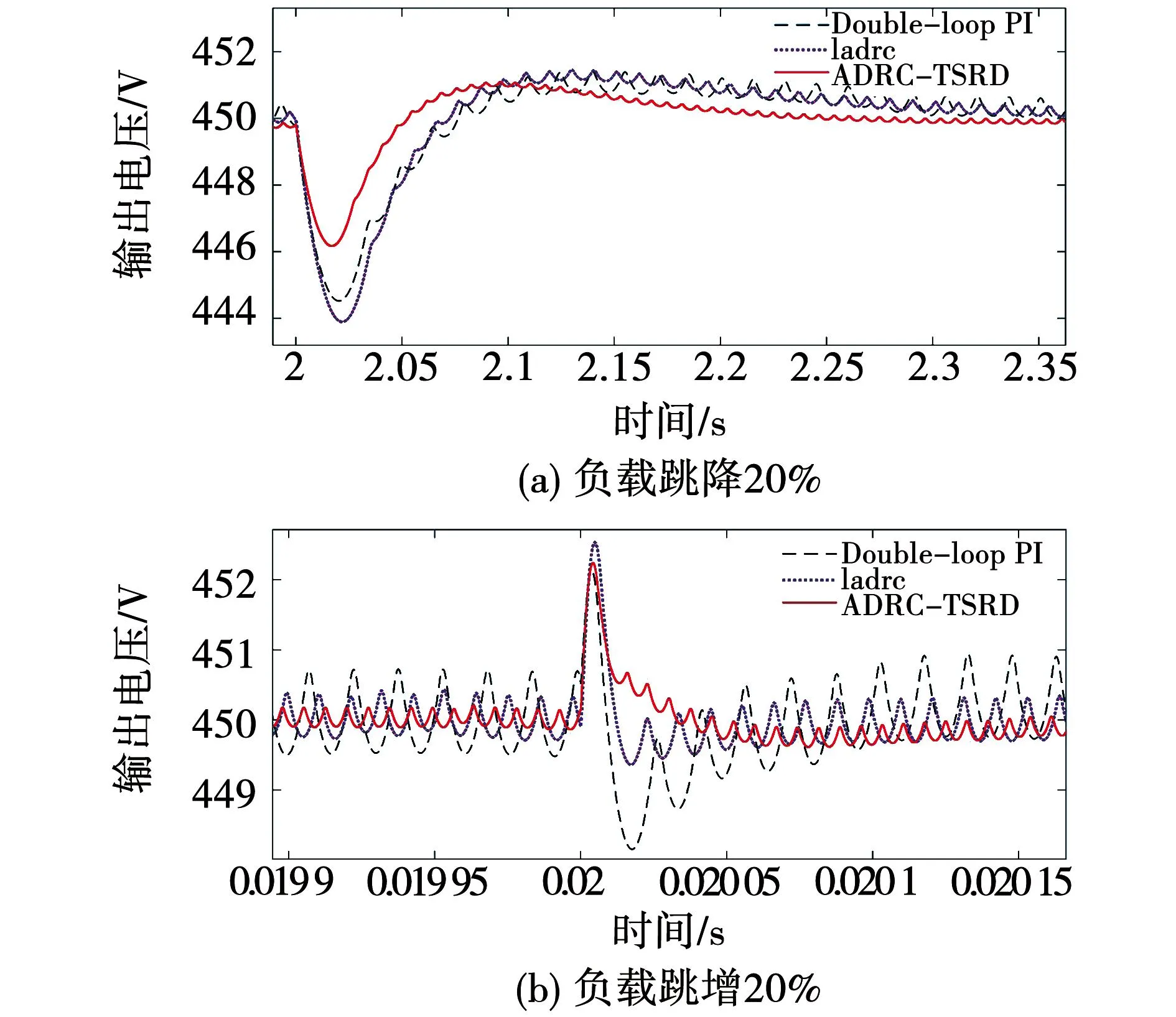
图13 ADRC-TSRD对负载侧扰动的抑制效果Fig.13 Anti-disturbance effects on load side

表5中,a1和a2分别指扰动抑制动态过程的一次波动和二次波动的最大偏差比。在减负荷20%的工况下,3种不同控制策略引起的二次波动偏差值和恢复时间未有明显的区别,但二阶扰动补偿型ADRC依靠其对总扰动快速跟踪补偿的特质使得动态过程的一次偏差值显著减少。而在增负荷20%的模拟工况下,由于自抗扰控制器的无超调控制策略,LADRC与改进后的ADRC-TSRD均未有明显的二次动态降落,而双闭环PI控制由于采用了较为激进的控制参数,因此具有更好的快速性,但也带来了一定的高频振荡和动态降落增幅。总体上看,补偿型ADRC在高比率负荷投切与母线电压激变两类场景下,其对动态扰动的抑制响应结果均表现出了恢复时间短、超调量小的特点,稳压控制效果明显优于双闭环PI控制器和传统LADRC控制器。

4.3 鲁棒性校验

保持控制器参数不变,负载电阻、母线电压等外部状态也不发生偏移的情况下,设被控过程的系统变换器内部电容以及电感参数在标称值±15%的范围内随机变化,且服从均匀分布。对3类控制器各进行25次重复实验,统计各控制器的跟踪过程绝对误差积分(integral absolute error,IAE)指标和抗扰过程IAE指标。这里的过程IAE指标定义为绝对误差积分值除以参数的本次随机生成值[24]。为验证前文所述的观测器带宽对系统的影响,设置ωo=K1ωc,其中K1分别取100、101、102、103,有横轴为跟踪IAE纵轴为抗扰IAE的性能分布如图14所示。其中性能指标分布点越接近原点意味着越好的跟踪性能和抗干扰恢复能力,而越密集的分布意味着更好的闭环系统鲁棒性能。

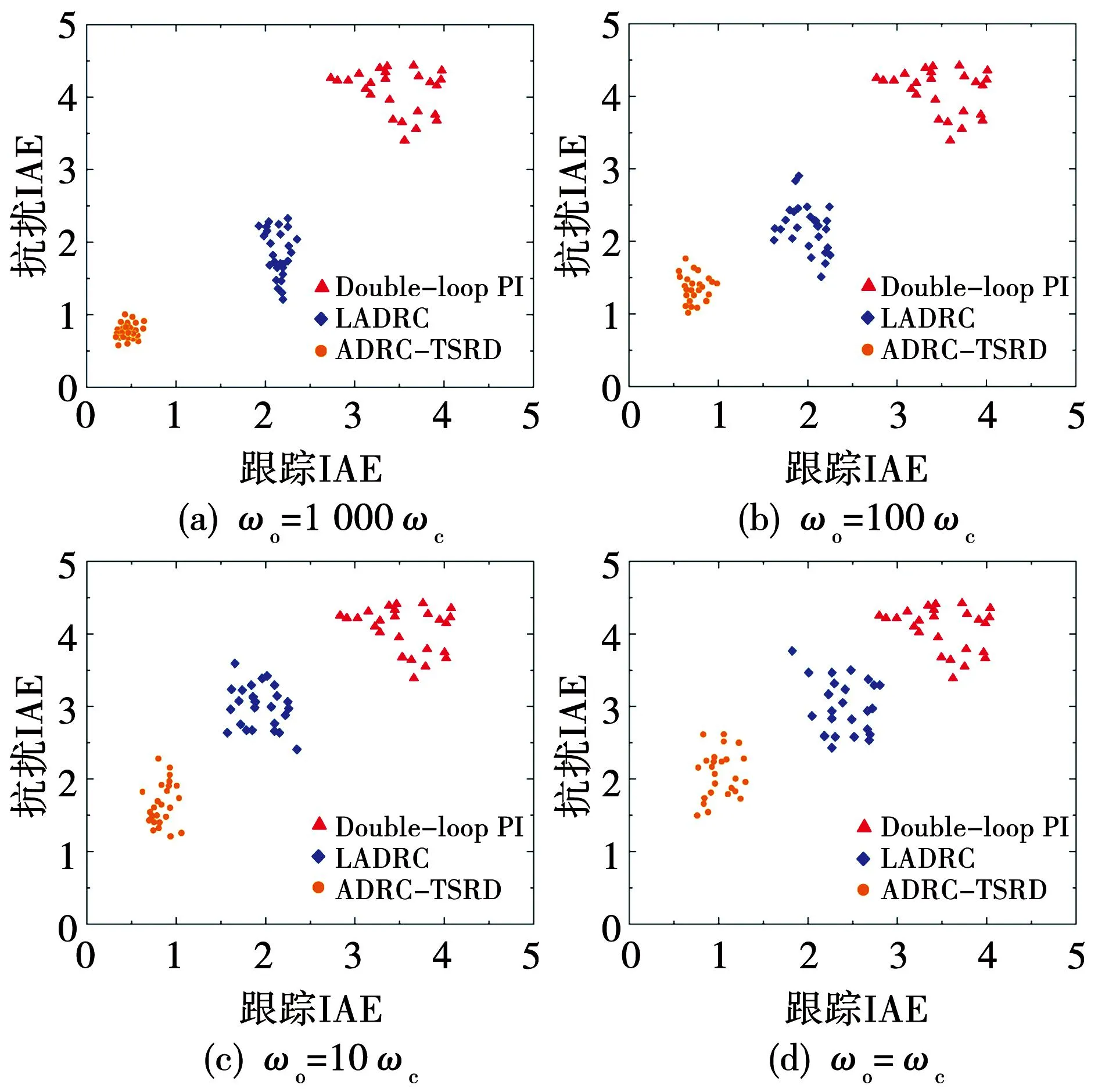
图14 鲁棒性对比Fig.14 Robustness comparison

由图14可知,在内部参数偏移标称值的情况下,不同内部参数的双向DC-DC变换器在自抗扰控制器作用下均可在较小数量级的恢复过程后实现对目标信号的稳定跟踪。在不同带宽下,参数偏移时二阶扰动补偿型ADRC可以保持较好的控制效果,而同一带宽下改进型ADRC鲁棒性显著优于LADRC和双闭环PI控制器,主要表现为二阶补偿型ADRC的面积式IAE性能指标相比于ADRC和PI控制器分布更为集中。对比4组不同ωo的结果可看出,带宽的大小会影响ADRC控制器的鲁棒性,且对二阶扰动补偿型ADRC的影响更为显著。此外,在K1=104及更高幂次的情形下进行鲁棒性校验时,ADRC会出现大幅度抖震而失稳的情况,因此未在图中给出。因此当扰动频率低时,应当选取小带宽。过大的带宽,会使得扰动量、自然输出抖震变大,可能造成自抗扰控制器失去稳定。但是随着扰动频率增加,大带宽对扰动的估计补偿作用明显更强,即扰动的补偿量会变大。当扰动频率增加时,用大一点的带宽可以更好地抑制扰动。在保证稳定性的前提下,ωo越大时ADRC-TSRD的鲁棒性能越佳。

5 结 论

光伏微电网中的BDC变换器在未来分布式能源的发展过程中占据越发重要的地位。然而微电网运行过程中变换器端口存在着负荷突变、母线功率波动以及变换器内部的建模误差等问题时刻在影响着微电网运行的稳定性。据此,本文提出一种ADRC-TSRD控制策略,以改善光伏微电网的动态性能。改进的控制策略通过重构ESO中对总扰动的描述形式实现了提高扰动观测精度与动态速度的目的,从而及时将变换器补偿为串联积分模型。此外,在反馈律中还引入了参考信号的跟踪微分补偿环节,通过跟踪性能的对比揭示了改进结构对输入信号跟踪精度的影响。从性能分析和实验结果可看出,与传统自抗扰控制器和双闭环PI器相比,基于ADRC-TSRD的微电网系统在多种运行条件下均具有更好的信号跟踪能力、抗干扰能力与鲁棒性能。更重要的是,经过参数简化后的ADRC-TSRD在控制器阶数升高的同时具备同传统LADRC相同的参数整定便捷性,显然,与LADRC双闭环PI控制策略相比,ADRC-TSRD更适合于多变量、强耦合、含严重未知扰动和系统参数不准确性的光伏微电网运行场景,因而具备较好的工程运用潜力,望本文能为各类储能微电网的应用提供更多思路。