双三相永磁同步电机驱动系统简易容错控制方法研究

石鹏川, 王学庆, 贺明智, 毛耀, 王政

(1.四川大学 电气工程学院,四川 成都 610065; 2.中国科学院 光电技术研究所,四川 成都 610209; 3.中国科学院 光束控制重点实验室,四川 成都 610209; 4.东南大学 电气工程学院,江苏 南京 210096)

0 引 言

近年来,多相电机驱动在工业界中得到越来越广泛的关注,尤其适合大功率高可靠性的应用场合,例如电梯、航空航天、电动汽车和舰船推进等应用领域[1-4]。和传统的三相电机比较,多相电机具有低转矩脉动、大功率、高可靠性和容错能力强等优点[5-7]。由于双三相电机通过两套三相绕组可以消除六次转矩脉动[8],在众多多相电机中优势明显。

与三相电机相比,多相电机具有更多的冗余相数,因而具有更强的容错能力。通常可转换电力电子变换器的短路故障为开路故障,因而电机驱动中的开路故障研究甚为广泛[9]。传统意义上,为获得等效旋转磁动势,对于电机驱动的缺相故障需要更改调制方案、容错参考电流和整体的控制框架等。文献[10]把缺相故障的六相电机重构成五相电机,基于新的五相电机模型和新的空间矢量图实现电机的容错控制。文献[11]将五相电机缺相故障下新构建电压空间矢量用作模型预测控制的候选矢量并配合容错电流参考值来实现缺相故障容错控制。在多相电机驱动开关管的开路故障容错控制方面,该类故障通常直接看作缺相故障进行容错[12]。然而,该方案无法充分利用故障桥臂相的剩余健康开关管,因而没充分利用多相电机驱动系统的容错性能。

传统的电机容错控制方法为电机的容错控制奠定了基础,提供了许多切实可行的解决方案,然而依然存在一些问题有待解决。例如,多相电机的传统容错控制策略通常需要改变电机模型、调制策略和控制框架,使容错控制复杂度增加,进一步增加容错控制的计算量,降低了直流侧直流电压的利用率,同时在电机容错过渡过程中易造成系统的不稳定。为了解决传统多相电机驱动系统容错控制方法存在的问题,本文针对多相电机驱动系统开路故障提出基于虚拟健全系统思路的简易容错控制方法,简化系统设计,降低容错控制复杂度。提出的容错控制方法同样适用于其他相数的多相电机驱动系统。

1 双三相电机数学模型

1.1 六相静止坐标系数学模型

图1所示为两电平双三相永磁同步电机驱动系统结构图,两套三相绕组空间互差30°,中性点相互隔离。

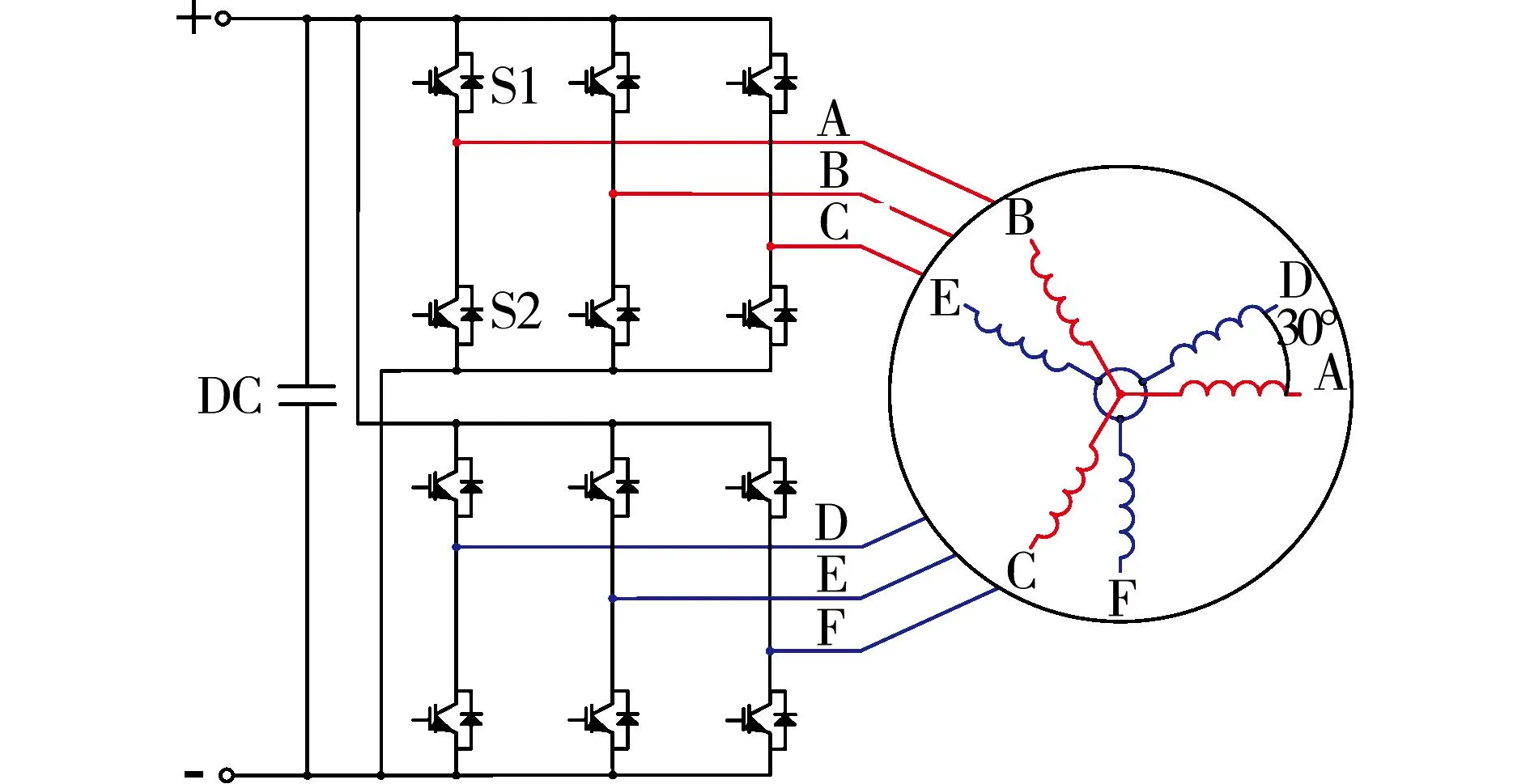
图1 两电平双三相永磁同步电机驱动系统结构图Fig.1 Configuration of two-level inverter-fed dual three-phase PMSM drive

忽略磁饱和,漏电感和铁耗影响,并将电机绕组看作正弦均匀分布,以简化双三相永磁同步电机的数学模型。双三相永磁同步电机六相静止坐标系下的电压方程和磁链方程可表示如下:

(1)

其中:us为定子电压矢量;is为定子电流矢量;ψs为定子磁通矢量;Ls为定子电感矢量;ψf为永磁铁(转子)磁通峰值;θe为转子的电角度。位置函数为:

(2)

1.2 矢量空间解耦矩阵

双三相永磁同步电机是一个高阶非线性强耦合系统,上述特征使分析和控制变得较为复杂。通过运用空间矢量解耦(vector space decomposition,VSD)方法[13],双三相永磁同步电机的数学模型可解耦为3个两两正交的坐标系:α-β,x-y,o1-o2。α-β平面下的分量参与电机的机电能量转换,因此α-β平面也称作转矩平面;x-y平面下的分量不参与机电能量转换,但产生额外谐波损耗,因此x-y平面称为谐波平面;o1-o2平面对应零序分量。双三相永磁同步电机空间矢量解耦矩阵如下:

(3)

1.3 同步旋转坐标系数学模型

中性点隔离的双三相永磁同步电机中ABC三相线性相关(iA+iC+iB=0),DEF三相线性相关(iD+iE+iF=0),故驱动系统的电流控制维度是四维。从空间矢量解耦矩阵角度理解,中性点隔离的双三相永磁同步电机不存在零序分量,剩余α-β-x-y四维控制变量。通过将双三相电机模型α-β坐标系转换到d-q同步旋转坐标系,可进一步简化双三相电机数学模型。双三相电机同步旋转变换矩阵为

(4)

联立式(1)～式(4),可以得到中性点隔离的双三相永磁同步电机旋转坐标系下解耦的电压方程和磁链方程:

(5)

(6)

式中:Ld和Lq分别为d轴和q轴电感;Lls为定子漏电感。

双三相电机电磁转矩方程可表示为

Te=3np(ψfiq+(Ld-Lq)idiq)。

(7)

2 简易容错控制

2.1 虚拟健全系统

传统双三相电机缺相故障容错控制方法通常将故障电机看作非常规的五相电机,如图2(a)所示。因此,该类方法通常需要构造新电机的数学模型、解耦控制和空间矢量图。本文提出的虚拟健全双三相电机,将缺相故障下的双三相电机看作一个虚拟健全的双三相电机,如图2(b)所示。新增的约束条件为故障相的参考电流为零。双三相电机采用虚拟健全容错思路,无须改变故障电机的数学模型、控制框架和调制策略,大幅简化了容错控制系统的设计,为双三相电机容错控制提供了一种新的思路。

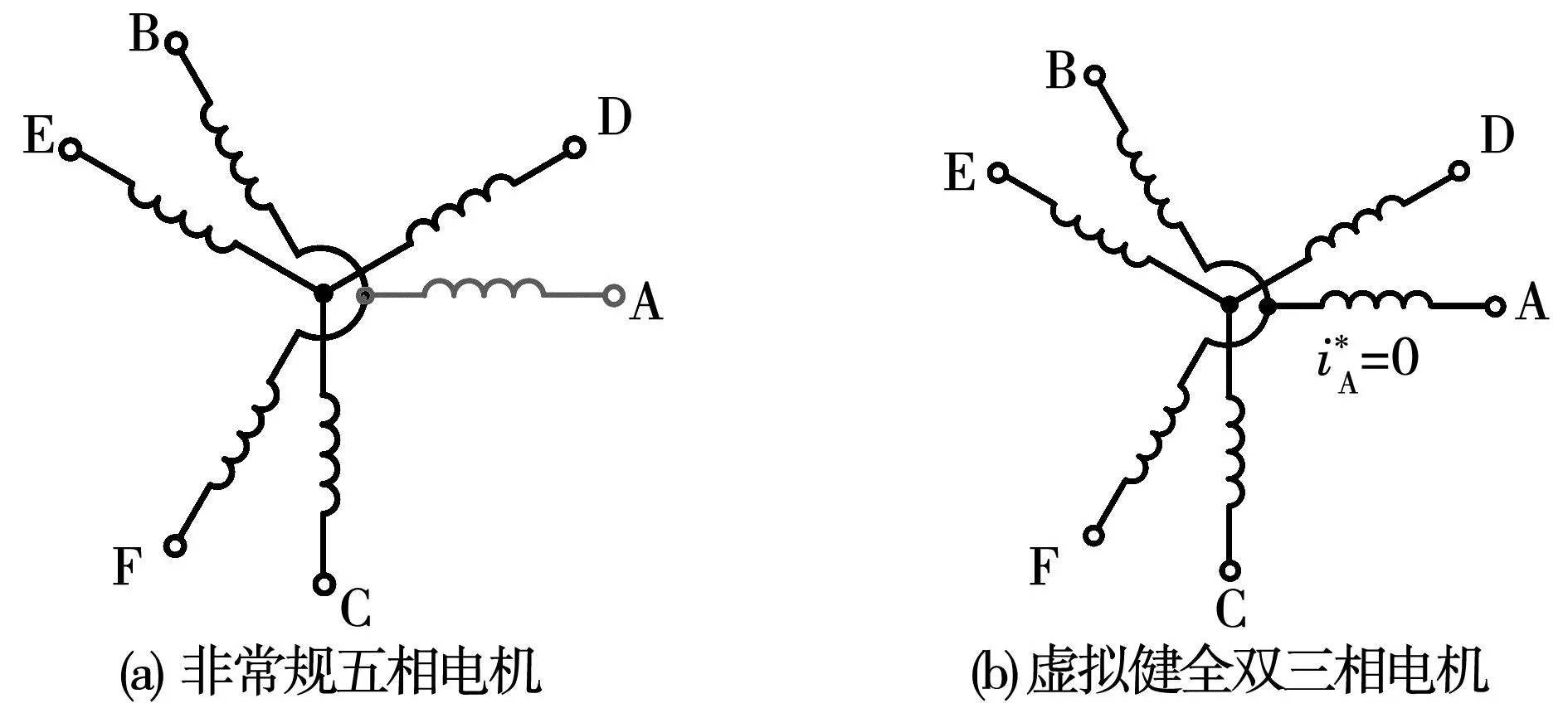
图2 双三相缺相故障Fig.2 Open-phase fault in dual three-phase PMSM

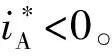
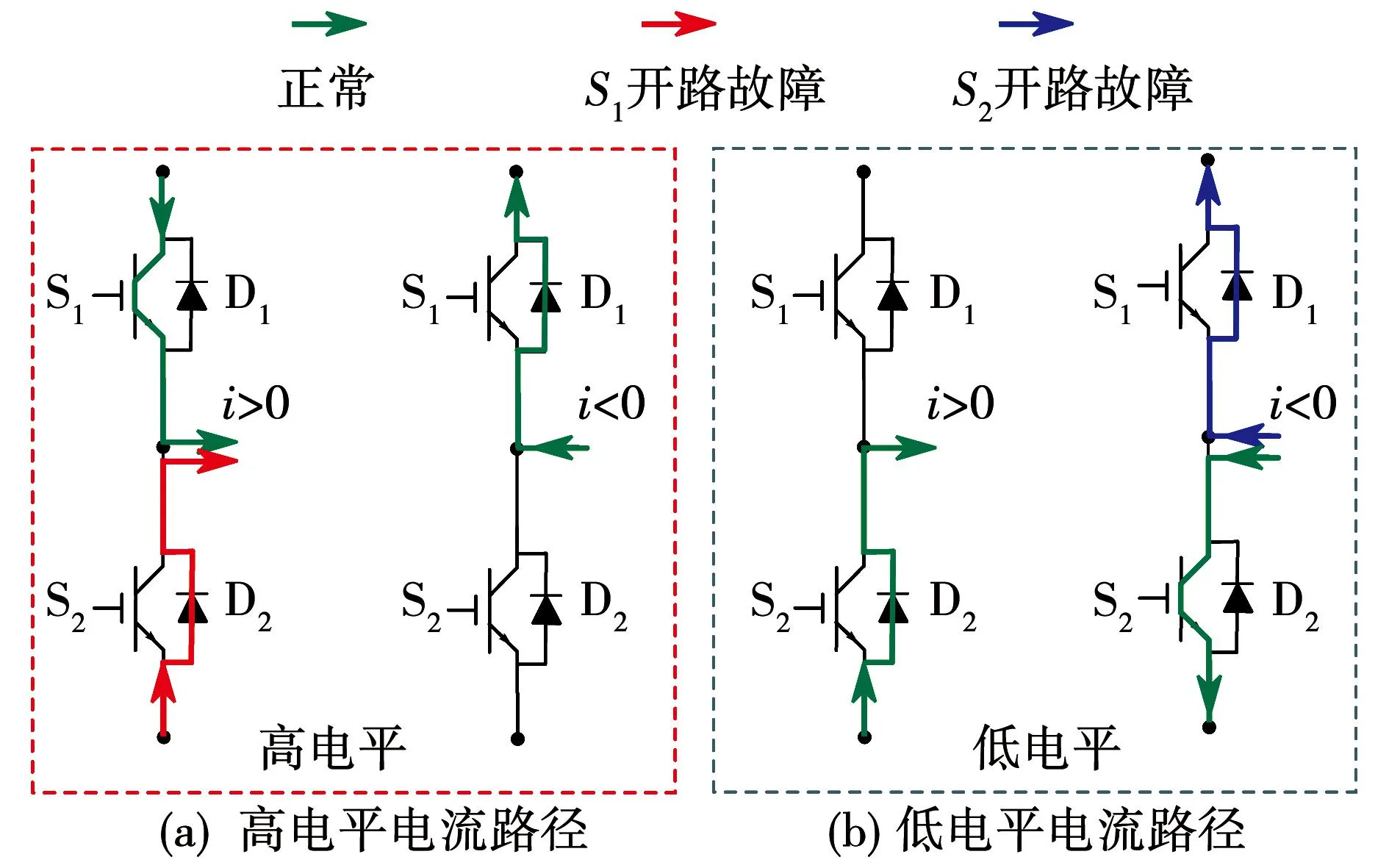
图3 开关管开路故障(正常)电流流通路径Fig.3 Current path under normal state and different fault states

综上所述,虚拟健全系统的核心在于将故障下的双三相电机驱动系统看作虚拟健全的双三相电机驱动,仅增加电流约束,不更改系统模型。

2.2 基于电流补偿的容错参考电流优化方法

双三相电机容错控制的基本目标为消除故障带来的转矩波动。本文通过电流补偿的方式建立等效旋转磁动势以实现容错运行下的平稳转矩输出。双三相电机ABC三相电流和DEF三相电流分别进行Clark变换到α1-β1和α2-β2坐标系,可表示为

(8)

基于式(3)、式(4)、式(8)可以得到正常运行下(id=0,ix=0,iy=0)双三相电机q轴电流和双坐标系下电流的关系:

(9)

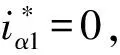
(10)

根据式(10)可以画出不同相缺故障下双三相电机的双α-β坐标系参考电流轨迹,如图4所示。图中绿色轨迹代表正常运行下的参考电流。红色轨迹FT-A代表A相缺相故障容错参考电流轨迹。FT-B至FT-F分别代表其他相的缺相故障下的容错参考电流轨迹。从图4中可以看出,通过采用健全三相绕组对故障三相绕组的缺失电流进行补偿即可建立等效的旋转磁动势,实现缺相故障基于电流补偿容错控制。

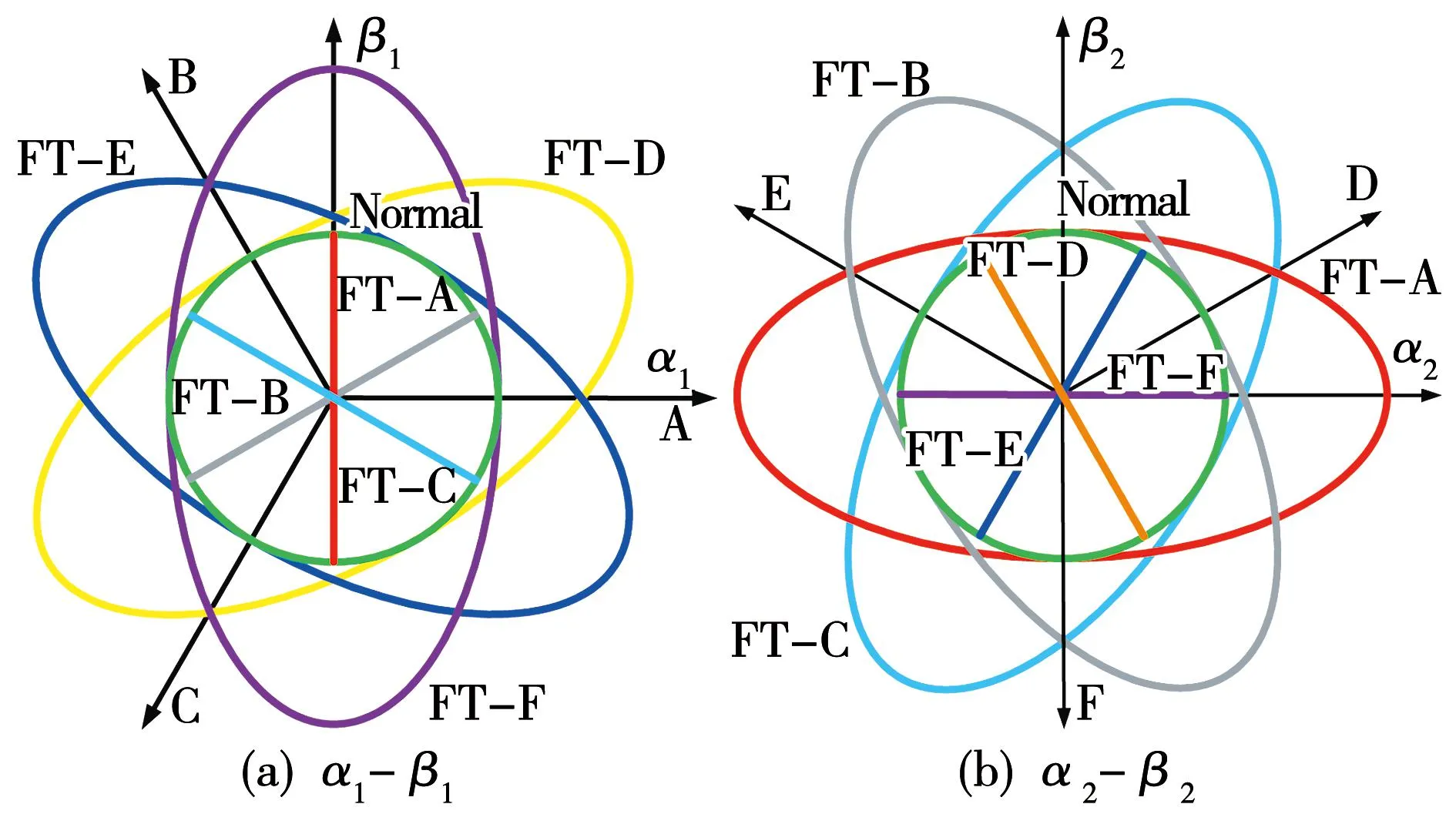
图4 双α-β坐系不同缺相故障基于电流补偿的容错参考电流轨迹Fig.4 Current compensation based fault-tolerant current reference trajectories of double α-β coordinate at different open-phase fault

结合式(3)和式(8)分别进行逆变换,可得双坐标系和解耦坐标系下的变换矩阵:

(11)

结合式(4)、式(10)、式(11)可得到x-y平面的参考电流:

(12)

对于变换器A相桥臂S1开关管开路故障,同样采用上述分析方法,可以得到容错下的x-y平面的参考电流如下:

(3)

变换器A相桥臂S1开关管开路故障基于电流补偿容错控制下的双坐标系参考电流轨迹如图5所示。通过对比式(12)和式(13)可知,采用提出的开关管开路故障基于电流补偿容错控制方法可进一步降低电机铜耗,提升转矩输出能力。

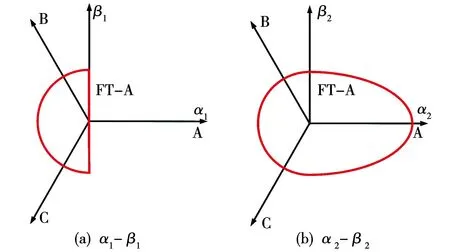
图5 双α-β 坐标系A相S1开关管开路故障基于电流补偿容错参考电流轨迹Fig.5 Current compensation based fault-tolerant current reference trajectories of double α-β coordinate under S1 open-switch fault in Phase-A

2.3 基于最小铜耗的容错参考电流优化方法

双三相电机容错控制的目标除了平稳转矩,还可以降低绕组铜耗。双三相电机绕组总铜耗为

(14)

因电机各相绕组均匀分布,故各相绕组电阻均为R,T为基波电流周期。同样以A相缺相故障(iA=0) 为例,来分析容错控制下的参考电流。为简化分析对参考值进行标幺化,以iq为基值,故iq(pu)=1, 由式(12), 可得A缺相故障iy=0, 再联合式(3)的逆变换和式(14),可得到仅由id的表达的铜耗为

(15)

以式(15)中PCu最小为优化目标,通过优化id电流波形,可得到双三相电机故障下绕组总铜耗最小的参考电流,具体优化分析如下。f(id)满足式(16),即对每个θe,存在id使f(id)最小。

∀θe∈(0,2π),∃id∈(-1,1)⟹minf(id)。

(16)

如果满足每个θe的最小f(id),则PCu必然最小。把(0,2π)区间n-1等分,横坐标对应θk(k=1,2,…,n),对每一个θk(常数),f(id)仅仅是关于id表达式,id从-1开始到1结束,每次增加一个较小的偏移量δ,如果f(id)变小更新idk。通过在区间(-1,1)遍历搜索,求出f(id)最小值对应的idk。即可求出最小铜耗下全局最优的id离散曲线。再根据数据点(θk,idk),进行曲线拟合,可得到近似的最小铜耗id表达式。A相缺相故障最小铜耗下的容错参考电流如下:

(17)

从图6可知,拟合的最小铜耗表达式的曲线几乎和离散的最小铜耗离散数据点重合。本研究以隐极式永磁同步电机为研究对象,故d轴电感Ld和q轴电感Lq相等。根据式(7)可知转矩Te=3neψfiq,因此在隐极式电机中id不影响转矩的波动,转矩由iq决定,而id的变化仅影响铜耗。通过优化电流id波形来实现定子绕组总铜耗最小,同时保持iq为恒定值,便可实现双三相电机转矩平稳运行。对于A相桥臂S1开关管开路故障最小铜耗容错控制参考电流优化方法,可参照开关管开路故障基于电流补偿容错控制下的参考电流优化方法相同思路进行设计,此处不再赘述。

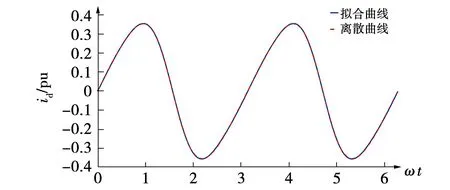
图6 最小铜耗下的离散曲线和拟合曲线Fig.6 Discrete curve and fitting curve with minimum-copper-loss constraint

2.4 非常规电流控制器

容错运行下的非常规参考电流对电流控制提出了更高的要求。传统的PI控制器,能有效跟踪直流信号,对非常规的容错电流无能为力。无差拍控制器能较好地跟踪非常规电流,但是依赖控制系统数学模型。滞环控制器具有较快的响应速度,但是控制精度较低,对采样时间有较高的要求。为了对周期性输入信号进行高精度的有效跟踪,日本学者Inoue等人首次提出了重复控制[14]。除此之外,重复控制能有效地抑制干扰信号,且不依赖控制系统数学模型。因此重复控制非常适合双三相电机系统容错运行的周期性非常规电流跟踪。本文采用改进型重复控制如图7所示,其中:W(s)为低通滤波器;τd为跟踪周期电流的周期;Gc(s)为动态补偿器也称为稳态补偿器。

图7 重复控制器Fig.7 Repetitive controller

重复控制器的核心主要是内模模型的应用[15],内模模型的零极图如图8所示[16]。内模模型在虚轴上的零点jkωτd(k=0,±1,±2,±3,…)正好可以对消跟踪的周期信号的极点。因此对角频率为ωτd或ωτd角频率的倍频周期信号都能进行有效的无静差跟踪。那么对于式(17)中的最小铜耗下的容错参考电流可实现有效跟踪。实际重复控制的作用效果和无穷多个比例谐振控制器(谐振频率jkωτd;k=0,±1,±2,±3,…)并联的效果类似,但只需要一个控制器便可实现多个频率信号的有效跟踪。

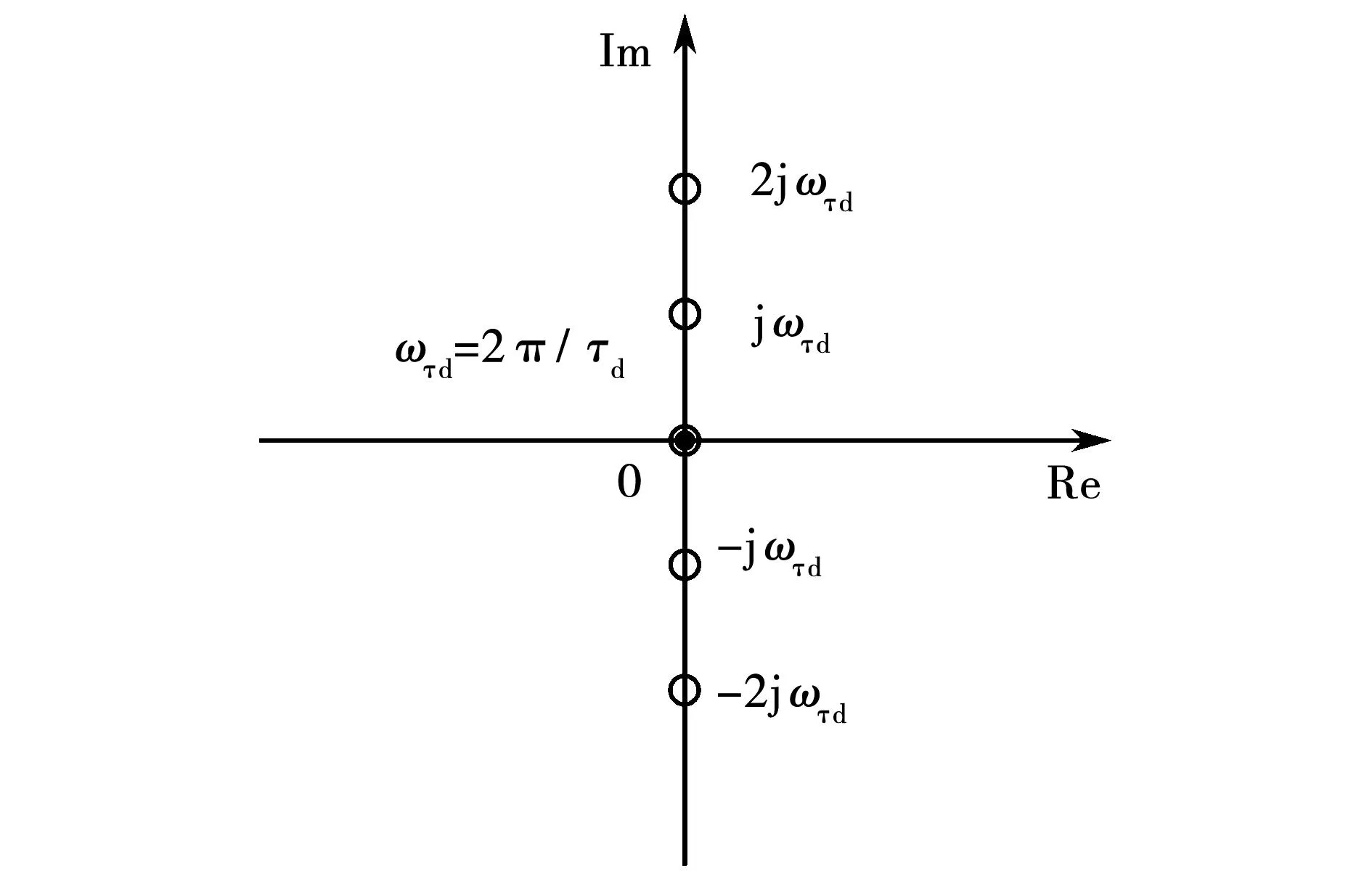
图8 内模模型零极图Fig.8 Zero-pole plot of the internal model

2.5 统一容错控制架构

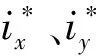
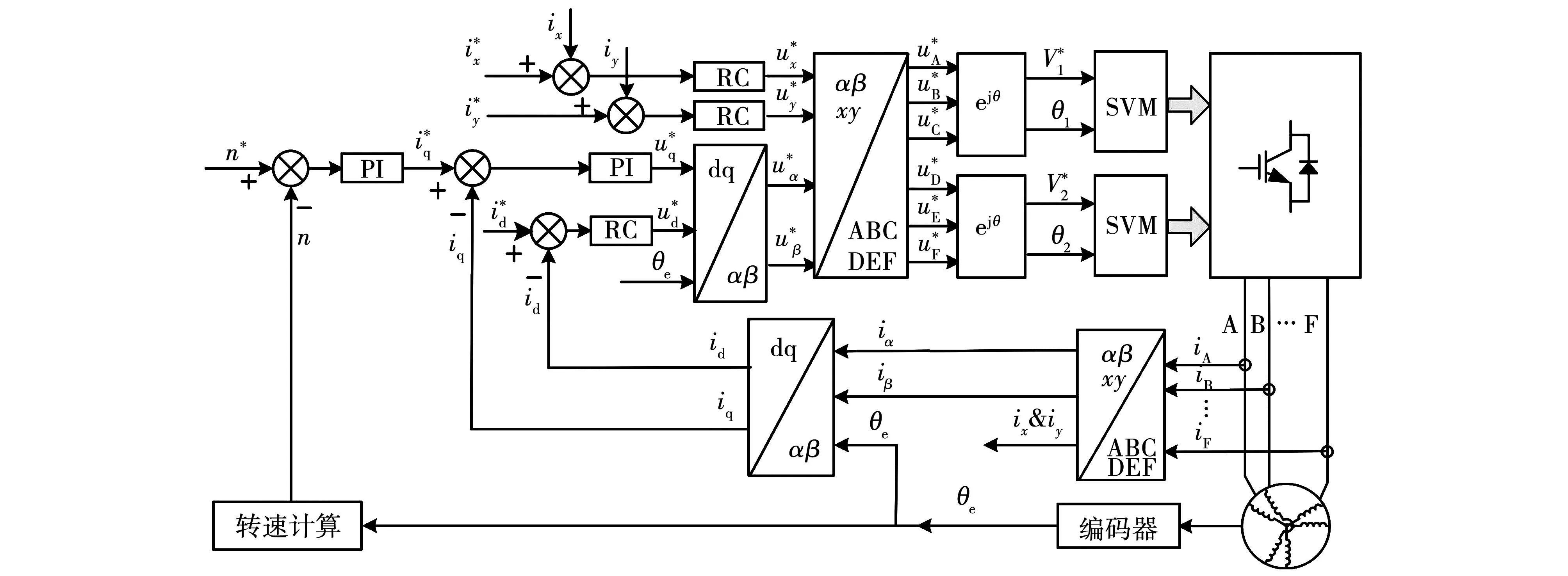
图9 双三相PMSM容错统一控制框架Fig.9 Universal fault-tolerant control framework of dual three-phase PMSM drive

3 实验结果

为了验证提出容错控制方法的有效性,分别对双三相永磁同步电机驱动系统缺相故障和开关管开路故障下的基于电流补偿容错控制和最小铜耗容错控制进行实验验证,实验测试平台如图10所示,其中实验参数如表1所示。

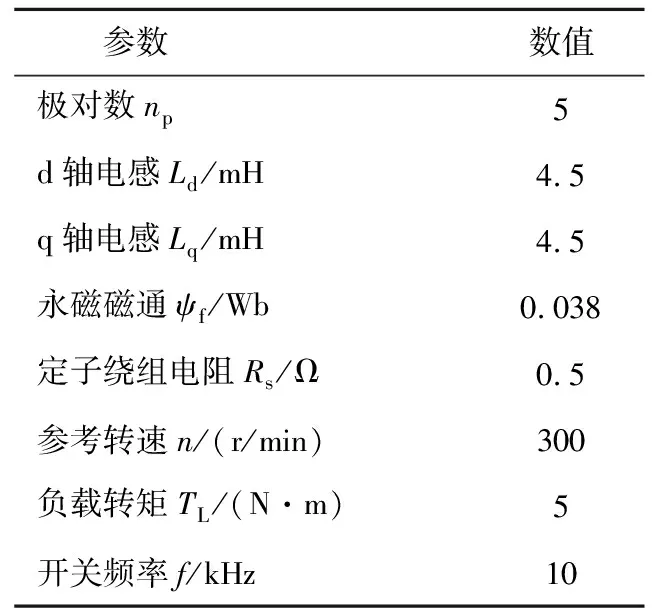
表1 实验参数Table 1 Experimental parameters

图11为A相缺相故障下基于电流补偿容错控制实验波形。图11(a)中,A相缺相故障导致A相电流为0,在电流闭环控制下其他相电流都有较高的正弦度。由DEF相绕组电流补偿,DE相的电流大于B相电流,和前述的理论分析一致。图11(b)和图11(c)中,d-q-x-y轴电流均能进行无静差的有效跟踪,尤其是x轴的正弦信号,采用重复控制可实现无静差有效跟踪。从图11(d)中可以看出容错运行下的转矩输出平稳,转速波动小。验证了缺相故障下基于电流补偿容错控制方法实现平稳转矩有效性。

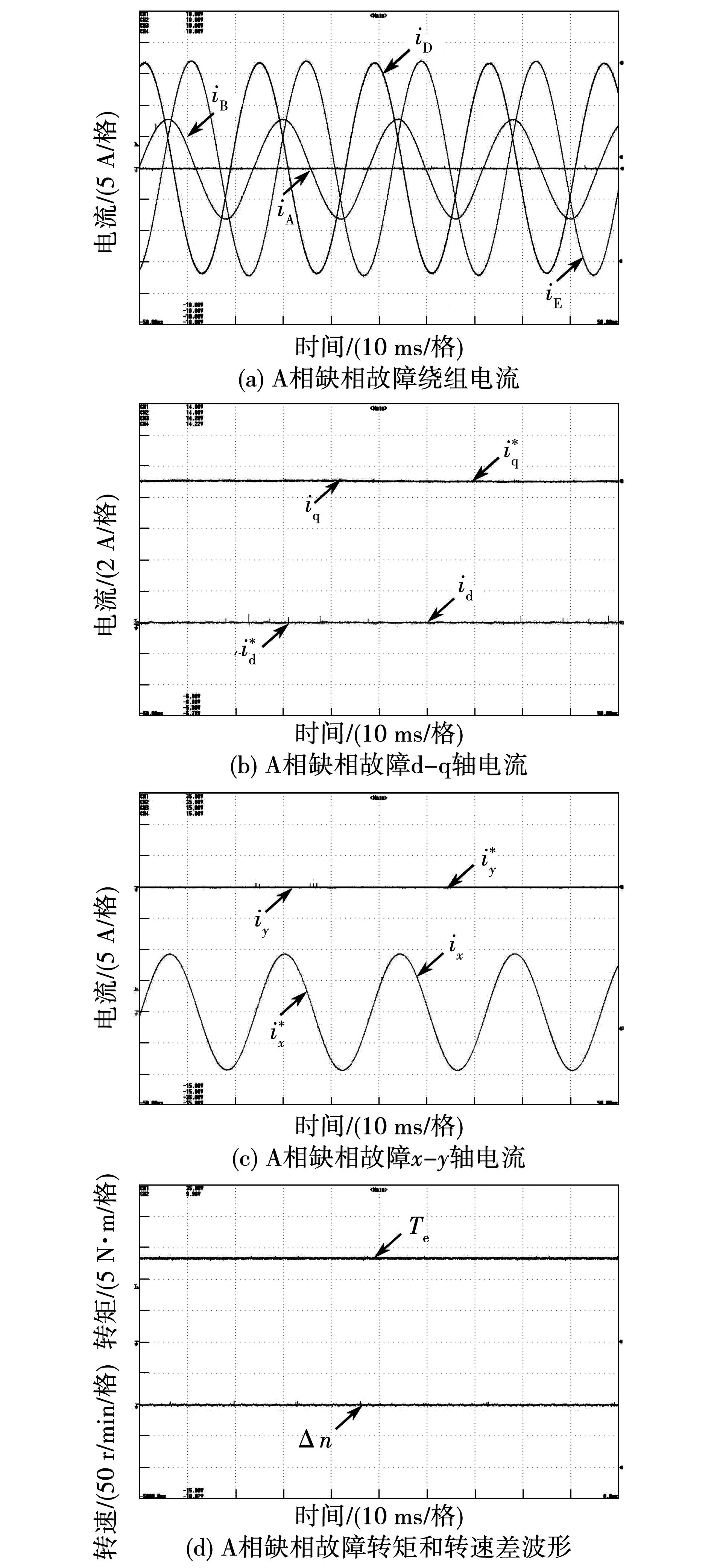
图11 A相缺相故障容错基于电流补偿容错控制实验波形Fig.11 Phase-A open-phase experiment waveform with current compensation based fault-tolerant control

图12为A相S1开关管开路故障基于电流补偿容错控制实验波形。由图12(a)可知,相电流在两个模态之间交替切换。对比图11(a),可以发现DE的电流峰峰值显著降低,得益于充分利用故障桥臂剩余的健全开关管。开关管故障容错运行下半个基波周期处在缺相容错运行模式,半个基波周期处在正常运行模式。图12(b)和图12(c)中,重复控制依旧能够确保直流信号及x轴的非常规周期信号的有效闭环跟踪。图12(d)中,容错运行下转矩输出平稳,转速波动小。

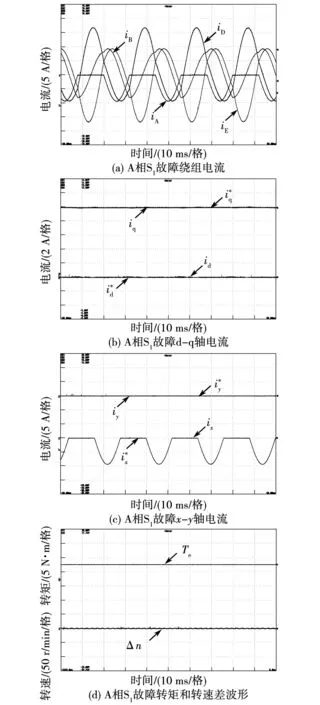
图 12 A相S1故障基于电流补偿容错控制实验波形Fig.12 Phase-A S1 open circuit experiment waveform with current compensation based fault-tolerant control

图13为A相缺相故障最小铜耗容错控制实验波形。图13(a)可知,DE相电流幅值大于B相电流。图13(b)和图13(c) 中,d-q-x-y轴电流均能有效跟踪其给定的最小铜耗参考电流。对d轴和x轴非常规电流信号闭环控制采用重复控制器,依旧实现高精度控制。从图13(d)中可以看出,采用提出的最小铜耗容错控制方法可确保容错运行下转矩和转速的平稳输出。

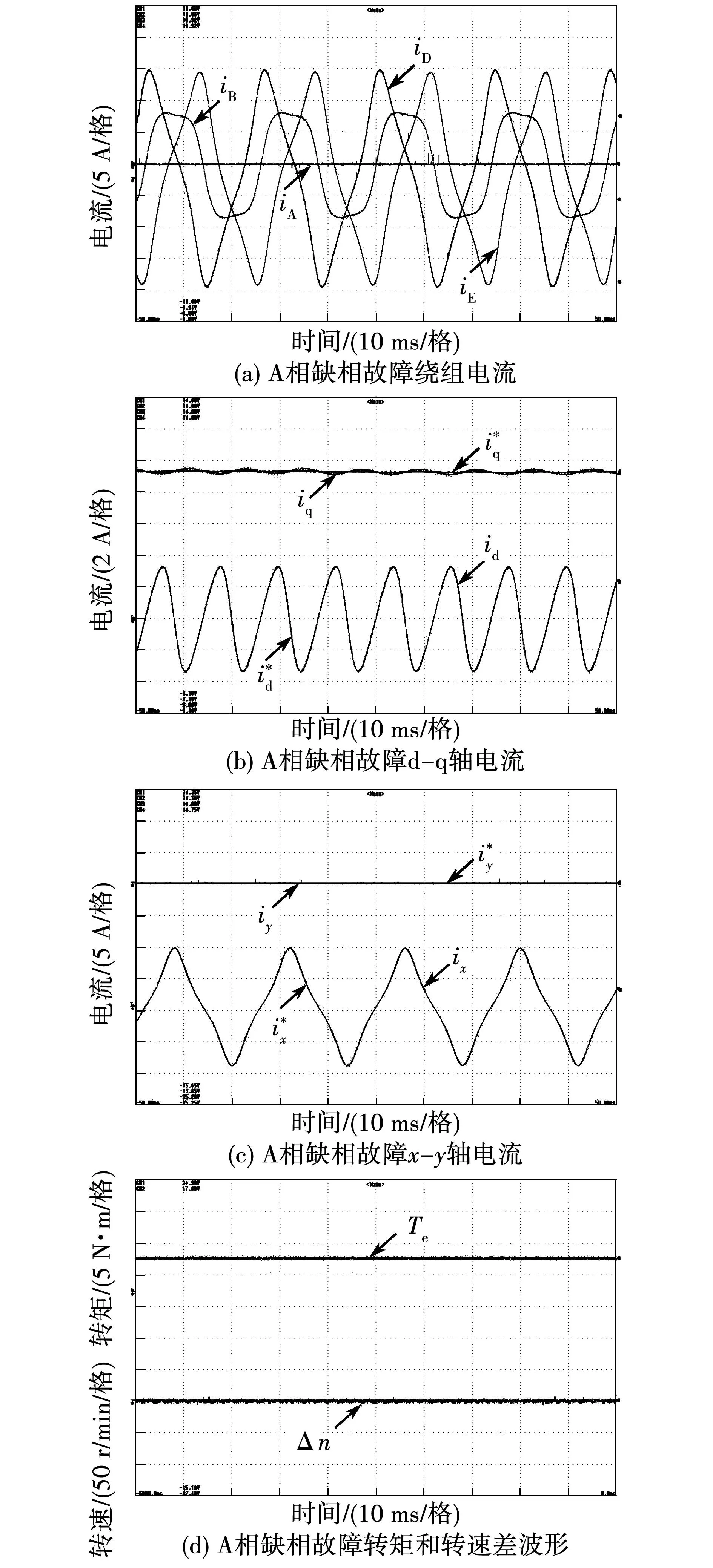
图13 A相缺相故障最小铜耗容错控制实验波形Fig.13 Phase-A open-phase experiment waveform with minimum-copper-loss control

图14为A相S1开关管开路故障最小铜耗控制实验波形。图14(a)中,各相电流在最小铜耗缺相运行模式和正常运行模式之间交替切换。从图14(b)和图14(c)可以看出重复控制器能确保给定开关管开路故障最小铜耗容错控制下非常规参考电流的有效跟踪。最终得以实现转矩和转速的平稳输出,如图14(d)所示。

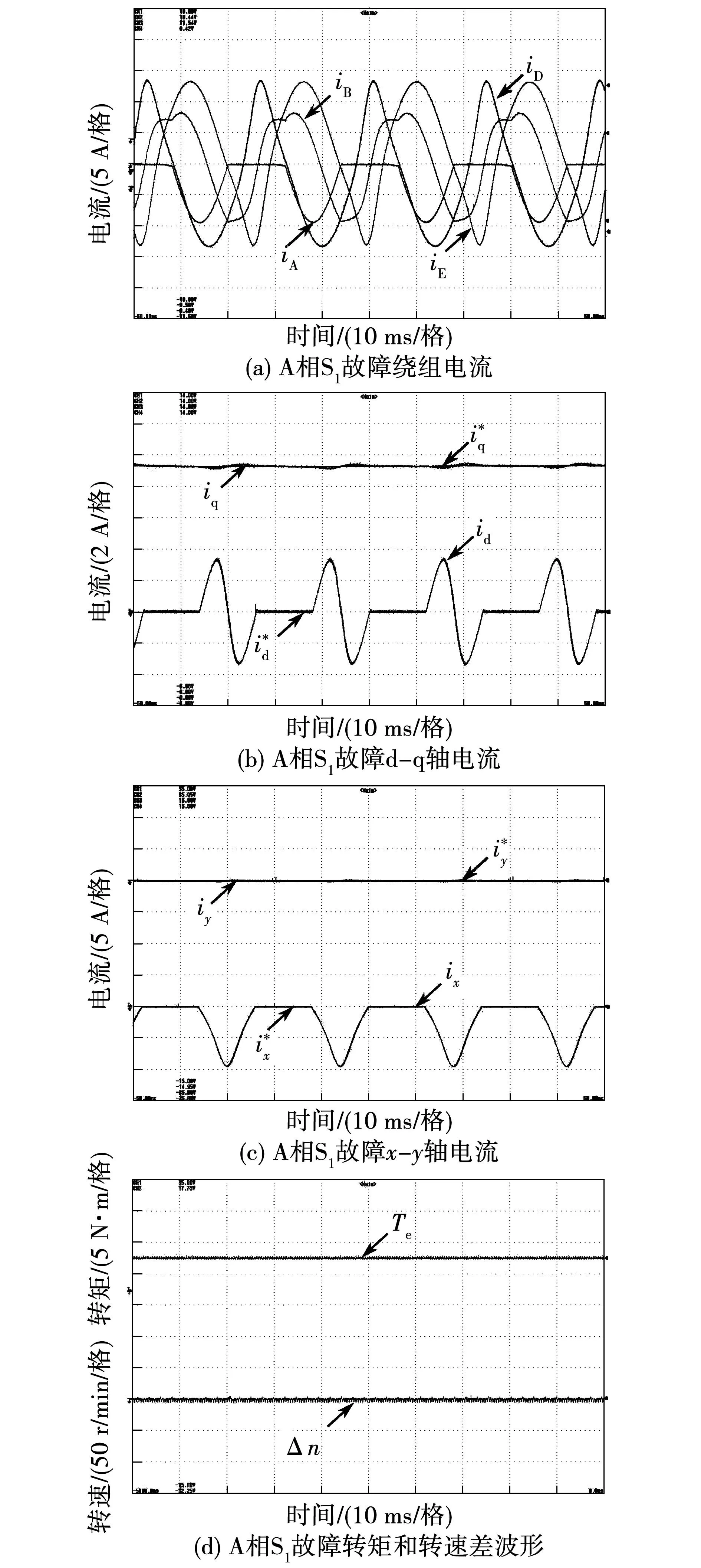
图14 A相S1故障最小铜耗控制实验波形Fig.14 Phase-A S1 open-circuit experiment waveform with minimum-copper-loss control

4 结 论

本文以双三相电机永磁同步电机驱动系统为研究对象,提出了一种开路故障简易容错控制方法,提出方法在开路故障前后无须改变系统的控制框架、调制策略、电机数学模型,仅更改电流参考值即可实现容错控制,降低了容错控制的复杂度。本文还提出了基于电流补偿参考电流优化和基于最小铜耗参考电流优化两种电流优化控制方法。在开关管开路故障下,通过充分利用故障桥臂健全开关管可进一步降低容错运行铜耗。论文实验结果充分验证了提出容错控制方法的有效性。