含大范围参数四维混沌系统的吸引子共存

颜闽秀， 朱君洋

沈阳化工大学信息工程学院，辽宁沈阳 110142

随着时间的推移，混沌系统得到了更深入的研究和发展.混沌系统具有遍历性、伪随机性，以及对初始条件的敏感性等特点，因此在随机数发生器［1-2］、图像加密与隐藏［3-5］，以及保密通信［6-8］等领域都得到广泛应用.与此同时，人们对组成简单、动力学特性复杂、伪随机性更高的混沌系统的需求日渐增加，因此，具有多种吸引子共存和超大范围参数混沌的系统得到了研究人员的广泛关注.

大范围参数混沌指混沌系统在较大参数的改变下，依然能够保持混沌状态.这种现象能够避免混沌系统在实际应用中因干扰导致参数改变，进而引起混沌状态改变，这极有利于混沌的应用.徐昌彪等［9］提出的基于Lorenz 系统的三维（threedimension， 3D）混沌系统，虽然构成简单，仍能在参数超大范围变化时保持混沌.张泽峰等［10］构建了一个五维保守超混沌系统，在保持Hamilton能量保守的同时，打破了系统的Casimir 能量保守，该系统在参数Π2处于［0， 1 600］变化时，仍始终处于超混沌状态.XIAN 等［11］提出了一个大范围参数三维连续混沌系统，并通过拓扑马蹄验证其混沌性.HUANG 等［12］设计了一种离散忆阻混沌映射，并通过数学证明新映射在一定条件下，可以处于无限宽范围参数混沌.

近年来，吸引子共存现象作为混沌系统的热点备受关注.吸引子共存指固定系统参数并改变系统初始值时，系统会随着不同初值进入不同轨迹，产生多种吸引子存在的现象.当一个混沌系统具有吸引子共存时，表明该混沌系统可能存在复杂的动力学特性.颜闽秀等［13］将双曲正切函数引入三维混沌系统，使系统出现数量可调节的吸引子共存.张贵重等［14］利用磁控忆阻器构建了一个五维忆阻混沌系统，并通过改变忆阻初始条件实现无穷多共存吸引子的超级多稳定.秦铭宏等［15］改变初始值，观察到共存的无穷多形态各异的吸引子.曹可等［16］利用磁控忆阻器作为负反馈，构造了一个新的四维（four-dimension， 4D）忆阻混沌系统，该系统在不同初始条件和参数下，有多种吸引子共存.尽管已有针对吸引子共存的混沌系统的研究，但对于同时具有大范围参数的混沌系统报道仍然较少，而使用参数控制吸引子在相空间中缩放的就更为少见，这些现象都表明混沌系统具有复杂特性.因此，研究此类混沌系统具有重要的现实意义.

本研究提出了一个改进的四维混沌系统，并分析该系统的动力学行为，通过改变系统的初值，研究新系统的吸引子共存现象；又通过调整系统参数，研究了参数对吸引子在相空间中的缩放控制作用.对新系统设计偏移升压控制器［17］，证明系统在实际应用中有较大潜力.最后，使用美国国家标准与技术委员会（National Institute of Standards and Technology， NIST）发布的软件包对新系统进行NIST测试［18］，验证了新系统具有良好的伪随机性，在图像加密与保密通信中有应用价值.

1 新四维混沌系统

YANG等［19］提出的三维混沌系统为

其中，x、y和z为状态变量；a、b和c为系统参数；、̇和̇为状态变量对时间的导数.

该系统属于Lorenz 和Chen 系统的中间过渡态.本研究基于此系统提出新的四维混沌系统，为

其中，w和k分别为新增的状态变量和系统参数；ẇ为w对时间的导数，k= 0.1 × 10-n-m× 10-2-n，n= 0， 1，…， ∞，m= 0， 1， 2， …， 8，且一直循环，每当m由8变为0时，令n=n+ 1，达到的效果为k从0.1 开始递减，即k =0.1，0.09，0.08，…，0.01，0.009，0.008，…，0.001，0.0009，…，最后无限趋近于0，即k∈（0， 0.1］.系统（2）中的系统参数与系统（1）中的参数均不相同.当a= 1，b= 3，c= 2，k= 0， 初值为(x0，y0，z0，w0)=(2，1，2.5，1)时，系统（2）吸引子如图1.

图1 新混沌系统（2）的吸引子图 （a）x-y相图； （b）x-z相图； （c）x-w相图； （d）y-z相图Fig.1 Attractor diagram of the new chaotic system (2). (a) x-y phase diagram, (b) x-z phase diagram, (c) x-w phase diagram and(d) y-z phase diagram.

2 基本动力学特性

2.1 Lyapunov指数和分维数

当a= 1，b= 3，k= 0，系统初值（x0，y0，z0，w0） = （2， 1， 2.5， 1）时，计算得到新系统的李雅普诺夫（Lyapunov）指数为L1= 0.155，L2= 0，L3=-2.002，L4= -2.154，这4个Lyapunov指数的数值符合(+，0，-，-)的规律，证明新系统是一个四维混沌系统.这4 个Lyapunov 指数之和LSE＜ 0，说明新系统为耗散系统.此时，Lyapunov维数为

其中，j满足且

由式（3）可得DL= 2.078.由于2 ＜DL＜ 3，证明系统（2）为混沌系统.

2.2 对称性和耗散性

系统（2）在（x，y，z，w）坐标变换到（-x， -y，z，w）坐标时，状态方程保持不变，说明系统（2）关于z-w平面对称.

系统（2）的耗散性公式为

因此，当系统参数a= 1，b= 3，c= 2，k= 0时，有-(a+b) +k＜0，表明该系统为耗散系统.

2.3 平衡点分析

计算系统的平衡点，令式（2）左边都为0，即

当a= 1，b= 3，c= 2，k= 0，系统初值(x0，y0，z0，w0)=(2，1，2.5，1)时，系统的平衡点为P1（0， 0， 0， 0）、P2（4， -2， -2， 2）和P3（4， 2，2， 2）.新系统的Jacobian矩阵为

当平衡点为P1时，求得特征值λ1= 1，λ2=-1，λ3=λ4=-2，可见4 个根都为实数，且λ1＞0，λ2、λ3和λ4都小于0，说明平衡点P1为指标为1的鞍点，该鞍点用来连接涡卷与涡卷之间的键带.

当平衡点为P2时，求得特征值λ1= 1.629 +2.007i，λ2= 1.629 - 2.007i，λ3= - 3.629 +2.189i，λ4= - 3.629 - 2.189i， 对应的实部Re(λ1) ＞0、 Re(λ2) ＞0、 Re(λ3)＜0且Re(λ4) ＜0，说明平衡点P2为指标为2的鞍焦平衡点，用来生成涡卷.当平衡点为P3时，求得特征值λ1= 1.43 +2.325i，λ2= 1.43 - 2.325i，λ3= -3.43 + 2.325i，λ4= - 3.43 - 2.325i，可见平衡点P2为指标为2 的鞍焦平衡点，也是用来生成涡卷的.由图1 可见，新系统依据平衡点的类型生成了2 个涡卷和1 个连接它们的键带.

2.4 0-1测试

使用0-1 测试［20］进一步验证新系统的混沌性.当a= 4.5，b= 4.9，c= 2，k= 0，系统初值为（x0，y0，z0，w0） = （2， 1， 2.5， 1）时，（p，s）平面如图2（a）.其中，p和s分别为关于l的函数

图2 0-1测试的(p，s)图 （a）a = 4.5， b = 4.9， c = 2，k = 0；（b）a = 1，b = 3，c = 2，k = 0Fig.2 (p, s) diagram of 0-1 test. (a) a = 4.5, b = 4.9, c = 2,k = 0 and (b) a = 1, b = 3, c = 2, k = 0.

其中，ϕ(m) 为可观测数据集；θ(m)=mδ+为任意常数，δ∈R+.

由图2（a）可清楚地看到，系统现状态为周期或拟周期，计算得到此时Lyapunov 指数为L1= 0，L2= -0.195，L3= -4.494，L4= -4.710，能够证明系统处于周期状态.而后修改系统参数，保持初值不变，当a= 1，b= 3，c= 2，k= 0时，系统处于混沌状态，系统的0-1测试结果如图2（b），符合混沌状态时的轨迹.

3 参数对新系统的影响

3.1 大范围混沌现象

改变系统参数会影响整个系统的混沌特性，通过对分岔图和Lyapunov指数图的分析，能够深入了解混沌系统各个状态下的不同性质.

当a= 1，c= 2，k= 0，系统初值（x0，y0，z0，w0）=（2， 1， 2.5， 1）时， 可得改变b的值（b∈(1，6)）时系统的分岔图如图3.由图3 可见，当b∈(2.1，4.8)时，分岔图上面的点是大量且密集的，这时新系统处于混沌状态.而当b＞4.8后，系统出现了明显的反倍周期分岔现象.

图3 参数b改变时系统（2）的分岔图Fig.3 Bifurcation diagram of system (2) when changing parameter b.

在不改变系统参数和初值的情况下，令b∈(1，6)，得到Lyapunov指数图如图4（a）.由图4（a）可见，当b= 3 时，系统处于混沌状态.当b∈(2.1，4.8) 时，系统的Lyapunov 指数符合(+，0，-，-)，说明此范围内系统（2）处于混沌状态，与分岔图分析一致.随着系统参数b的增大，L3和L4都在逐渐减小，这意味着Lyapunov指数和将会越来越小.

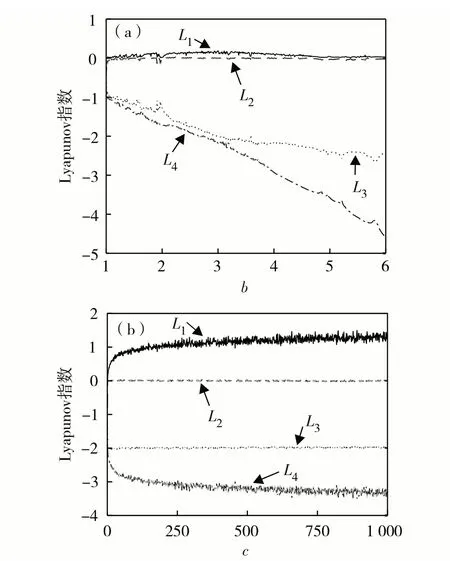
图4 （a）b ∈（1， 6）和（b）c ∈（0， 1 000）条件下的Lyapunov指数图Fig.4 Lyapunov index chart on (a) b ∈ (1, 6) and(b) c ∈ (0, 1 000).

当a= 1，b= 3，k= 0，系统初值(x0，y0，z0，w0)=(2， 1， 2.5， 1)时， 令c∈ （0， 1 000），得到Lyapunov指数图如4（b）.此时的Lyapunov指数一直保持L1＞0、L2= 0、L3＜ 0和L4＜ 0，且L1和L2的图像与L3和L4的图像关于c= -1对称，表明系统（2）具有大范围混沌特性.实际上当c= 1 × 104时，系统（2）的Lyapunov 指数L1＞ 0、L2= 0、L3＜ 0、L4＜ 0，系统仍处于混沌状态，因此可说新系统存在大范围参数混沌特性.

3.2 共存吸引子

固定系统参数，通过改变系统初值，则会出现不同独立的吸引子属于吸引子共存.令系统参数保持不变，控制改变系统初值来观察吸引子共存，得到系统的相图如表1和图5.

图5 参数固定不同系统初值的x-w平面相图 （a）（x0， y0， z0， w0） = （2， 1， 2.5， 1）， （a， b， c， k）=（2， 4.9， 2， 0）； （b）（x0， y0，z0， w0） = （-2， -1， -2.5， 1），（a， b， c， k） = （2， 4.9， 2， 0）； （c）（x0， y0， z0， w0） = （-1， 1， 3， 1），（a， b， c， k） = （2， 5.8， 2， 0）；（d）（x0， y0， z0， w0） = （2， 1， 3， 1），（a， b， c， k） = （2， 5.8， 2， 0）； （e）（x0， y0， z0， w0） = （-2， 1， 2.5， 1）， （a， b， c， k） = （2， 3， 2，0）； （f）（x0， y0， z0， w0） = （2， 1， 2.5， 1）， （a， b， c， k） = （2， 3， 2， 0）Fig.5 x-w plane phase diagram with fixed parameters for different initial values of the system. (a) (x0, y0, z0, w0) = (2, 1, 2.5, 1), (a, b, c,k) = (2, 4.9, 2, 0), (b) (x0, y0, z0, w0) = (-2, -1, -2.5, 1), (a, b, c, k) = (2, 4.9, 2, 0), (c) (x0, y0, z0, w0) = (-1, 1, 3, 1), (a, b, c, k) = (2, 5.8, 2,0), (d) (x0, y0, z0, w0) = (2, 1, 3, 1), (a, b, c, k) = (2, 5.8, 2, 0), (e) (x0, y0, z0, w0) = (-2, 1, 2.5, 1), (a, b, c, k) = (2, 3, 2, 0), and (f) (x0, y0, z0,w0) = (2, 1, 2.5, 1) (a, b, c, k) = (2, 3, 2, 0).

3.3 系统伸缩系数k

不再令k= 0，而是按照k= 0.1 × 10-n-m×10-2-n的规则使k依次递减，选取有代表性的k值所对应的相图及Poincare截面图，观察随着k的减小，吸引子在相空间中的变化.图6 是k为0.1、0.08、0.06、0.04、0.02 和0.008 时，系统（2）的y-z-w三维相图和z-w二维相图.由图6 可见，吸引子的体积与k值呈正相关.

图6 系统参数k减小时对应的（a）y-z-w三维相图和（b） z-w二维相图Fig.6 (a) The 3D phase diagram of y-z-w and (b) the phase diagram of z-w corresponding to the decrease of system parameter k.

为验证该现象并非偶然，又选取x-y-z三维相图（图7（a））和x-y二维相图（图7（b）），观察不同k值时相图的变化.通过图7（a）和（b）能够发现，吸引子的体积随着k值的减小缓慢减小，从二维相图中能够明显看到，不同的相图通过颜色的区分已经发生了分层.为使验证更具说服力，给出了当z= 4.5时的Poincare截面图，如图7（c）.由图7（c）可观测到，截面的图像随着k值的减小而缩小，说明吸引子的体积在变小.

图7 系统参数k减小时对应的相图以及Poincare截面图（a）x-y-z三维相图； （b）x-y二维相图； （c）z = 4.5时的Poincare截面图Fig.7 Phase diagram and Poincare cross-sectional view corresponding to the reduction of system parameter k. (a) The 3D phase diagram of x-y-z, (b) the phase diagram of x-y , and(c) Poincare cross-sectional view at z = 4.5.

随着k值的减小，发现吸引子体积并不会无限收缩，而是缩小至某一值后就保持不变.图8 为k减小时对应的y-z-w面和z-w面相图，图9 为k减小时对应的x-y-z面和x-y面相图以及z= 4.5时的Poincare截面图.由图8和图9（a）、（b）可见，选取不同的三维相图和二维相图，当k值达到0.001 时，吸引子体积就不再发生改变，由图8（b）可清楚地看到，当k= 1 × 10-3变换到k= 1 × 10-6时，吸引子相图依然没有缩小，而是保持不变，仅相图的运行轨迹不同，这种现象在图9（b）中也能清晰地观察到.另外，通过观察图9（c）中的Poincare 截面图，也能够看出相体积没有发生缩小.

图8 系统参数k减小时对应的（a） y-z-w三维相图和（b） z-w二维相图Fig.8 (a) The 3D phase diagram of y-z-w and (b) the phase diagram of z-w corresponding to the decrease of system parameter k.

3.4 系统复杂度

复杂度分析能够反映混沌系统的结构复杂度，在通信领域中系统复杂度与通信安全密切相关.本研究使用谱熵（spectral entropy， SE）对新四维混沌系统进行分析.

令系统初值（x0，y0，z0，w0）=（2， 1， 2.5， 1），参数a= 1，c= 3，k= 0 时，图10 给出了系统在b∈ ［1， 7］时的谱熵复杂度（E）.由图10 可见，SE的最大值（Emax）为0.8.对比本研究提出的系统（2）与近些年提出的5个较为先进的混沌系统［21-25］的复杂度，结果如表2.其中，文献［21］与文献［23］中的混沌系统都具有吸引子共存现象；文献［22］中的混沌系统有声学方面的应用；文献［24］与文献［25］中的混沌系统分别引入了三角函数和忆阻器.由表2可见，系统（2）的四维混沌系统的复杂度最高，在应用中有更大优势.

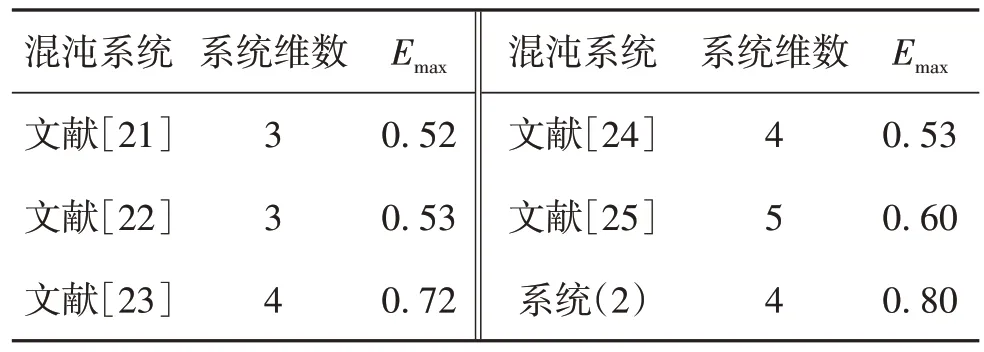
表2 不同混沌系统的复杂度对比Table 2 SE complexity comparison

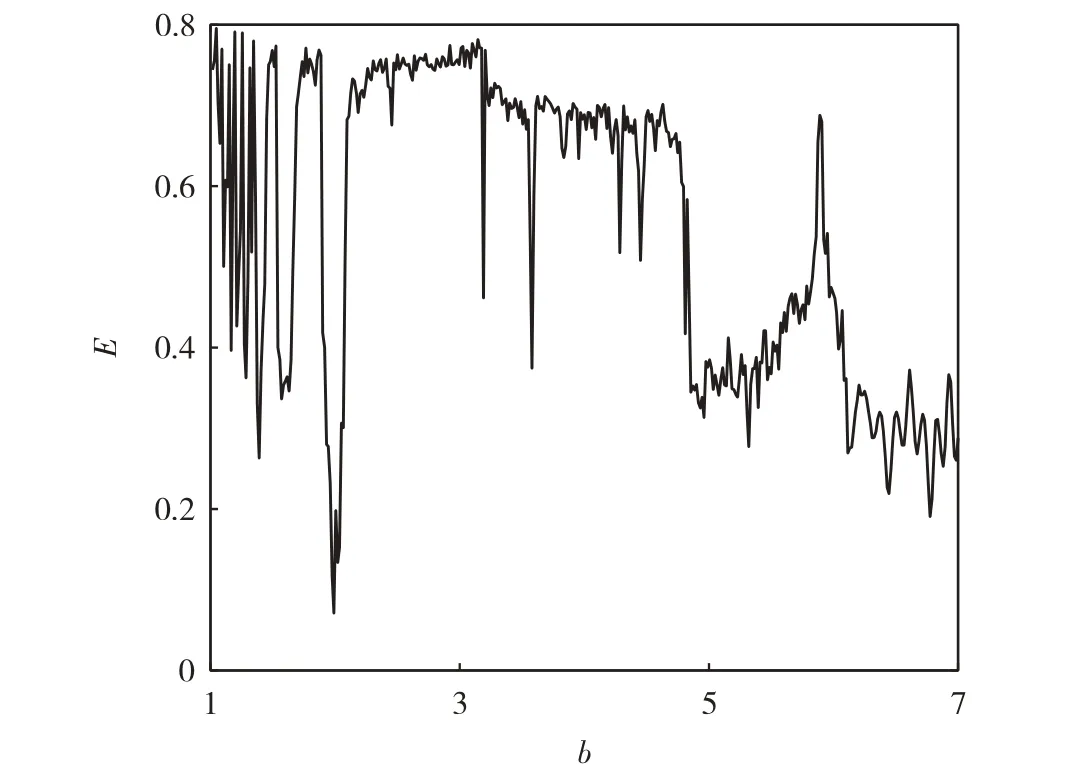
图10 随参数b变化的SE复杂度Fig. 10 SE complexity varying with parameter b.

4 偏移升压

近些年来，人们越来越重视混沌系统领域的应用，发现了一类能够通过控制混沌系统的状态变量来实现偏移升压，以此来改变自身信号的极性的系统.这类系统可将双极性信号改变为正的单极信号和负的单极信号，该类系统在工程应用时较传统混沌系统更加有利，能够通过改变信号的振幅来减少实际应用中器件的使用.本研究对系统（2）的状态变量y设置控制器进行控制.设n为偏移升压的控制器，将原状态变量y改为y+n，则新系统的状态方程（2）变为

令a= 1，b= 3，c= 2，k= 0，系统初值（x0，y0，z0，w0）= （2， 1， 2.5， 1），通过控制n的大小来观察信号的变化，结果如图11 所示.由图11 可见，当n= 0时，x-y平面的相图在中间位置（黑色），当n= 6 时，x-y平面的相图下移（红色），而当n=-6时，x-y平面的相图上移（蓝色）.从图11（b）可见，原始信号y为双极性，在控制n的改变后，信号y出现了正单极性和负单极性.

图11 改变控制器n的相图偏移变化及y信号极性改变（a）相图偏移变化； （b）y信号的时序图变化Fig.11 The phase diagram offset change and the polarity of the y signal change change the controller n. (a) The phase diagram offset varies and (b) the timing diagram of the y signal changes.

以上结果说明，引入偏移升压控制器，有利于新系统更好地适应实际应用.

5 NIST测试

美国国家标准与技术研究所制定的随机序列测试标准SP800-22 被称为NIST 测试，共包括15 项测试，若通过这些测试，则可说明混沌序列具有良好的伪随机性.测试结果均使用P值表示，P值越大越好，显著性指标α∈ ［0.001， 0.01］，本研究取α= 0.01.将P值与设置的α做对比，若P＞α则认为通过该项测试，反之，则不通过.按照NIST 测试的规定，被测序列的长度N要保证在1 × 103～1 × 107，本研究取N= 1 × 106，测试结果见表3.

表3 系统（2）的NIST测试结果Table 3 NIST test results for system （2）

由表3 可见，在系统（2）的NIST 测试结果中，P值全部大于显著性指标0.01，因此可以说明新系统（2）混沌序列有着良好伪随机性.

结 语

基于YANG 和CHENG 的三维混沌系统［19］提出一个新的四维混沌系统.对新系统进行对称性、耗散度、分维数、0-1 测试、平衡点、分岔图和Lyapunov指数的动力学分析，验证了新系统为四维混沌系统.通过观察参数c对系统的影响，验证了新系统具有超大范围参数的混沌特性，且当系统参数和初值发生改变时，出现吸引子共存的现象.观察新系统的相图和Poincare 截面图发现，通过改变伸缩参数k，能够控制混沌吸引子在相空间的大小，且当k趋于一定值后，吸引子的大小不再发生变化.谱熵计算结果说明系统具有较高的复杂度.设计新系统的偏置升压控制器，表明新系统具有工程应用价值.对新系统进行NIST 测试，结果表明，新系统具有良好的为随机性.本研究提出的新四维混沌系统在如伪随机发射器、图像加密等实际工程中的应用具有较大的潜在价值.