压缩浇筑混凝土的应力-应变关系

吴宇飞， 汪勋， 袁方， 胡彪

深圳大学土木与交通工程学院，广东省滨海土木工程耐久性重点实验室，广东深圳518060

低成本和原材料易获取使混凝土成为工程结构中应用最广泛的材料之一.几个世纪以来，学术界和工业界一直在努力改善混凝土的材料性能，以满足实际工程结构的力学性能和耐久性要求［1-7］.压缩浇筑技术在不改变混凝土配合比和不增加成本的情况下显著降低混凝土的孔隙率，进而大幅提升混凝土的强度和耐久性，近年来得到国内外学者越来越多的关注［8-15］.在压缩压力的作用下，混凝土中多余的水分和空气被挤压排出，内部孔隙率降低，粗细骨料被挤压密实，骨料之间的互锁效应增强，从而显著提高了混凝土的抗压强度和耐久性.图1为压缩浇筑混凝土浇筑过程示意.

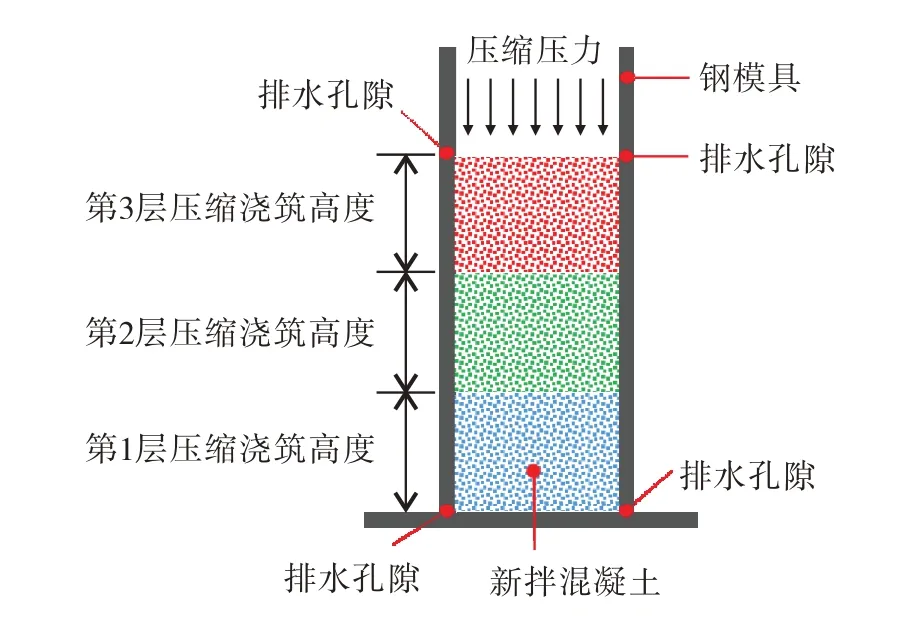
图1 混凝土压缩浇筑示意Fig.1 Schematic diagram of concrete compression casting.

压缩浇筑混凝土的本构关系是研究压缩浇筑混凝土构件和结构力学行为的基础，对理论分析结果能否准确反映结构实际受力情况有重要影响.然而，目前还未见利用压缩浇筑混凝土本构关系进行结构设计的相关研究报道.因此，本研究通过分析压缩浇筑混凝土的应力-应变关系，在现有混凝土应力-应变模型基础上修正参数，得到适用于压缩浇筑混凝土的应力-应变关系模型，并基于该模型推导压缩浇筑混凝土结构弯曲设计中所需的混凝土极限压应变εcu和等效矩形应力块系数，为压缩浇筑混凝土结构的抗弯设计和分析提供理论基础.

1 试验概况

本研究采用4种不同混凝土配合比试样，分别以C15、C20、C25 和C30 表示（表1）.混凝土采用双轴式搅拌机制备，试件尺寸均为150 mm（直径）× 300 mm（高度）的圆柱体.本研究分析水灰比、压缩压力p、压缩时间t和压缩高度h对压缩浇筑混凝土力学性能的影响.共设计15组试件，每组设置3个重复试件，如表2 所示. 试件编号中左边表示混凝土类型（NC为普通混凝土，其他为压缩浇筑混凝土），右边表示的是水灰比.对于压缩浇筑混凝土，H、P和T后面的数字分别表示的是压缩浇筑高度、压缩压力和压缩时间.例如，H300P15T0.5-0.53表示压缩浇筑高度为300 mm、压缩压力为15 MPa、压缩时间为0.5 min以及水灰比为0.53的压缩浇筑混凝土. 对于300 mm 高的圆柱体试件，当压缩浇筑高度为100 mm 时，分3 层压缩浇筑；当压缩浇筑高度为150 mm 时，分2 层压缩浇筑；当压缩浇筑高度为 300 mm时，分1层压缩浇筑，见图1.

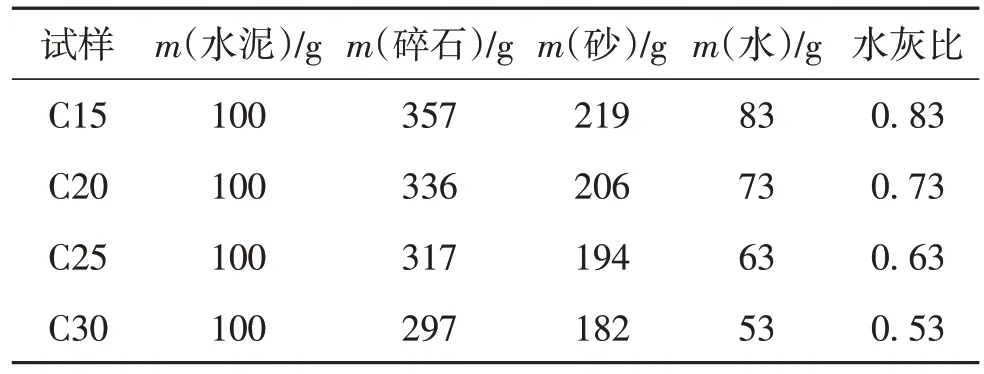
表1 混凝土配合比设计Table 1 Mixture proportions of concrete

表2 混凝土圆柱体试件及测试结果Table 2 Concrete cylindrical specimens and test results

2 试验结果

2.1 压缩浇筑混凝土力学性能

混凝土圆柱体试件及测试结果见表2.其中，fco为混凝土的抗压强度；为Ec弹性模量；εco为混凝土的峰值应力对应的应变.相比于普通混凝土，压缩浇筑混凝土的fco升幅达55.5%～89.0%，Ec升幅达38.1%～90.7%，εco减少了13.6%～32.3%.其中，当压缩浇筑高度分别为300、150 和100 mm时，fco最大提升率分别为74.2%、83.2% 和74.1%，压缩浇筑高度为150 mm 时，强度提升最大，但压缩浇筑高度为300 mm 时，压缩浇筑工作效率最高.当压缩压力分别为5、15 和25 MPa 时，fco最大提升率分别为66.3%、78.2%和59.4%，可见，压缩压力为15 MPa 时效果最佳.当压缩时间分别为0.5、2.0、10.0 和1 440.0 min 时，fco提升率分别为65.9%、75.5%、69.4%和88.0%.压缩时间为1 440 min 时，施工效率低.因此，采用压缩时间为2 min可以兼顾施工效率和强度提升效率.应当指出，不同压缩浇筑高度，压缩时间对施工效率影响较大，结合混凝土压缩浇筑效果及实际工作效率，建议最优的压缩浇筑高度为300 mm，压缩压力为15 MPa，压缩时间为2 min.

2.2 应力-应变曲线

图2 显示了所有混凝土试件的应力-应变曲线.由图2可见，当水灰比为0.53时，大多数压缩浇筑混凝土试件无法得到较为完整的应力-应变曲线的下降段，这主要是由于材料的脆性和试验压力机的刚度不足造成的，对于高强脆性混凝土这是常见现象［16-17］.从图2（a）可以看出，压缩浇筑高度对应力-应变曲线的影响不显著. 从图2（b）可以看出，当压缩压力为5 MPa时，测得应力-应变曲线下降段稍长.当压缩压力分别为15 MPa 和25 MPa 时，测得的应力-应变曲线下降段较短，且曲线形状较为陡峭，这主要是由于较大压缩压力的作用造成了混凝土材料较大的脆性. 由图2（c）可见，当压缩时间为0.5 min 时，测得的应力-应变曲线下降段最长，当压缩时间为1 440 min 时，测得的应力-应变曲线下降段最短.上述现象表明，在较大压缩压力和较长压缩时间下，压缩浇筑混凝土一般会表现出较大的脆性，这是混凝土内部骨料挤压程度造成的，混凝土越密实，强度提升程度越大，但是脆性也相对较大.图2（d）显示，当水灰比大于0.53 时，可以采集到压缩浇筑混凝土应力-应变曲线的下降段，这是由于混凝土的水灰比变大，强度较低，在相同的压缩压力作用下，混凝土仍然具有一定的延性.

图2 压缩浇筑变量对混凝土应力-应变曲线的影响 （a）压缩浇筑高度；（b）压缩压力；（c）压缩时间；（d）水灰比Fig.2 Effect of compression casting variable on concrete stress-strain curve. (a) Compression casting height,(b) compression pressure, (c) duration of compression,(d) water-cement ratio.

3 压缩浇筑混凝土应力-应变关系模型

3.1 应力-应变曲线方程

本研究采用过镇海［16］提出的混凝土受压应力-应变全曲线方程进行分析，见式（1）和式（2）.

其中，x=ε/εco，y=f/fco；ε为混凝土的应变；f为混凝土的应力；a和b为待定参数.

利用最小二乘法对试验所得数据进行拟合，得到了压缩浇筑混凝土的待定参数a和b的值，见表3.图3描述了参数a和b与抗压强度的关系，可以看出，a值随着压缩浇筑混凝土强度的增加而减小，b值随着压缩浇筑混凝土强度的增加而增大.在此基础上拟合了a、b与混凝土强度的关系式，见式（3）和式（4），a和b的相关性系数分别为0.826 4和0.730 4.

表3 压缩浇筑混凝土的参数a和bTable 3 Parameters a and b

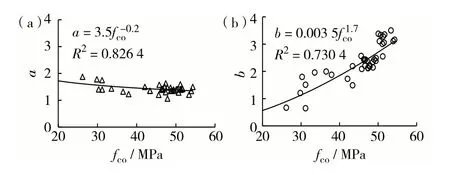
图3 参数a和b与抗压强度fco的关系 （ a）a与fco；（ b）b与fcoFig.3 Relationship between parameters a and b and compressive strength fco. (a) a vs. fco and (b) b vs. fco. Triangles and circles are the measured results and the solid line represents the fitted line.

3.2 试验与拟合曲线比较

将式（3）和式（4）计算得到的压缩浇筑混凝土应力-应变曲线待定参数a和b代入式（1）和式（2），便可得到压缩浇筑混凝土应力-应变曲线.当压缩高度为300 mm，压缩压力为15 MPa，压缩时间为2 min时，实测曲线与模型计算结果如图4所示. 从图4可以看出，不同水灰比时计算和实测的应力-应变曲线均有较好的吻合性.

图4 压缩浇筑混凝土应力-应变曲线计算值与实测值的比较 （a）水灰比为0.53； （b）水灰比为0.63； （c）水灰比为0.73； （d）水灰比为0.83Fig.4 Comparison of the calculated and measured values of the stress-strain curve of compression cast concrete when water cement ratio is (a) 0.53, (b) 0.63, (c) 0.73, and (d) 0.83. Solid lines are the measured results and the dash lines are the predicted results from the proposed model.

4 压缩浇筑混凝土构件抗弯设计等效矩形应力块参数推导

钢筋混凝土构件可以通过传统的等效矩形应力块法进行抗弯设计.如果已知以下3 个应力块参数，则可以很方便地预测出构件抗弯承载力：①极限承载力时混凝土受压区边缘纤维应变，通常也称为混凝土极限压应变εcu；② 等效矩形应力块的应力与混凝土强度的比值α1；③ 等效矩形应力块的高度与混凝土受压区高度的比值β1. 图5 显示了这3个参数的物理含义.其中，h和l分别为截面高度和宽度；d为截面有效高度；c为混凝土受压区高度；fy和Ast分别为纵向受拉钢筋的屈服强度和截面积；εst为纵向受拉钢筋的应变；F为混凝土受压区合力.应力块参数的值取决于混凝土材料特性［17］.试验结果表明，压缩浇筑混凝土应力-应变曲线不同于普通浇筑混凝土，其峰值应力后的曲线下降段较普通混凝土更陡，受压脆性更明显.因此，普通混凝土的等效矩形应力块系数不再适用于压缩浇筑混凝土，有必要提出适用于压缩浇筑混凝土构件抗弯设计所需的等效矩形应力块系数.在过去，这些参数需从受弯试验结果拟合获得［17］，但该方法成本高昂. 近年来有学者使用新提出的钢筋混凝土构件受弯定理来推导这3个等效矩形应力块参数［17-21］.本研究使用该方法得出压缩浇筑混凝土的等效矩形应力块参数.

图5 极限弯矩下钢筋混凝土截面应力和应变分布Fig.5 Strain and stress blocks at onset of flexural strength of reinforced concrete section.

4.1 受弯定理概述

WU 等［17-18］推导出了钢筋混凝土构件抗弯设计的3个数学定理，确定了钢筋混凝土截面弯矩-曲率曲线上的两个临界点（峰值弯矩点以及极限曲率点），并推导出了钢筋在峰值弯矩点前屈服（适筋）、抵达峰值弯矩点时屈服（界限状态）以及峰值弯矩点后屈服（超筋）3种不同情况下的等效矩形应力块参数的解析解，用该解析解计算出的抗弯设计的混凝土极限压应变如图6.该定理已经应用于纤维增强复合材料（fiber reinforecd polymer， FRP）筋混凝土构件、FRP筋珊瑚骨料混凝土构件、高温下钢筋混凝土构件的抗弯设计模型的推导［19-21］.考虑到规范不允许超筋构件，本研究仅给出适筋构件的等效矩形应力块参数表达式.

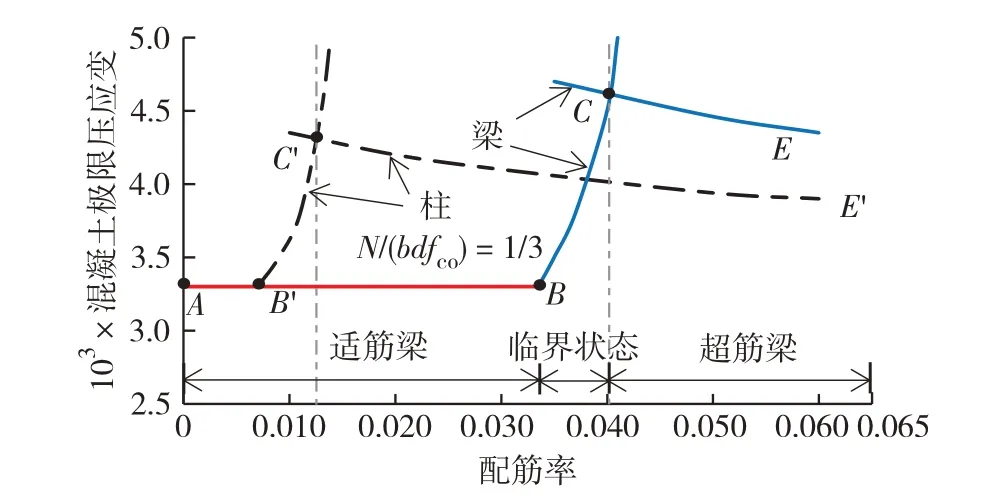
图6 抗弯设计的混凝土极限压应变Fig.6 Ultimate compression strain of concrete for flexural design.

由受弯定理可知，在适筋情况下，受弯构件的混凝土极限压应变εcu仅与混凝土的应力-应变关系有关，与配筋率无关（图6）.极限压应变εcu［17］为

其中，ε为混凝土应变；f（ε）为混凝土应力-应变关系的曲线方程.

等效矩形应力块系数α1和β1［17］为

4.2 压缩浇筑混凝土等效矩形应力块参数推导

基于本研究提出的压缩浇筑混凝土的应力-应变曲线模型，用式（5）对36个压缩浇筑混凝土的极限压应变值εcu进行了计算，结果如图7（a）所示.由图7（a）可见，压缩浇筑混凝土的极限压应变εcu与抗压强度fco呈指数正相关，因此拟合出εcu与fco的关系为

图7 抗压强度与等效矩形应力块参数的关系 （a） fco 与 εcu； （b） fco 与 α1； （c） fco 与 β1Fig.7 Relationship between compressive strength and equivalent rectangular stress block parameters. (a) fco vs. εcu, (b) fco vs. α1, (c)fco vs. β1. Circles are the calculated values and the solid line represents the fitted trendline.

式（8）与式（5）计算结果比值的均值、均方差和相关系数分别为0.959 1、0.002 4和0.997 4，表现出很高的拟合精度. 通过式（6）和（7）对压缩浇筑混凝土构件抗弯设计的等效矩形应力块参数α1和β1进行了计算，结果如图7（b）和图7（c）. 可以看出，α1和β1均与压缩浇筑混凝土抗压强度fco呈负指数相关关系，因此拟合出α1、β1与fco的关系为

式（9）与式（6）计算结果比值的均值、均方差和相关系数R2分别为0.999 7、0.000 2 和0.998 5，式（10）与式（7）计算结果比值的均值、均方差和相关系数分别为1.001 3、0.000 4和0.998 5，均表现出了很高的拟合精度. 相比于通过受弯定理（式（5）至（7））中复杂的积分运算求解压缩浇筑混凝土受弯构件的等效矩形应力块参数，本研究提出的模型（式（8）至（10））可以在充分反映等效矩形应力块参数实际值的同时，为工程应用带来了极大便利.

4.3 与各国规范模型的比较

本研究提出的等效矩形应力块参数模型与各国规范取值的比较见图8. 图8（a）为各国规范对εcu的取值，对于GB 50010—2010［22］，当混凝土强度等级小于C50 时，εcu取值为0.003 3；当混凝土强度等级大于C50 时，εcu是fco的函数，ACI 318—2019［23］的εcu取值为0.003，Eurocode2—2004［24］（混凝土强度等级小于C50）和CSA A23.3—2019［25］的εcu取值均为0.003 5. 由式（5）可知，εcu值与混凝土应力-应变关系有关，即随着混凝土强度等级的变化而变化. 本研究模型计算的混凝土极限压应变εcu值要低于各国规范取值，即用现有普通混凝土的模型会严重高估压缩浇筑混凝土极限压应变. 这主要是由于压缩浇筑混凝土的脆性造成的，经过压缩浇筑后，混凝土抗压强度和弹性模量显著提高，但峰值应力对应的应变减小、峰值应力后的应力-应变曲线下降段更陡，变形能力降低，从而造成压缩浇筑混凝土的极限压应变偏低. 混凝土极限压应变的高估将直接导致压缩浇筑混凝土构件抗弯承载力的高估. 因此，现有普通混凝土的极限压应变模型不适用于压缩浇筑混凝土构件的抗弯设计. 利用式（8）可准确计算压缩浇筑混凝土极限压应变，进而较为准确地计算压缩浇筑混凝土构件的抗弯承载力.

图8（b）为本研究提出的参数α1模型值与不同国家规范的取值对比，参数α1值大于美国规范ACI 318—2019［23］和加拿大规范CSA A23.3—2019［25］的取值，但小于中国规范GB 50010—2010［22］和欧洲规范Eurocode 2—2004［24］的取值. 这表明现有规范均无法准确计算压缩浇筑混凝土构件抗弯设计中的等效矩形应力参数α1. 基于此，当给定压缩浇筑混凝土抗压强度时，可用式（9）计算参数α1. 图8（c）为本研究提出的参数β1模型值与不同国家规范取值的对比，参数β1值与美国规范ACI 318—2019［23］、加拿大规范CSA A23.3—2019［25］取值差别较大，与中国规范GB 50010—2010［22］和欧洲规范Eurocode 2—2004［24］推荐值较为接近，但总体偏小. 这同样表明现有规范中的参数β1值均不适用于压缩浇筑混凝土. 当给定压缩浇筑混凝土抗压强度时，可用式（10）计算参数β1.

5 结 论

压缩浇筑方法可以显著提高混凝土的力学性能，应用现有混凝土应力-应变模型回归试验结果，得到适用于压缩浇筑混凝土的应力-应变关系模型，并推导得出压缩浇筑混凝土构件抗弯设计所需的等效矩形应力块参数模型，可得：

1）相比于普通浇筑混凝土，压缩浇筑混凝土抗压强度和弹性模量显著提升、峰值应力对应的应变略微减小，峰值应力点后应力-应变曲线下降更陡；

2）在现有的普通混凝土应力-应变关系模型的基础上，通过试验数据拟合得到了压缩浇筑混凝土的应力-应变关系模型；

3）利用混凝土构件抗弯设计定理计算了压缩浇筑混凝土构件抗弯设计所需的等效矩形应力块参数，并得到了与压缩浇筑混凝土强度相关的简化模型，其中，εcu与混凝土强度呈指数正相关关系，α1和β1与混凝土强度呈指数负相关关系；

4）现有规范模型均无法准确预测压缩浇筑混凝土构件的等效矩形应力块参数，用现有混凝土规范进行压缩浇筑混凝土构件的抗弯设计会造成较大的误差. 可利用本研究所提出的模型对压缩浇筑混凝土构件进行抗弯设计.