一种停车场最优停车路径规划设计

毛国龙 MAO Guo-long；张亚秋 ZHANG Ya-qiu；赵海茹 ZHAO Hai-ru

（玉溪师范学院，玉溪 653100）

0 引言

到2022 年年末，公安部交通局的统计结果显示，中国的车辆总量已经超过4.17 亿辆，其中汽车数量为3.19 亿辆，占到了76.59%。人们在享受车辆出行便利的同时，也不得不面对一个日益严重的问题——停车难。由于我国城市土地资源十分宝贵，停车场建设面临土地成本与资金成本过高问题。汽车增长量与停车场增长量难以匹配，在车流高峰期面临无车位可停，因此，从满足用户需求车位和路径引导两方面去解决停车难问题迫在眉睫。

为改善这一状况，国内外学者针对城市道路导航、停车位利用率及停车场内路径规划进行了大量研究。德国A.Sanaa 教授利用蚂蚁群算法，研究了当地车流和停车场的拥挤情况，设计出一套停车诱导屏安装在城市的多处重点路段，显示当地的车流情况以及车位的实际情况，为市民提供了一种有效的出入管理服务[1]。E.Jonkers 教授和他的同事们深入探讨了三种不同的停车位以及它们的使用困难程度，最终构建出一个完整的停车场路线引导系统[2]。关志宏教授和他的团队将停车区域细化，并利用模拟技术将停车场区域分解来实现自动化管理。随着导航技术的快速发展，对停车难这一问题的研究更多集中到停车场的智能化管理方向，主要就停车位的利用率和智能化管理两个方面开展研究。

截止目前，停车场路径引导面临以下两个挑战：第一，大型复杂的地下停车场怎样建模在研究最短路径算法中起着比较重要的作用，如何构建出更为精细的、更具代表性的地下停车场模型，以便更好地实现最优的路线规划；第二，停车场内的道路网络密集，采用传统Dijkstra 算法来实现路线规划将面临更高的计算负担，如何改善算法以提高算法的效率和精度。

本文以既定停车场为对象，分别以距离停车场出口最近、距离电梯口最近为目标，对停车场进行路径规划研究。

1 最短路径规划

1.1 车主泊车行为分析

当车主首次进入停车场时，由于对停车场内地形的不熟悉，此时车主只能通过反复巡航和个人偏好来快速寻找停车位，寻找到的停车位也不一定是当下情况的最优停车位。此外，停车位的形状、周围障碍物分布、停车场内道路分布、距离电梯口的距离和距离出口的距离等将会影响着车主的选择。

1.2 路径规划算法

1.2.1 Dijkstra 算法

Dijkstra 算法是荷兰的一位计算机专家狄克斯特拉在1959 年提出的一种方法，该算法解决的是有权图中最短路径问题。Dijkstra 算法的主要特征是：从起始点出发，采用贪婪算法的策略，每次遍历到距离起始点最近且未访问过的顶点的邻接节点就将其扩展进来，直至包含图中所有的节点[3]。

Dijkstra 算法的思路：把有权图的全部节点分成集合P 和Q，起始点为S，P 记录已求得的最短路径的节点（SP）；其余节点包含于集合Q 中；集合P 每并入一个新顶点，都要修改起始点S 到集合P 中各节点当前的最短距离和最短路径。算法实现需要两个辅助数组：dist[]用来保存起始点到其余各顶点当前的最短距离；path[]用来保存起始点到其余各顶点的最短路径，path[i]表示起始点到顶点i之间的最短路径的前驱节点，算法结束时，可以根据其值追溯到起始点到节点i 的最短路径。假设从起始点S 出发，邻接矩阵Edge 代表无向带权图，Edge[i，j]代表节点i与节点j 的无向边权值，若两节点不邻接，值为∞。

过程如下：①初始化：集合P 初始化为{S}，dist[]的初始值dist[i]=Edge[S，i]，path[]的初始值path[i]=[i]；②从集合Q 中选出节点j，满足dist[j]=min{dist[i]}，令P=P∪j；③修改从S 出发到集合Q 中任一顶点k 可达的路径最短长度，即若dist[j]+Edge[j，k]＜dist[k]，则更新dist[k]=dist[j]+Edge[j，k]；④重复②～③，直到所有的顶点都包含在P 中。

以图1 停车位模型为例子进行简单的说明，假设车辆从入口进入，需要前往4 车位。根据表1，入口到4 车位的最短距离为5，最短路径为入口-1 车位-4 车位。

表1 图1 模型入口至各车位最短路径寻找过程

图1 停车位模型

1.2.2 A*算法

A*算法是一种路径搜索算法，于1968 年由P.E.Halt、NJ.Nilsson 和B.RaPhacl 等学者提出。A*算法是一种启发式算法，它是基于深度优先算法（以最快速度找到连接起始点与目标点的路径，但路径不一定最优）和广度优先算法（确保路径最优，但需遍历所有节点，复杂度高）的一种融合算法，它基于启发函数构建代价函数，既考虑了新节点距离起始点的代价，又考虑了新节点与目标点距离的代价。A*算法的代价函数表示为：

式中，f（n）是由起始节点经由节点n 到目标节点的代价估计，g（n）是由初始节点到节点n 的实际代价，h（n）是从节点n 到目标节点的最佳路径的估计代价（启发函数）。A*算法在搜索过程中，通过代价函数对当前节点与目标节点之间的距离进行估计，以此来判断节点是否处于最优路径，并优先搜索最近的节点，从而高效地找到目标节点，减少不必要的节点搜索，提高搜索效率[4]。

1.2.3 Foyd 算法

Foyd 算法，是1962 年由美国数学家Floyd 发明的，它旨在找到无向图中任意两个节点之间的最短路线，它的基本思想就是利用Dijkstra 算法的多次迭代，对每个节点的中间路径进行搜索，并且根据搜索的结果，找到权重最低的那条路径。与Dijkstra 算法相比较，Dijkstra 算法用于计算图中起始点到其他顶点的最小距离；Foyd 算法中，每一个顶点都是起始点，所以要将每一个顶点视为目标顶点，计算任意两个顶点之间的最小距离。

这种方法的好处在于，能够快速地确定两点之间的最小距离，而且程序的编程也相对简便，然而，其缺点在于耗费的时间相对较长，尤其在处理大规模的停车场上，不适合计算大量数据[5]。

2 基于Dijkstra 算法的停车场最短路径规划

2.1 停车场模型设计

在进行停车场路径规划时，首先要把停车场内部的路径和停车位信息进行定义，省略其他次要信息，只保留停车位和路径信息以及距离进行数据建模。

根据本次模拟的数据，将其通过MATLAB 建立简单的平面模拟图，省略了停车场的外部围墙、立柱、相对位置等信息，只保留了停车场内的道路、停车位和各个路段的距离等三项关键信息。模拟图内1 为入口，如图2 所示。

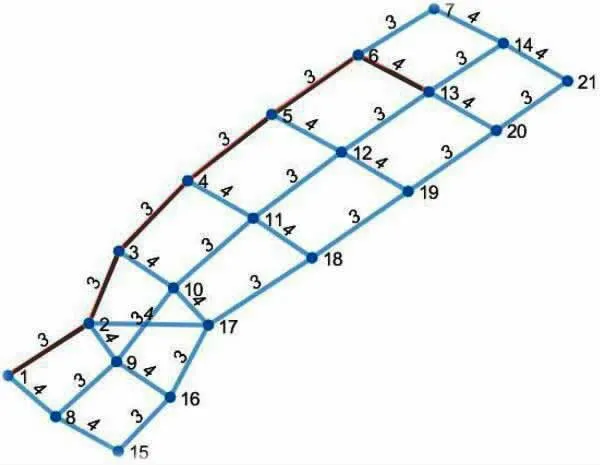
图2 停车场车位平面模拟图

2.2 基于Dijkstra 算法的最短路径规划

课题以停车场入口为起始点，以距离出口最近的目标车位为终点进行最优路径规划。在上述停车场平面数据模型基础上，把最优路径规划问题转换成了停车场内位置距离无向权图最短路径问题，也就是利用Dijkstra 算法，在平面模拟停车场无向带权图中研究停车场最短路径问题，路径通过的各节点的权重之和最小为最佳路线。其算法流程如图3 所示。

图3 算法实现过程示意图

本次实验均在MATLAB 下进行仿真，在仿真实验中，经典Dijkstra 算法通过选用邻接表的方式进行计算，避免了需要存储大量的计算数据的缺点。Dijkstra 算法本身的时间复杂度为N2，因此在后期增加停车场车位数量时计算时间明显增加，且出现了计算出错、计算结果不正确等情况。

当车位数量较少时，算法输出稳定，可准确规划出入口至各车位的最短路径。图2 停车场模型最短路径规划结果如表2 所示。以图2 黑色标识的路径为例，入口为1，出口为13 时，最优路径为1-2-3-4-5-6-13，在该路径上，距离出口（13 节点）最近的节点即为最佳推荐车位，入口距出口的最小距离为19。

表2 图2 停车场模型规划出的最短路径及最小距离

3 改进的基于Dijkstra 算法最短路径规划

实际生活中，当车主进入到一个陌生停车场寻找车位时，离电梯口或人行出入口更近、步行距离更短往往是比距离出口较近更为迫切的需求。因此，课题在以上最短路径规划的基础上进行改进，增加电梯这一考量目标，以距离电梯最近为目标进行路径规划。为便于比较，停车场采用数据量更小的数据模型2 进行仿真分析，如图4 所示。

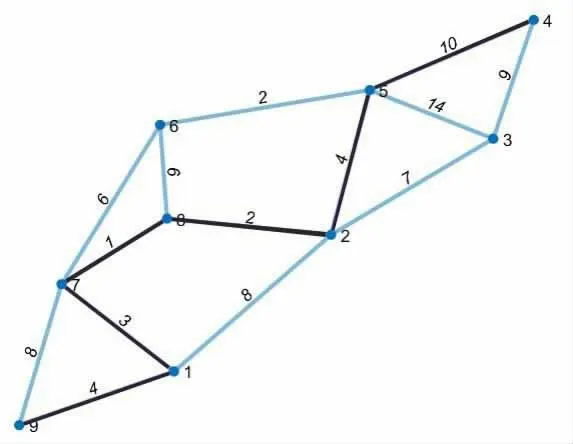
图4 停车场车位数据模型2

结合实际停车情况，入口、出口和电梯所在节点不作为车位，其余节点均视为空闲可用车位，并增加如下限制条件：第一，路径上必须包含停车位，避免车辆直接由入口到出口不停车；第二，为突出步行距离（即停车位距电梯口的距离）越短越好，将步行往返距离权重乘2 计入总和距离，即总和距离=最优路径长度+步行距离*2（往返）*2（加权），改进后的最优路径及最佳车位推荐以总和距离最小为最优。为了验证和对比改进前和改进后最短路径规划的有效性，本实验将改进前和改进后的实验数据进行对比，如表3 所示。表中，改进后的最优路径灰色字体的前一个节点为最佳车位。从表3 数据可以看出，改进前规划的路径车辆行驶路径最短，但如果考虑到步行代价较车辆行驶代价更高，即改进后的算法以车辆及步行总和距离最小为目标进行路径规划，规划出的路径较改进前总和距离明显减小，验证了改进后的Dijkstra 算法的有效性。能够有效地减少用户在泊车过程中的盲目巡航所造成的浪费。

表3 图4 所示停车场数据模型改进前后路径规划对比

4 总结

本文所研究的基于Dijkstra 算法的最优路径规划能够给出最短路径、推荐最佳车位；在考虑步行距离时，改进的Dijkstra 算法能够推荐总和距离最近的路径及对应的停车位。同时，可以依据不同停车场实际情况更改停车场模型数据，对当下智能停车引导系统方面的研究具有一定的补充意义，尤其是在室内停车引导系统方面有一定的借鉴作用。