景区应急疏散的动态路线规划算法研究

胡明明 李新娥 杨丽梅，*

（1.广西大学工商管理学院，广西南宁 530004；2.广西大学经济学院，广西南宁 530004）

0 引言

近年来，旅游业高速发展，旅游规模和体量大跨步向前，国民在假期集中出游意愿较为强烈，“拥堵”成了假期旅游的常态，游客滞留也频繁发生。在拥堵的状态下，高密度人群处于高度恐慌和兴奋状态，极易发生踩踏和社会治安事件，给人员安全疏散带来极大的困难和挑战，也大大增加了景区处理火灾、洪水、泥石流、山体滑坡等突发公共事件的难度，景区应提前科学安排人群应急疏散计划。当前景区多采用静态应急疏散路线规划方案，游客短时间内的同向运动极易导致道路和汇聚点拥堵，疏散效率较低。因此，如何科学规划应急疏散线路，安全快速地疏散游客，尽可能减少由灾害导致的人员伤亡和财产损失，已成为景区应急管理中亟须解决的问题，也吸引了诸多国内外研究者的关注。

随着计算机技术的不断发展，计算能力的不断提升，计算机仿真已成为人群应急疏散研究的重要手段（胡玉玲 等，2014）。常见的人群应急疏散仿真模型可以分为宏观模型和微观模型（Weng et al.，2007）。宏观模型将人群视为一个整体，通过借鉴其他学科的理论和方法来研究行人群体的行为特征（廖灿 等，2020），如研究者常用流体动力学（Bretschneider et al.，2011）、蚁群算法（Sun et al.，2020；王润泽等，2020）等方法来探究人群应急疏散路径的优化问题（苗志宏 等，2014）。微观模型则从行人的角度，分析在动态环境中的个体行为对行人流整体的影响，常用的微观模型包括元胞自动机模型（Tang et al.，2015；姜兰 等，2019；宋英华 等，2020）、社会力模型（钟圳伟 等，2020；Helbing et al.，1995；Han et al.，2017）、多智能体模型（Beltaief et al.，2011；Fadhli et al.，2020）、相互速度障碍模型（Van Berg et al.，2008；黄鹏 等，2012）、FIRECAMTM模型（Surawski et al.，2012）等。宏观模型以人群整体为建模对象来研究群体运动规律，忽略了个体间的相互作用和差异（胡玉玲 等，2014），微观模型则考虑了个体间的特征与差异，以及环境对个体生理、心理（Bryan，1957）的影响，对疏散者行为的描述更接近于现实（苗志宏 等，2014）。

根据路网信息在疏散中是否发生变化，人员疏散中的路网环境信息可分为静态和动态两类（周敏 等，2019）。其中，静态环境信息包括出口的位置和宽度、障碍物的位置、疏散标志、道路疏散能力、路径长度等不随时间变化的信息。动态信息包括危险源的蔓延速度、道路拥堵状况、出口拥挤程度等随时间变化的信息（韩延彬，2019）。静态疏散路线规划不随动态环境的变化而改变，而动态疏散路线规划考虑了动态环境信息，疏散路线实时调整和优化，能有效缩短疏散时间，吸引了诸多国内外研究者的关注。例如：王润泽等（2020）通过实证研究发现在疏散线路规划中实时考虑交通拥堵路况信息，能有效降低车辆平均疏散时间和总疏散时间。Khalid 等（2018）采用人工免疫系统算法证明了动态环境信息对疏散计划的效率有直接影响。Pourrahmani 等（2015）基于模糊可信度理论的遗传算法动态调整公共车辆的疏散线路，优化了城市公共交通的疏散路线方案。Liu等（2019）运用经典的Floyd-Warshall 算法模拟真实的交通网络，证明了实时计算每对节点之间的最短路径并及时优化调整出行线路能大大减少车辆行驶时间，比非实时计算减少45%以上。Liebig 等（2017）基于未来交通风险预测和最新交通状态数据，提出个人出行路线规划系统。研究发现，疏散人员的社会关系也会影响疏散线路的选择（Wang et al.，2009），如组团出行的家人、朋友和同事等一般会选择相同的疏散路线，因此动态应急疏散路线规划还应考虑组团人员群体凝聚力的影响（Khalid et al.，2018）。

人员伤亡概率与其处于灾害区域的时间成正比，因此在最短时间内将受灾人员疏散至安全区域是应急疏散的首要目标，总疏散时间（Qing et al.，2022；Fadhli et al.，2020；Patel et al.，2016）和疏散路径长度（Sun et al.，2020；Stepanov et al.，2009；Patel et al.，2016）是应急疏散效率的重要评价标准。而疏散时间受到道路长度（Patel et al.，2016）、宽度、坡度（Aghabayk et al.，2021）、人群密度（Nelson et al.，2002；Fruin，1971；李俊梅 等，2014）等的影响，还受出口宽度（Huang et al.，2008）、道路通行能力、安全疏散时间等的约束。1978 年，Predtechenskii 等（1978）首次探讨了行人速度和人群密度之间的关系，发现行人速度与人群密度成反比。Nelson等（2002）进一步探讨了在不同疏散通道中（楼梯、过道、走廊等）行人速度与人群密度的关系，并得出与前人一致的结论。Aghabayk 等（2021）探讨了坡度对行人速度的影响，发现上坡时行人速度随坡度增大而减小，下坡时则随坡度的增大先增大后减小。研究表明，当行人对疏散环境不熟悉时会倾向于采取“就近原则”，即选择距离其最近的出口作为其疏散出口，将最短距离路线作为其疏散路线（Kuang et al.，2009）。综上所述，时间或空间维度上的最短路径，即最短疏散时间路线或最短疏散距离路线将作为行人的应急疏散路线。

经典的最短路径算法如Dijkstra算法（李梦雅 等，2016）和Floyd算法（张蓉 等，2016）常被用来研究应急疏散路线规划问题。Dijkstra 算法为E.W.Dijkstra 于1959年提出的典型单源最短路径算法，采用遍历搜索方式求解最短路径（任伟建 等，2018），具有规划路径用时短、更新路径动作快（金云 等，2022）、可靠性高、鲁棒性好（曹祥红 等，2020）的优点。李梦雅等（2016）以总疏散时间最短为目标，对Dijkstra 算法进行改进，构建洪灾避难应急疏散路径规划模型，有效减少了疏散时间和人员伤亡。针对多数建筑综合体单一疏散路线缺乏灵便临场应急处理能力的问题，张蓉等（2016）提出最优路径、动态调整、即时反馈的新思路，基于Floyd 算法建立实时应急疏散路线发布平台，实现了应急疏散路径实时动态的智能规划。

虽然国内外研究者在人群疏散仿真模型构建、疏散路径动态规划和疏散效率评价等方面取得了一定的研究成果，但仍存在以下问题：

（1）现有的行人应急疏散路径动态规划多以建筑物内动态疏散为主，建筑物外的动态疏散相关研究较少，尚未有研究者对景区内行人的动态疏散路径规划展开研究。而出于环境保护和避免拥堵等方面的考虑，旅游景区常常限制外来车辆出入，且景区内多狭小、弯曲的步行道，内部观光车辆无法通达，景区内部交通仍以行人步行为主。因此，对景区内行人的动态应急疏散研究意义重大。

（2）现有研究中同时考虑道路的长度、宽度、坡度、人群密度等因素对应急疏散路线规划影响的较为少见，这些变量常常被设定为一个特定的常数，这与现实情况不太相符。

因此，本文在现有研究的基础上提出一种基于Dijkstra算法的景区行人动态最短时间应急疏散路线规划（DSTEERP）算法，该算法同时考虑了道路的长度、宽度、坡度、实时人群密度等因素对行人疏散效率的影响，并以总疏散时间作为效率评价标准，探讨景区采用动态疏散路线规划算法的效率。

1 模型假设与参数设定

本文提出的基于Dijkstra 算法的DSTEERP 算法采用遍历搜索方式求解最短应急疏散路径，即以起始节点为中心向外层层拓展，直到遍历所有节点，拓展到终点为止，最终选择疏散时间最短的路线作为其当前时刻的最佳应急疏散路线。同时考虑到路网状况实时变化，每间隔一段时间更新路网数据，并重复遍历搜索所有节点，得到新一时刻的最佳应急疏散路线，直至路网中应急疏散行人数量等于0为止。

1.1 模型假设与符号说明

本文对应急疏散模型做出以下假设：

（1）将弯曲道路近似看作直线；

（2）同一道路上宽度、坡度、人群密度和疏散速度相同；

（3）路网中全部行人同时疏散，且相同位置行人有相同应急疏散路线选择；

（4）应急疏散路线根据实时路网数据求解，且所有行人按照给定疏散路线进行疏散。

为了构建景区应急疏散路线动态优化算法的数学模型，本研究涉及的参数如表1所示。

表1 模型参数

1.2 算法参数设定

（1）人群密度

路网中矢量道路eij上的人群密度用ρij表示，道路上的人群密度值等于该道路上的行人总数与该道路面积之比，其中，道路面积为其长度与宽度的乘积。因此，ρij的计算公式如下所示：

式（1）中，mij、lij和wij分别代表矢量道路eij上的行人总数、矢量道路eij的长度和宽度。

（2）道路坡度

根据《国家森林公园设计规范》（GB/T 51046—2014），森林公园类旅游景区内部的主干道路纵坡小于等于9%，支路纵坡小于等于13%，因此，本文假设景区内道路的坡度范围为-0.13 到0.13（负数和正数分别表示下坡路和上坡路）。本文将弯曲道路近似看作直线，并根据道路长度、道路起止节点的海拔差近似计算该道路的坡度（坡度值为矢量值）。计算公式如下所示：

式（2）中，sij表示矢量道路eij的坡度，lij为矢量道路eij的长度，hdij为起始节点i与终止节点j海拔高度差。

（3）行人疏散速度

行人疏散速度与道路的坡度、人群密度相关。本文结合Aghabayk 等（2021）的研究成果，采用三阶多项式（陈岚峰 等，2014）拟合应急疏散中的行人速度与坡度之间的关系曲线，得到矢量道路eij上考虑了坡度的行人疏散速度vsij（单位：m/s）的拟合函数如下所示：

根据Nelson 等（2002）的研究结果，行人疏散速度v=1-0.266×k×ρ(0.54 人/m2≤ρ≤3.8 人/m2)，其中k为常数（k值由疏散通道类型决定），行人的疏散速度和人群密度呈负线性关系（见图1）。

综上，对行人疏散速度、道路坡度、人群密度的关系函数做规范化处理，得到行人疏散速度（单位：m/s）函数如下所示：

根据行人疏散速度与坡度的拟合结果，绘制不同坡度（-0.12，-0.06，0.00，0.06，0.12）道路上行人速度与密度的关系图，如图1右图所示，当人群密度为0.54人/m2～3.8人/m2时，速度随人群密度增加而减小；当人群密度小于0.54人/m2时，速度不受人群密度影响。

（4）时间距离

疏散路网中矢量道路eij的时间距离用tij表示，即行人从该道路的起始节点疏散至终止节点所需的时间，计算公式如下：

式（5）中，lij表示矢量道路eij的长度，当其值为无穷大时，表示节点i到节点j无可通路径；vij表示行人在矢量道路eij上疏散的速度。

（5）个体线路选择方案

行人遍布路网各处，不同位置的行人有不同的路线选择方案，且行人在路口和路段中的疏散路线求解方法不同。当行人位于路口即节点上时，其最佳应急疏散路线为该节点的最短疏散时间路径；当行人位于路段上时，则需比较该道路前后两个方向的应急疏散路线的疏散时间，即比较行人从当前位置分别疏散至前后两个节点，再从这两个节点疏散至安全节点的总时间，最终选择疏散时间最小的路线作为行人的应急疏散路线。

（6）疏散时间

本文采用的Dijkstra 算法中每条道路的权重为行人从该道路起始节点疏散至终止节点所需的时间，即其权重矩阵为路网的时间距离矩阵，基于此对当前时刻最短疏散时间路线进行求解。每间隔一段时间更新路网数据，并重新求解新一时刻最短疏散时间路线。最终累计各疏散行人从其初始位置撤离至安全出口的疏散时间即为该行人的疏散时间。第k个行人的疏散时间用Tk(k=1，2，…，MP)表示，MP为疏散行人总数，对所有行人的疏散时间求最大值即为该疏散活动的总疏散时间T，公式如下：

2 动态应急疏散路线规划算法

本文将景区中的道路视为边，路口视为节点，构建旅游景区拓扑结构图，则可将旅游景区内游客应急疏散路线规划问题转化为求解路网中每对节点之间的最短路径问题。经典的Dijkstra算法可以结合边的权重，对图中一个节点到任意节点的最短路径进行求解，得到最短路径的最优解。因此，本文提出了一种基于Dijkstra算法的景区行人DSTEERP 算法，求解疏散行人的最优应急疏散路线选择方案。图2为景区行人DSTEERP算法的流程图。DSTEERP算法求解步骤如下：

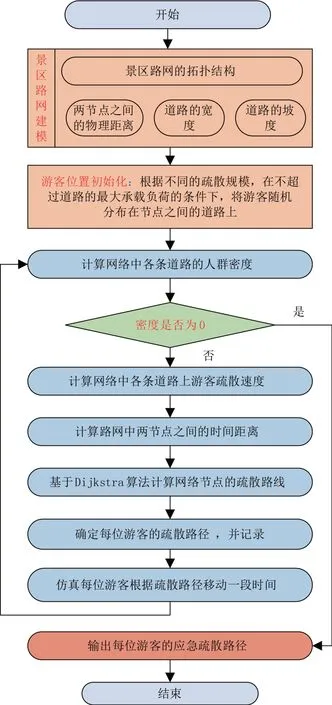
图2 动态最短时间应急疏散路线规划算法流程图

步骤1：路网数据收集和初始化

（1）收集路网数据并构建路网数据邻接矩阵。收集路网中道路的长度、宽度和各节点海拔高度数据，并构建路网中道路的长度、宽度和坡度邻接矩阵，其中，道路坡度通过公式（2）近似计算。

（2）疏散行人位置初始化。按一定人群规模以随机分布的形式确定行人的初始位置，每条道路人群密度不超过3.8人/m2（超过该范围时道路过于拥挤，行人无法向前疏散）。

步骤2：计算疏散时间矩阵

（1）计算路网人群密度矩阵。根据公式（1）计算路网中每条道路的人群密度，并构建人群密度邻接矩阵。若某一道路的人群密度为0，则表示该道路上无疏散行人，若人群密度邻接矩阵的值全部为0，则结束疏散并输出疏散结果，否则继续后续步骤。输出内容包括累计疏散路线长度、累计疏散时间和最终抵达的安全出口等。

（2）计算疏散速度和疏散时间矩阵。根据路网中道路的坡度和人群密度计算行人的疏散速度矩阵，再基于得到的疏散速度矩阵和道路长度计算行人疏散时间矩阵。

步骤3：应急疏散路线搜索

（1）位于网络节点上的行人应急疏散路线。将路网疏散时间矩阵作为权重矩阵，采用Dijkstra算法求解网络节点的最短时间路径作为其最佳应急疏散路线。

（2）位于道路路段上的行人应急疏散路线。将路网疏散时间矩阵作为权重矩阵，采用Dijkstra 算法求解道路路段前后两个节点的最短时间路径，比较疏散行人从其当前位置往前后两个不同方向进行疏散的最短时间路径的疏散时间，选择疏散时间最少的路线作为其在该时刻的最佳应急疏散路线。

步骤4：更新实时路网

按照DSTEERP 算法得到的最优应急疏散路线选择方案疏散路网中的所有行人。同时考虑到路网状况实时变化，每间隔一段时间更新路网数据，并转至步骤2。

3 算法仿真实验

为验证DSTEERP 算法能否提升应急疏散效率，本文选取静态最短时间（邢鲁宁 等，2022）应急疏散路线规划（SSTEERP）和静态最短距离（Su et al.，2008；苏兵等，2008）应急疏散路线规划（SSDEERP）作为基础模型，将二者的仿真结果与DSTEERP 进行比较。SSTEERP、SSDEERP 与DSTEERP 三种疏散模型的初始路网和假设条件是一致的，区别在于：SSTEERP 和DSTEERP 均以总疏散时间最小化为目标，但SSTEERP 不考虑实时路网情况，仅根据初始路网状态下的路网疏散时间距离矩阵求解应急疏散路线规划，而DSTEERP是基于实时路网数据动态调整游客的应急疏散路线选择方案，SSDEERP 则是以总疏散长度最小化为目标，基于路网道路长度距离矩阵求解应急疏散路线规划。

考虑到青秀山风景区和广西大学内部路网同样错综复杂，但前者路网多起伏曲折，道路网密度较小，后者路网则较为平坦笔直，道路网密度较大，故选取这两个区域作为仿真区域，运用MATLAB软件进行仿真疏散，根据DSTEERP、SSTEERP和SSDEERP 算法分别求解不同人群规模的行人应急疏散路线选择方案。为降低随机因素对疏散仿真的干扰，并探讨不同人群规模和人群密度下的疏散效率，本文对这两个仿真区域按5级人群规模分别进行5次仿真疏散，取每层级5次仿真疏散结果的平均值作为该层级的最终结果，并比较DSTEERP、SSTEERP 和SSDEERP 的总疏散时间和人均疏散时间。

3.1 青秀山风景区仿真实验

青秀山风景区位于广西壮族自治区南宁市，面积13.54 平方千米，年接待游客超500 万人次①南宁青秀山风景名胜旅游区管委会.青秀山风景区主要旅游景点介绍［EB/OL］.（2023-03-30）［2023-09-18］.http：//qsgw.nanning.gov.cn/jqfw/jdjs/t572408.html.，是南宁市唯一的国家5A 级旅游景区。青秀山风景区节假日人流密集，且路网和地形较为复杂，紧急突发情况下疏散不当极易发生踩踏事故，造成人员伤亡，因此科学制定行人应急疏散路线规划意义重大。本文运用ArcGIS 采集路网中所有节点的海拔和道路的长度、宽度等指标，并绘制路网拓扑结构图（见图3）。根据绘制的路网拓扑结构图，本实验中青秀山面积为5.74 平方千米，道路总长度为41.44千米，路网密度为7.22千米/平方千米，共167条道路120个路口（部分道路为断头路），其中115 个路口为风景区内部道路节点，用红色圆点标注，5 个为风景区出入口，用绿色五角星标注。

图3 青秀山风景区路网拓扑结构

以青秀山风景区承载量（25万人②中国政府网.旅游局发布5A 级旅游景区最大承载量并答记者［EB/OL］.（2015-07-17）［2023-09-18］.https：//www.gov.cn/xinwen/2015-07/17/content_2898961.htm.）作为仿真疏散模型的全天在园人数，则上午、下午和晚上三个时间段平均在园人数为84000人，上下浮动20000人，每个时间段景区在园人数为64000～104000人。因此，青秀山风景区设置的5级人群规模为6万人、7 万人、8 万人、9 万人和10 万人。青秀山风景区在DSTEERP 算法、SSTEERP 算法、SSDEERP算法下的总疏散时间和人均疏散时间如表2和表3所示。

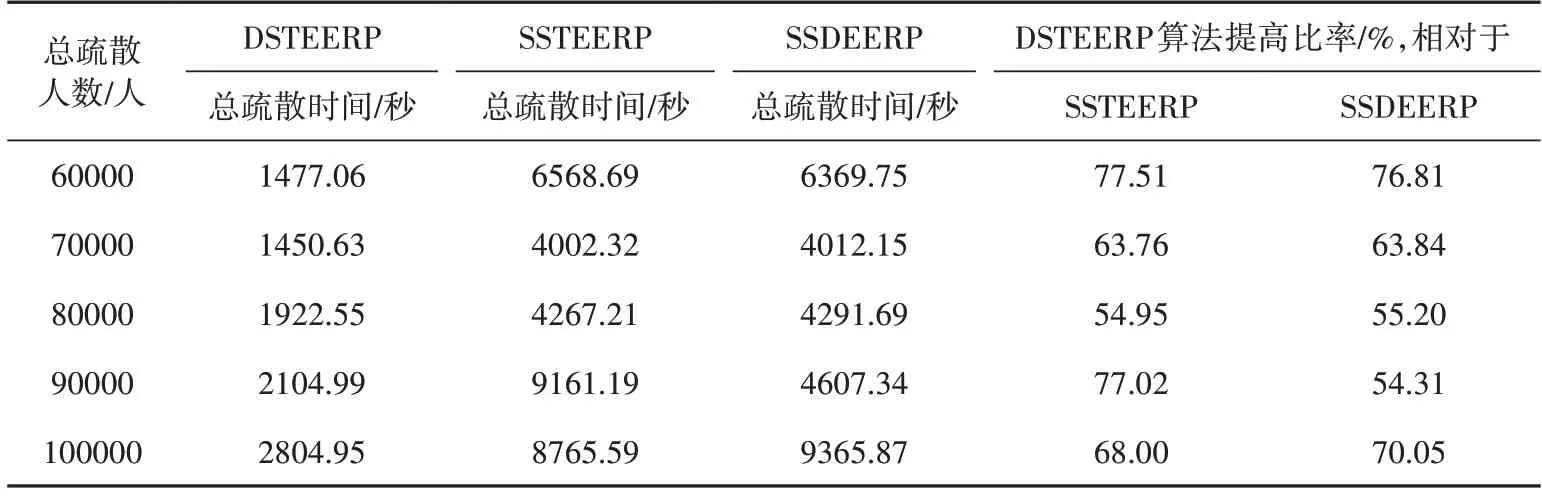
表2 青秀山风景区总疏散时间结果比较

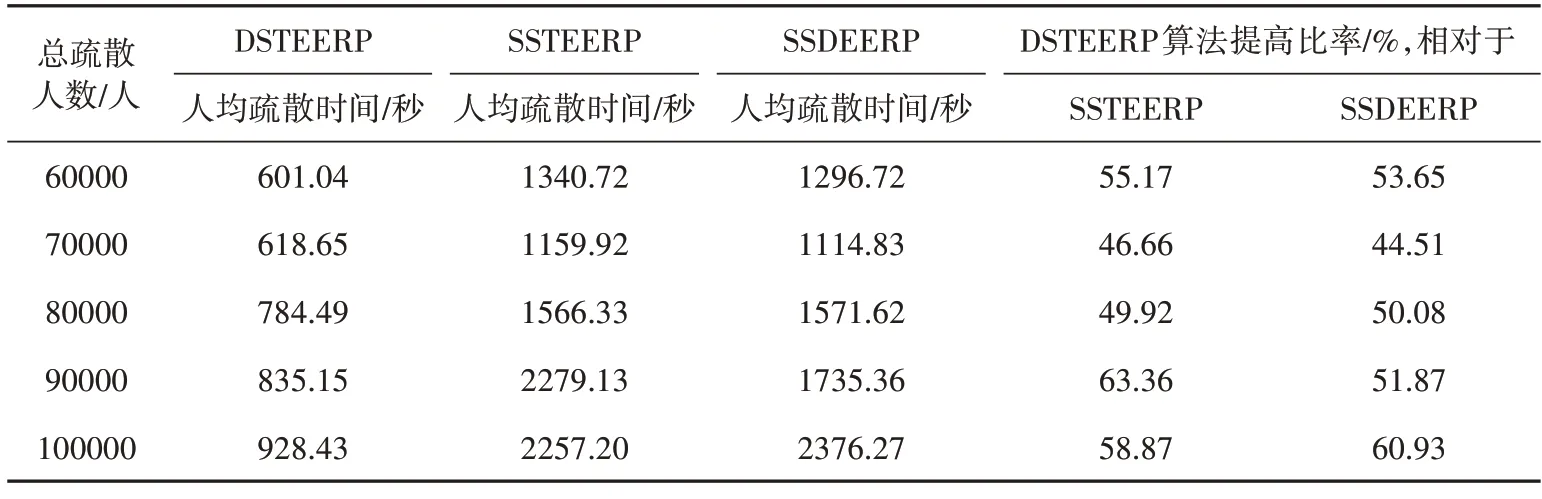
表3 青秀山风景区人均疏散时间结果比较

根据青秀山风景区行人应急疏散仿真结果，本文提出的DSTEERP算法显著地提高了疏散效率。其中，当人群规模为10万人时，DSTEERP算法、SSTEERP算法、SSDEERP算法的总疏散时间分别为0.779小时、2.435小时、2.602小时，人均疏散时间分别为0.258小时、0.627小时、0.660小时。总体来说，DSTEERP算法的总疏散时间比SSTEERP算法减少54.95%以上，人均疏散时间减少46.66%以上；DSTEERP算法的总疏散时间比SSDEERP算法减少54.31%以上，人均疏散时间减少44.51%以上。即动态应急疏散路线规划算法与两个静态应急疏散路线规划算法相比，总疏散时间和人均疏散时间均减少40.00%以上。DSTEERP算法的总疏散时间和人均疏散时间随着人群规模增大而增大，增幅较小，且均远低于SSTEERP和SSDEERP算法下的总疏散时间和人均疏散时间，说明DSTEERP算法具有更好的稳定性和优越性。

3.2 广西大学西校区仿真实验

广西大学位于广西壮族自治区南宁市，是广西唯一一所国家“211 工程”高校，占地面积约14.27 平方千米①广西大学.广西大学概况（数据截至2022 年12 月31 日）［EB/OL］.（2022-12-31）［2023-09-18］.https：//www.gxu.edu.cn/xdgl1/xxgk1.htm.。学校以崇左桥为界分为东西两个校区，其中东校区拥有大面积的农林实验基地，人群密度较小，而西校区内教学楼、办公楼和宿舍楼布局较为集中，人群密度大。因此选择西校区作为仿真疏散区域能更好地模拟紧急情况中的行人疏散情形，且有利于改善西校区的应急规划管理。本文运用ArcGIS 软件采集路网中所有道路的长度、宽度等数据，并绘制路网拓扑结构图（见图4）。根据绘制的路网拓扑结构图，本实验中广西大学西校区占地面积为1.02 平方千米，道路总长度为18.29 千米，路网密度为17.93 千米/平方千米，路网中共有197个节点和291条道路，其中190个内部节点用红色圆点标注，7个安全出口用绿色五角星标注（安全出口为校门或安全通道）。校园内大多为平直道路，故将校园内道路的坡度设为0，无需采集路网节点的海拔。

广西大学内学生、教职工及家属等常住人口近10 万人，平均每个校区常住人口约5万人②广西大学.广西大学概况（数据截至2022 年12 月31 日）［EB/OL］.（2022-12-31）［2023-09-18］.https：//www.gxu.edu.cn/xdgl1/xxgk1.htm.，在做仿真疏散时可以设最大人群规模为6万人，最小人群规模为2万人，因此，广西大学西校区设置的5 级人群规模为2 万人、3 万人、4 万人、5 万人和6万人。广西大学西校区在DSTEERP 算法、SSTEERP 算法、SSDEERP 算法下的总疏散时间和人均疏散时间如表4和表5所示。

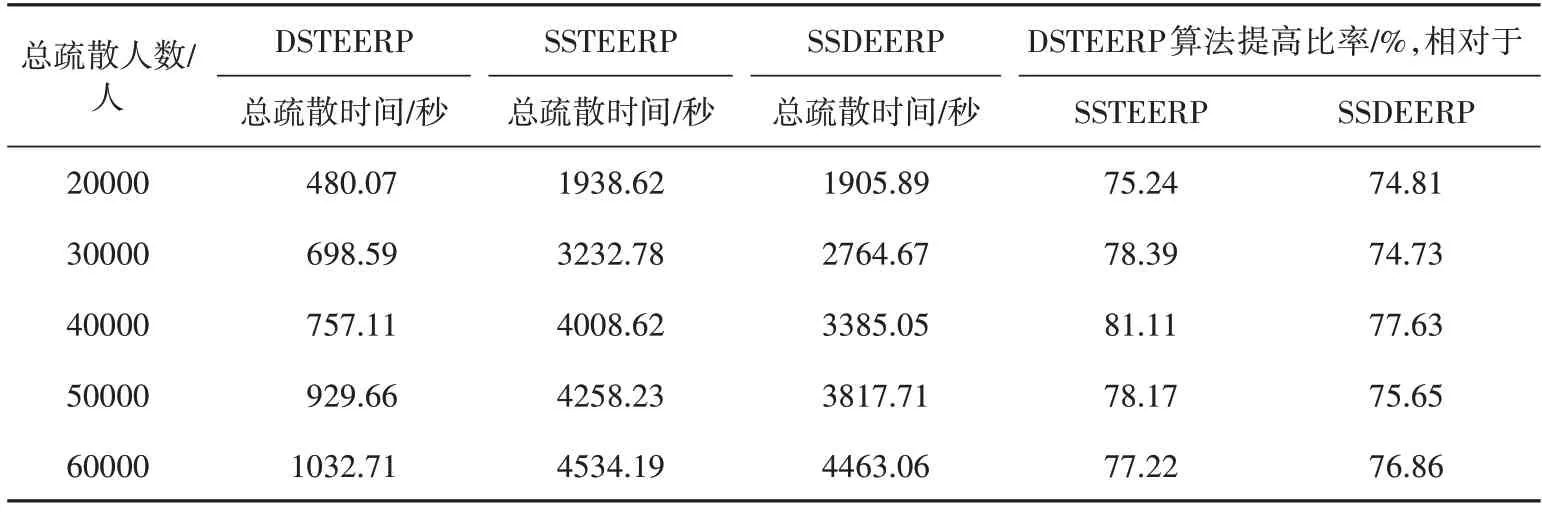
表4 广西大学西校区总疏散时间结果比较

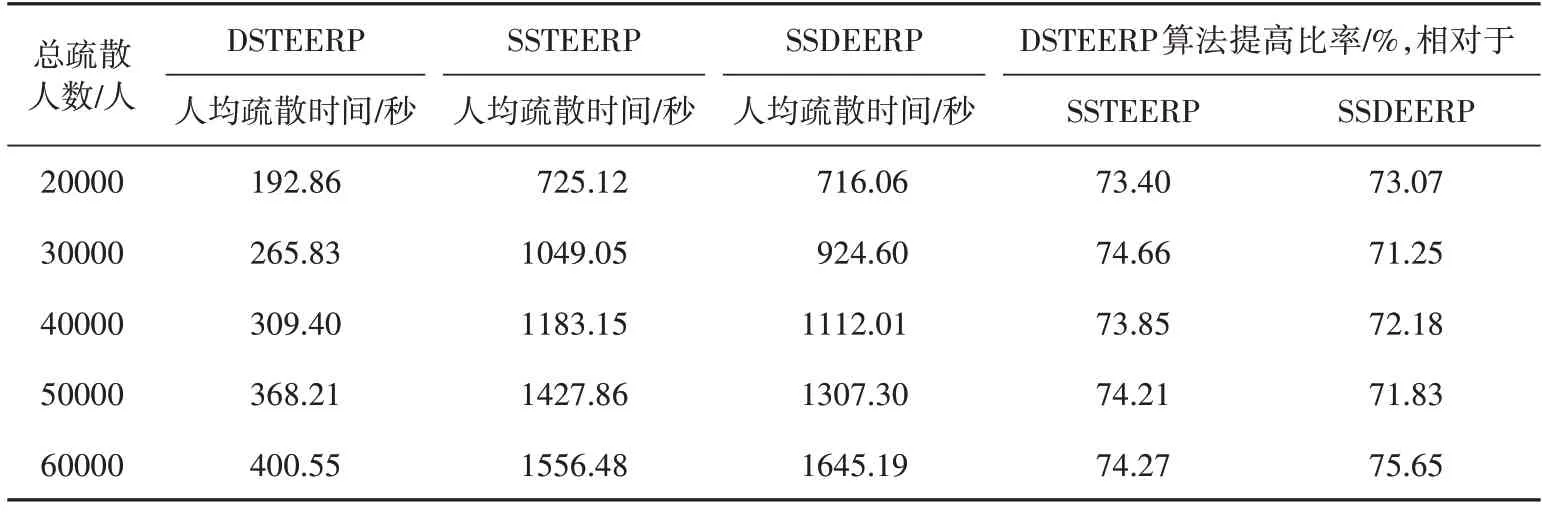
表5 广西大学西校区人均疏散时间结果比较

根据广西大学西校区内行人的疏散仿真结果，本文提出的DSTEERP 算法显著地提高了疏散效率。其中，当人群规模为6 万人时，DSTEERP 算法、SSTEERP 算法、SSDEERP 算法的总疏散时间分别为0.287 小时、1.259 小时、1.240 小时，人均疏散时间分别为0.111小时、0.432小时、0.457小时。总体来说，DSTEERP算法的总疏散时间比SSTEERP 算法减少75.24%以上，人均疏散时间减少73.40%以上；DSTEERP 算法的总疏散时间比SSDEERP 算法减少74.73%以上，人均疏散时间减少71.25%以上。即动态应急疏散路线规划算法与两个静态应急疏散路线规划算法相比，总疏散时间和人均疏散时间均减少70%以上。且随着人群规模的增大，DSTEERP 算法、SSTEERP 算法、SSDEERP 算法的总疏散时间和人均疏散时间都在随之增大。但是，本文提出的DSTEERP算法需要的疏散时间随人群规模的增长速度远低于SSTEERP 算法和SSDEERP 算法。从疏散时间的增长角度也说明了该算法的优越性。

上述两个仿真区域的应急疏散仿真结果表明，DSTEERP 算法的行人应急疏散总疏散时间和人均疏散时间远低于SSTEERP 算法、SSDEERP 算法，行人应急疏散效率更高。具体来说，青秀山风景区的仿真疏散结果表明，DSTEERP 算法与SSTEERP算法、SSDEERP算法相比，总疏散时间和人均疏散时间均减少40%以上；广西大学西校区的仿真疏散结果表明，DSTEERP 算法与SSTEERP 算法、SSDEERP算法相比，总疏散时间和人均疏散时间均减少70%以上。

4 结论与展望

4.1 研究结论

本文提出了一种基于实时路网数据和Dijkstra 算法的景区行人动态应急疏散路线规划算法，该算法同时考虑了道路长度、宽度、坡度、实时人群密度等因素对行人疏散效率的影响，更符合行人实际疏散情形。通过对南宁市青秀山风景区和广西大学西校区进行仿真模拟和疏散效率结果比较，本文得出如下结论：

（1）与静态行人应急疏散路线规划相比，动态行人应急疏散路线规划的疏散效率更高。在静态行人应急疏散路线规划中，行人均按照初始路网数据下的最优应急疏散路线疏散，但是随着疏散活动的进行，大量行人同时朝同一安全出口移动，极易导致某些道路人群密度增大，疏散速度减小，疏散效率降低。而本文提出的DSTEERP 算法能根据实时路网数据有效分流疏散行人，降低道路人群密度，提高疏散效率。

（2）DSTEERP 算法在广西大学西校区的提升效果更加显著。仿真疏散结果表明，广西大学西校区的行人疏散效率提升比例比青秀山风景区高20%以上，该结果的形成可能有两个原因：一是路网密度的差异。根据路网拓扑结构图和计算结果可知，广西大学西校区的路网密度较大，是青秀山风景区的2.47 倍。道路发生拥堵时，路网密度较大的区域可供疏散的道路较多，采用动态疏散路线规划算法能及时优化和调整路线，算法的积极作用更加显著；而路网密度较小的区域可供疏散的道路较少，动态疏散路线规划算法的线路优化作用效果相对较小。因此在路网密度大的区域采用动态行人应急疏散线路规划的行人应急疏散提升效果更为突出。二是海拔高度差的差异。广西大学西校区地势平坦，海拔高度差近乎为0，而青秀山风景区为山地景区，海拔高度差较大。海拔高度差较大的区域行人步行速度较慢，人群疏散更为缓慢，这也在一定程度上影响动态疏散路线规划算法的优化效果。

4.2 管理启示

（1）提前制定动态应急疏散预案。科学高效的行人应急疏散预案可以缩短疏散时间，避免不必要的拥堵和二次伤害。节假日期间热点景区人流密集，极易发生拥堵。为避免人员伤亡和财产损失，景区应提前制定行人应急疏散预案。而本文提出的DSTEERP算法能显著提高行人应急疏散效率，可以为景区管理部门制定行人应急疏散预案提供参考。

（2）定期开展行人动态疏散演练。景区管理部门应定期开展各类行人动态应急疏散演练和培训，建立常态化机制。一方面要提升景区工作人员遭遇突发情况需要应急疏散的应对能力，另一方面也要提高游客的灾害逃生能力与自救能力，使景区工作人员和旅游者在突发情况发生时能够从容应对，避免出现因过度恐慌而影响整体疏散效率的情形。

（3）大力实施动态应急疏散措施。突发公共事件下景区应根据动态应急疏散预案及时疏散游客，完善与游客的双向沟通机制，通过手机、特定系统或广播等途径将结合实时路网数据调整的动态应急疏散路线推荐给游客，积极引导游客疏散，提高疏散效率，避免不必要的拥堵和二次伤害。

（4）积极推进景区智慧化建设。大力推进景区智慧化管理平台的建设和应用推广，通过智慧化管理平台实时获取游客位置信息，应用动态行人应急仿真疏散算法规划行人应急疏散或出行路线，为游客的应急疏散和观光游览等提供最优化的路径选择。同时，智慧化管理平台还能为游客提供在线预约、虚拟排队、智能导览、出游攻略、美食推荐等服务，有助于提升景区管理水平和服务质量，提高游客旅游满意度。

4.3 研究局限与未来研究方向

本文仍存在一定的局限性：一是本文并未区分道路类型，忽略了不同类型的道路对行人动态应急疏散的影响，而且为便于研究，本文将景区内道路路网抽象为边和节点的拓扑结构，将弯曲道路近似看作直线，将同一道路上宽度、坡度、人群密度和疏散速度视为相同，属于理想状态下的假设，未来的研究可以进一步探讨同时考虑道路的长度、宽度、坡度、人群密度和道路类型的行人应急疏散效率，探讨弯曲道路的应急疏散路线规划算法等问题；二是本文仅考虑了行人应急疏散，没有考虑车辆和行人同时疏散的情况，而景区内一般有观光车辆可供疏散游客，未来的研究可以考虑将行人、观光车、私家车等多种疏散方式纳入算法；三是本文没有对疏散个体的疏散选择行为进行区分，在实际疏散中，即使面对相同的疏散环境，不同游客也可能具有不同的疏散选择，未来的研究可以进一步考虑不同个体的心理特征、身体素质和行为偏好等因素对行人动态应急疏散的影响。