A cooperative detection game: UAV swarm vs.one fast intruder

XIAO Zhiwen and FU Xiaowei

School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710129, China

Abstract: This paper studies a special defense game using unmanned aerial vehicle (UAV) swarm against a fast intruder.The fast intruder applies an offensive strategy based on the artificial potential field method and Apollonius circle to scout a certain destination.As defenders, the UAVs are arranged into three layers: the forward layer, the midfield layer and the back layer.The co-defense mechanism, including the role derivation method of UAV swarm and a guidance law based on the co-defense front point, is introduced for UAV swarm to co-detect the intruder.Besides, five formations are designed for comparative analysis when ten UAVs are applied.Through Monte Carlo experiments and ablation experiment, the effectiveness of the proposed co-defense method has been verified.

Keywords: cooperative detection game, unmanned aerial vehicle (UAV) swarm, fast intruder, defensive strategy, co-defense mechanism.

1.Introduction

With the development of modern unmanned technology,unmanned aerial vehicles (UAVs) have been extensively utilized in compelling various applications, as hazard warning, border patrol, and surveillance relying on their pleasant features of convenient deployment and low cost[1,2].Especially in recent years, tasks such as target detection, tracking and positioning based on UAV swarms [3,4] have become hot topics in the field of cooperative control [5-11].However, there is still a lot of room for research on how to use the numerical advantages of the UAV swarm to compensate for its lack of capabilities,such as maneuverability.

The pursuit-evasion game of multiple pursuers and one fast evader provides a solution to this problem to some extent.Isaacs [12] gave important factors that affect the success rate of capturing a fast evader: the initial formation of pursuers and the strategy of opposing both sides.Wang et al.[13] used a hierarchy framework to break down the complex pursuit-evasion game with multiplayer into various small-scale games and proposed a pursuing strategy based on formation control.Jin et al.[14] used Apollonius circle to design the strategy for evader to escape or to extend the capture time.Other research in this field [15-17] also provides various methods to capture the evader.

While pursuit-evasion game offers many interesting ideas to against a fast evader, the premise is that the UAV has the ability to capture the evader.When this condition is not met, target tracking may be another solution.Kada et al.[18] proposed a distributed model predictive control for cooperative multiple UAVs motion control.Koohifar et al.[19] decomposed the challenge of tracking a moving intermittent radio frequency source into two distinct phases of path planning and estimation.Zhang et al.[20] proposed a cooperative tracking scheme for multiple fixed-wing UAVs to track an uncooperative moving target.Brown et al.[21-23] studied the impact of initial swarm formation and proposed a predictive tracking method and a guidance law for UAV swarm to track a high capability malicious UAV.

In this paper, we propose a cooperative detection game combing pursuit-evasion game with target tracking problems.A co-defense mechanism is introduced for UAV swarm and verified by the simulation result.This paper has the following organization.Section 2 gives the basic conception of the problem.The kinematic model, detection model and communication model are also presented.Section 3 introduces the intruder’s offensive strategy,including the avoidance strategy and the break-through strategy.Section 4 introduces the co-defense mechanism of UAV swarm, including role derivation method and a novel guidance law.Section 5 introduces the formation design method, demonstrates and analyzes the performance of the proposed method through simulation.On this basis, the defense effect of UAV swarm under different formations is compared by the Monte Carlo experiment and the ablation experiment.Section 6 presents our conclusions and areas for further research.

2.Preliminaries

The schematic of the cooperative detection game is shown in Fig.1.A fast intruder comes from an unknown direction constrained by α and scout a hypothetical target atOwhile avoid collisions with any UAV.The task of UAV swarm is to co-detect the intruder as long as possible.

Fig.1 Schematic of the cooperative detection game

2.1 Kinematic model

The UAVs and the intruder are assumed to fly at a constant speed, and the motion equation can be established as follows:

wherex,yrepresent the position of this aircraft,vis the speed, φ represents its current heading, ∆φ represents the heading increment per unit time ∆t.According to the basic principle of aerodynamics, the turning radius of the aircraft can be obtained by

wherenyrepresentstheoverloadofthe aircraft,gis the accelerationofgravity.Asshown in Fig.2,theaircraft turns fromAtoA′, and the heading increment is ∆φ.

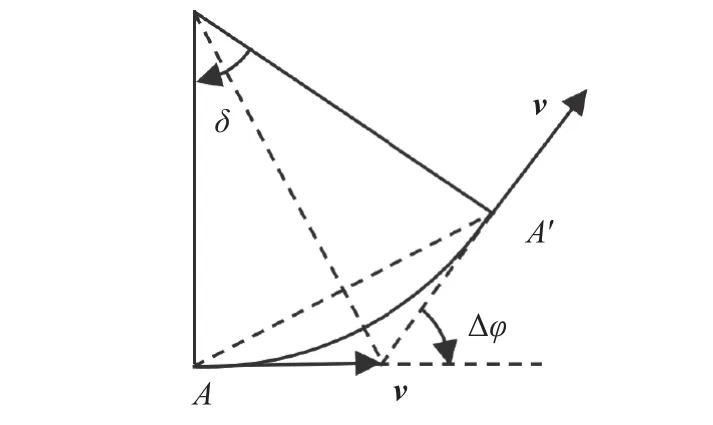
Fig.2 Schematic of the aircraft turning process

In Fig.2, δ represents the center angle corresponding to the flight trajectory.∆φmaxcan be obtained by

2.2 Detection range and threat angle

Assuming that the position and velocity information of the targets in the detection range can be instantly obtained by the detection equipment on the airplane.The detection range of a UAV is shown in Fig.3.This area has a sector shape with an angle equal to 120◦, andPradiusrepresents the radius of the UAV’s detection range.

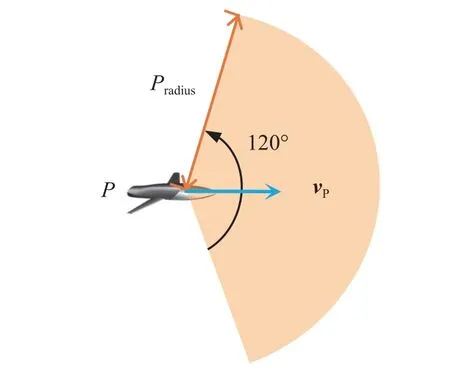
Fig.3 Schematic of the UAV’s detection range

If there is a UAV enters the detection range of the intruderE, the angle ∠GPE can be applied to assess whether the UAV poses threat to the intruder.

In Fig.4,Eradiusrepresents the radius of the intruder’s detection range.PG is parallel to EF, and the angle limited by them is defined as the threat angle φt.AsPmoves towards EF, the probability of the intruder being collided will increase.Therefore, φtcan be defined as the threat angle, which indicates the threatening UAV.

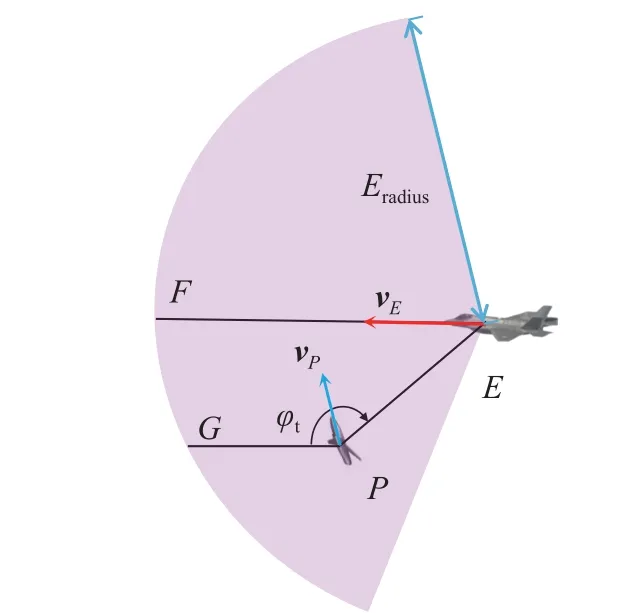
Fig.4 Schematic of the intruder’s detection range and the threat angle

2.3 Communication mechanism

The communication mechanism in this paper is relatively simple.As shown in Fig.5, the communication range has a circle shape with fixed radiusRcomm.P1can communicate withP2, but cannot transform any information toP3.There is no time delay in the information delivery process, and the communication burden caused by the amount of data is not considered.This provides convenience for the research on the cooperative detection method of the UAV swarm in this paper.

Fig.5 Schematic of the UAV’s communication range

3.Offensive strategy

When a threatening UAV appears in the intruder’s detection range, the intruder evades the UAV.This is an avoidance strategy.To make it more aggressive, the intruder applies the Apollonius circle to find a ‘gap’ among threatening UAVs.This is a break-through strategy.The intruder will change the offensive strategy based on the number of threatening UAVs in its detection range.

3.1 Avoidance strategy

The artificial potential field method is used to circumvent the UAV swarm for the fast intruder.

As shown in Fig.6,P1,P2andP3are in the detection range of the fast intruder.disEPiand θirepresent the distance and azimuth from intruder toPirespectively.

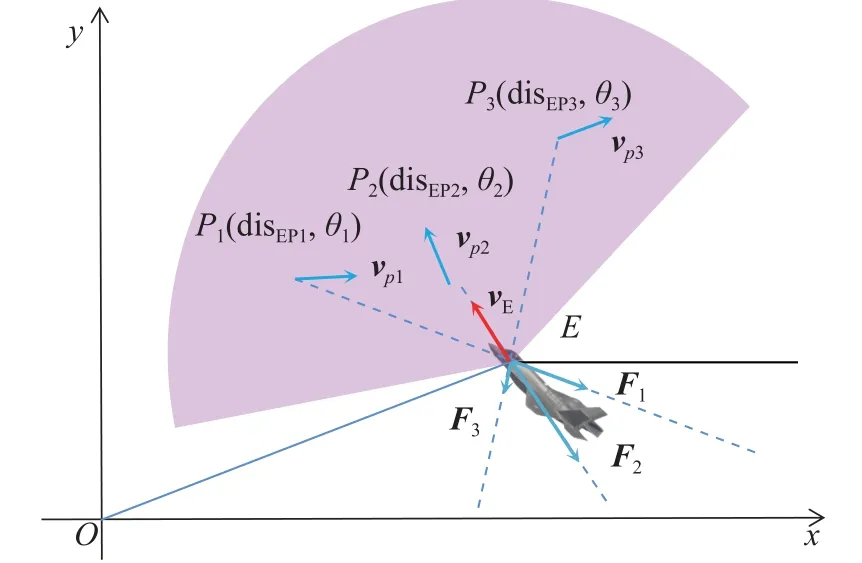
Fig.6 Schematic of artificial potential field method

According to the previous rules,P1andP2are regarded as the threatening UAVs.P3is flying away from the intruder.Therefore, the intruder will consider the repulsion caused byP1andP2at this moment.According to the artificial potential field theory, the intruder in Fig.6 will change the direction of its motion according to the combined forceF1+F2.When there arenthreatening UAVs in the same situation likeP1orP2,the combined repulsion of UAVs to the fast intruder is given by

whereFXandFYare the fractions of the combined force along thexandyaxis, respectively,k frepresents the force between the fast intruder and the UAV.

3.2 Break-through strategy

The break-through strategy is based on the geometric concept, which is known as Apollonius circle [24-26]and is widely used in the research of pursuit-evasion games.Asshown inFig.7,(xP,yP) represents the location of UAVP, (xE,yE)isthelocation of theintruderE,AandBare tangent points fromEto the Apollonius circleQ.It can be proven thatEwill always be intercepted by the defender when the intruder moves straight toward the inescapable area not covered by the orange dotted line [14].

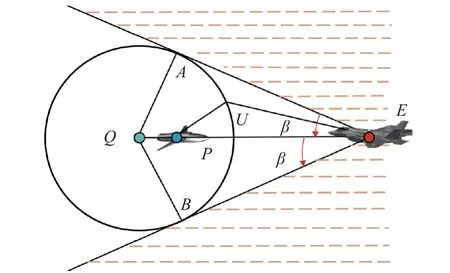
Fig.7 Schematic of inescapable area generated by Apollonius circle

It can be seen that the inescapable area can be described by β, and this provides a possible way for the intruder to find a shortcut.The shaded part in Fig.8,which is named as ‘gap’, allows the intruder to break through effectively [15].

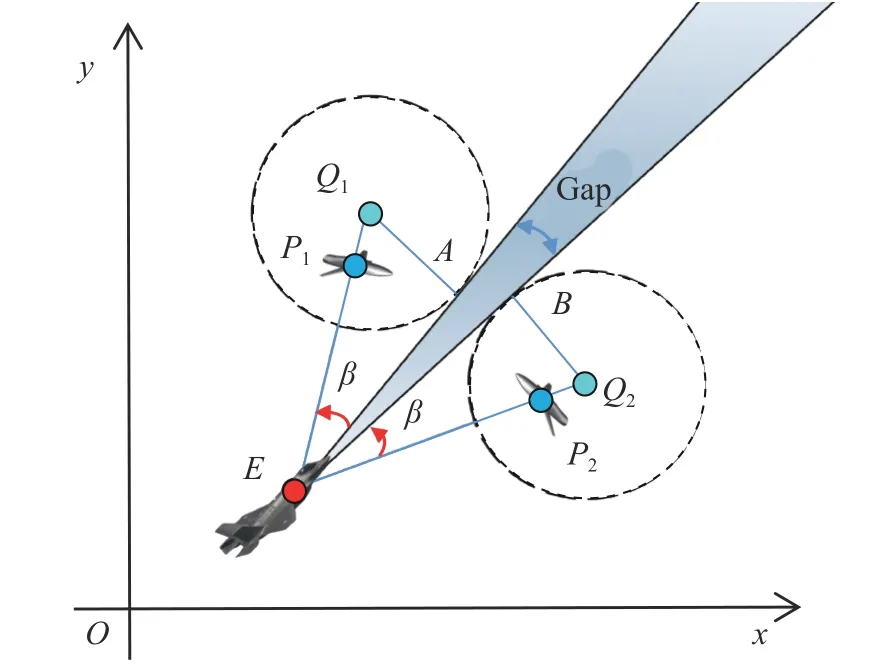
Fig.8 Gap and the better break-through direction

The avoidance strategy helps the intruder to evade the UAVs, while the break-through strategy provides a faster path for the intruder.The constraints of applying the offensive strategy are shown in Fig.9.

Fig.9 Offensive strategy of the fast intruder

4.Defensive strategy

In a football game, it is difficult for a defensive player to successfully defend a more capable offensive player.However, through teamwork among defenders, the probability of intercepting the offensive player can be greatly improved.This kind of behavior is known as the codefense mechanism.Although this mechanism cannot guarantee the 100% interception of offensive players, it usually helps the defender to slow down the offensive rhythm and increase the possibilities of subsequent counterattacks.

In this paper, the fast intruder can be regarded as the offensive football player with faster speed and stronger dribbling ability.And the UAV swarm need to apply the defensive strategy to disrupt the intruder and maximize the detection duration.As shown in Fig.10, the UAVs are named after their respective layers, including UAVf(the forward layer), UAVm(the midfield layer) and UAVb(the back layer).The UAVs in the same layer can communicate freely in the designed formation to react to the intruder in time and deploy the corresponding defensive strategy.The specific patrol trajectory in the initial state is illustrated in Fig.11.

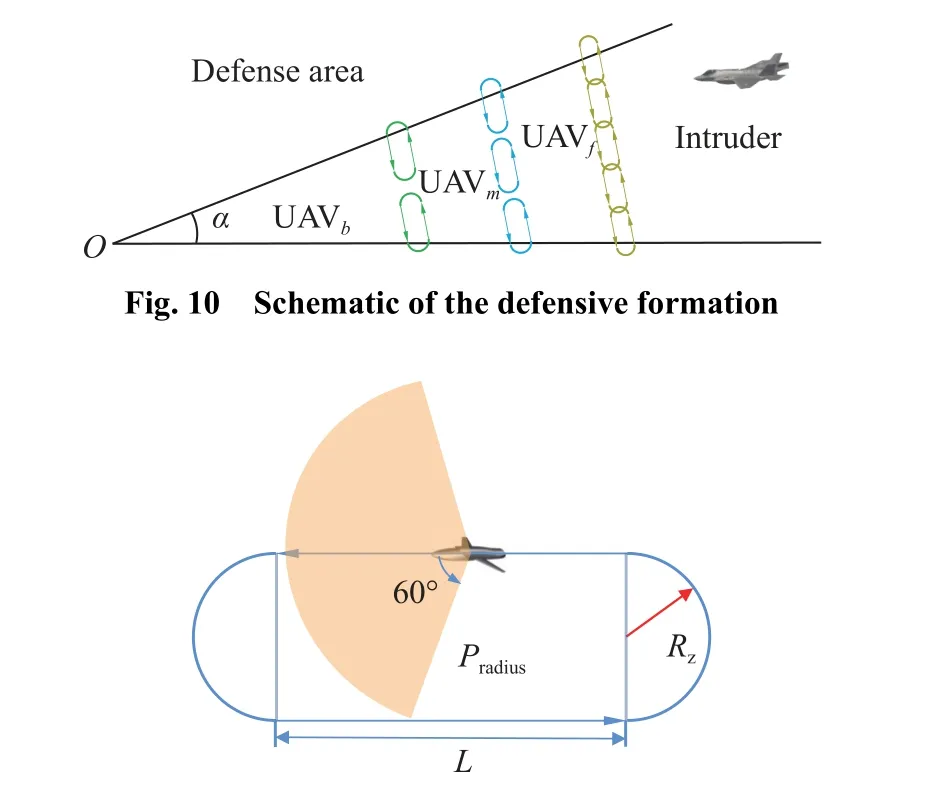
Fig.11 Schematic of UAV patrol trajectory

In Fig.11,RZis the turning radius, the length of straight lineLis determined by the size of the defense area.If a UAV detects the intruder or receives the location information of the intruder, the UAVs within its communication range will share the information and gain roles according to the co-defense mechanism.Based on this, each layer will have a UAV that will be assigned a special mission.They have different subscripts, where UAVstis named after the striker, UAVasplays the auxiliary role as an assist, and UAVcddoes the final “entanglement” with the intruder in the final stage.

As shown in Fig.12, UAVstis the first UAV that spots the intruder, and it will track the intruder directly.Other UAVfwill move towards the destination of the intruder so that the UAVmcan react as early as possible.Information containing the location and speed of the intruder will be passed by these UAVf, and this scenario also occurs in the process of transmitting information from UAVmto UAVb.

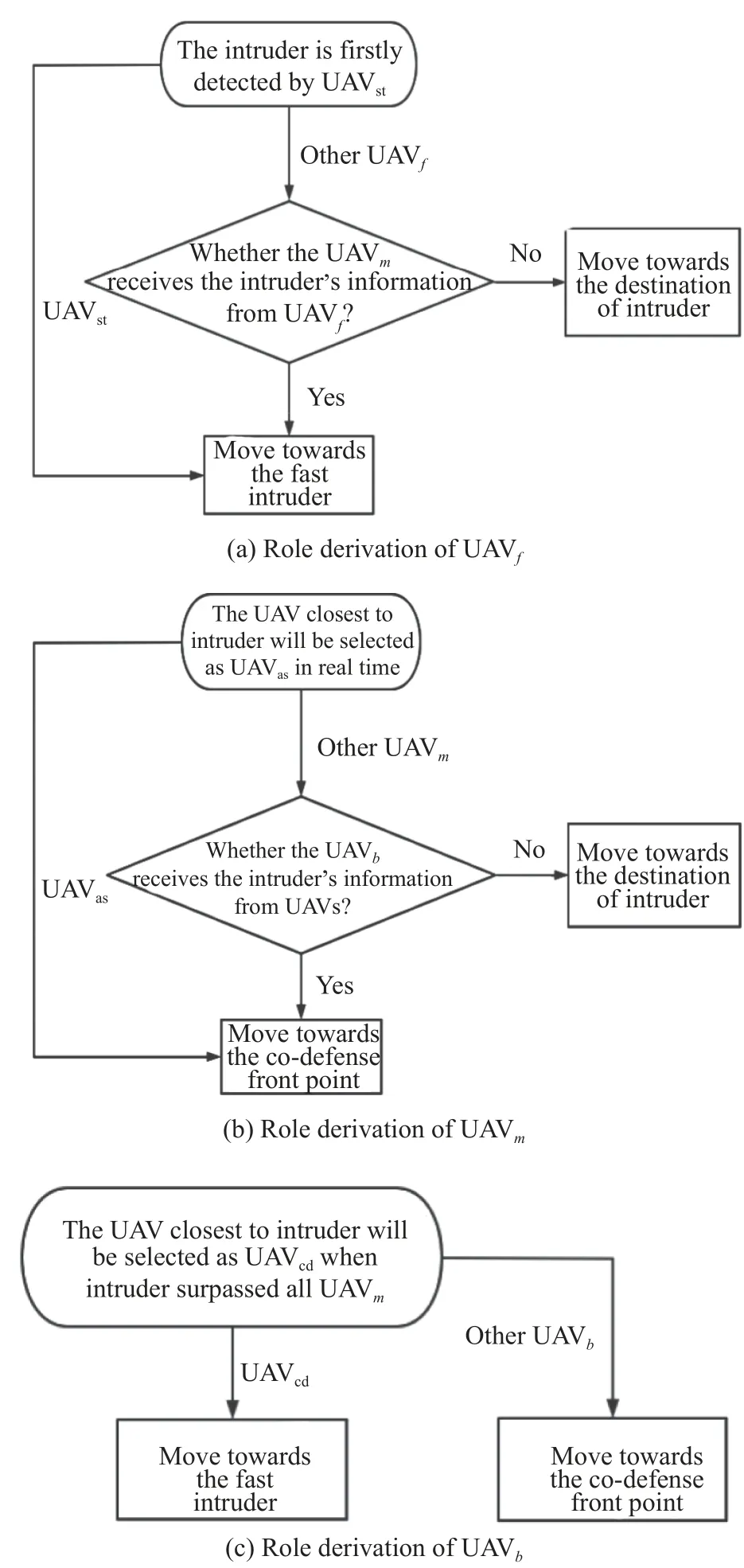
Fig.12 Role derivation for UAV swarm

It is worth noting that the role of UAVstand UAVcdwill remain the same to ensure the continuous detection of the intruder at both early and late stages.While the UAVasis determined in real time and directly moves to codefense front point, which is a novel guidance method based on the traditional guidance law combined with the Dubins curve [27-30].

As is shown in Fig.13, the intruder flies in the current direction and arrives atE′afterT.φErepresents the heading of the intruder, disEPrepresents the distance of EP.In this process, UAV is expected to fly fromPtoP′,and points toE′.If the distance of E′P′is equal toPradius,E′will be defined as the co-defense front point.The Dubins curve is then used to calculate the shortest flight timeTPfor UAV flying fromPtoP′.Therefore, the problem will be transformed into finding a suitableTP,and letTP=T.

Fig.13 Schematic of co-defense front point

Fig.14 illustrates a possible situation of Dubins curve for path planning, whereRZminis the minimum turning radius, θ1and θ2represent the angle that the UAV passes through in a circular motion.

Fig.14 Schematic of the UAV’s shortest path

Else returnTdas the shortest time and corresponding position of co-defense front point.

SolvingTby numerical methods, the UAV can find a front point as its expected direction.However, the codefense front point will be applied only when the following conditions are met:

(i) The distance from the intruder to its destination is greater than or equal to the distance from the UAV to the intruder’s destination;

(ii) The UAV is not on the extended line of the intruder speed direction.

Otherwise, co-defense front point will be simply set to

where (xE,yE) represents the position of the intruder andis a constant set for this special case.

5.Simulation

5.1 Formation design

The UAVs in each layer are evenly distributed at the bottom of the isosceles triangle (the defensive area).nf,nmandnbrepresent the number of UAVs in each layer.Rf,RmandRbare the anterior distances of UAVs in each layer.The distance between each layer of UAV is limited by the size of the defense area, including the anterior distance and α.Five initial formations of UAV swarm are presented in Fig.15.

In Fig.15, the yellow circles represent the UAVf, the blue circles represent the UAVm, and the green circles represent the UAVb.Fig.16 takes formation 5-3-2 as an example to describe the initial state and related parameters of the UAV swarm.

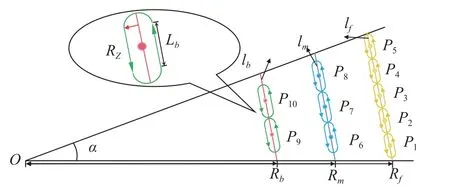
Fig.16 Schematic diagram of formation 5-3-2

In Fig.16,lf,lmandlbindicate the length of the defensive area in each layer,Lf,LmandLbare the length of the straight flight part of each patrol UAV.In this way,the initial position of the UAVfcan be calculated by

where 1 ≤i≤nf.

The initial position of the UAVmis determined by

The initial position of the UAVbare given by

5.2 Experiment 1: demonstration

According to expert experience, the parameters of the detection game are shown in Table 1.

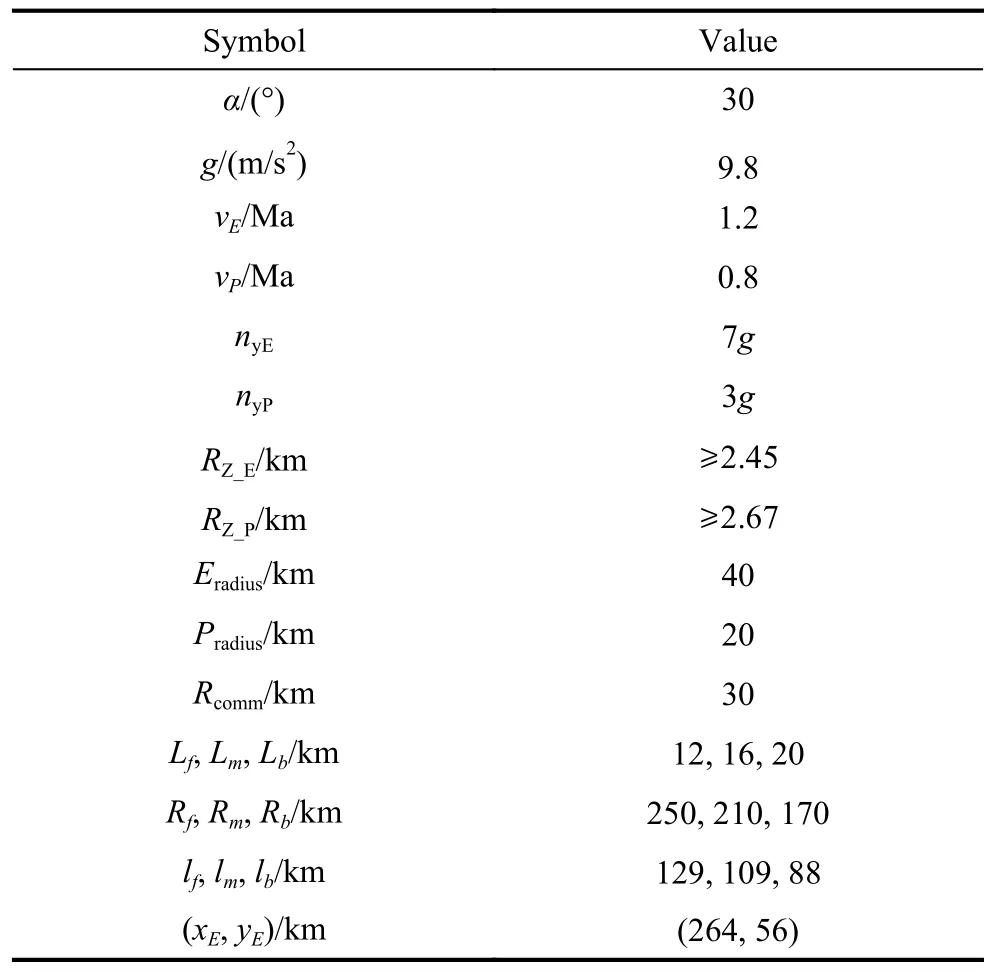
Table 1 Parameters

Fig.17 shows the simulation snapshots of formation 5-3-2.Fig.17(c) and Fig.17(d) show the moment when the communication between different layers of UAVs is established.Fig.17(d), Fig.17(e), Fig.17(g)show the guidance process of different UAVs (P6,P7,P10) using the co-defense front point, respectively.In order to make the results more concise and clear,some information is not shown in the figure.For example, in Fig.17(e), Fig.17(f), Fig.17(g), only the movement trajectories of different layers of UAVs at the corresponding moment are reserved.The hierarchical distribution of the detection trajectories in Fig.17(h),as well as the position of the end of the same color trajectories, all illustrate the effectiveness of the co-defense mechanism.It can be seen that the UAV swarm achieves long-term tracking and detection of the fast intruder through initial defensive formation and the co-defense mechanism.

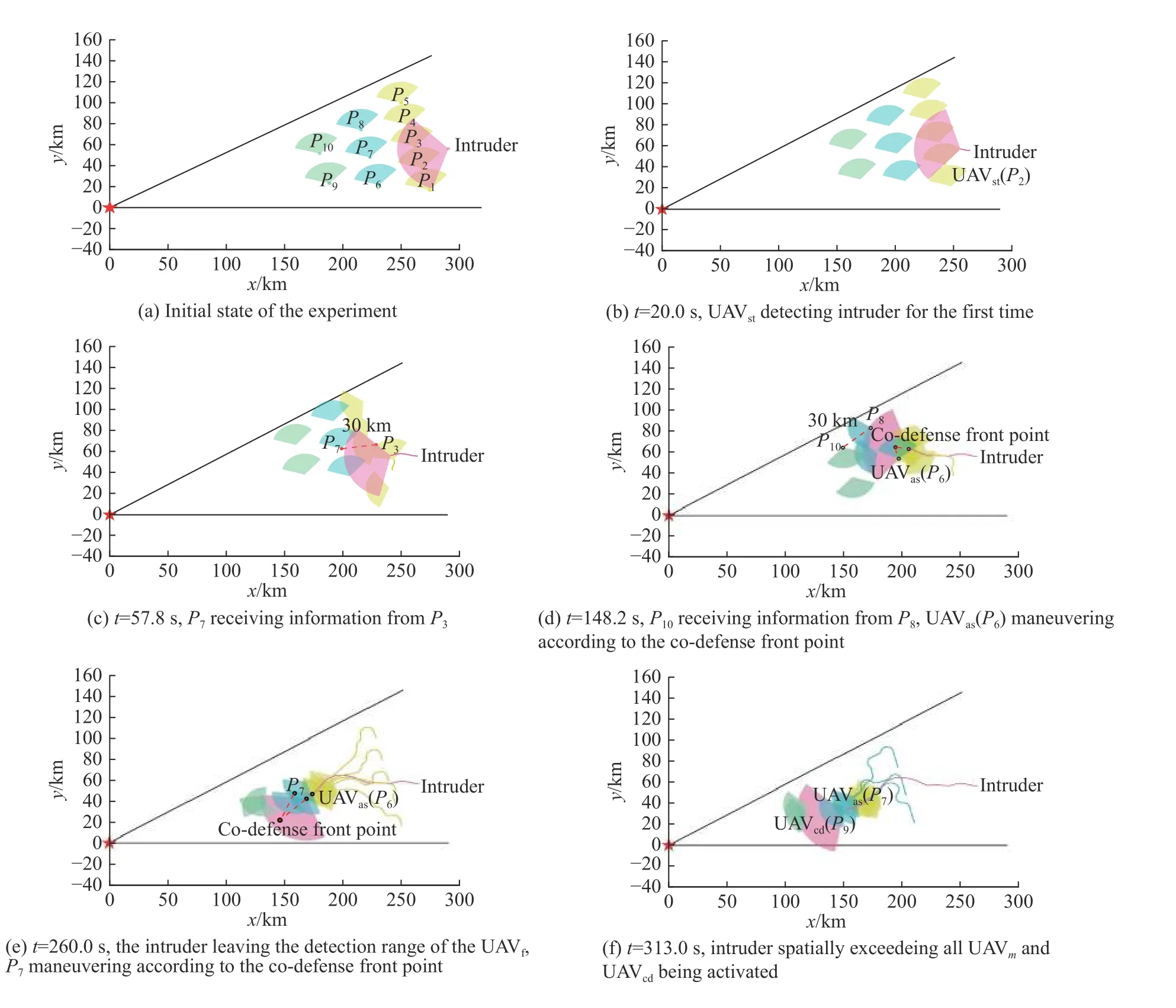
Fig.17 Snapshots of the result (formation 5-3-2)

5.3 Experiment 2: Monte Carlo

The previous section illustrates the process of cooperative detection game when applying the formation 5-3-2.This section will further compare the five formations by changing the initial position and speed of the intruder via the Monte Carlo method.

Firstly, the initial position of the intruder will be randomly generated.The discovery duration and the time of the first discovery are calculated to measure the defense effect of each formation.Table 2 shows the average of the results after 500 rounds of simulation.

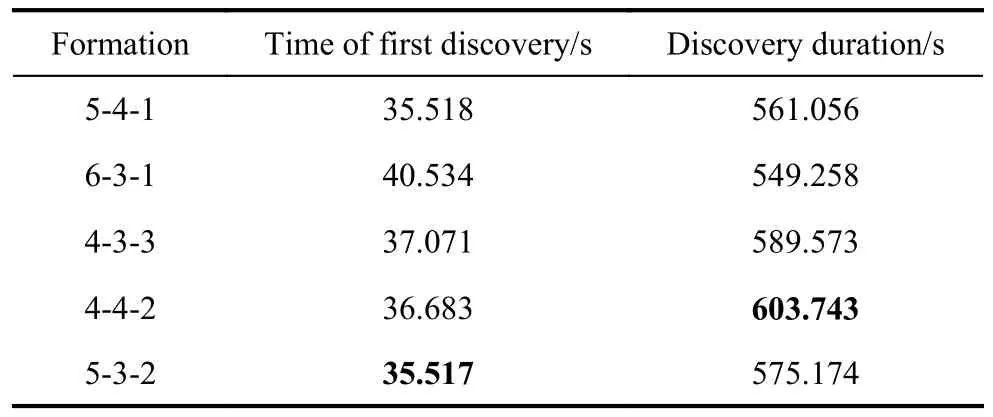
Table 2 Simulation results when the invaders are born in different positions (500 rounds)

In Table 2, the formation 4-4-2 has the longest averaged discovery duration and the formation 5-3-2 has the smallest average time of the first discovery.

On this basis, we further compare the performance of different formations in the cooperative detection game by increasing the speed of the intruder.

Fig.18 and Fig.19 illustrate the distribution of the discovery duration and the time of the first discovery in each case.Each box represents 25% to 75% of the data in the group, the horizontal line represents the median, and the dot represents the average value of this group of data.

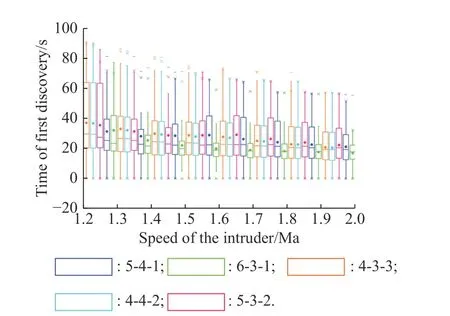
Fig.18 Box diagram of the first discovery time in the five formations

Fig.19 Box diagram of the average discovery duration in the five formations

By calculating the average of each set of test data, the averaged discovery durationTiand the averaged time of the first discoveryTfdiare shown in Table 3, whereirepresents the serial number of each formation.

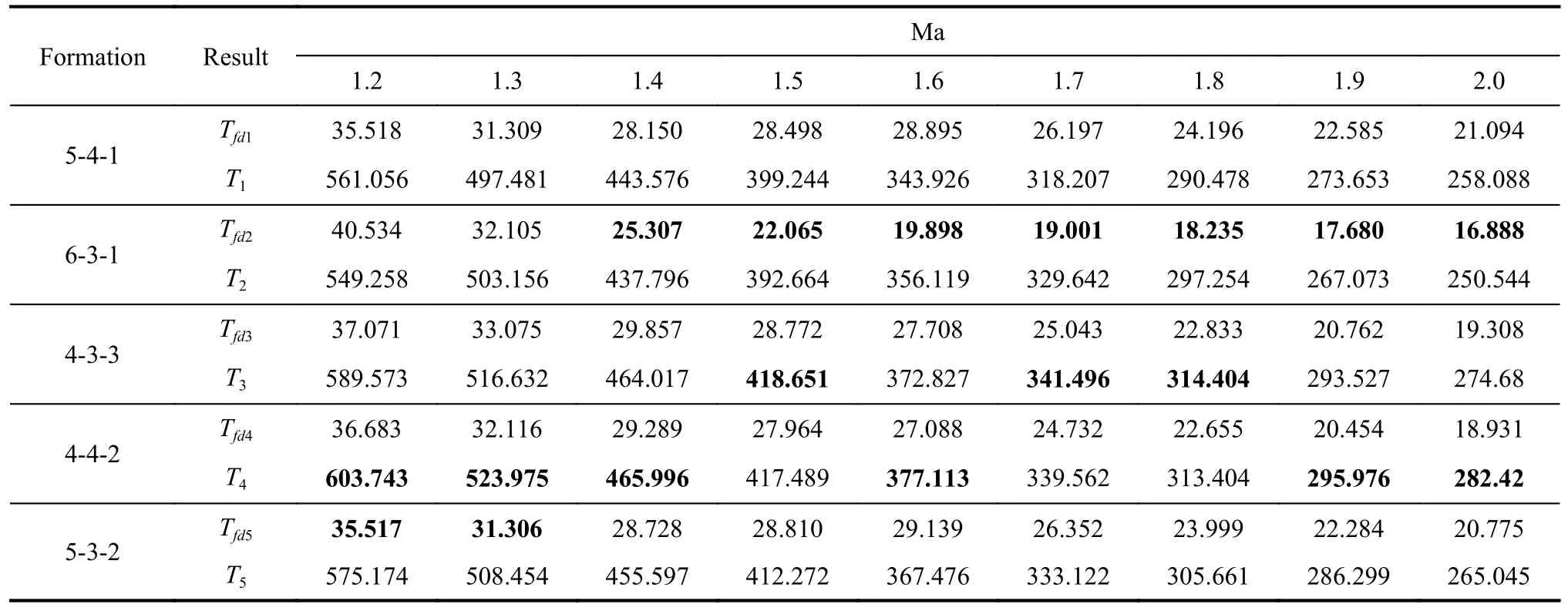
Table 3 Simulation results of the intruder at different speeds (500 rounds) s

It can be seen that formation 6-3-1 has the minimum averaged time of the first discovery, while formations 4-4-2 and 4-3-3 have a good performance in continuously detecting the intruder.For each speed of the intrudervE, there exists the minimumTiand the maximumTfdi, which will be represented as min(Ti) and max(Tfdi)respectively.To further highlight the capability of these formations, (13) is designed as follows:

where [·]vEis a conditional operator, the expression inside is the normalized time with other formations as reference.In this way, Score1and Score2could be applied as the capability metrics for each formation while taking into account the speed of the intruder.Obviously, the maximum value for Score1and Score2is 9.And the final scores are shown in Table 4.

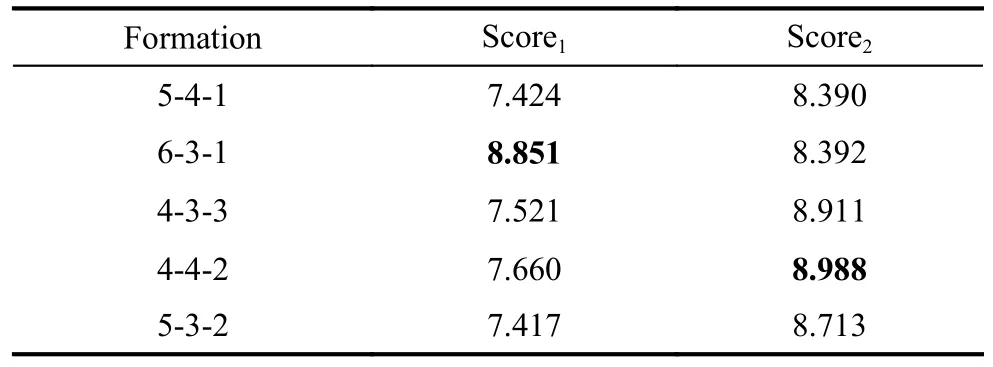
Table 4 Scores of each formation

Formation 6-3-1 has the highest Score1(8.851) and formation 4-4-2 has the highest Score2(8.988).Objectively,if only considering the early detection of intruders, a sufficient number of UAVs on the outermost layer would be a good choice.However, considering the insufficient number of UAVs, the rational design of the UAV formation in the middle and outer layers will have a key impact on the detection duration.Surprisingly, the performance of the formations 4-4-2 and 4-3-3 on Score2coincides with two important formations in football.

5.4 Experiment 3: ablation experiment

The essence of the ablation experiment is comparison, by removing a module from the algorithm to study the effect of that module on the performance of the algorithm.Based on the co-defense mechanism proposed in this paper, the following three cases will be compared via the Monte Carlo method.

Case 1: With the proposed mechanism and guidance law.UAVs use complete co-defense mechanism to participate in the cooperative detection game, and the codefense front point is applied as the guidance law.

Case 2: Without the proposed guidance law.UAVs complete the cooperative detection game under the codefense mechanism, while the guidance law based on the co-defense front point has been replaced by the pure tracking method.

Case 3: Without the co-defense mechanism.UAVs only use the pure tracking method to track and detect the fast intruder, and the co-defense mechanism will not be applied.

Under the same settings as experiment 2 (Case 1), the Monte Carlo simulation of Case 2 and Case 3 is performed respectively.The average detection durationTiis used to measure the detection effect of the UAV swarm.

In order to visually represent the differences between different cases, the corresponding detection duration in different cases is divided and the proportional distribution is shown in Fig.20 and Fig.21.

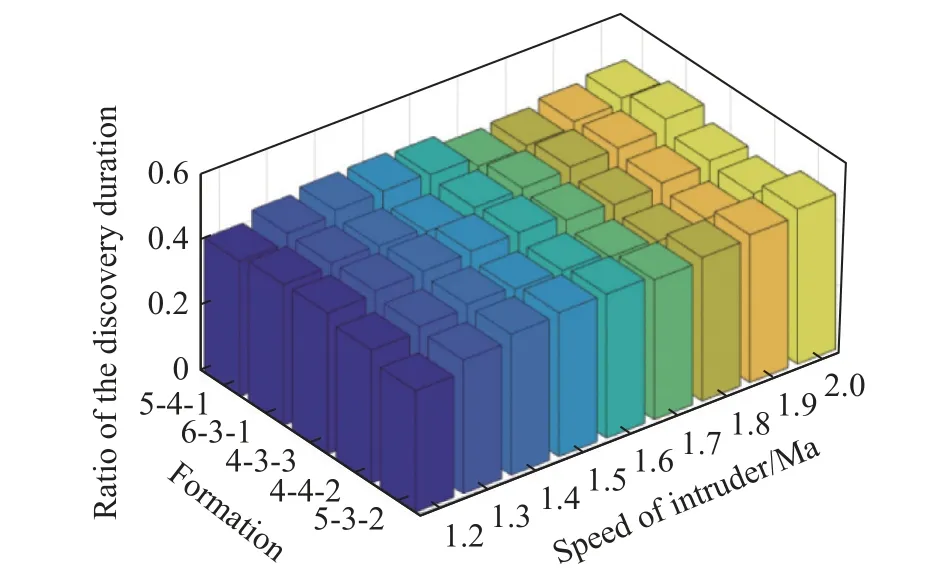
Fig.21 Proportional distribution of discovery duration (Case 3 vs.Case 1)

The ratio of discovery duration is less than 76.82% (the average is 58.23%) if the proposed guidance law is replaced by the pure tracking method.

The ratio of discovery duration is less than 48.46% (the average is 43.62%) if the co-defense mechanism is not applied.

The experimental results show that the guidance law and the co-defense mechanism proposed in this paper improve the defensive ability and defense effect of UAV swarm.

6.Conclusions

In this paper, a cooperative detection game of UAV swarm vs.one fast intruder is studied, where the intruder needs to bypass UAVs to reach its destination, and the UAV swarm needs to track and detect the intruder as long as possible.Based on the establishment of basic scenarios and models, strategies and methods are designed for the intruder and the defender (UAV swarm), respectively.

The avoidance strategy based on the artificial potential field and the break-through strategy based on Apollonius circle are proposed for the fast intruder.For defenders,this paper proposes a formation design method, as well as a co-defense mechanism composed of a role derivation method and a co-defense front point based guidance law.

In the experimental stage, the formation 5-3-2 is used as an example to demonstrate the process of the cooperative detection game.According to the Monte Carlo method and the proposed evaluation method, the defensive effect of the UAV swarm under different formations is compared.Finally, the results of the ablation experiment prove the effectiveness of the proposed method in this paper.

In the future, the co-defense mechanism proposed in this paper will be further optimized on the basis of increasing the number of intruders and improving the intelligence of the offensive strategy.At the same time, it is expected to apply the co-defense mechanism proposed to more application scenarios, and use the deep reinforcement learning method to solve the cooperative detection problem.