Minimum-energy leader-following formation of distributed multiagent systems with communication constraints
2024-01-17QINDonghaoWANGLeGAOJiuanandXIJianxiang
QIN Donghao, WANG Le, GAO Jiuan, and XI Jianxiang
Rocket Force University of Engineering, Xi’an 710025, China
Abstract: This paper concerns minimum-energy leader-following formation design and analysis problems of distributed multiagent systems (DMASs) subjected to randomly switching topologies and aperiodic communication pauses.The critical feature of this paper is that the energy consumption during the formation control process is restricted by the minimum-energy constraint in the sense of the linear matrix inequality.Firstly, the leader-following formation control protocol is proposed based on the relative state information of neighboring agents, where the total energy consumption is considered.Then, minimum-energy leader-following formation design and analysis criteria are presented in the form of the linear matrix inequality, which can be checked by the generalized eigenvalue method.Especially, the value of the minimum-energy constraint is determined.An illustrative simulation is provided to show the effectiveness of the main results.
Keywords: multi-agent system, leader-following formation,communication pause, minimum energy.
1.Introduction
Formation control of distributed multi-agent systems(DMASs) has shown an increased research interest in communities of control systems in recent years, which has a broad range of applications in various areas, such as multiple mobile robots [1,2], distributed sensor networks[3,4], unmanned aerial vehicles [5,6], and satellite groups[7-9].Now, many approaches have been developed for formation control problems, such as virtual-structurebased strategy [10], behavior-based strategy [11,12],leader-follower-based strategy [13], and consensus-based strategy [14,15], and so on.In [16], it was proved that the former three strategies are the special cases of the consensus-based formation strategy.
The cooperative formation can carry out various complex tasks with remarkable efficiency, wide coverage,strong fault tolerance, and high-level security, which is an important research direction of DMASs.Generally,according to the topology structure of DMAS, the cooperative formation can be categorized into two cases: the leaderless formation and the leader-following formation.Different from the leaderless formation control, the leaderfollowing formation control tries to guide the DMAS tracking a desired trajectory by using just a singular agent(or a subset of agents) that is called the leader(s), and other agents that are referred to as followers, which are driven with a time-varying (or time-invariant) geometric structure to track the leader(s).In [17], it was verified that the leader-following configuration can enhance the communication and orientation of the flock, and is also an energy saving mechanism in many biological systems.Leader-following formation problems of first-order multirobots with a virtual leader were studied in [18], where the desired trajectory was determined by the virtual leader.Brinon-Arranz et al.[19] investigated the elastic formation tracking problems for nonlinear multi-agent systems, where all the agents can converge to a circular motion with the center tracking a time-varying reference.In [20], the leader-following networked mobile robot formation problem with unknown slippage effects for collision avoidance was investigated.Yan et al.[21]addressed the observer-based time-varying leader-following formation problem for DMASs with the one-sided Lipschitz nonlinear and quadratic inner-boundedness nonlinear dynamics, which can guarantee less conservatism and more generality with large Lipschitz constants.
The whole interactions among the DMAS play critical roles for the formation achievement.When DMASs perform complex tasks, the interaction topology may be switched as required, which leads to interaction channels among agents to be on or off for an indefinite time interval.All the possible interaction topologies form a switching set for the DMAS to choose.In addition, due to sensor failure, electronic interference, data packet loss etc.,or to avoid enemy monitoring, there may be no any information transmission among all the agents in aperiodic time intervals, which are time stages of communication pauses.Generally speaking, it is of great significance to study communication constraints of the co-existence randomly switching topologies and aperiodic communication pauses for some specific applications.In [22], the time-varying formation control problem of singular multiagent systems with switching topologies was investigated based on the outputs of systems.Xi et al.[23]addressed the time-varying DMAS formation problems with the given energy constraint under the situation of switching topologies.In [24], a solution for the timeinvariant formation control problem of a single-mastermultislave bilateral teleoperator system in the presence of communication pauses was provided.Chai et al.[25] verified that the computation cost is greatly reduced for the fixed-time event-triggered time-varying formation tracking of leader-following DMASs with communication pauses than that with continuous time.
To reduce the energy consumption during the cooperative control process, a design index function of the energy consumption is usually constructed to be optimized.It is required that the index to be bounded for collaborative tasks, where the guaranteed-cost strategy is a typical one.Based on the linear quadratic regulator, Cao et al.[26]proposed two global cost functions for multivehicle systems: interaction-free and interaction-related cost functions.In [27], based on the linear matrix inequality method, guaranteed-cost consensus control criteria for general high-order DMASs with sampled-data information were given, and the corresponding guaranteed-cost values was obtained.Wang et al.[28] proposed scalable guaranteed-cost consensus design and analyzed criteria for general high-order multi-agent systems with time delays, and corresponding formulations of the upper bound of guaranteed-cost functions were derived.In [29],robustH∞guaranteed-cost time-varying DMAS formation problems with time-varying delays and external disturbances were investigated, and sufficient conditions withH∞disturbance attenuation performance were derived.However, the bounds derived in [26-29] may not be minimal.In general, it is a way to minimize energy consumption by designing reasonable energy constraints to restrict the upper bound value of guaranteed cost.Combining with above introductions of the formation, communication constraints, and guaranteed-cost strategy of DMASs, to the best of our knowledge, there are few literatures reported on the study of the minimum-energy leader-following formation with communication constraints of randomly switching topologies and aperiodic communication pauses.
In this paper, minimum-energy leader-following formation control problems for DMASs are investigated,which are subjected to communication constraints of randomly switching topologies and aperiodic communication pauses.By considering the local information from neighboring agents of the whole system, a distributed control protocol is proposed with the total energy consumption of all the agents being involved.With the state space decomposition method, the closed-loop system is divided into two subsystems, which correspond to the macroscopically whole motion of the DMAS and the microcosmically relative motion of followers, where the macroscopically whole motion can be regarded to be dictated by the leader.To minimize the total energy consumption during the formation process, minimum-energy criteria are presented to restrict the total energy consumption of the whole DMAS.By the criteria, it can not only guarantee the formation achievement but also ensure the energy consumption during the formation control process to be minimal in the sense of the linear matrix inequality.
The novelties and primary contributions of this paper are listed as follows.(i) Problems of minimum-energy consumption for leader-following formation are studied,while the guaranteed-cost strategy proposed in [26-29]cannot ensure the total energy consumption during the cooperative control to be minimal.By the constructed constraint for restricting the energy consumption to be minimal, an additional linear matrix is derived as an important term of minimum-energy formation criteria.The criteria can be checked by the generalized eigenvalue method.(ii) Communication constraints of the coexistence of randomly switching topology and aperiodic communication pauses are dealt with, while DMAS formation problems in the case of either switching topologies or communication pauses are studied in [22-25,30].In this study, the whole time is modeled as time intervals by time intervals, where each interval contains two subintervals, and the convergent quantity of the constructed Lyapunov function candidate in the switching topology subinterval is required to be greater than the divergent quantity in the communication pause subinterval in each interval.Thus, the global convergence can be ensured and the leader-follow formation is achievable.
The rest arrangement of this paper is structured as follows.Section 2 introduces some preliminaries and the problem description.Design and analysis criteria of the minimum-energy leader-following formation are proposed in Section 3.In Section 4, a numerical example is given to show the effectiveness of the theoretical results.Section 5 summarizes the whole work of this paper.

2.Preliminaries and problem description
2.1 Graph theory

2.2 Communication constraints


This paper investigates the leader-following DMAS formation problem with randomly switching topologies and aperiodic communication pauses.In the leader-following DMAS, the interconnected channels among followers are bidirectional with the same weight, but they are unidirectional from the leader to followers, which imply that the leader can send information to followers but does not receive information from followers.Therefore, the Laplacian matrix of the topology of the leaderfollowing DMAS is asymmetric.Moreover, it is assumed that there is at least one spanning tree in each topology graph of the switching set, where the leader is assigned as the root node in the topology graph.
2.3 Problem description
Consider a leader-following DMAS withNagents, where agent 1 is assigned as the leader and agenti(i=2,3,···,N)are followers.The dynamics of leader and agenti(i=2,3,···,N) are described as

wherei=2,3,···,N,p∈N,fi(t)∈Rdis a piecewise con-

The main objective of this paper focuses on two problems as follows: (i) Determine the gain matrixKsuch that leader-following DMAS (1) with control protocol (2)can achieve the minimum-energy time-varying formation.(ii) Propose sufficient conditions of the minimum-energy leader-following formation achievement when the gain matrixKis given in advance.Main difficulties lie in how to determine the minimum-energy constraint of the leaderfollowing DMAS with communication constraints of randomly switching topologies and aperiodic communication pauses.
Remark 1 Less energy consumption is of great significance in practical engineer applications.The guaranteed-cost strategy aims to determine the upper bound of performance index, but it cannot ensure the energy consumption during the formation control process to be minimum, while the minimum-energy formation strategy is proposed to minimize the energy consumption by designing some optimization procedure.The formation control protocol (2) gives the formula of the total energy consumption, which is the sum of the quadratic integral function of energy consumptions of all followers.Thus, the relationship between the total energy consumptionEand the control gain matrixKis established.In addition, the control input of each agent is analyzed by interval, where each interval is divided into two subintervals; that is, the switching topology subinterval and the communication pause subinterval.In the switching topology subinterval,the control input of each follower comes from neighboring followers and the leader.In the communication pauses, no control input exists because there is no interaction channel among all the agents.
3.Minimum-energy leader-following formation design and analysis criteria
In this section, minimum-energy leader-following formation problems of the DMAS are studied, which is subjected to randomly switching topologies and aperiodic communication pauses.Firstly, the formation achievable problem is transformed into an asymptotic stability problem.Then, leader-following formation design criteria with the minimum-energy constraint are proposed in terms of the linear matrix inequality tool, which can be checked by the generalized eigenvalue approach.

Substituting (4) into (3) results in the following closedloop system:


which has the same eigenvalues as the similar matrixLσ(t).Because the matrixLˆσ(t)is symmetric and positive definite, there is at least one zero eigenvalue, then the

which means that the closed-loop system is decomposed into two subsystems that are determined byVz(t) andVz¯(t) , respectively.SinceUUˆσ(t)is nonsingular, it can be found from (15)-(17) thatVz(t) andVz¯(t) are linearly independent, which means that closed-loop system (5)can be decomposed into two subsystems.Due toit can be shown from (15) that
By (16), it can be found that
whereeiis theN-dimensional column vector with theith element being 1 and the other elements 0.By the structures ofVz(t), it can be ensured that

Thus, it means that the leader-following DMAS is formation achievable according to Definition 1.From the above analysis, it can be found that the macroscopically whole motion of all the followers is determined by subsystem (13); that is, the dynamics of the leader.The microcosmically relative motion of followers is depicted by subsystem (14).Based on the aforementioned derivation, it can be found that leader-following DMAS (1)with control protocol (2) is formation achievable if and only if subsystem (14) is asymptotically stable, which implies that the leader-following formation control problem is converted into an asymptotic stability problem.

In the following, minimum-energy leader-following formation design criteria of DMAS (1) with control protocol (2) is proposed in terms of the linear matrix inequality tool.


Proof Take common Lyapunov function candidates for subsystems (14) as

Let
then it can be proved by (22) and (25) that
Then, it can be found by (27) that
which indicates thatVi(t) is decreased in the switching topology subinterval [tp,t˜p).In the communication pause subinterval [t˜p,tp+1) (p∈N), differentiatingVi(t) along the trajectories of subsystems (14), it can be derived that
Let
then it can be shown from (22) and (29) that
Then, it immediately follows from (31) that

Combining (28) and (32) gives

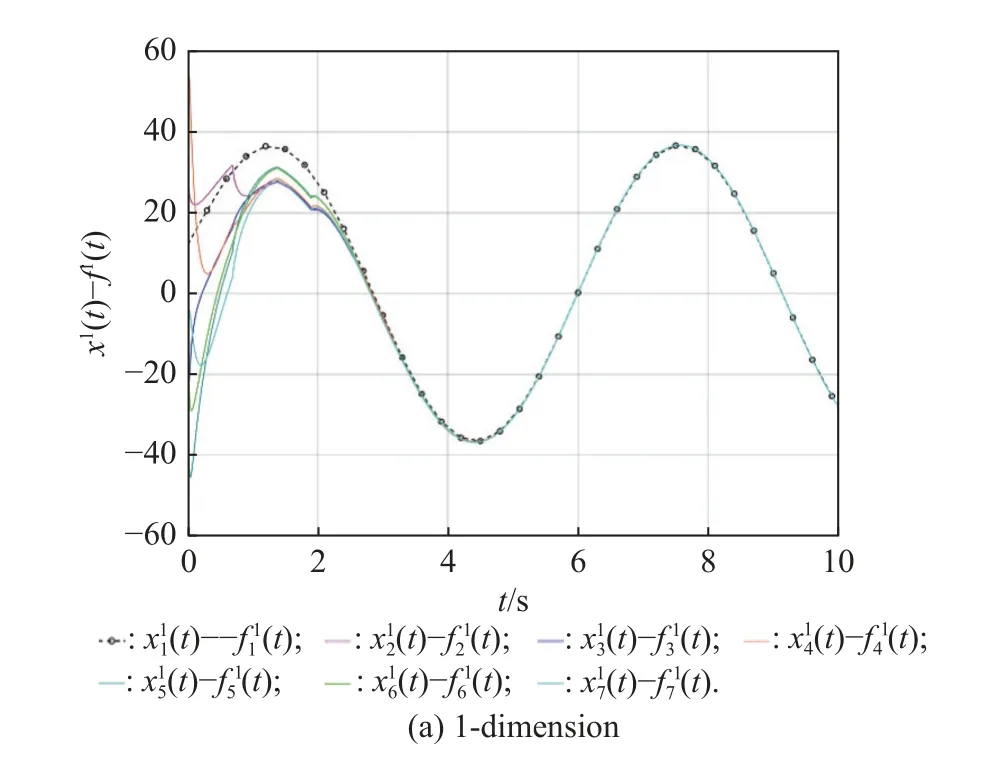
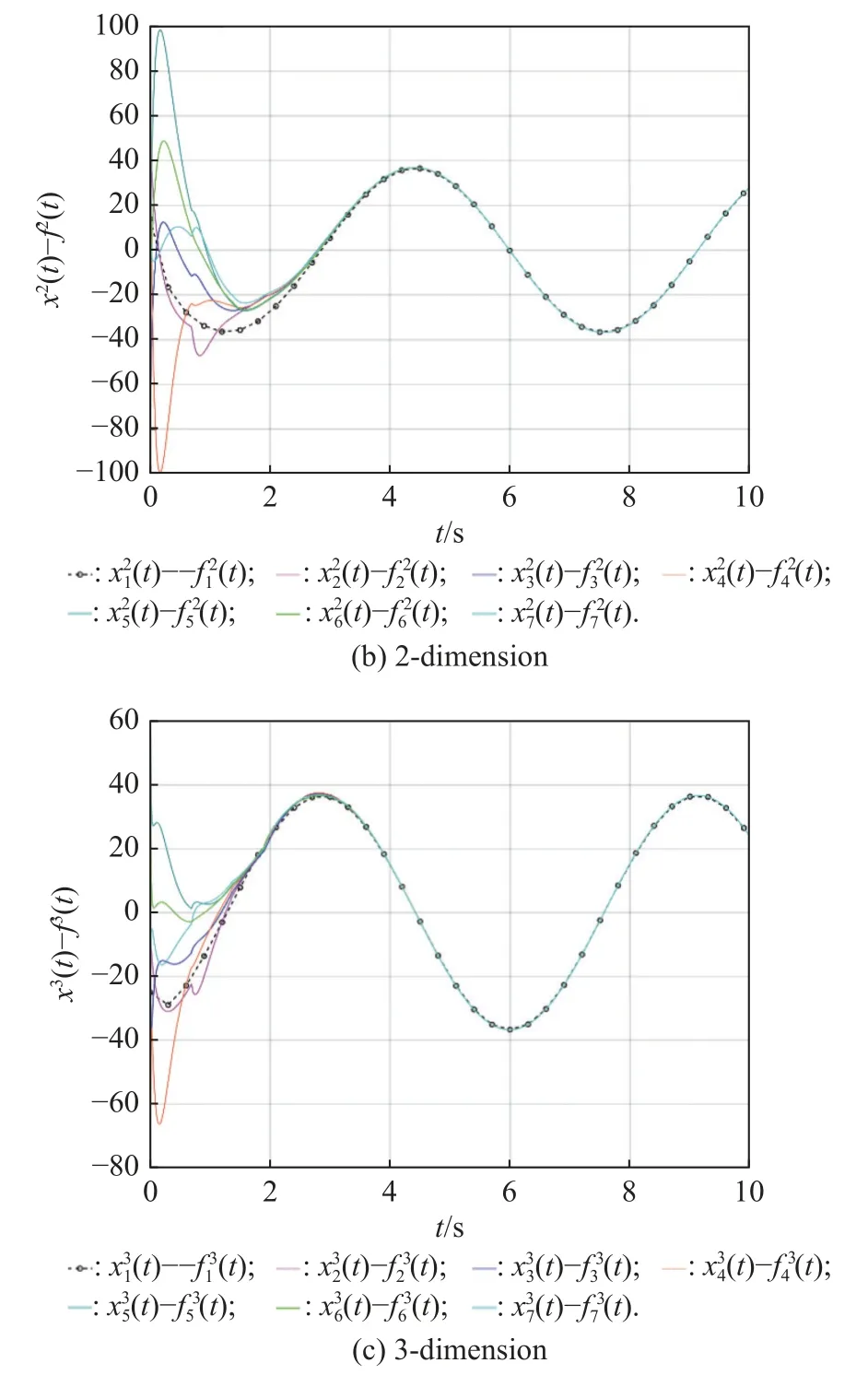
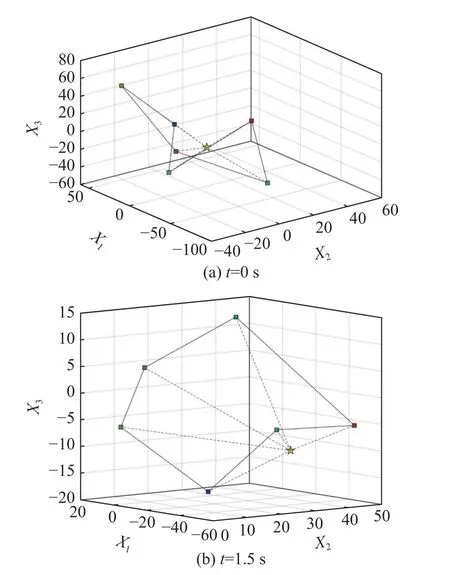
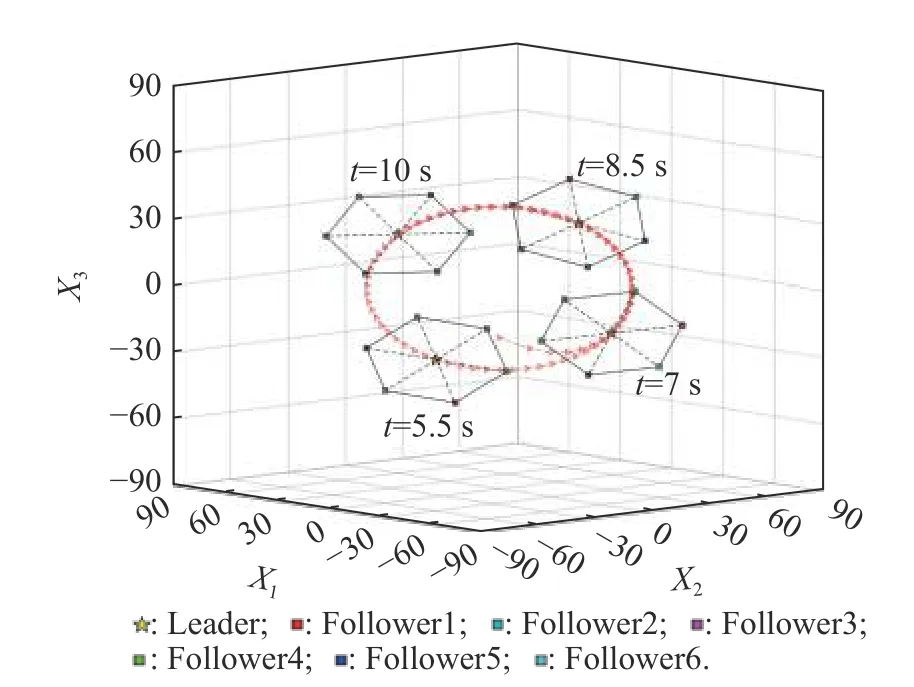
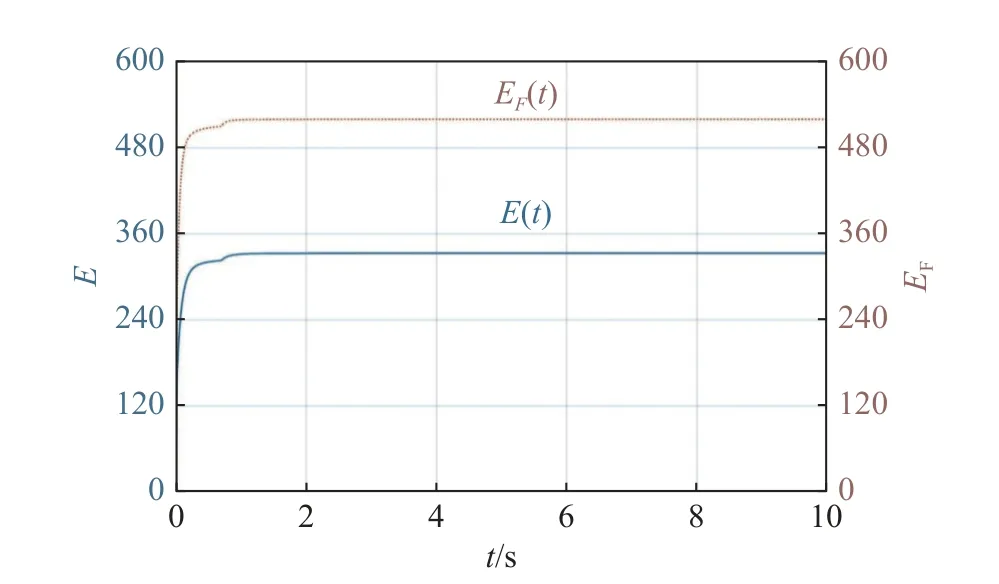
For any timetτ Due to τtmin≤t≤(τ+1)tmax, it can be derived that Substituting (38) into (37) yields Then, it can be derived that SinceHˆ is symmetric and positive definite, it can be deduced by (22) that By (14) and (42), one has According to the assumption of Definition 1, the initial conditions(i=2,3,···,N) are bounded and not all agreement.BecauseUis non-singular, there must exist somexˆi(0)≠0i∈{2,3, ···,N}, then the following inequality holds: Next, we can choose a positive scalar variable ℓ as the optimal parameter to construct the minimum-energy constraint as Due to it can be obtained that and Remark 5 In the actual situation, such as robots and unmanned aerial vehicles UAVs, there are different motion characteristics, dynamics and kinematics models,whose models containing the analysis of kinematics and dynamics can refer to [34].Actually, the dynamics of each agent in the DMAS can be modeled as a secondorder integrator with position and velocity states; i.e.,withxip(t) andxiv(t) representing the position-like state and the velocity-like state(see [35-37]).For example, the control of the UAV is usually decomposed into the position-loop control and the attitude-loop control.Note that the control of the attitude loop is realized by the internal controller of each agent and can be designed independently.However, the formation control of a DMAS belongs to the position loop,which means that the dynamics of each agent can be modeled as the second-order integrator.In this paper, the dynamics of each agent are modeled as general highorder ones, which contain second-order integrator cases.Hence, the dynamics model of each agent and the corresponding method in this paper can be used in the formation research for some practical multi-agent systems, such as robots and UAVs. Based on the aforementioned proofs, if the gain matrixKis given in advance, then sufficient conditions for minimum-energy leader-following formation achievement in the sense of linear matrix inequality is proposed below. In this section, a numerical simulation is provided to verify the above theoretical results.Consider a DMAS with agent 1 being the leader and agentsi(i=2,3,···,7) followers.The system matrices are The desired leader-following formation functions are set as follows: wherei=2,3,···,7. The switching set with four topologies is presented in Fig.1, where the yellow five-pointed star represents the leader and other different color squares denote six different followers.The switch signal of randomly switching topologies and aperiodic communication pauses is shown in Fig.2, where the time period is set ast=10 s and is divided by time intervals with 1.9 s, 2.2 s, 1.7 s, 2.3 s,and 1.9 s.In this case, the duration of each switching topology or each communication pause may be different,which means that the topologies are switched randomly and communication pauses are aperiodic with the maximum intervaltmax=2.3 s and the maximum communication pause rate ωˆ=0.35. Fig.1 Switching set Fig.2 Switching signal respectively.Then, the gain matrixKis Thus, the total energy consumption with the minimumenergy constraint during the time periodt=10 s isE(t)|t=10=331.310 9. It can be found that the total energy consumption with the minimum-energy constraint is less than the total energy consumption without the minimum-energy constraint int=10 s ; i.e.,E(t)|t=10 The tracking error trajectoriesxi(t)-fi(t)(i=1,2,···,7)in three different dimensions with the control gain matrixKare described in Fig.3, where the black curve with little circles depicts the trajectory of the leader.By Fig.3, it can be found that there are some little abrupt waves in the curve, which reflect switching actions from topologies to communication pauses, or switching actions among different topologies.It can be found that the desired formation can be achieved for the case that the topologies are switched randomly and communication pauses are aperiodic.Fig.4 exhibits position changes of the leader and six followers at the momentt=0 s, 1.5 s, 3.5 s, and 4 s, where the leader and six followers are marked by a yellow five-pointed star and six squares with different colors, respectively. Fig.3 Trajectories of xi(t)-fi(t) Fig.4 Position changes of the leader and six followers As shown in Fig.5, the leader rotates counterclockwise within 10 s, whose trajectory is shown by the red triangle dot line and is determined by the dynamics of the leader; that is,x˙1(t)=Ax1(t). Fig.5 Trajectory of the leader The curves ofE(t) andEF(t) are shown in Fig.6,where the two total energy consumptions trend to two different limited values.It can be found from Fig.6 that the total energy consumption with the minimum-energy constraint is less than the one with other methods during the leader-following formation process; i.e.,E(t) Fig.6 Energy consumption curves E(t) and EF(t) In addition, to show the difference of the simulation results with different values of parameters, the values of matricesA,B, the conversion coefficient α and the diffusion coefficient β are chosen as follows: it can be found that (A,B) is stabilizable, andf˙i(t)=Afi(t) and α(1- ωˆ)>β ωˆeβωˆtmaxare satisfied.With the other parameters being the same, the real symmetric matrixHˆ-1 of the Lyapunov function candidate and the minimum-energy optimal parameter ℓ are solved as respectively.Then, t he gain matrixKis In this case, the total energy consumption with the minimum-energy constraint during the time period isE(t)|t=10=75.311 2.From the above simulation results, it can be found that the different values ofA,B, α , and β may lead to the different gain matrix design, but the minimum-energy formation can be achieved by the associated gain matrix.Thus, it can be found that DMAS (1)with control protocol (2) can achieve the desired leaderfollowing time-varying formation with the minimumenergy constraint in the sense of the linear matrix inequality under the communication constraints of randomly switching topologies and aperiodic communication pauses. Minimum-energy time-varying formation problems of the leader-following DMAS subjected to randomly switching topologies and aperiodic communication pauses are addressed in this paper.Based on the proposed formation control protocol with the total energy consumption being involved, criteria of design and analysis for the minimumenergy formation are proposed, which can be checked by the generalized eigenvalue method.Especially, variables in criteria that are required to be solved are independent on the number of agents, which can guarantee the scalability of the DMAS.By a two-step transformation approach, the asymmetric Laplacian matrix of the leaderfollowing DMAS topology is well dealt with.Furthermore, the minimum-energy constraint can be determined,which is associated with the initial conditions and the relationship matrix, where the relationship matrix is the Laplacian matrix of the star graph with the interaction weight being one.In the further work, the minimumenergy leader-following formation control problems with jointly spanning tree topologies will be further researched.
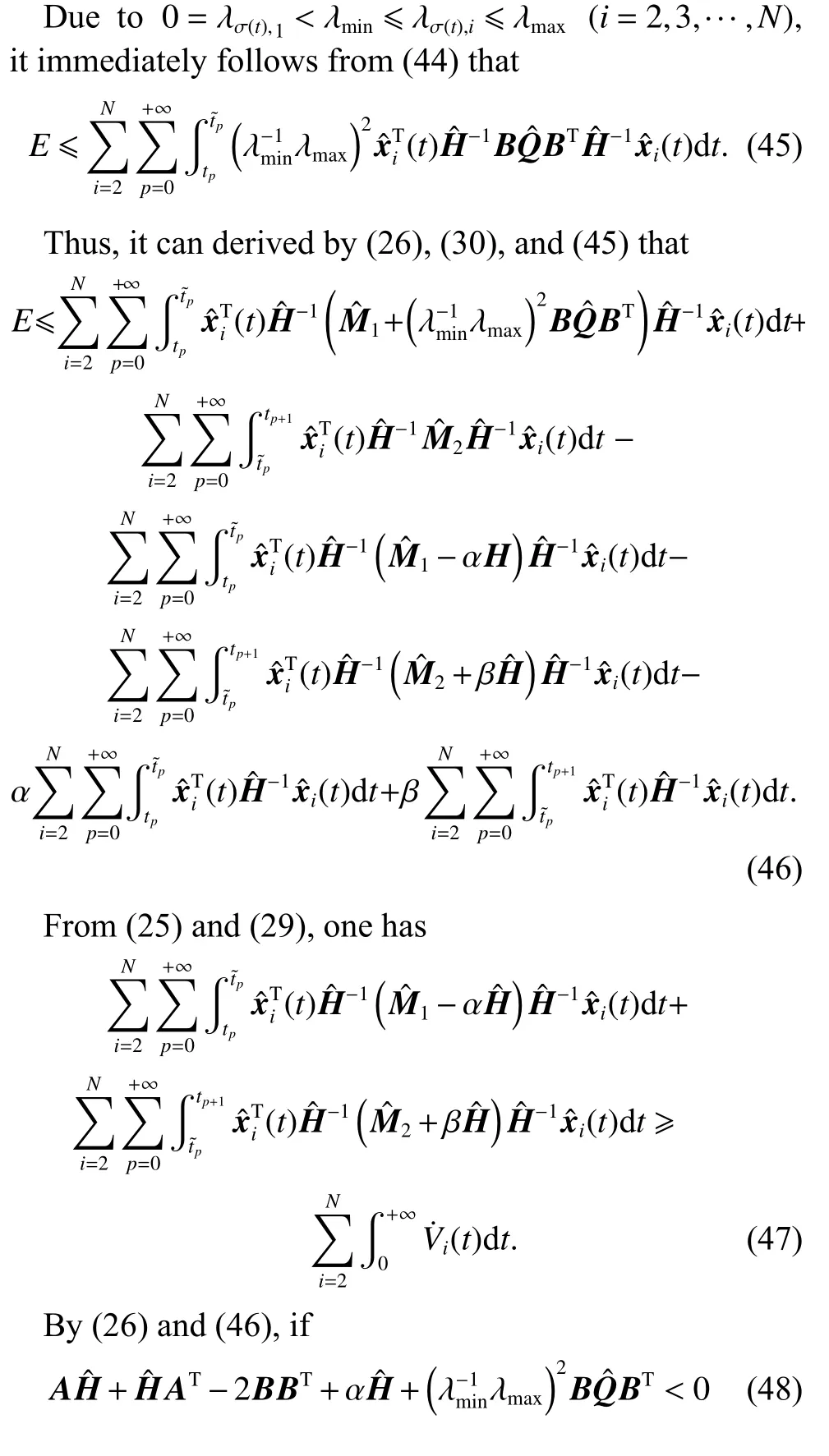





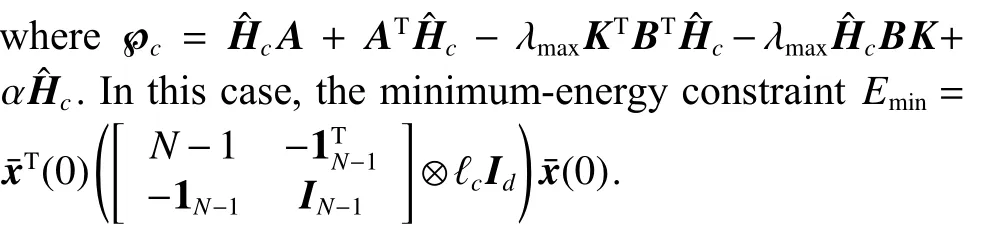
4.Numerical simulations



5.Conclusions
杂志排行
Journal of Systems Engineering and Electronics的其它文章
- Support vector regression-based operational effectiveness evaluation approach to reconnaissance satellite system
- K-DSA for the multiple traveling salesman problem
- Uncertainty entropy-based exploratory evaluation method and its applications on missile effectiveness evaluation
- Formal management-specifying approach for model-based safety assessment
- Consensus model of social network group decision-making based on trust relationship among experts and expert reliability
- A cooperative detection game: UAV swarm vs.one fast intruder
