Two-layer formation-containment fault-tolerant control of fixed-wing UAV swarm for dynamic target tracking

QIN Boyu, ZHANG Dong,*, TANG Shuo, and XU Yang

1.School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2.Shaanxi Aerospace Flight Vehicle Design Key Laboratory, Xi’an 710072, China; 3.School of Civil Aviation, Northwestern Polytechnical University, Xi’an 710072, China

Abstract: This paper tackles the formation-containment control problem of fixed-wing unmanned aerial vehicle (UAV) swarm with model uncertainties for dynamic target tracking in three-dimensional space in the faulty case of UAVs ’ actuator and sensor.The fixed-wing UAV swarm under consideration is organized as a “multi-leader-multi-follower” structure, in which only several leaders can obtain the dynamic target information while others only receive the neighbors’ information through the communication network.To simultaneously realize the formation, containment, and dynamic target tracking, a two-layer control framework is adopted to decouple the problem into two subproblems:reference trajectory generation and trajectory tracking.In the upper layer, a distributed finite-time estimator (DFTE) is proposed to generate each UAV ’s reference trajectory in accordance with the control objective.Subsequently, a distributed composite robust fault-tolerant trajectory tracking controller is developed in the lower layer, where a novel adaptive extended super-twisting (AESTW) algorithm with a finite-time extended state observer (FTESO) is involved in solving the robust trajectory tracking control problem under model uncertainties, actuator, and sensor faults.The proposed controller simultaneously guarantees rapidness and enhances the system ’s robustness with fewer chattering effects.Finally, corresponding simulations are carried out to demonstrate the effectiveness and competitiveness of the proposed two-layer fault-tolerant cooperative control scheme.

Keywords: fixed-wing unmanned aerial vehicle (UAV) swarm,two-layer control, formation-containment, dynamic target tracking.

1.Introduction

With the recent advancements in computing, communication, sensing, and control techniques, the research on unmanned systems in many fields (such as aerospace,marine, and earth science) has become a hot spot and gradually steps into the realistic application [1-4].In particular, cooperative control of the unmanned aerial vehicle (UAV) swarm system has gained widespread attention by virtue of its potential value in complex and dangerous tasks such as battlefield reconnaissance-attack scenarios, disaster monitoring, and power grid inspection,as well as the efficiency and robustness of task execution[5-9].As a cooperative control mode that only relies on the local state information of the system, distributed control has been favored by researchers for its advantages of significantly reducing communication costs and effectively enhancing communication robustness.According to the number of leaders in the unmanned systems swarm,distributed control problems can be classified into the following three categories: the leaderless consensus and formation control [10], the “single-leader-single-follower”tracking control [11], and the “multi-leader-multi-follower” containment control [12].Most cooperative control problems can be abstracted into the combination of the three basic control problems mentioned above.

To incorporate the aforementioned merits of distributed control into UAV swarm, a series of researches focusing on some typical application scenarios have been carried out with various control strategies proposed[13-18].It is worth mentioning that most results like[14-18] are concerning cooperative control of UAV swarm with either fully distributed or “single-leadermulti-follower” structures.Nevertheless, with respect to cooperative control for UAV swarm with “multi-leadermulti-follower” structure, the attention is still less.

In fact, due to stronger robustness and more diversified task abilities, “multi-leader-multi-follower” structure is more practical in the applications, especially for the swarm consisting of individuals with heterogeneous task capabilities like detection and attack to cooperatively execute different tasks of a target.Recently, some researchers have gradually noticed the significance of control for “multi-leader-multi-follower ” swarm, and have made some contributions to a coordination scenario,namely “formation-containment” control.However, there still exist limitations mainly reflected in two aspects.First, the agent in the research is usually a theoretical system with highly-abstract mathematical model (like integrator system, high-order linear system) and the proposed controller cannot be directly adopted in the real unmanned systems with more specific and complex dynamics under various uncertainties, faults and disturbances.Second, the swarm is usually desired to keep at fixed points or track a static target.For example, in[19-21], the swarm macroscopic motion was unable to be controlled to track the time-varying reference or maneuvering target.

Up to now, to the best of our knowledge, the attention concerning formation-containment control of fixed-wing UAVs for dynamic target tracking is hitherto rare.It is the primary motivation to develop a practical formationcontainment control framework for “multi-leader-multifollower” fixed-wing UAV swarm system with complex flight dynamics to track dynamic target.

Furthermore, due to the model errors and the possible aging or sticking of mounts of actuators and sensors,uncertainties and faults are the challenges that need to be solved in the fixed-wing UAV control process, which places a high demand on the fault-tolerance and robustness of the UAV controller.This demand becomes more significant when it comes to the UAV swarm system because the negative impacts of the faults on one UAV flight states may be transmitted to others through the communication network.In that way, the negative effects will be amplified with “the Butterfly Effect” induced, and lead to the swarm’s performance degradation or even instability [22].It is therefore meaningful and necessary to propose a control framework of the fixed-wing UAV swarm to simultaneously achieve the formation-containment control for dynamic target tracking and suppress influence of the unknown uncertainties and faults to maintain the performance.

As a key control technique to enhance system robustness and safety against faults and uncertainties, fault-tolerant control (FTC) was widely investigated and applied in many fields [23-25] like electricity generation and wind turbines [26-30].The application of FTC to cooperative control of multi-UAV/UAV swarm systems,namely fault-tolerant cooperative control (FTCC),became a current hot spot [31-34].Some FTCC works about the UAV swarm’s attitude coordination [35,36],“single-leader-multi-follower ” swarm consensus [37],and the UAV formation on the two-dimensional (2D)plane [38] were reported, inspiring to further promote the research on FTCC from both new scenarios and novel approaches.Despite the above outstanding works, how to design the FTCC for the “multi-leader-multi-follower”fixed-wing UAV swarm system to achieve formationcontainment control for dynamic target tracking in threedimensional (3D) space is still a currently unsolved problem.Motivated by the above concerns, this paper intends to address the formation-containment FTC problem of fixed-wing UAV swarm for dynamic target tracking under the model uncertainties, actuator and sensor faults.Compared with the previous literature, this paper contains the following novel features and contributions:

(i) Most existing coordination control of multi-UAV or UAV swarm systems focuses on single-task or dual-task problems (e.g., formation or containment or their combination), which are inappropriate to simultaneously cope with threefold-task problems of formation, containment and dynamic target tracking.Additionally, formationcontainment control methods presented in [19-21] are not directly applicable to our case, due to the inherent characteristics of fixed-wing UAV in 3D space.

(ii) In contrast to [5,6,17,39], a novel control-oriented UAV dynamics model in 3D space in the sensor and actuator faulty case is constructed with low-speed aerodynamics and uncertainties of thrust and aerodynamics,which makes the dynamics model more precise to describe the UAV real flight process and more practical for the cooperative controller design.

(iii) In the upper layer, a novel distributed finite-time state estimator (DFTE) is designed for leaders and followers to generate the reference trajectory satisfying the objectives of formation, containment and dynamic target tracking under the circumstance of only several leaders capable of the dynamic target’s position and velocity.The designed estimator extends the time adjustable range, and the generated trajectories are much more continuous and smoother compared with [40-42].The proposed DFTE is therefore more general and practical.

(iv) In the lower layer, a distributed composite robust fault-tolerant trajectory tracking control strategy is developed based on a novel control-oriented UAV dynamics model constructed in 3D space.The nonlinearity induced by model uncertainties and faults are addressed by a novel proposed “adaptive extended super-twisting algorithm” (AESTW) incorporating integral terminal sliding modes and a finite-time extended state observer(FTESO).Compared with the two commonly-used highorder sliding mode control approaches: conventional super-twisting algorithm in [43] and the fast super-twisting algorithm in [44], the proposed AESTW can sufficiently lessen the chattering effects with robustness and finite-time convergence guaranteed and the signals varies much smoother and continuously, which is meaningful for lower requirements on the signal switching speed of UAV controller in the real application.

2.Preliminaries

2.1 Key notations

Some key notations of the paper are shown in Table 1.

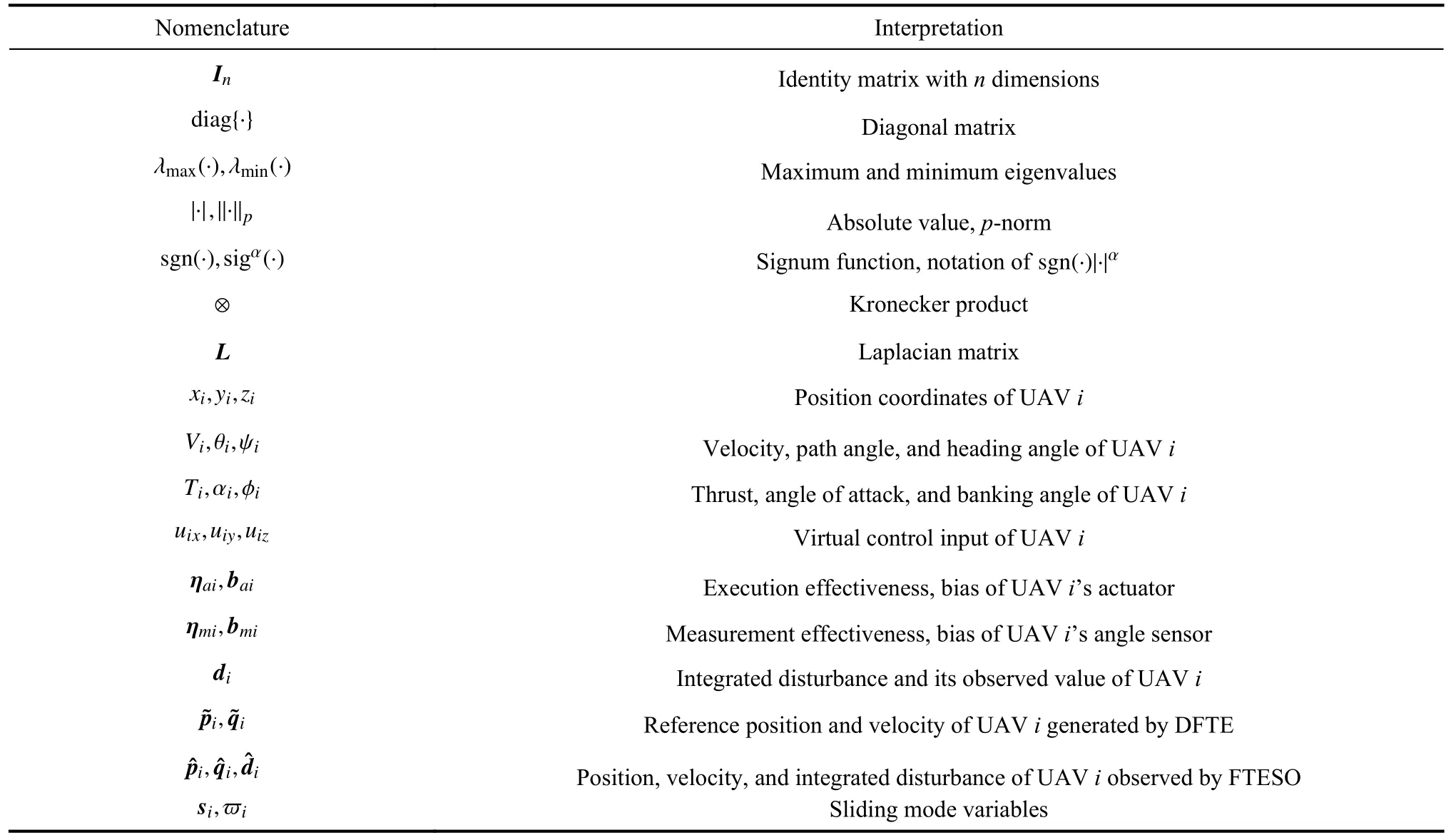
Table 1 Some key notations

2.2 Fixed-wing UAV model

The dynamics variables are shown in Fig.1.

Fig.1 Coordinate system and dynamics variables

In the following sections of this paper, the model assumes that the autopilot can stabilize the UAV attitude and the slide angle is zero.It is also assumed that the earth is flat and the fuel expenditure is negligible.Under these assumptions, the 3-DOF dynamics model can be described by

For the low-speed fixed-wing UAVi, the nominal models of liftLiand dragDi[45] are respectively

whereVmiis the mean wind speed relevant to the heightyi.The wind gust turbulenceVmi,tanis assumed to a Gaussian random variable with zero mean and a standard deviation of 0.09Vmi.

2.3 Actuator and sensor fault models

In the UAV swarm cooperative control, the actuator and sensor faults may significantly degrade the control performance or even cause system crashes.To improve flight safety, the actuator and sensor faults should be explicitly considered.Inspired by [47,48], the actuator faults consisting of the loss of execution effectiveness and fault bias can be denoted as

The measured signals of the track angle and heading angle used by the controller deviate from the true signals by considering factors such as loss of measurement validity and measurement bias error of the angle sensor.The sensor fault model of UAViis

2.4 Model transformation

In general, the angle of attack αiof UAViduring the flight is so small that cosαi≈1 and sinαi≈αi, and si multaneously the thrust termTisinαicanbe neglected since itisfarsmaller than liftLi[49].Meanwhile,only the lineartermsof dragconcerning theangleofattackαiare retained, andthe higher-orderterms are treated as perturbations.By substituting (4), (6), and (7) into (2), one can render that

From (1), (2), and (6)-(9), the control-oriented UAV model with actuator and sensor faults can be obtained as follows:

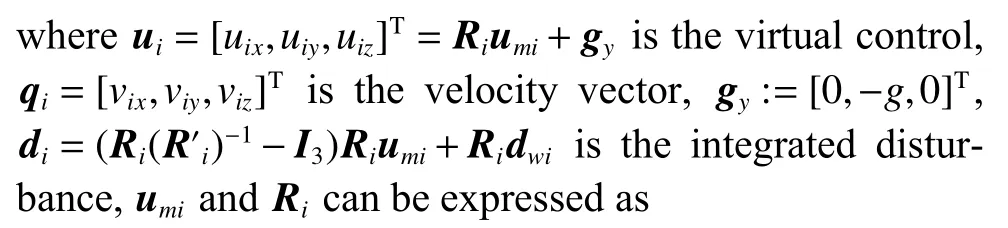
According to (10)-(12), the mathematical relation between the virtual control vectoruiand the real control input vector µi0=[Ti0,αi0,ϕi0]Tis

Assumption 1 For the dynamics system as (10), the integ

rated disturbancedi(t) is continuously bounded and differentiable.Its derivative

Remark 1 Assumption 1 is a common assumption in the research of disturbance-observer based control.In the application, the integrated disturbance caused by many real physical processes meets this assumption.For example, the actuators and sensor efficiency may gradually decrease in a period of time and keep at a constant level at the end, and the bias of actuators and sensors may keep a constant.In these scenarios, the derivatives of disturbances are generally bounded.

2.5 Graph theory

Assumption 2 The topology among the target and leader UAVs contains at least one directed spanning tree,the root node of which is the target.

Assumption 3 For each follower UAV, there exists at least a directed path from one of the leader UAVs, the information interactions in both the leader layer and the follower layer are bi-directional.

Remark 2 Assumption 2 and Assumption 3 are common assumptions in the research of formation-containment control.In the application, the hierarchical architecture with multi-leader-multi-follower is a common one when it comes to some scenarios with different agents executing multiple tasks.For example, in the escort missions, the outboard UAVs in the swarm can serve as the leaders to get the target states and guide the whole swarm’s movement, while the inner UAVs only need to follow the leaders.By the fore-end process of UAV swarm communication construction, the swarm topology assumptions can be met.

Let Assumption2andAssumption3hold, thestructur edivisionof theLaplacianmatrixL∈RN×Nof the UAV swarm is described as

whereL0l∈RNl×1indicates the leaders’ access to the information of the target,Lll∈RNl×Nlrepresents the interaction among the leaders,Ll f∈RNf×Nlrepresents the communication from the leaders to the followers, andLl f∈RNf×Nlmeans the interaction among the followers.

2.6 Control objective

The control objective is to achieve the UAV swarm formation-containment control for the dynamic target tracking in the actuator and sensor faulty case.

For the UAV swarm composed of the leader layer and follower layer, the formation-containment control for tracking the dynamic target is said to be achieved when the following conditions are simultaneously met: (i) the leaders form a desired time-varying formation; (ii) the followers converge into the convex hull of leaders; (iii) the whole swarm tracks the dynamic target.The definitions can be described as follows.

wherep0(t) represents the position of the mobile target,pi(t) is the position of UAVi, andhi(t) is denoted as the leader’s desired time-varying formation function, which is piecewise continuously differentiable.

According to the analysis for control objectives of different layers, the control framework is designed as illustrated in Fig.2.

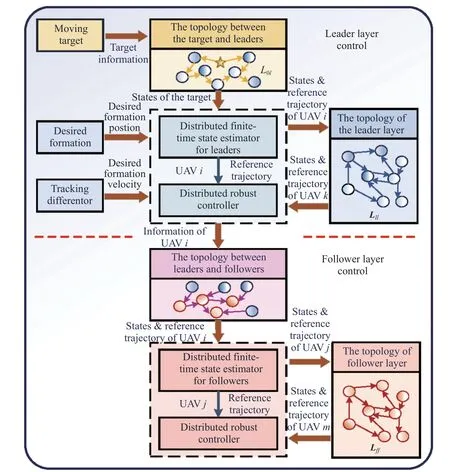
Fig.2 Hierarchical cooperative control framework

2.7 Lemmas

Lemma 1 [52] Under Assumption 2 and Assump-

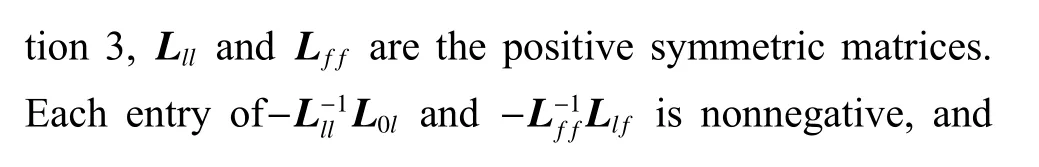
3.Main results

In this section, DFTE is first developed for each UAV to generate the reference trajectories.Then, FTESO is adopted to diagnose the integrated disturbances.In addition, Nonlinear integral terminal sliding mode (NITSM) is designed with the AESTW algorithm proposed to significantly enhance the robustness and effectively weaken the chattering effects.The control architecture is shown in Fig.3.

Fig.3 Structure of the control scheme

3.1 Distributed finite-time estimator

To enable each UAV to online generate the desired trajectory which satisfies the requirements of control objectives, DFTE is designed.Most of the existing distributed state estimators [40-42] adopt sliding mode control(SMC) based on the sign function with discontinuous value, which is sensitive to signal changes and induces the obvious chattering effect.

Considering the above problems, non-smooth functions are introduced to design DFTE to weaken the chattering effect and simultaneously guarantee the robustness and finite-time convergence characteristics.

For the leader UAVi, the distributed finite-time estimator is designed as

Remark 3 Assumption 4 is a common assumption in the relevant research.In the real scenario, due to the constraints of the kinematics and maneuvering ability, the target’s velocity and the acceleration are always bounded.Also, the desired formation function and its derivative can be always designed as continuous or smooth functions manually based on tasks.Thus, the assumption is reasonable.

Theorem 1 Using the estimators noted by (16), each leader can individually estimate the desired position and velocity in a finite timeT2for the formation tracking,which can be expressed as

yielding that

For follower UAVs, the distributed finite-time estimator is proposed as follows:

where σ0,m3,m4are constants, and σ0∈(0,1) andm3,m4>0.

Theorem 2 Using the estimators noted by (22), each follower can individually estimate the desired position and velocity in a finite timeT4for the containment, which can be expressed as

3.2 FTESO

The FTESO proposed in [55] is applied to the diagnosis and compensation of the integrated disturbance caused by faults and model uncertainties.Regard the integrated disturbancedias the extended state of the system (10), and the observer is described as

Remark 5 Here it needs clarifying the FTESO and DFTE.Both of them can be called estimators and observers, but there is a functional difference between them.DFTEs designed in Subsection 3.1 are applied to distributed generating each UAV’s reference trajectory based on the neighbor’s information for the leaders’ formation, the followers’ containment, and the whole swarm tracking dynamic target.In contrast, FTESOs in this subsection are used for each UAV to observe and compensate the integrated disturbance, alleviating the negative effects of faults and model uncertainties on UAV swarm flight.

3.3 Distributed adaptive NITSM control

To further enhance the robustness of the control system,NITSM is designed and the AESTW algorithm is simultaneously proposed to track the reference trajectories generated by DFTE so that the system robustness significantly improves while the convergence speed is guaranteed.

The NITSM surfacesi= [si1,si2,si3]Tis designed as

whereueq,i= [ueq,i1,ueq,i2,ueq,i3]Trepresents the equal input.Apparently,si(0) = 03whent= 0, which means that the states of UAViare located on the sliding mode surface(25) at the initial time.The equal controlueq,iguarantees states of UAViconverge along the sliding mode surfacesi= 03in a finite time.ueq,iis defined as

where0<β1<1 , β2=2β1/(β1+1),l3,l4>0.q˙˜ican be obtained by the tracking differentiator in [56].

The AESTW algorithm is designed with sliding-mode switching control inputusw,ias

where 0.5<σ1<1 , and σ2=2σ1-1.l1andl2are adaptive gains, and correspondingly the adaptive law is

where ε>1/σ1,w1,υ1,χ>0.∆s>0 and its value is relevanttoparametersw1, υ1, χ,andthedisturbance amplitudeδ,whichcanbe adjusted according tothe control accuracy.

Taken together, the adaptive NITSM robust control protocol is designed as

Theorem 3 Under the control protocol (30), the UAV swarm (10) with the communication topologyGcan track the reference trajectories generated by DFTE and achieve the formation-containment control for tracking the dynamic target.

Proof The proof can be divided in two steps:(i) UAVican approach and then keep on the slidingmode surfacesi= 03; (ii) Whensi= 03, UAVican track the estimated statesp˜iandq˜iin a finite time.For the first step, the derivative of the NITSM (25) is

4.Simulations and analyses

4.1 Description of simulation scenarios

A topology G of the UAV swarm composing of eight leader UAVs (Numbered from 1 to 8) and four follower UAVs (Numbered from 9 to 12) are shown in Fig.4.It can be proved that the topology is satisfied with Assumption 2 and Assumption 3.The model parameters of each UAV are shown in Table 2.Also, consider that the real input has saturation limits with 0 N ≤Ti≤25 N,-12◦≤αi≤12◦, and -60◦≤ ϕi≤60◦.

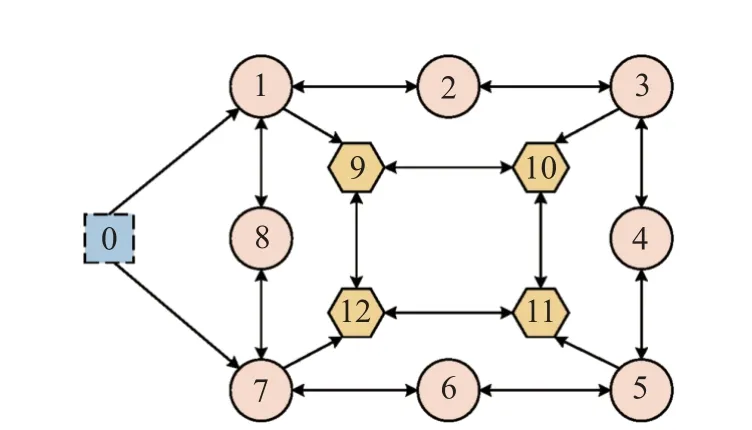
Fig.4 Topology of the UAV swarm

Table 2 Model parameters of each UAV

At the initial time the scalar velocityViof each UAV is 20 m/s, and the path angleθi(0) and the heading angleψi(0) are all zero.The initial positions of UAVs are randomly generated, chosen as:p1(0) = [-151 m,11 m,1 747 m]T,p2(0) = [-1 271 m,11 m,1 677 m]T,p3(0) =[-1 216 m,24 m,830 m]T,p4(0) = [-509 m,27 m,957 m]T,p5(0) = [-371 m,24 m,1 485 m]T,p6(0) = [-920 m,29 m,1 482 m]T,p7(0) = [-1 148 m,29 m,865 m]T,p8(0) =[-478 m,30 m,1 184 m]T,p9(0) = [-915 m,23 m,1 329 m]T,p10(0) = [-528 m,11 m,1 141 m]T,p11(0) =[-628 m,22 m,1 498 m]T, andp12(0) = [-923 m,17 m,1 359 m]T.The mean wind speedVmat the altitude of 80 m is 4 m/s.

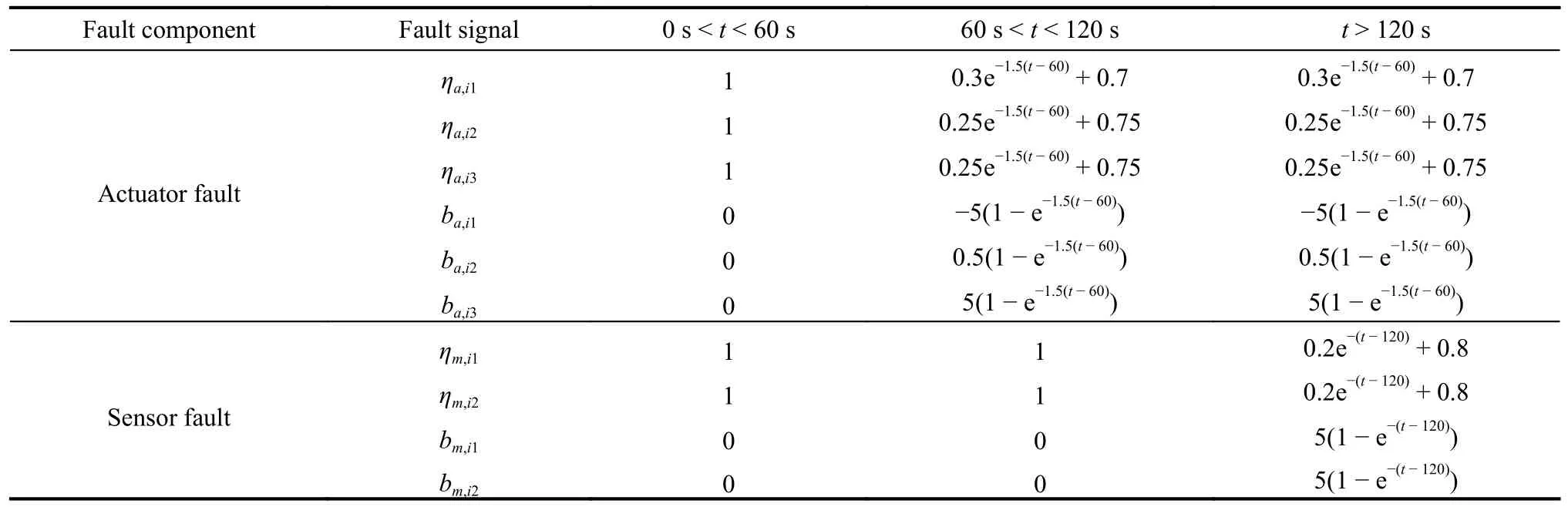
Table 3 Fault signals encountered by each fixed-wing UAV (°)

The parameters for the control scheme of each UAV are chosen that: (i) for the DFTE,σ0= 0.5,m1= 3.5, andm2= 2.5; (ii) for the FTESO,κ= 0.5,k1= 18,k2= 108,andk3= 216; (iii) for the NITSM,β1= 0.6,β2= 2β1/(β1+1) = 0.75,l3= 0.6, andl4= 3; (iv) for the AESTW,σ1=0.5, andσ2= 2σ1- 1 = 0.4; (v) for the adaptive law,l1(0) =5,w1= 5,υ1= 2,χ= 0.5,ε= 4 /σ1= 5.71, andΔs= 10-3.

In the simulations, two scenarios are selected to present the effectiveness of the control scheme for tracking targets of different maneuver types, including: (i) The planar formation tracks the target in cycloid motion on the 2D ground; (ii) The cubic formation tracks the spiral climbing target in 3D space.The time-varying position and velocity of the mobile target and the desired formation function of leader UAVs under the two scenarios are shown in Table 4 respectively.

4.2 Effectiveness verification

In this subsection, the effectiveness of the proposed cooperative control scheme is first verified by simulations of the two scenarios above.The UAV trajectories of two scenarios are shown in Fig.5.

Fig.5 Trajectory of each UAV in the two scenarios

In Fig.5(a) and Fig.5(b), the dynamic targets are marked by the purple pentagon.The black hexagrams represent the leader UAVs, while each follower is described by a red triangle.The black markers in Fig.5(a) indicate the projection of each UAV on the ground.Apparently, whether the planar formation tracks the target cycloidally moving on the ground or the cubic formation tracks the target spirally climbing in the 3D space, both layers of the UAV swarm can achieve the control objectives.

Without loss of generality, the following content mainly presents the simulation results and analyses of the cubic formation scenario.For the cubic formation swarm,the status of the followers and the leader att= 40 s, 80 s,120 s, 160 s are given.Obviously, all UAVs are scattered at the initial time, and the expected formation, containment tracking are not quite achieved att= 40 s.Then,fromt= 40 s to 80 s, all the leaders almost realize a stable time-varying cubic formation with all the followers in the convex hull all the time.After that, the states of each UAV converge further so that one can obtain higher accuracy.tracking error starts converging extremely small since aroundt= 120 s.

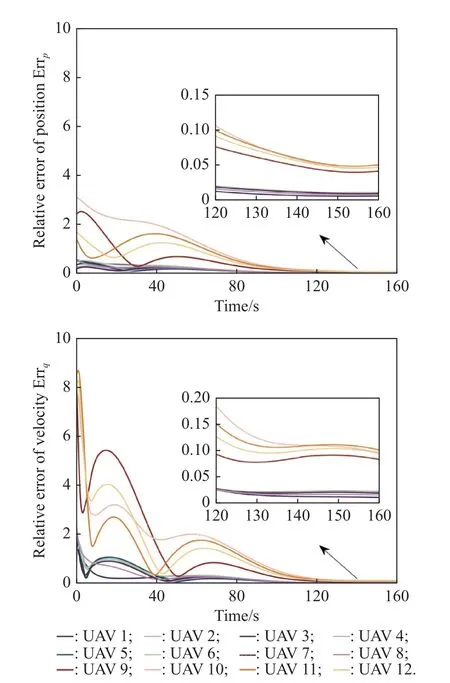
Fig.6 Relative error of position and velocity tracking

The variation of each UAV’s dynamics parameters and control inputs with time are given in Fig.7-Fig.9,respectively.

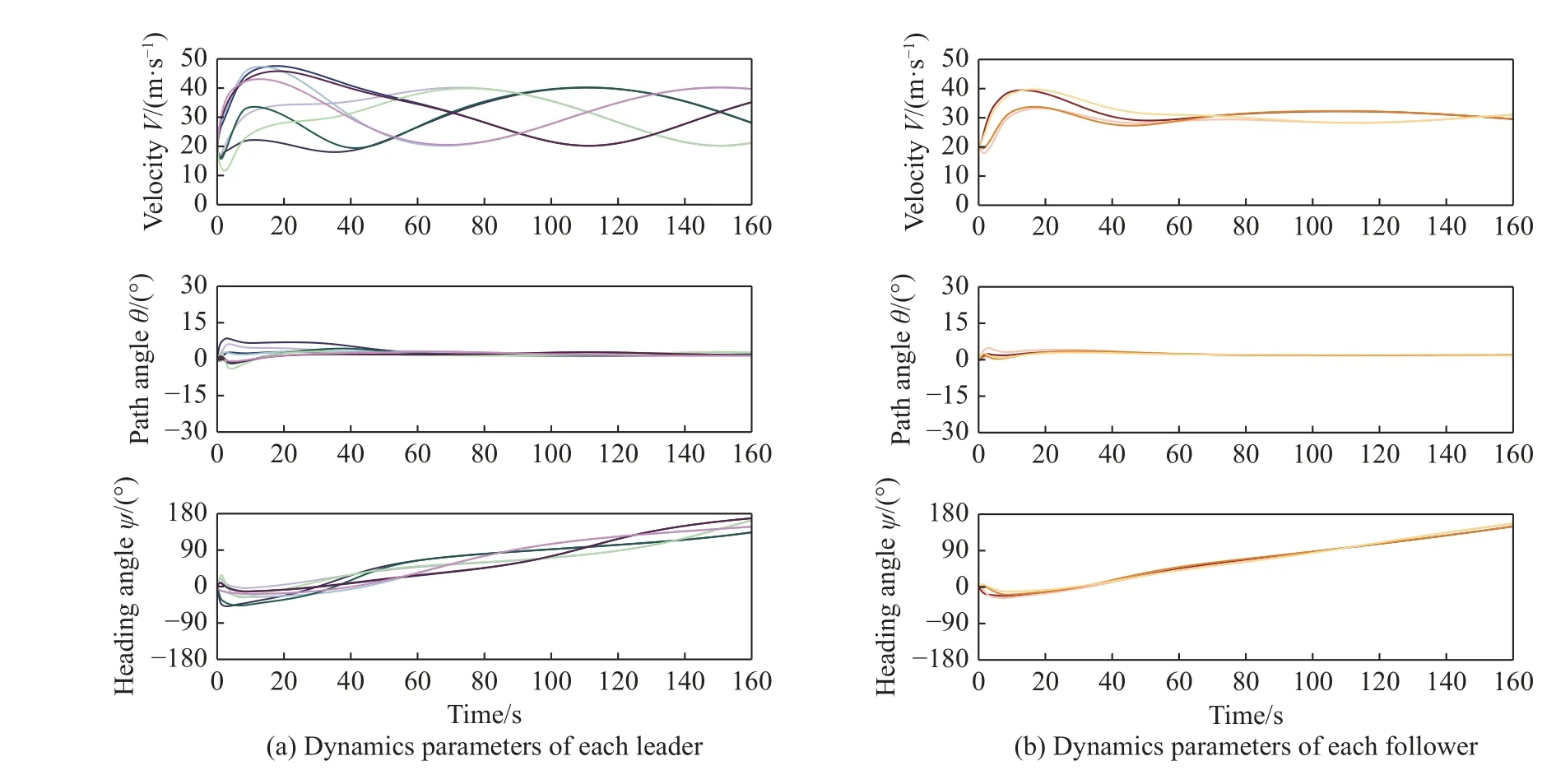
Fig.7 Variation of dynamics parameters and control input of each UAV

It is clear that with the proposed cooperative control protocol, the fixed-wing UAV swarm is able to achieve formation, containment and tracking the dynamic target under the time-varying disturbances, actuator and sensor faults, and both layers can realize their control objectives with steady dynamic transient processes.

Further, to demonstrate the effectiveness of the proposed control protocol in diagnosing disturbances, Fig.8 shows the disturbance observation error of FTESO for each UAV.Obviously, one can see that FTESO can achieve convergence quickly and the integrated disturbances, which are composed of model uncertainties and faults, are perfectly estimated by the FTESO.

Fig.8 Disturbance estimate error

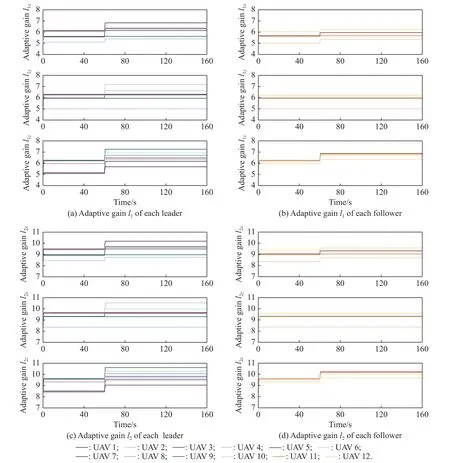
Fig.9 Adaptive gains of AESTW for each UAV

Fig.11 shows the convergence process of the gains of the AESTW algorithm for each UAV, which verifies the effectiveness of the adaptive law.

To further illustrate the influence of different parameters on the control performance and guide the parameter selection, the simulations for DFTE and AESTW are carried out with different parameters selecting different values.Fig.12 and Fig.13 show the variation of DFTE estimate error with different σ0,m1,m2, and AESTW sliding modes with different σ1, respectively.

For σ0in the DFTE, according to the results in Fig.10, when σ0increases from 0 to 1, chattering effects will be gradually weakened and the signals vary smoothly.Nevertheless, according to Theorem 1 and Theorem 2, as σ0approaches 1, the estimate errorsepi,evicaused by the desired time-varying formation function and target’s unknown maneuvering will increase,making the upper boundness of the estimate errors,i.e., the trajectory estimation precision degraded.Thus,by adjusting σ0, a trade-off between weakening chatter effects and guaranteeing the control precision and convergence time can be achieved.Based on the simulation results, when the value of σ0is selected in [0.25,0.50], chattering effects can be significantly alleviated and the estimate errors can be guaranteed small at the same time.

Fig.10 Estimate error variation varying with σ0

For σ1∈(0.5,1),σ2=2σ1-1 in the AESTW, according to the results in Fig.11, when σ1increases from 0.5 to 1, chattering effects will be gradually weakened and the sliding mode variables vary smoothly.However,according to the proof and analysis in Theorem 3, when σ1approaches 1 (like σ1is selected as 0.90 or 0.95), the signal may oscillate in a small range due to the disturbance.Based on the above results, it is better to selectσ1in [0.60, 0.80] to both weaken chattering effects and guarantee the anti-disturbance ability.

Fig.11 UAV 1’s x-orientation sliding mode variation varying with σ1

To illustrate the proposed controller has antisaturation ability, here a simulation is carried out under the actuator saturation.To show the controller performance under the saturation more clearly, here the saturation limits can be further narrowed as the 80% of the original ranges, i.e., 0 N ≤Ti≤20 N,-9.6◦≤αi≤9.6◦, and -48◦≤ϕi≤48◦.Under these real input limits, the thrustTi, angle of attack αiand banking angle ϕiin the simulation are shown in Fig.12.

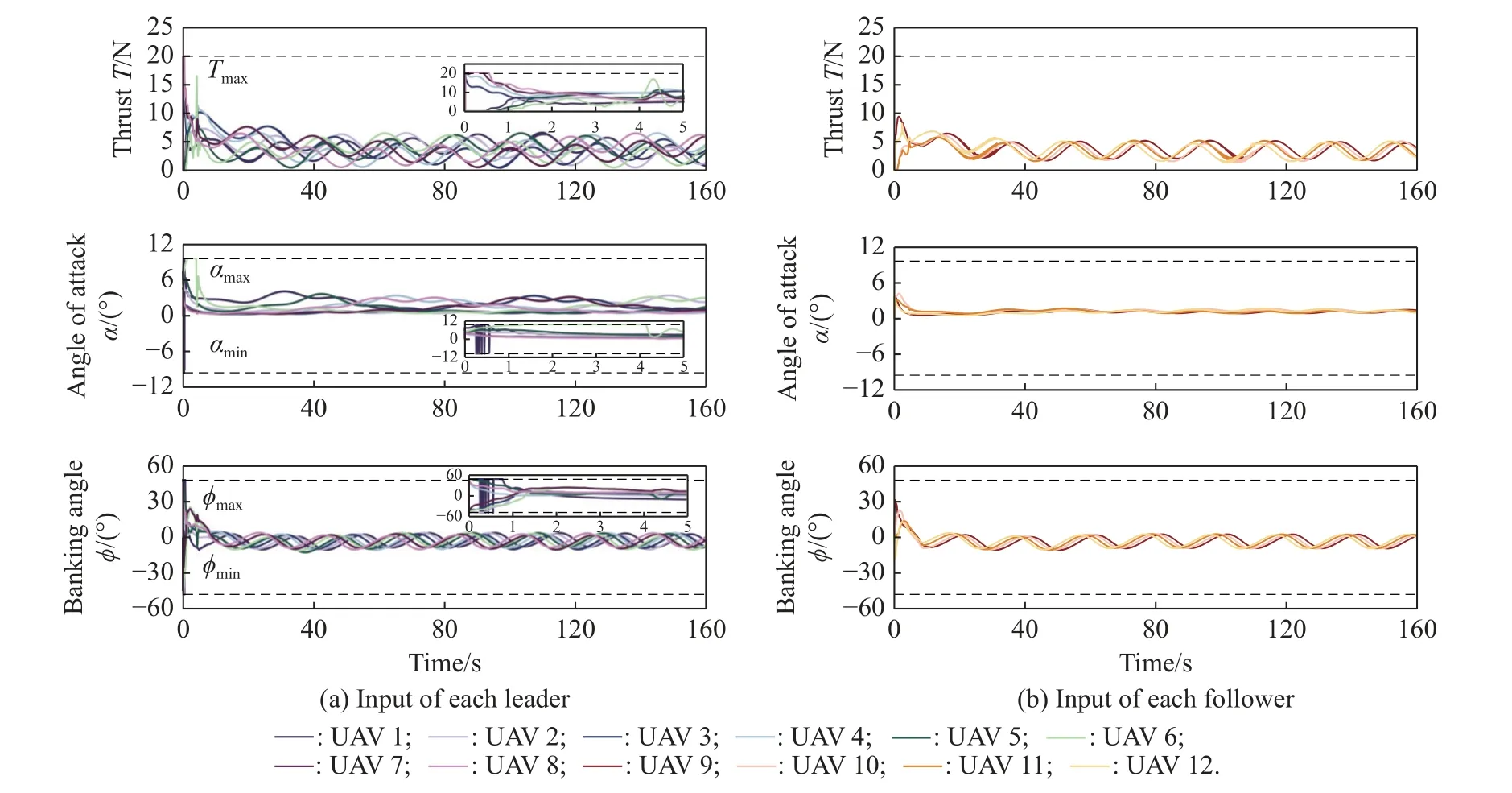
Fig.12 Input of each UAV with saturation limits

From the simulation results, it can be seen that the thrust, angle of attack and banking angle saturation occurs at the beginning period (about 0-5 s), especially for UAV 6, of which the thrust saturation continues for about 4 s.However, the controller can still work under the control input saturation, which shows the anti-saturation ability of the designed controller.

4.3 Comparison with the existing work

In this subsection, the same problems of formationcontainment control for tracking the dynamic target are also conducted by the existing distributed state estimator in [40-42] and the existing super-twisting algorithm in [43,44].The improvements and innovations of DFTE as well as the AESTW algorithm proposed in this paper will be demonstrated by the comparisons of simulation below.

Firstly, the position estimate errorepiand velocity estimate erroreqiof DFTE and distributed sliding-mode estimator in [40-42] are compared as are shown in Fig.13.

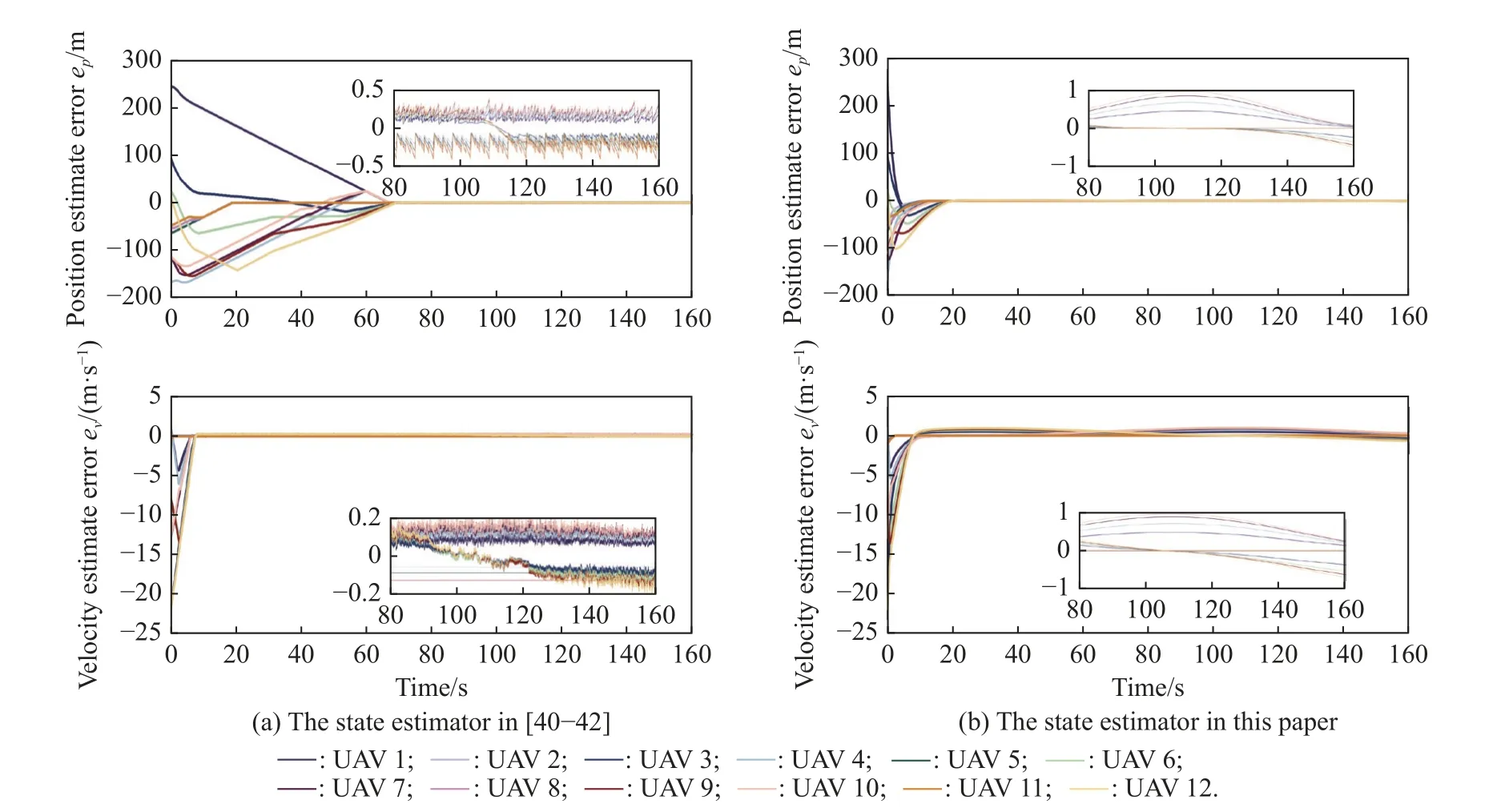
Fig.13 Position and velocity estimate errors of the DFTE in this paper and the estimator in [40-42]

It can be seen that the distributed sliding mode-state estimator proposed in [40-42] has significant chattering effects.By the contrast, when the same gains are chosen,the proposed DFTE has a clear advantage of faster convergence, less pronounced chattering effects, and much smoother transient process.

Remark 6 Regarding the estimate error, the theoretical analysis in Theorem 1 implies that the errors of the DFTEs will converge into a small enough constant neighborhood.By selecting the control parameters, the neighborhood can be adjusted to meet the precision requirement.In that way, the proposed DFTE can achieve a compromise between the precision and the chattering effects.

As a further step, the comparative simulations are carried out with the proposed algorithm, the conventional super-twisting algorithm in [43], and the fast super-twisting algorithm in [44] to verify the superiority of the proposed AESTW algorithm.The parameters of the conventionalsuper-twistingalgorithmarechosenasl1=10andl2=15, and theparametersofthe fastsuper-twisting algorithm are selected asl1=10,l2=15,l3=10,l4=15,while the parameters of AESTW follow the previous data.Taking thex-orientation control of the leader 1, the variations of the sliding mode variables are contrasted as shown in Fig.14.

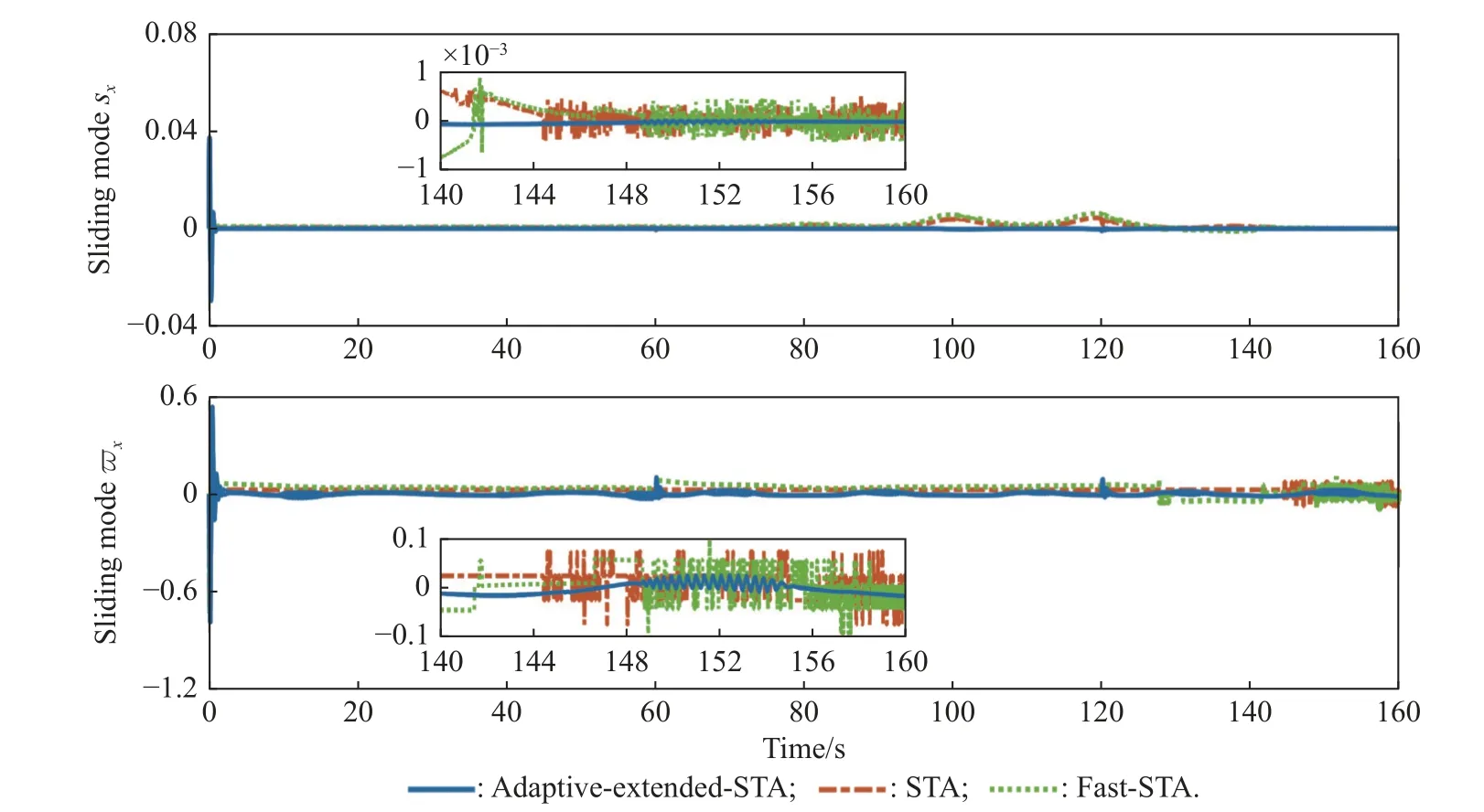
Fig.14 Variation comparison of x-orientation sliding mode variables of UAV 1

In comparison, it is clear that the AESTW algorithm in this paper has smoother sliding mode variations and significantly weaken the chattering effects compared with the conventional super-twisting algorithm in [43] and the fast super-twisting algorithm in [44].

4.4 Robustness verification

In order to verify the robustness of the proposed controller, a Monte Carlo simulation test is conducted.Aerodynamic parametersCD0,CL0,of each UAV are randomly uniformly perturbed within ±30% range.

Moreover, each UAV may encounter actuator faults and sensor faults at random instants.The efficiency losses of the thrust, angle of attack, and banking angle are randomly within 30% , 25% , and 25%.The bias of the thrust,angleofattack, andbanking angleare randomly within5N,2◦,and5◦.Atotalof 500 simulationsare conducted together.The results are shown in Fig.15, and it is obvious that the response has good consistency and the dynamic performance robustness can be realized.

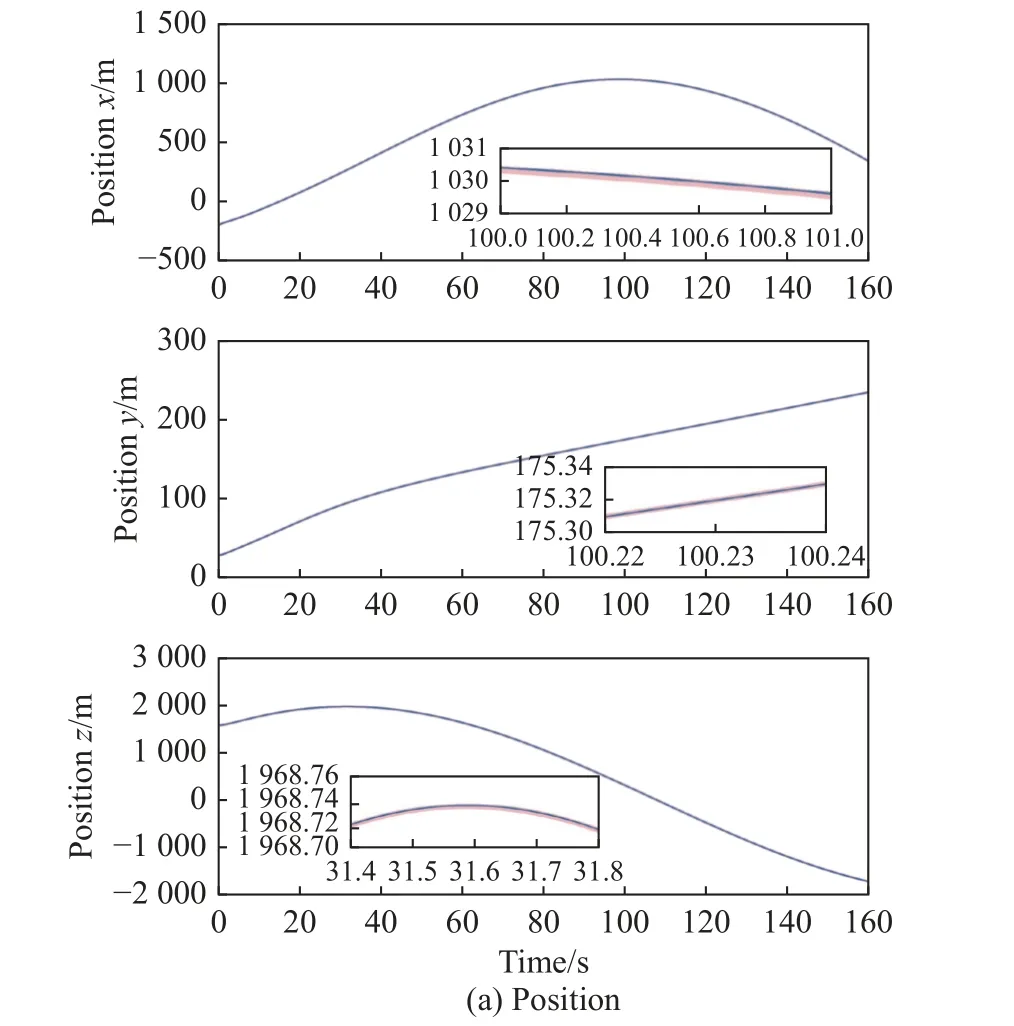
Fig.15 Results of UAV 1 in 500 Monte Carlo simulations

5.Conclusions

This paper aims to present a novel two-layer distributed fault-tolerant formation-containment control scheme for“multi-leader-multi-follower” fixed-wing UAV swarm realizing formation, dynamic target tracking in 3D space under model uncertainties and actuator and sensor faults.With only a part of leader UAVs acquiring the dynamic target’s states, the proposed DFTE can generate each UAV’s reference trajectory which meets the control objectives in a finite-time.Compared with the previous work, the trajectories generated by DFTE vary more smoothly with less chattering effects.Further, a distributed composite FTC framework is designed to rapidly and precisely track the generated reference trajectory.The composite FTC comprises the FTESO to compensate the integrated disturbance and a novel AESTW algorithm based on integral terminal sliding modes to enhance the system robustness with less chattering effect.Stability and finite-time characteristic of the closed-loop system are proved by Lyapunov theory.Comparison simulations verify the effectiveness and competitiveness of the proposed control framework in the formation-containment control of the fixed-wing UAV swarm for dynamic target tracking under the faults and time-varying disturbances.Overall, the proposed controller possesses advantages and improvements in fault tolerance, convergence time and less chattering effect.For the research of the next step, a control scheme under the circumstance of actuator saturation and multiple environmental obstacles could be considered to further improve the controller effectiveness and system safety in more general application scenarios.