A general evaluation system for optimal selection performance of radar clutter model

YANG Wei, ZHANG Liang, YANG Liru, ZHANG Wenpeng, and SHEN Qinmu

College of Electronic Science and Technology, National University of Defense Technology, Changsha 410073, China

Abstract: The optimal selection of radar clutter model is the premise of target detection, tracking, recognition, and cognitive waveform design in clutter background.Clutter characterization models are usually derived by mathematical simplification or empirical data fitting.However, the lack of standard model labels is a challenge in the optimal selection process.To solve this problem, a general three-level evaluation system for the model selection performance is proposed, including model selection accuracy index based on simulation data, fit goodness indexs based on the optimally selected model, and evaluation index based on the supporting performance to its third-party.The three-level evaluation system can more comprehensively and accurately describe the selection performance of the radar clutter model in different ways, and can be popularized and applied to the evaluation of other similar characterization model selection.

Keywords: radar clutter, clutter characterization model, model selection, performance evaluation.

1.Introduction

Clutter refers to the natural environment reflection echo other than the target echo received by the radar, mainly including meteorological, ground, and sea environment echo.It is an important factor in radar waveform design,target detection, tracking and recognition.There are many studies on environmental attribute classification by extracting some clutter features, such as the classification of weather or bird [1-3], land or sea [4,5], and the discrimination of ionospheric [6-8].The environmental ontology attribute has relatively clear label information,so it has relatively objective evaluation indicators such as classification accuracy.

In addition, scholars have carried out a variaty of analysis on various natural environment electromagnetic scattering coefficients, amplitude fluctuation statistical characteristics and spatio-temporal correlation characteristics of environmental echoes.Based on mathematical simplification derivation or empirical data fitting, the characterization models of radar clutter such as scattering coefficient[9-12], amplitude fluctuation statistics [12-15], power spectrum [12,16] and Doppler spectrum [17,18] are studied in detail.Since most scattering coefficient models only have good fitting effect on clutter scattering data in a specific environment and are not suitable for all radar application scenarios [13], their applications are limited.However, the amplitude fluctuation statistics, power, and Doppler spectrum models are widely used.

At present, more than 50 kinds of empirical or theoretical characterization models such as amplitude fluctuation statistics, power, and Doppler spectrum have been proposed.How to select the characterization model optimally in practical application has attracted great attention of scholars.Especially, since cognitive radar technology gradually became a research hotspot in the field, the demand for real-time perception and fine characterization of radar clutter environment has become more and more urgent.The refined characterization of radar clutter is represented by its corresponding optimal selection of radar clutter model, which has a profound impact on cognitive waveform design [19], constant false alarm rate(CFAR) detection [20], multi-target tracking [21], and target recognition under clutter background [22].Different from the previous environmental attribute classification based on clutter features, clutter model for real radar data does not have an objective label in hand.How to describe the quality quantitatively for optimal selection of radar clutter model has become an urgent theoretical and technical problem.

In the existing research, two ways are mainly used to evaluate the optimal selection performance of clutter model.One is to transform the model selection problem to a classification problem, classify its characterization model based on the simulation clutter data with clear model label [23-26], and then evaluate it by using the classification accuracy.For measured clutter data without real model label, the goodness of fit index is used to optimal selection and evaluate its performance [27-30].Zhan et al.[26] proposed to comprehensively use the above two methods for evaluation.These two evaluation methods are to evaluate the accuracy of clutter model optimization.In fact, the optimal selection purpose of clutter model is to provide a priori information support for radar waveform design, target detection, tracking and recognition.It is more persuasive to introduce the thirdparty task performance as the effectiveness evaluation index of optimal model selection.In order to describe the selection performance of clutter model more comprehensively and accurately, this paper constructs a three-level evaluation system (TEST), which can be used as a comprehensive toolkit for the evaluation, improvement, and optimization of clutter characterization models.

The subsequent structure arrangement of this paper is as follows.Section 2 focuses on establishing the threelevel evaluation framework for the optimal selection performance of radar clutter model.Section 3 presents the calculation basis and method of the three-level evaluation index in detail.And Section 4 summarizes the paper.

2.Three-level evaluation framework for optimal selection performance of clutter model

Since the purpose of optimal clutter model selection is to provide clutter priori information for third-party tasks such as radar waveform design and target detection, it is necessary to ensure the accuracy and effectiveness of model information at the same time.

The accuracy of clutter model selection can be evaluated from two aspects.First, for the clutter data with clear model label, the characterization model is classified, and the classification accuracy is evaluated as usual.That is the ratio of the number of samples consistent with the real label of the characterization model to the total number of samples.It is the most intuitive and commonly used index to judge the performance of classification methods in classification problems.The key to obtain the classification accuracy is to have a batch of samples with clear category labels.Since the radar clutter data itself does not have the label of the characterization model, such samples can be constructed by simulation only.

Second, characterization models such as amplitude fluctuation statistics, power, and Doppler spectrum of radar clutter can be determined by the coincidence of theoretical characterization models, which can also be used to judge the accuracy of clutter model selection.Based on this idea, the fitting accuracy between the selected model and the measured clutter data can be computed for multiple clutter data samples without model label, and its statistical results is just the accuracy of the model selection.For example, to evaluate the optimal selection performance of an amplitude fluctuation model of measured clutter data, the finally selected model is used to complete the relevant parameter estimation based on the measured clutter data.Then, the goodness of fit between the selected theoretical characterization model and the measured clutter data can be statistically scored by using Akaike information criterion (AIC) [27], Kolmogorov-Smirnov (K-S) measure [28], Kullback-Leibler(KL) divergence [29], and mean squence error (MSE)measure [30].

In addition, the effectiveness of clutter model selection is judged according to its effect in subsequent applications.Therefore, it needs to be implemented in combination with tasks such as radar waveform design, target detection, tracking, and recognition.For example, the CFAR detection of radar target under clutter background needs to first select the clutter amplitude fluctuation statistical model and use the reference unit to complete the relevant parameter estimation.If the selected clutter amplitude fluctuation statistical model is not well, the target detection result will be unsatisfactory.Therefore, the selection effectiveness of clutter amplitude fluctuation statistical model can be evaluated according to the target detection effect.

Based on the above analysis, a TEST is constructed.The first level is based on the model optimization accuracy index via the simulation data.The goodness of fit index based on the selected model is adopted.The evaluation index supporting the third-party performance, which can be used to evaluate the performance of the clutter model selection algorithm is constructed by the third level.The structural diagram of TEST is shown in Fig.1.

Fig.1 TEST for clutter model optimization

3.Calculation basis and methods of TEST indexs

The TEST of clutter model selection performance is completed by the statistical measurement of three types of indicators.The calculation basis and methods are explained below.

3.1 The first level evaluation: model selection accuracy index based on simulation data

For clutter simulation data with real labels, the optimization of its characterization model is the classification problem.Accuracy is the percentage of the correct number of samples classified by the classification algorithm to the total number of samples.It is also an important index to evaluate the accuracy of the classification algorithm.It can be calculated according to

where,pis the classification accuracy,nis the number of correctly classified samples, andNis the total number of samples.According to above analysis, the closer the value ofpis to 1, the classification algorithm is the better.

The premise to calculate above accuracy is that the sample has a category label that can test whether the classification is accurate.Because the measured clutter data itself has no clear model label, the clutter data samples with clear model label can only be obtained through simulation.In addition, the performance of any model selection algorithm needs to be compared with others, and the comparison results can provide a basis for subsequent algorithm application.

To sum up, the first level evaluation of TEST includes three steps.Firstly, the clutter models of tagged clutter simulation data are optimally selected by using the algorithm to be evaluated and the comparison algorithms;Secondly, the selection accuracy is calculated according to the results of each algorithm; Finally, the performance of the model selection can be scored according to the accuracy evaluation.Fig.2 indicates the first level evaluation process.

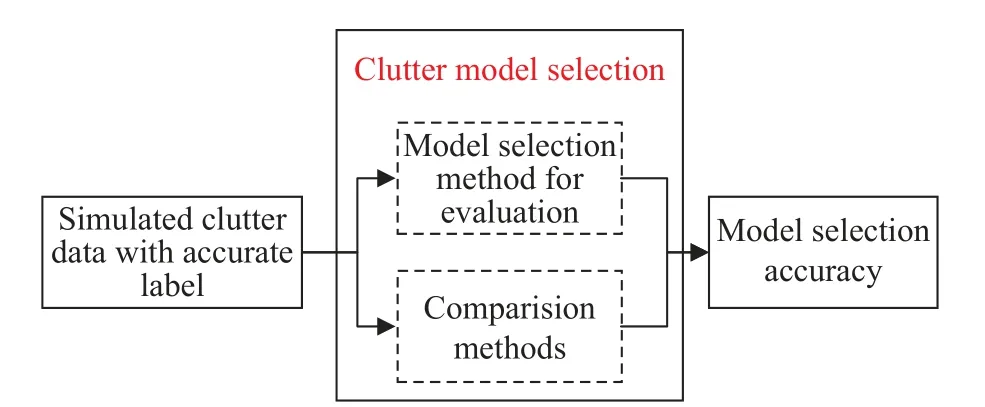
Fig.2 The first level assessment

3.2 The second level evaluation: goodness of fit index based on the selection model

For the unlabeled measured clutter data, the fitting matching method can be used for model selection.Fig.3(a) is a comparison between the nonparametric clutter amplitude probability density curve obtained by histogram statistics and the fitting Rayleigh distribution probability density curve.Fig.3(b) is a comparison between the nonparametric clutter power spectrum curve obtained from the periodic diagram and the fitting exponential power spectrum curve.Fig.3 shows that the nonparametric amplitude probability density curve and power spectrum curve of clutter are different from their corresponding theoretical curves.This difference can be quantified by KL divergence, MSE measurement, AIC, and K-S distance.These indicators are called clutter goodness of fit indicators.

Fig.3 Clutter model curve

(i) KL divergence:

wheref(·) is the nonparametric probability statistical distribution of clutter data amplitude, andq(·) is the theoretical characterization model used to fit clutter data.

(ii) MSE metrics:

whereNis the sample length.

(iii) AIC:

where lnL(θ) is the maximum likelihood function of the theoretical characterization modelq(x) used to fit clutter data, θ is the parameter vector, andKis the number of parameters.

(iv) K-S distance:

whereF(x) is the nonparametric probability cumulative distribution of clutter data amplitude, andQ(x) is the theoretical characterization model used to fit clutter data.

The clutter goodness of fit index can directly reflect the gap between the optimal theoretical characterization model curve and the nonparametric clutter curve.The smaller the gap is, the better the theoretical model fitting clutter data.By comparing the differences between various parametric model and nonparametric clutter curves,the model with the best clutter fitting effect can be selected.In view of this, the second level evaluation of TEST uses statistics (such as mean and variance) of goodness of fit index of multiple clutter samples to evaluate the accuracy of model selection algorithms.

To sum up, the second level evaluation of TEST also includes three steps: Firstly, the clutter models of unlabeled clutter data are optimally selected by using the algorithm to be evaluated and the comparison algorithms,and a set of unified model parameter estimation methods is adopted for different selection models; Secondly, one or more clutter fitting accuracy indexes are selected, and the corresponding fitting accuracy index can be calculated for the selection results of each algorithm and clutter data; Finally, the mean and variance of these index values can be calculated, and the accuracy of clutter model selection is scored according to these values.Fig.4 indicates the second level evaluation process.

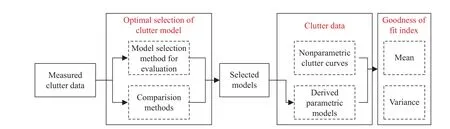
Fig.4 The second level assessment

It is worth noting that the specific calculation results of goodness of fit index are affected by the parameter estimation methods.While based on large test samples, a set of unified model parameter estimation methods is adopted for the same selection model, which will effectively smooth and suppress the impact of parameter estimation methods on the evaluation of selection algorithm.Therefore, the final ranking result of goodness of fit index is relatively objective.

3.3 The third level evaluation: model selection effectiveness based on supporting the performance of the third party

Radar target detection and recognition can be interfered by clutter, so it is necessary to take targeted clutter suppression measures according to clutter model.Whether the results of clutter model selection are effective for radar waveform design, target detection, tracking, and recognition needs to be verified by third-party tasks.Therefore, the third level evaluation of model selection performance is to quantify the support effect of thirdparty tasks.

To sum up, the third level evaluation of TEST includes three steps: Firstly, the clutter models of unlabeled clutter data are optimally selected by using the algorithm to be evaluated and the comparison algorithms respectively; Secondly, the adopted third-party task is implemented based on the selection model, and the performance index of this third-party task is obtained;Finally, the effectiveness of the clutter model selection is scored according to the performance index of this third-party task.Table 1 shows some third-party tasks applicable to the implementation of the third level evaluation and their corresponding typical performance indicators.Fig.5 indicates the third level evaluation process.

Table 1 The third-party tasks used in the three-level evaluation and its corresponding typical performance index

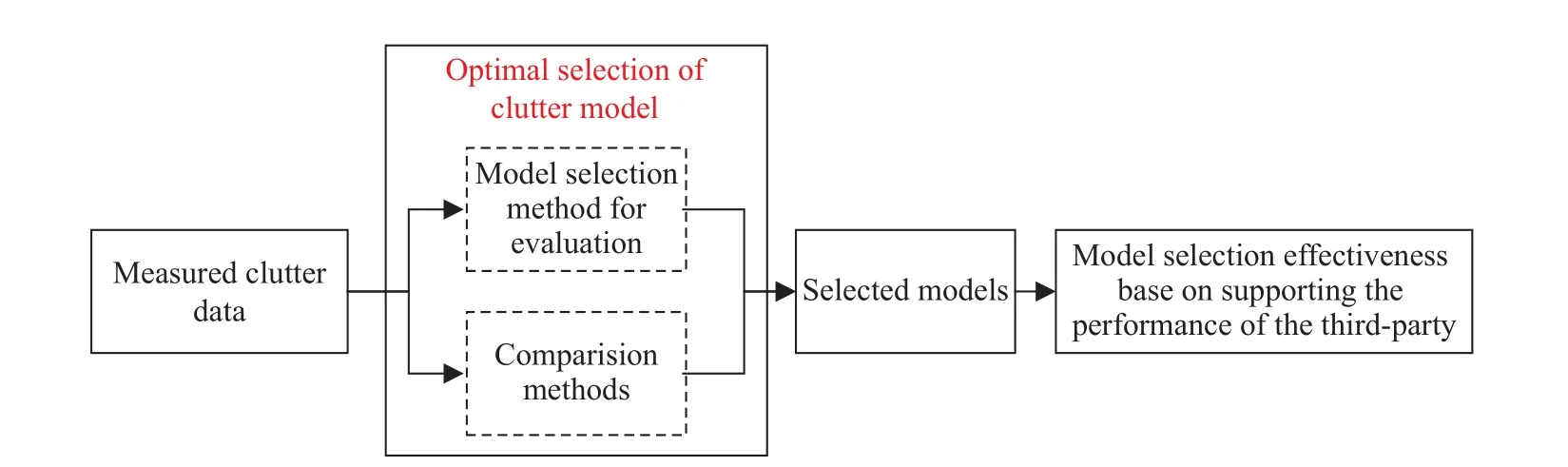
Fig.5 The third level assessment

Note that the three-level evaluation in TEST uses statistics as the performance indexs, which can reduce the random error and ensure the reliability of the evaluation index.

4.Conclusions

Clutter model selection is an important step of target detection, tracking, and recognition and radar waveform design in clutter background.Its accuracy and effectiveness are directly related to the performance of these tasks.In this paper, a general three-level evaluation system for model selection is proposed and constructed for the first time, which can comprehensively and accurately quantify the accuracy and effectiveness of optimal selection in different ways.It has important theoretical and application value for the evaluation, improvement, and optimization of clutter characterization model.In the future, based on this work, the constant false alarm detection and waveform optimization technology of radar target based on clutter model selection will be studied.