K-DSA for the multiple traveling salesman problem
2024-01-17TONGShengQUHongandXUEJunjie
TONG Sheng, QU Hong, and XUE Junjie
Air Traffic Control and Navigation College, Air Force Engineering University, Xi’an 710051, China
Abstract: Aimed at a multiple traveling salesman problem(MTSP) with multiple depots and closed paths, this paper proposes a k-means clustering donkey and a smuggler algorithm (KDSA).The algorithm first uses the k-means clustering method to divide all cities into several categories based on the center of various samples; the large-scale MTSP is divided into multiple separate traveling salesman problems (TSPs), and the TSP is solved through the DSA.The proposed algorithm adopts a solution strategy of clustering first and then carrying out, which can not only greatly reduce the search space of the algorithm but also make the search space more fully explored so that the optimal solution of the problem can be more quickly obtained.The experimental results from solving several test cases in the TSPLIB database show that compared with other related intelligent algorithms, the K-DSA has good solving performance and computational efficiency in MTSPs of different scales, especially with large-scale MTSP and when the convergence speed is faster; thus, the advantages of this algorithm are more obvious compared to other algorithms.
Keywords: k-means clustering, donkey and smuggler algorithm(DSA), multiple traveling salesman problem (MTSP), multiple depots and closed paths.
1.Introduction
The traveling salesman problem (TSP) is one of the classic non-deterministic polynomial (NP)-hard problems in the field of combinatorial optimization.It has a simple description but is difficult to solve, thus the problem has been widely studied by numerous scholars.After decades of development, the TSP has made considerable progress.Some efficient algorithms, including branch and bound algorithms, local search algorithms, simulated annealing,Tabu search, and evolutionary calculations, have been introduced to solve TSP [1].The TSP can usually be divided into a symmetric model (symmetric-multiple TSP(MTSP)) [2] and an asymmetric model (asymmetric-MTSP) [3].
According to the methods differences of path generation, the intelligent optimization algorithm for the TSP can be divided into two categories.The first category is the path-building algorithm, which starts with a city to search for a feasible path based on some degree of greedy strategy, such as the Tabu search algorithm [4] and the ant colony algorithm [5].The second category is the whole exploration algorithm, for instance the genetic algorithm [6], particle swarm optimization (PSO) [7], and the differential evolution algorithm [8].They generate new solutions through some kind of holistic search strategy and have better global exploration capability, but these algorithms often need to fix new illegal solutions.However, the restoration of a new solution destroys the process of population evolution, therefore, local search strategies need to be adopted to improve the algorithm’s local development capability.Over the years, to better understand the balance between global search and local development in the population evolution process, some emerging intelligent optimization algorithms have been used to solve the TSP [8-11].
The MTSP has a substantial practical application background.Since the TSP has been proven to be an NP-hard problem [12] and the MTSP requires both group optimization and traversal order within the group, the MTSP is also an NP-hard problem [13].With the continuous accumulation of TSP research results and the need for a change in social development, the MTSP has received increasing attention.Many practical problems can be described by the MTSP, for example, scheduling problems in the printing process [14], personnel scheduling problems [15], school bus driving path problems [16], interview scheduling problems [17], route planning [18,19], and slab rolling plans for steel companies [20].
Since the MTSP has received extensive attention in recent years, its solving speed and efficiency has made important theoretical significance and practical application value.Carter et al.[21] proposed a two-segment chromosome encoding method based on the genetic algorithm and designed a corresponding genetic operator to solve the MTSP with the shortest total distance, which greatly reduced the understanding of this space and eliminated a redundant solution.Zhou et al.[22] proposed three algorithms for a multi-depot closed-loop MTSP and proved the superiority of the improved partheno genetic algorithm in solving this problem.Singh et al.[23] drew on the idea of biological intelligence and used the artificial bee colony algorithm and invasive weed optimization algorithm to solve the MTSP, which improved the accuracy of the solution.Ren et al.[24] introduced a general genetic algorithm based on the polar coordinate system to solve the MTSP.Bektas [25] gave a detailed overview of the formulation and solution of the MTSP.
Fang et al.[26] modelled the multiple unmanned aerial vehicles (UAVs) cooperative reconnaissance problem as multi-depot MTSP (MMTSP) and solved it using genetic algorithm.Hou et al.[27] simplified complex MMTSP directed graphs, proposed effective algorithms based on the simplified results, and optimized the general results using 2-opt.Ramadhani et al.[28] used ant colony algorithm to solve the MMTSP with a fixed starting point and confirmed that choosing a different city as the starting point will have a certain impact on the solution.Koubaa et al.[29] proposed a distributed algorithm to solve the MMTSP and confirmed that the algorithm is superior to the centralized genetic algorithm in solving this problem.Zhou et al.[30] proposed two single-parent genetic algorithms and particle swarm optimization for solving the MMTSP.
This paper studies the MTSP with multiple depots and closed paths.Compared to the model with the MTSP with a single depot, this model has been analyzed by relatively few studies.
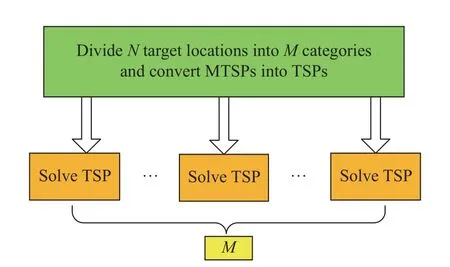
Facing the large scale MTSP with hundreds of target points, the conventional grouping genetic algorithm is not ideal.For finding paths in a huge search space, genetic algorithms can never guarantee the optimal solution.To improve the calculation efficiency and planning results,this paper proposes a stepwise combination optimization algorithm based on thek-means clustering algorithm and the donkey and smuggler algorithm (DSA) to solve the MTSP.The proposed algorithm divides a big problem into several sub problems.This paper cleverly uses the DSA andk-means clustering to solve the MTSP flexibly.This algorithm improves the global search ability of the algorithm and shortens the execution time of solving the best path.It provides a novel idea for solving the MTSP,which is worthy of further study.
2.Preliminaries
2.1 Description of the MTSP with multiple depots and closed paths
This paper studies the MTSP with multiple closed paths,which can be briefly described as follows: there is a set of cities from 1 ton,v1,v2,···,vn, traversed bymtraveling salesmen (for cityvi, the coordinate is (xi,yi)).Then they are distributed into different cities (excluding the starting city).Now, letmtraveling salesmen traverse some cities separately, and finally, make the sum of the city paths traversed by each traveling salesmen the shortest.That is, to divideV={v1,v2,···,vn} intomnonempty subsetsthe path with smallest cost that passes through each subset needs to be found.Then,mtraveling salesmen have to traverse the remainingn-mcities completely.Finally,they should all return to the departure cities.Except for the cities wheremtraveling salesmen are located, the rest of the cities are visited by a traveling salesman once; the distance between the two cities is indicated byci j(i,j∈{v1,v2,···,vn}) , andcij=cji(cij+cjk>cik).
2.2 k-means clustering
Clustering is the process of assigning samples to different classes [31].In general, in the clustering results,samples within same category show greater similarity,while different types of samples show greater dissimilarity.The goal of clustering is to divide the data based on a specific similarity measure.The concept of clustering originate in many subject areas, including mathematics,computer science, statistics, biology, and economics.There are clustering techniques suitable for different fields, and they are used to measure the similarity between data points, so as to effectively divide the samples in this field.
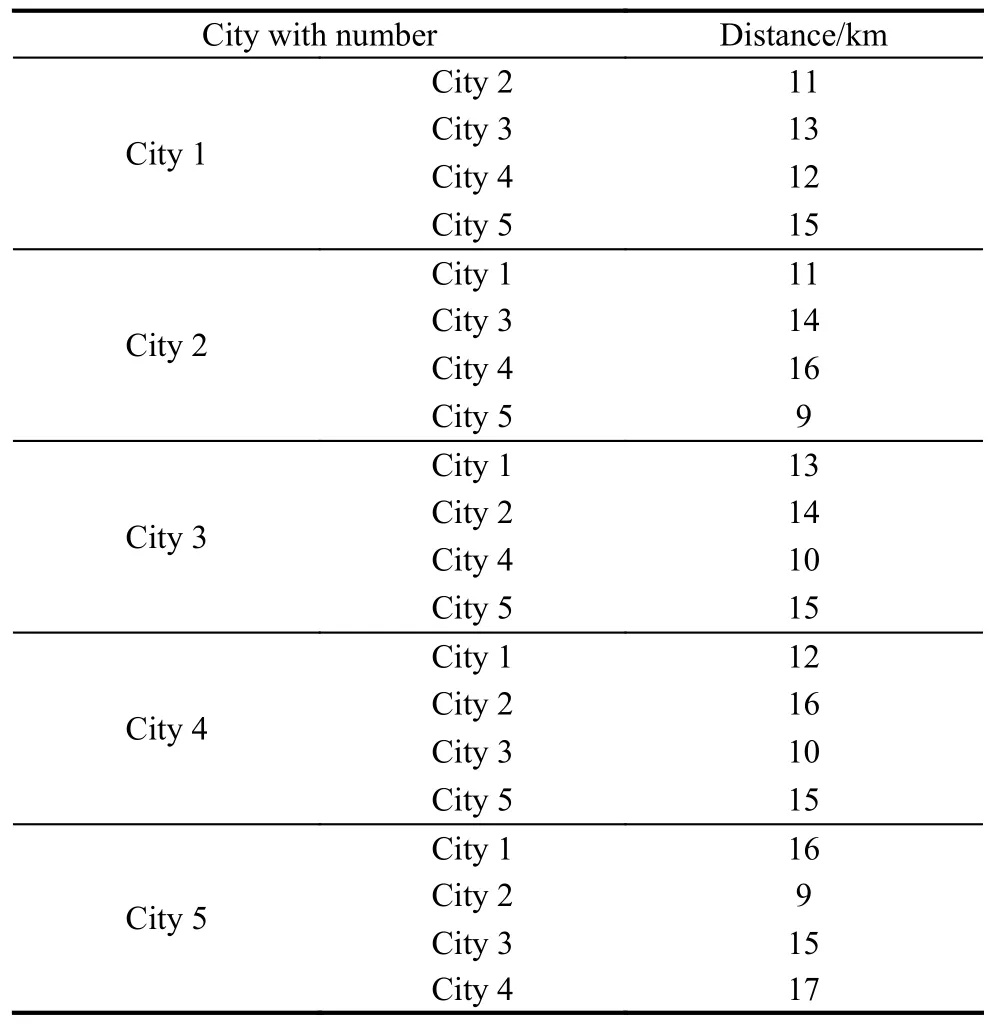
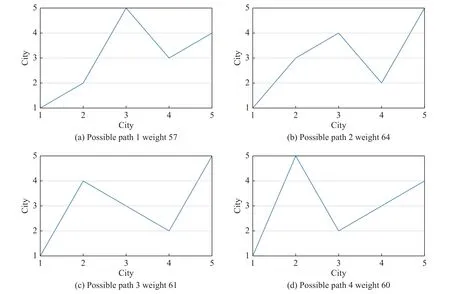
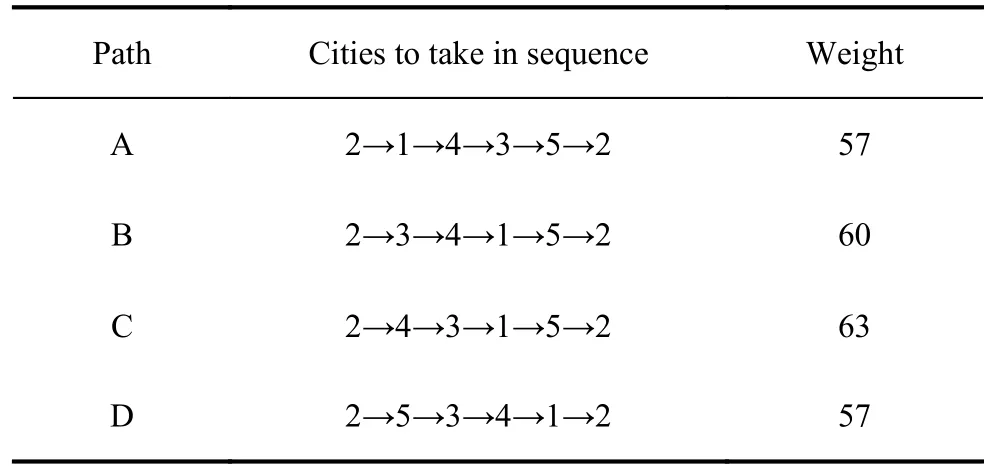
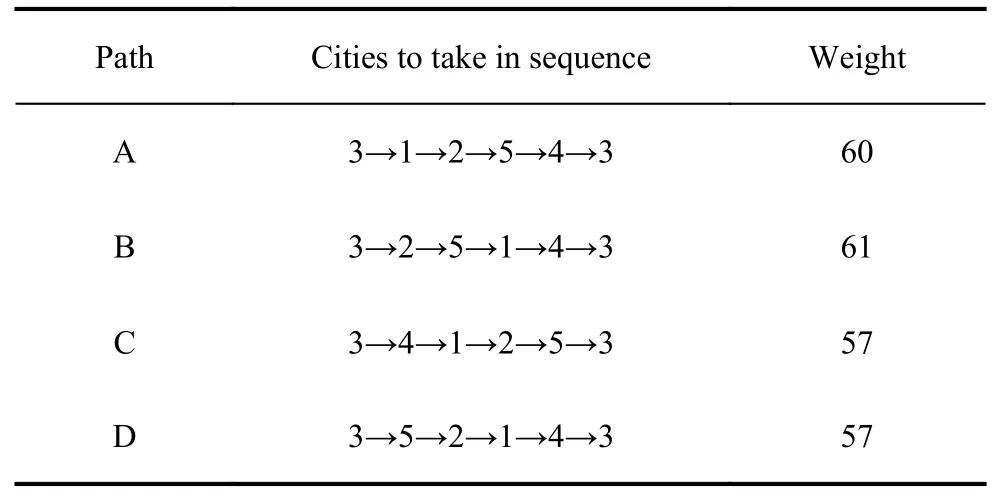
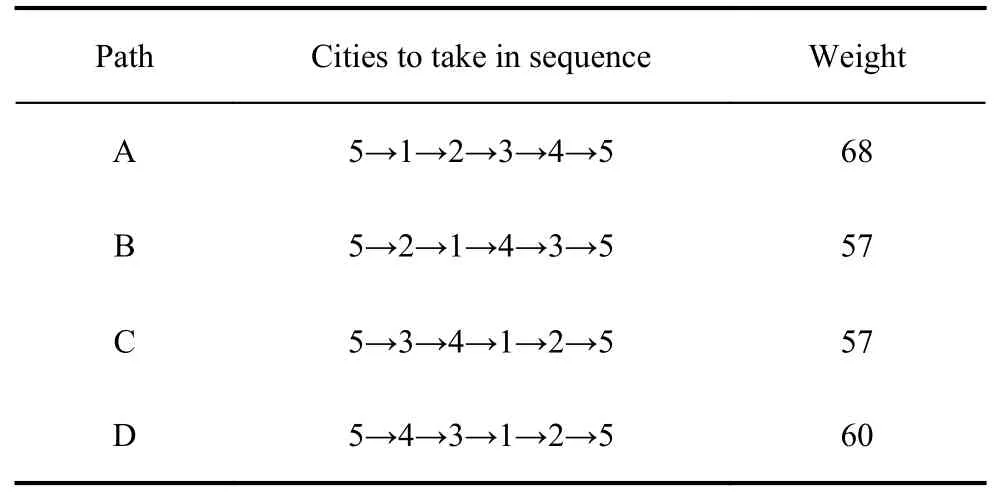
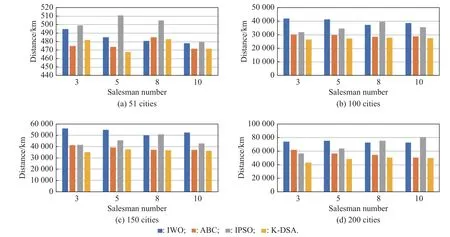
Partitioning clustering means that for a given data set,a split method will be used to constructKgroups, with each group representing a cluster,K Among the many clustering methods, thek-means clustering method is the most classic and the most widely used clustering method [37,38].This method, continuously iterates with the center of various samples as the representative and is only applicable to numerical attribute data.The type of clustering has a good clustering effect on super-spherical and convex data. LetX={x1,x2,···,xi,···,xn} be the data innRdspaces.Before clustering begins,kis specified as the initial number of clusters.For choosingk, it can be either randomly or chosen according to the number of samples.The basic working process of thek-means algorithm is as follows: first, selectkobjects fromndata objects as the initial clustering center.The formula for calculating the similarity is as follows.Assuming thatCjis the center of thejth class, the distance and similarity betweenxiandCjare as follows: Then repeat this process. Generally, mean square error is used as the standard clustering measure function, and its form is The inside of the cluster is as compact as possible, and different classes are separated as much as possible. Donkeys have good memory and quick and easy learning ability, which can distinguish themselves from other animals to a certain extent.According to the relevant research, the learning ability of donkeys can be as strong as that of dogs.The intelligence quotient (IQ) of an adult donkey can be equivalent to that of a seven-year-old human child and can be slowly improved through acquired training.These characteristics have made the donkey the largest smuggling animal in domestic and international smuggling activities for years. It is pointed out that smugglers often use donkeys for smuggling business.On familiar roads, donkeys can carry out smuggling activities on their own without the guidance of smugglers.According to a UK press release“Daily Mail”, that donkeys are used to smuggle stolen cars from Zimbabwe to the border of South Africa by smugglers, as shown in Fig.1. Fig.1 Smuggling crime assisted by donkey Donkeys are trained by domesticators.Smugglers wear police uniforms at the border and begin to attack the donkeys with stones, so that the donkeys can recognize these uniforms and avoid them.That is, donkeys will change direction or escape once they recognize these uniforms. Donkeys also have high regional characteristics, and they usually live alone or in groups of two [39].When donkeys feel danger, escaping may lead to lethality.Their fighting and defensive behavior will trigger them to protect themselves.Another behavior of a donkey is suicide.It is written in “Visual World” that a donkey will choose to commit suicide when it is cruelly abused by its owner,see Fig.2. Fig.2 Suicide behavior chosen by donkey In addition, donkeys also show mutual supportive behavior.ABC News show (see Fig.3) that a donkey failed to escape from the fence.Then it soon receives assistance from its companion by taking off the wooden stick to help them out. Fig.3 Assistance between donkeys The donkeys’ behavior can be summarized as follows:escape, face and support, or face and suicide. (i) They escape from people or experiences that have caused them pain in the past. (ii) Their combat or defense mechanism will be triggered when they sense danger. (iii) They support each other when encountering difficulties or needing help. (iv) When conditions reach an unbearable level, the donkey will commit suicide. The behavior of one donkey can be summarized as follows: escape, confront and support, or confront and suicide.The DSA simulates the behavior of the donkey and the smuggler.A two-part algorithm is then established which is able to achieve the optimal solution and to respond to changes while maintaining the optimal solution.The “smuggler” part is the nonadaptive part of the DSA, which means that this part does not adapt to any changes.So, smugglers will review all possible paths,then determine the best route to take based on certain metrics (such as timing and survivability). Firstly, determine the parameters of each solution.Then, use the following formula to calculate the applicability of each possible solution, grouping all possible solutions according to the fitness value of each possible solution: wherexijis the possible solution;imeans the number of possible solutions;jis proportional to the number of parameters of each possible solution;zis inversely proportional to the number of parameters for each possible solution.The numerator contains parameters that are proportional to the ratio.Finally, pick the best solution(which has the smallest fitness), and send it to the donkey according to the solution. In the adaptive (donkey) part, the decision is based on the current task state.First, apply the optimal solution identified in the smugglers section.Second, evaluate the current solution based on adaptability (in the case of adaptability changes, the adaptability function will continue to be used to find a better solution).Then determine whether the current solution is congested.If so, the following steps should be taken. (i) Escape: re-assess and update the best solution.This behavior is to change the current path to another best path(best solution), and when the best solution determined in the non-adaptive part of the algorithm is no longer the best solution, it will be discarded, and new best solutions based on new changes will be set. (ii) Confront and suicide: repair the best path currently in use (optimize the best path).At the same time, delete the current path and use another best solution to repair the blocked possible solution, without recalculating the overall applicability of the possible solution.If the best solution set in the first part of the algorithm is no longer the optimal solution due to any changes that affect the adaptability of the algorithm, then we will keep the solution first.Then, put the solution back to its original state until the second-best solution in the solution set can be utilized. The fitness value of the best solution is the smallest.Through (6), we can use the second-best solution among other solutions as the best solution.There is no need to reassess the overall suitability of other possible solutions. (iii) Confront and support: when overload starts to appear, assign the sub-optimal solutions avoiding discarding this solution until the signs of overload disappear.Two channels can be used to reduce overload.When the best route overloaded, use the second-best for substitution.It is unnecessary to re-assess the overall applicability of possible solutions. Equation (7) represents the second-best solution determination.Then, the best solution and suboptimal solution are combined by (8). Below is a detailed explanation of the DSA using a specific TSP.Consider TSP with five cities, with the distance between the five cities being given by matrixd, as shown in Table 1. Table 1 Matrix d of the distance between five cities For the first iteration of the DSA, the smuggler checks all the distances between the two cities in the first part of the algorithm, and based on his or her experience,determines the shortest path from each city.The step will loop to achieve the shortest path from a different city to all other cities.The algorithm examines each city point as starting point to achieve all possible routes with distances as well as the shortest path to follow.Fig.4 shows the best road map of the first part of the DSA (the smuggler).Among them, the execution time of the first part took around 0.028 5 s, and the shortest route and its shortest distance from each starting point are listed in Table 2. Fig.4 Shortest paths to be taken to finish the salesman tour Table 2 The first part of the algorithm provided all the possible paths and their weights The second part of the algorithm maintains routes to all city points when the shortest path selected in the first part is no longer available.In this part, after determining the starting city and shortest path, the algorithm will scan the entire data set and calculate all other possible paths and distances from this city point to all city points in the set.The first part of the DSA solves the best path from each city point.The distance of the best path from city points 1, 2, 3, and 5 is the same, which is 57.Therefore, we can use the second part of the algorithm.Select points 1, 2, 3,and 5 as the starting point.The possible route starting point from the city point “1” and the distance it passes are shown in Fig.5. Fig.5 The shortest path and the other possible paths that can be taken from the city one to visit all the other cities The execution time of the second part is 0.012 6 s, and the possible route from city point “1” and the distance it passes are listed in Table 3. Table 3 Possible paths from City 1 with different weights If the possible route is from city point “2”, the other possible paths will be shown in Table 4.If the possible route is from city point “3”, then the other possible paths will be shown in Table 5. Table 4 Possible paths from City 2 with different weights Table 5 Possible paths from City 3 with different weights If the possible route is from city point “5”, then the other possible paths will be shown in Table 6. Table 6 Possible paths from City 5 with different weights To analyze the performance of the algorithm, this paper uses the ant colony optimization (ACO) to independently run the solution with 16 executions and 100 iterations for each execution.The results are shown in Table 7. Table 7 Results of ACO running 16 executions The best solution for this distance matrix is [1, 2, 5, 3,4, 1] with a weight of 57, and from the execution results above, we can see that this solution appeared three times out of 16 executions and it is not stable; thus, it may or may not appear from in the first execution. The execution time of each ACO operation is between 0.11 s and 0.15 s.At the same time, after the DSA found the optimal route starting from each city point, the adaptive part of the algorithm provided other alternative suboptimal route solutions starting from the city point.The ACO can only obtain the optimal route starting from a possible city point.If other changes occur in the optimal route to be solved, then it is not able to provide alternative solutions to the suboptimal route.From the above analysis, it can be concluded that, compared with the ACO, the DSA can provide more and stable route options in a shorter time. To solve the multistart closed-loop MTSP problem, especially for the situation where the number of target locations increases to hundreds, a stepwise combination optimization algorithm is designed.The algorithm structure is shown in Fig.6.The first step is to use thek-means clustering algorithm to decompose the MTSP intomindependent TSPs; the second step is to use the DSA to solve themTSPs separately and find the minimum path solution for each TSP. Fig.6 Combination of the clustering algorithm with the DSA Thek-means algorithm is one of the most commonly used algorithms for cluster analysis.The algorithm is simple and fast and can effectively handle large datasets.Thekmeans clustering algorithm first randomly selectmobjects fromndata objects as the initial clustering center.For the rest of the objects, according to their similarity(distance) with these cluster centers, they are assigned to the most similar clusters.Then, the mean of all objects in the cluster is calculated as the new cluster center; this process is repeated continuously until the standard criterion function starts to converge. Thek-means clustering algorithm is used to decompose the MTSP problem intomindependent TSP problems.The specific steps are as follows: (i) Randomly selectmtarget points as the initial center point, such asC1=T1,C2=T2,···,Cm=Tm. (ii) Calculate the distance between each target point andmcenter points in turn, and divide each target point into the cluster where the nearest center point is located according to the principle of minimum distance; that is, His smile deepened, but he made no attempt to answer. A Mexican woman and two men were standing nearby. The woman stepped forward and eyed me inquiringly,. Carlos, he no speak English, she volunteered. You want I should tell him something? (iii) Update the position of the center point of each cluster, that is, calculate the average of all objects in the cluster. (iv) Repeat (ii) and (iii), until the position ofmcluster center points no longer changes. The steps to solve the DSA are as follows: Step 1 Nonadaptive (smugglers)(i) Determine the parameters of each solution. (ii) Use (7) to calculate the fitness value of each possible solution. (iii) Pick out the optimal solution then transmit it to the donkey. Step 2 Adaptive (donkey) (ii) Use (7) to evaluate the fitness value of the current solution.If its fitness value changes, then continue to use the fitness function to find the optimal solution. (iii) Determine whether the current optimal solution is congested.If so, then perform one of the following steps: i) Escape: use (5) to re-evaluate the fitness value of the possible solutions, then pick out the one with the lowest fitness value as the optimal result. ii) Confront and suicide: by using (5), the second best solution can be selected as the optimal one. iii) Confront and support: when achieved the overloaded optimal solution, use (5) to select the second-best possible solution to support the best.Then use (6) to combine the optimal and the suboptimal solution to creat the optimal support solution. The execution flow is shown in Fig.7. Fig.7 Execution flow of the DSA For the purpose of reflecting the performance of the K-DSA in this paper and solving the combinatorial optimization problem respectively, certain cases in the TSPLIB database are selected.Matlab 2018b is used for programming; the operating system is Windows 10, the CPU is I5-9300H, and the RAM is 16 G to test and experiment. In this subsection, we test the IPSO, IWO, ABC, and K-DSA against a MTSP in 100 cities with five salesmen.The results are shown in Fig.8. Fig.8 Solutions of the PSO, IPGA, ABC, and K-DSA In terms of the route result optimization graph, the K-DSA apparently shows better result than others.K-DSA has more advantages in the fluency and time-efficiency of path planning. In this subsection, we compare K-DSA with other intelligent algorithms.We study the relationship between the city numbers and the solution, then compare the results separately tested by four algorithms. This subsection compares IWO, ABC, and IPGA with K-DSA, with the number of cities being 51, 100, 150, and 200, and the number of traveling salesmen being 3, 5, 8,and 10, respectively for simulation.The results obtained are plotted into Table 8.To show the superiority of the KDSA more intuitively, three histograms are drawn based on the number of cities: 51, 100, 150, and 200, respectively, as illustrated in Fig.9. Fig.9 Solutions of different intelligent algorithms when n=51, 100, 150, or 200 From the results obtained, a conclusion can be drawn that K-DSA has certain advantages in solving the MTSP.As the number of cities increases, the gap between IWO, ABC, IPGA, and K-DSA gradually widens; that is,the superiority of the K-DSA’s solution becomes more obvious with the increase in city size.In the problem of each city scale, the optimal solution obtained by the K-DSA is relatively ideal, which shows that it can fully explore the search space of each group after solving each class as the TSP, thereby satisfying the optimal function solution. As can be seen from the data in the Table 9, the running time of the algorithm is less affected by the parameters and the optimal solution is less affected by the parameters, which indicates that its performance is steady and can adapt to various situations. Table 9 Effect of parameters on the results of K-DSA From the chart above, the K-DSA has the best performance in solving optimal solutions.We can also see that the K-DSA’s solution performance gradually improves as the number of cities increases. This paper proposes a novel hybrid metaheuristics algorithm for multiple travelling salesman problems with multiple depots and closed paths.This paper compared the K-DSA with other intelligent algorithms through dozens of MTSP standard test functions.Then through the parameter changes for the example, the performance of the algorithm for solving the optimal solution is tested.Experiments show that the K-DSA has better performance than that of other algorithms, especially under more complex environments.Meanwhile, the proposed algorithm is suitable for both the MTSP with multi-start and closed paths and single point as well.Accordingly,just modifying the fitness function method and associated coding is sufficient. The combinatorial optimization algorithm in this paper only provides a way to solve the MTSP from another angle, but does not solve the problem fundamentally.Except the methods used in the paper, some of the most representative computational intelligence algorithms can be used to solve the problems, like monarch butterfly optimization, earthworm optimization algorithm, elephant herding optimization, moth search algorithm, slime mould algorithm, and Harris hawks optimization.Our next focus is to solve the MTSP faster on the basis of more cities and more travelling salesmen and apply the algorithm to actual scenarios to solve related path-planning problems.
2.3 DSA



3.Applying DSA to the TSP





4.Applying the K-DSA to the MTSP
4.1 k-means clustering algorithm modelling
4.2 DSA modeling

5.Simulation and analysis
5.1 Performance test of K-DSA

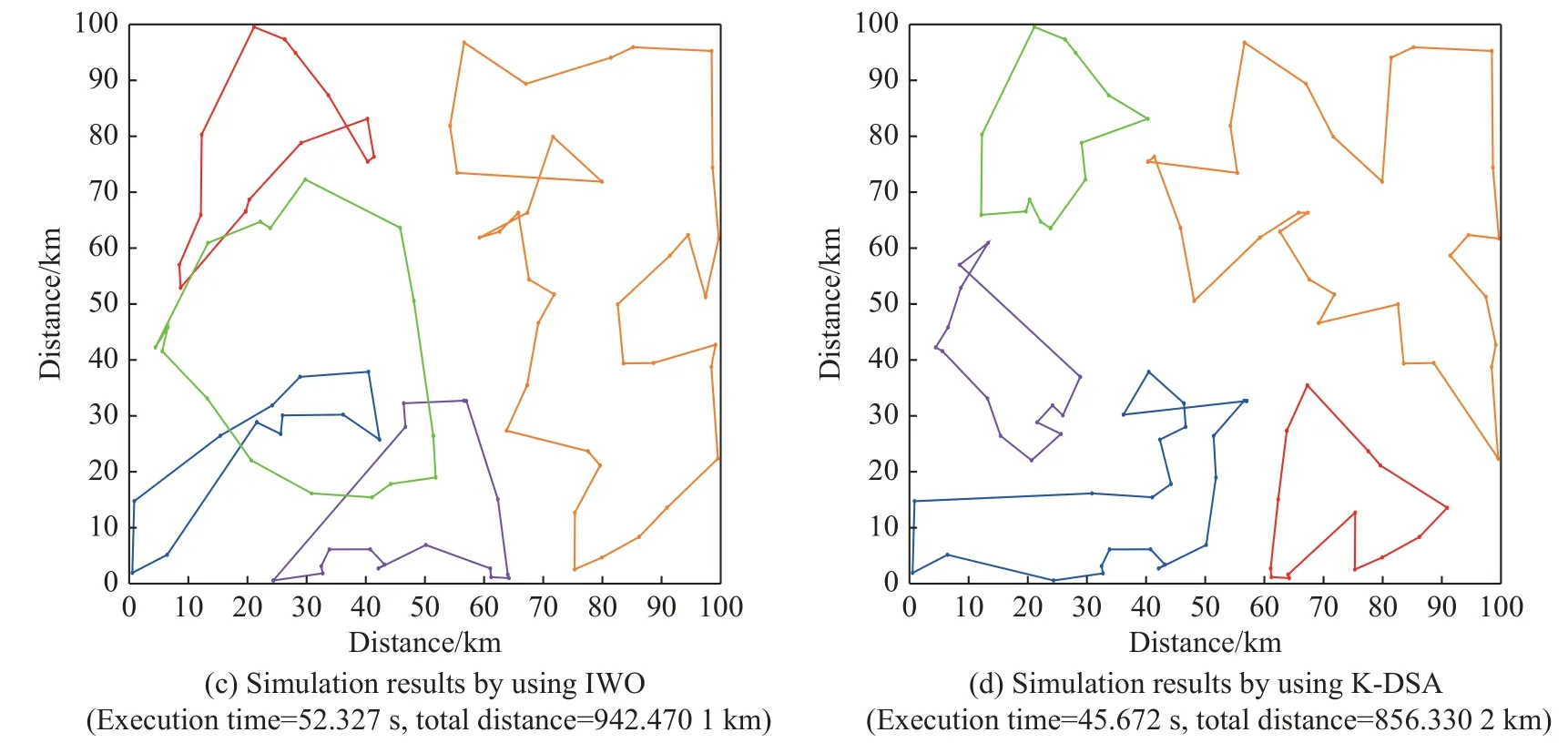
5.2 Comparison with other algorithms

6.Conclusions
杂志排行
Journal of Systems Engineering and Electronics的其它文章
- Two-layer formation-containment fault-tolerant control of fixed-wing UAV swarm for dynamic target tracking
- Role-based Bayesian decision framework for autonomous unmanned systems
- Nonlinear direct data-driven control for UAV formation flight system
- Minimum-energy leader-following formation of distributed multiagent systems with communication constraints
- A survey on joint-operation application for unmanned swarm formations under a complex confrontation environment
- Multicriteria game approach to air-to-air combat tactical decisions for multiple UAVs
