Uncertainty entropy-based exploratory evaluation method and its applications on missile effectiveness evaluation
2024-01-17HUJianwenWANGZhihuiGAOYuanZHUXiaominTIANYongliangandLIUHu
HU Jianwen, WANG Zhihui,2,*, GAO Yuan, ZHU Xiaomin, TIAN Yongliang, and LIU Hu
1.Consulting Center for Strategic Assessment, Academy of Military Science, Beijing 100097, China;2.Army Academy of Artillery and Air Defense (Nanjing Campus), Nanjing 211132, China;3.School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China;4.College of Systems Engineering, National University of Defense Technology, Changsha 410072, China
Abstract: Some attributes are uncertain for evaluation work because of incomplete or limited information and knowledge.It leads to uncertainty in evaluation results.To that end, an evaluation method, uncertainty entropy-based exploratory evaluation(UEEE), is proposed to guide the evaluation activities, which can iteratively and gradually reduce uncertainty in evaluation results.Uncertainty entropy (UE) is proposed to measure the extent of uncertainty.First, the belief degree distributions are assumed to characterize the uncertainty in attributes.Then the belief degree distribution of the evaluation result can be calculated by using uncertainty theory.The obtained result is then checked based on UE to see if it could meet the requirements of decision-making.If its uncertainty level is high, more information needs to be introduced to reduce uncertainty.An algorithm based on the UE is proposed to find which attribute can mostly affect the uncertainty in results.Thus, efforts can be invested in key attribute(s),and the evaluation results can be updated accordingly.This update should be repeated until the evaluation result meets the requirements.Finally, as a case study, the effectiveness of ballistic missiles with uncertain attributes is evaluated by UEEE.The evaluation results show that the target is believed to be destroyed.
Keywords: uncertainty entropy-based exploratory evaluation(UEEE), evaluation activity, belief degree distribution, missile effectiveness.
1.Introduction
The basic goal of evaluation activities is to obtain a “net”assessment [1], which means the uncertainty in the evaluation should be reduced to obtain a clear and elegant result.However, the evaluation problems are usually fraught with uncertainties (unknowns) which perplex the whole evaluation process.
In practice, a net assessment is usually hard to be obtained.On the one hand, the evaluation object’s attributes are uncertain; on the other hand, the relationship between the evaluation object’s attributes and the evaluation results is also uncertain.For example, determining the attribute values of an air-surface missile in a complex operational environment can be difficult and expensive.In addition, it is hard to determine the performances of enemy air defense weapon systems.Moreover,it is difficult to generate the relationship between the missile’s operational effectiveness and capability parameters.As a result, calculating the “net effectiveness” of the missile in the operational context is difficult and rarely reported in literature.
Though uncertainty leads to the difficulties in achieving net assessment, it is still common in evaluations.Cheng et al.identified the performance parameters and corresponding weights of the attack helicopter using a qualitative-to-quantitative transformation of the linguistic variable [2].Then the analytic hierarchy process(AHP) is used to calculate the system effectiveness of the attack helicopter.Luo et al.used interval numbers to characterize uncertainty in attributes [3].The uncertain results were described by intervals.The ranking result of alternatives was calculated based on the ranking method proposed in [4,5].Wu et al.used interval numbers with probability distribution to characterize uncertainty [6-8].Then the ranking results were obtained by the mean-variance method, the mid-point and half-width method, and other algorithms.Bandte et al.used the subjective probability distribution approach to characterize the uncertainty of attributes [9-11].They then calculate the probability distribution of the evaluation result based on the experiment model (e.g., simulation model), or aggregate operators (e.g., weighted average operator, weighted geometric operator).Finally, the mean or other statistic is used to represent the evaluation result.In addition, fuzzy sets [12,13], fuzzy variables [14], rough sets [15], and other mathematical tools are used to characterize uncertainty in evaluation.The outcome of the evaluation is still presented as a statistical value, like a mathematical expectation.
For the existing evaluation methods with uncertainty,two issues have not been well studied:
(i) Mathematical tools for characterizing human uncertainty.Uncertain attributes are traditionally characterized by subjective probability distributions [16,17] or interval numbers [18,19].In that case, the extent of uncertainty is measured by variance [20-22] or the length of the interval [18,19].However, this probabilistic form with associated operational rules is usually only suitable for random cases with enough samples.Liu pointed out that probability theory is no longer applicable when the estimated probability distribution is not close enough to the inherent frequency [23,24].This is because, in the absence of many samples, estimating the inherent frequency is typically difficult.Furthermore, using fuzzy variables to describe attribute uncertainty may result in a logical paradox as discussed in [23].
(ii) Treatment of uncertain results.The evaluation results need to be used to compare which alternative is better, so uncertain results are usually replaced with certain values.Traditional methods, such as methods in[25-28], mainly rely on statistic values (e.g., expectation,maximum value).In practice, however, the statistical values often differ from the actual values, as discussed in the example of fighter jet seat design in [29].To achieve an accurate and comprehensive evaluation result, reducing uncertainty in results should be conducted, rather than simply replacing uncertain results with a statistical value.
Evaluation methods, which can measure uncertainty and gradually reduce uncertainty in practice, are rarely reported in literature.Reducing the uncertainty should be essential to the evaluation works, otherwise the evaluation results would not be trustworthy.For example, in the development of equipment (e.g., a missile), it is necessary to evaluate the operational effectiveness of various design options with uncertainty reduced (especially in the initial design phase).Only in this manner, the net effectiveness of each design option can be determined to support equipment research and development.This is the main motivation for the works performed in this paper.
In this paper, we propose a new systematized evaluation method to reduce the uncertainty in a complex problem, which gets rid of calculating statistic values.This method is called uncertainty entropy-based exploratory evaluation (UEEE).It is based on an iterative approximation process.In this method, the belief degree distribution function [30] is introduced, which is appropriate for intuitive judgement to characterize the uncertainty in evaluation work [23,30].Based on it, the uncertainty entropy (UE) is proposed to measure the extent of uncertainty.Furthermore, an analytical model is proposed to calculate the contribution of each attribute to overall uncertainty of the evaluation result.Based on that, reducing the uncertainty of the evaluation result can be achieved by iteratively reducing the uncertainty of the attributes with large contributions.
This paper is organized as follows: Section 2 presents the fundamentals of belief degree distribution.Section 3 proposes the evaluation method (UEEE).Section 4 applies UEEE in evaluating ballistic missile operational effectiveness under uncertainty.Section 5 concludes the paper.
2.Fundamentals of belief degree distribution
2.1 Uncertainty characterization
In general, uncertainty can be classified into two categories: aleatory uncertainty and epistemic uncertainty[31-33].
Aleatory uncertainty is referred as the uncertainty inherent in the physical behavior of the system.It is usually considered irreducible and is expressed in terms of probability (long-run frequency).For example, there is no way to reduce the uncertainty of the outcome of a dice roll or a coin toss.
Epistemic uncertainty is categorized as uncertainty caused by incomplete knowledge or limited information.This type of uncertainty can be reduced.More precise measurements or more experiments can help reduce epistemic uncertainty.However, it usually needs a great investment of manpower, materials, cost and time.
Therefore, the goal of UEEE here is to efficiently reduce epistemic uncertainty in evaluation results.Some researchers have used subjective probability to quantify epistemic uncertainty [34-36].However, as discussed in[23,24], a fundamental premise of applying probability theory is that the estimated probability is close to the longrun frequency, otherwise, using subjective probability may result in errors.
Belief degree indicates the strength of a person’s belief that an event will occur.Belief degree takes values between 0 and 1.The higher the value, the higher the probability that the person subjectively feels that the event will happen.From an axiomatic point of view, the essential difference between probability and belief degree is the difference in the product degree.Roughly speaking,the product measure of probability theory is “multiplication”, while the product measure of belief degree is “taking the smallest”, i.e.,
wherePris the probability measure,Mis the belief degree measure.Give an example to look at how subjective probability differs from belief degree.A specific exam has four subjects (math, politics, history, and geography), and one person must pass all four to pass the exam.Assume a person takes the exam and he believes there is a possibility of 70% that he can pass math, 70%that he can pass politics, 70% that he can pass history,and 50% that he can pass geography.If the chance of passing the exam is calculated by using the probability theory, the probability of passing the exam can be calculated as 0.7×0.7×0.7×0.5 ≈0.17.By applying uncertainty theory instead, the belief degree of passing the exam can be calculated as 0.7∧0.7∧0.7∧0.5=0.5.Clearly, the person is just very unsure about passing the geography subject (0.5 belief degree), which cannot indicate that he believes that he will fail, nor that his chance of passing is slim.If there are more subjects, the probability of passing this exam could be close to 0.Therefore,the result obtained by subjective probability seems unreasonable.
Everyone approaches the same problem from a different angle.However, subjective probability does not correspond to the characteristics of human intuitive thinking.For this reason, the long-run frequency of an event is difficult to estimate.Long-run frequency imagination is far more difficult than natural feeling.Thus, the unknown attributes are hardly precisely described by probability distributions.However, applying probability theory requires precise distributions because the probability multiplication rule could amplify errors, resulting in incorrect decision-making.In contrast, the minimum rule of belief degree would be more reliable.As a result, we think subjective probability is useful when an expert with reasonably reliable information and a precise opinion is available.Otherwise, belief degree distribution is more reliable.That’s why, in this study, only the belief degree is used to measure the attribute uncertainty.
Some attributes, such as the circular error probability(CEP) of an unknown missile, cannot be determined precisely; thus, the support of domain experts is needed to evaluate the belief degree distribution of attributes in a certain range.One possible way of modeling the belief degree is to use a fuzzy membership function [14,37].However, it is usually inappropriate because it may lead to counter-intuitive results.In [23,38], an example of the bridge overload is provided to explain the reasons.The characterization of the attribute “overload” should use a belief degree distribution rather than frequency due to the information reliability.Since the uncertainty stems primarily from the limitations of the measurement facility,we cannot obtain the precise/reliable value of “overload”.The uncertainty distribution function of “overload” is given in Fig.1.
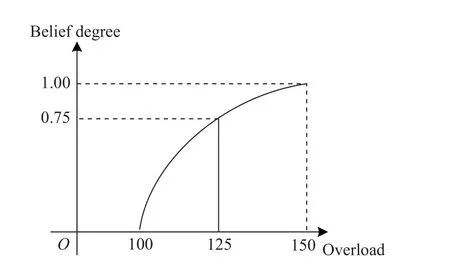
Fig.1 Uncertainty distribution function of overload
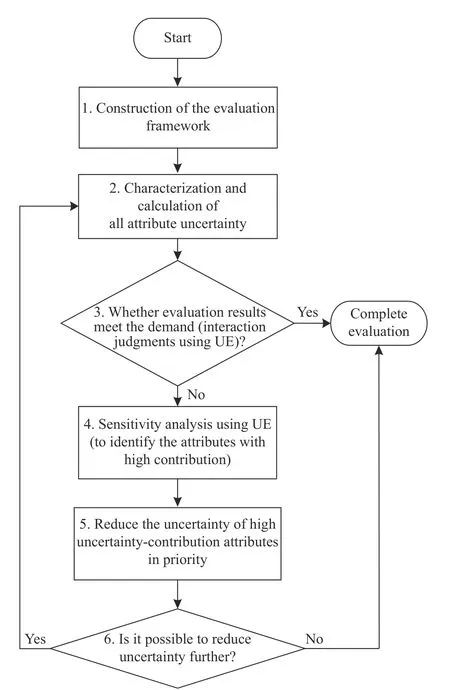
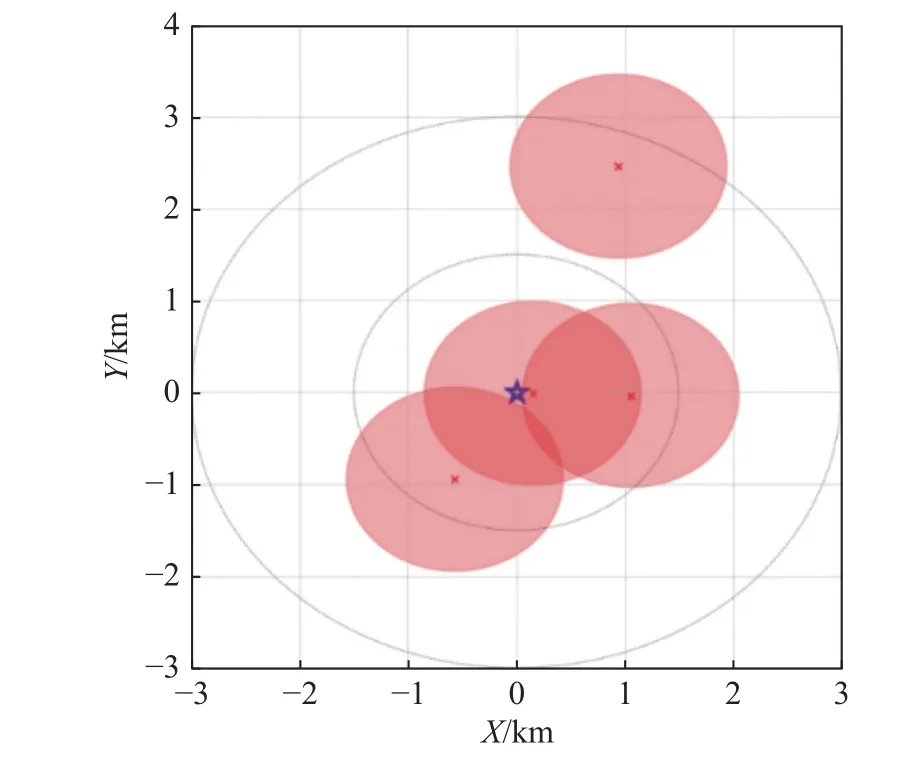
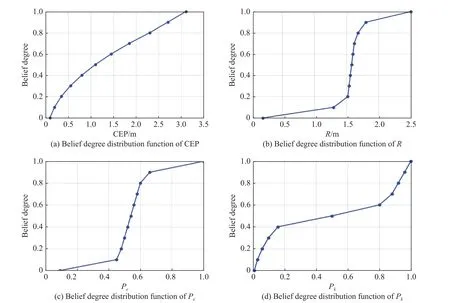
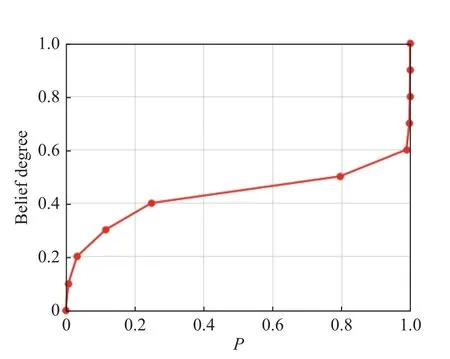
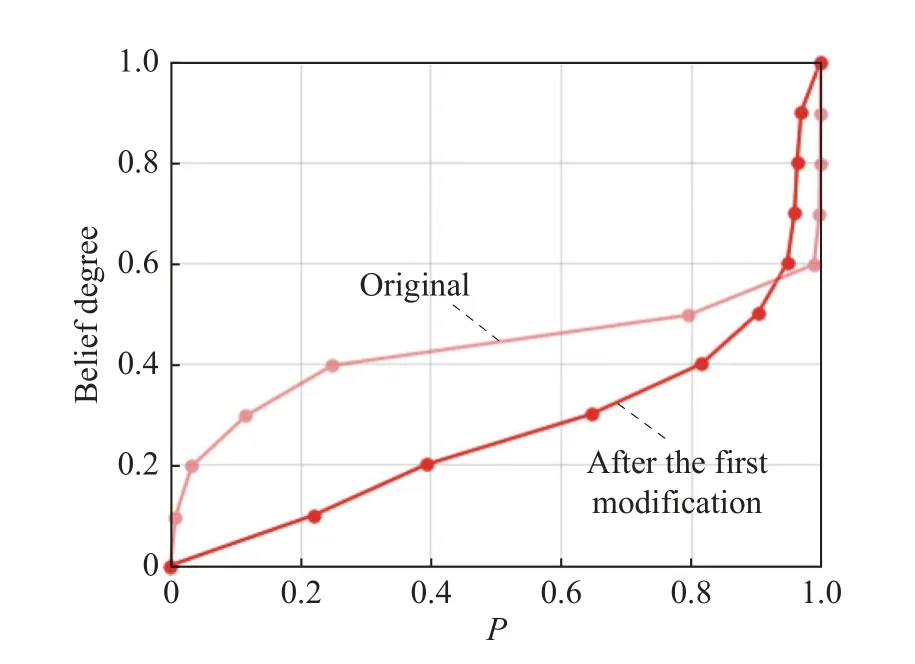
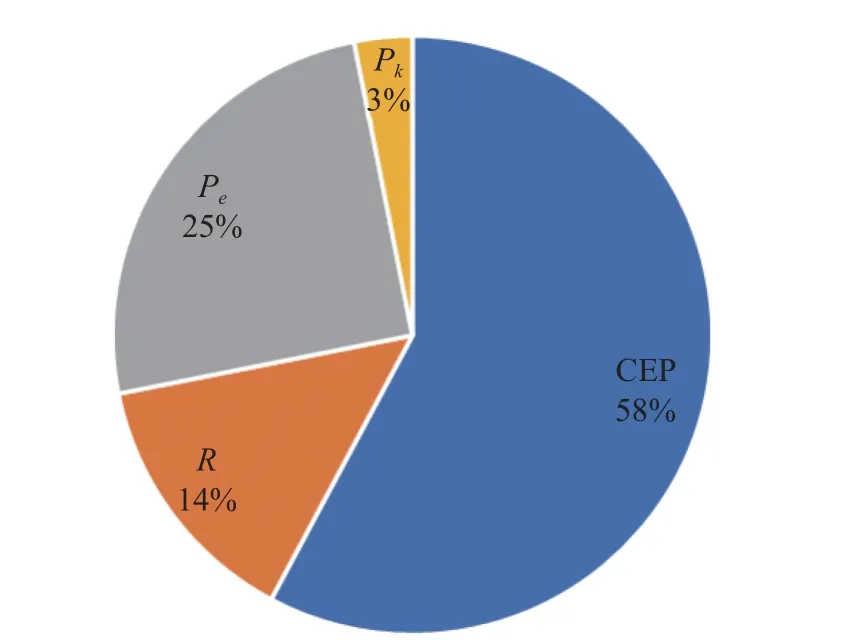
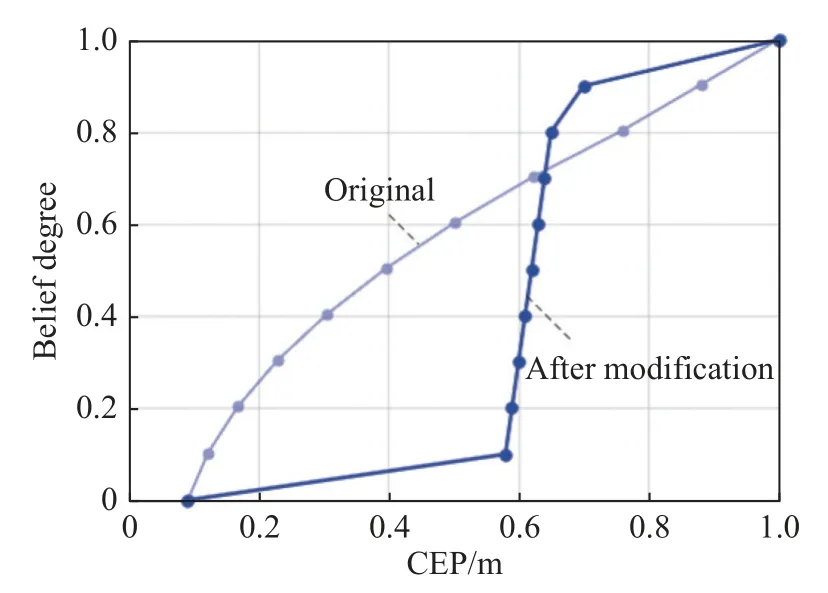
The belief degree measureM(γ) represents the happening belief degree of the eventγ.For example,M(overload < 100) represents the belief degree of the uncertain attribute “overload” is smaller than 100.The uncertainty distribution functionΦ(y) means the belief degree of the uncertain attributex for any given vectorY[30]. The above is the basic principle of the belief degree distribution.It is applicable mainly when there are not enough samples (even no sample) to evaluate a probability distribution.In that case, the generation of the belief degree distribution function relies mainly on the subjective human judgment.The specific process is as follows:First, the expert uses a calibration method, which can be referred as in [39], to perform a calibration exercise.Interaction with experts is then used to collect evaluation data.Finally, the belief degree distribution function is generated by using the segmental interpolation method.The detailed steps can be found in [38,40]. Definition 1[30] A belief degree distribution functionΦ(x) is regular when it is a continuous and strictly increasing function with respect tox, at which 0 <Φ(x) <1, and A regular uncertainty distribution functionΦ(x) has an inverse function on the range ofxwith 0 <Φ(x) < 1, and the inverse functionΦ-1(α) exists on the open interval(0,1). Definition 2[30] Assumeξis a variable with a regular belief degree distribution functionΦ(x).The inverse functionΦ-1(α) is then referred to as the inverse function of the belief degree distribution ofξ. Definition 3[30] The uncertain variablesξ1,ξ2,···,ξnare assumed to be independent if Similarly, after transforming, iffis a strictly decreasing function, then As discussed, the goal of UEEE is to reduce uncertainty in evaluation results and make them more certain.The extent of uncertainty in an evaluation result is primarily determined by the uncertainty in the attributes and their sensitivity to the evaluation result.Regions with high sensitivity and uncertainty are referred to as “extreme states”in [41], and they have a significant impact on the desired evaluation results. Since the sensitivity of attributes is inherent to the evaluation model, it cannot be reduced.Therefore, the uncertainty in evaluation results can only be reduced iteratively by reducing the attribute uncertainty.However,reducing the uncertainty in all attributes is impractical in most practical problems due to the limited resources,time, and cost.As a result, the key attribute(s) should be first found which can mostly affect the uncertainty of the evaluation result. Fig.2 shows the general process of the proposed UEEE.The method is using UE to measure the extent of uncertainty.First, an evaluation framework is constructed, which consists of evaluation indicators, evaluation object attributes, and evaluation models.Following that, all uncertain attributes are characterized with belief degree distributions.The belief degree distribution of the evaluation result is then calculated based on uncertainty theory [38].The belief degree distribution of the result is then checked based on UE to see if it could support decision-making. Fig.2 Procedures of UEEE If the level of uncertainty in the result is too high, more information and knowledge need to be introduced, for example, conducting more experiments.Then the uncertainty in attributes can be reduced.The sensitivity analysis is performed based on UE to find which attribute(s)mostly contributes to the uncertainty of the evaluation result.Thus, efforts can be made to reduce uncertainty in the obtained key attribute(s) by investing in both human and material resources.The belief degree distribution of the evaluation result is updated with the modified attribute(s).The preceding procedures need to be carried out iteratively until the UE of the evaluation result meets the requirements. The evaluation framework mainly consists of evaluation object attributes, evaluation results and the evaluation models. Evaluation object attributes (abbreviated as attributes in this paper) are the inherent nature of a system.Attributes represent a system’s essential characteristics.Attributes may be certain or uncertain.Uncertain attributes are very common in the evaluation of practical complex problems.The evaluation result is a set of quantitative scales defined according to the evaluation objective.The evaluation model is the mapping relationship between attributes and the evaluation result.The type of an evaluation model could be an analytical model, a numerical model, a simulation model, a physical experiment model, or a subjective judgment model. An evaluation model can be expressed as the mapping function below: whereYis the evaluation result,Xis the vector of attributes, andis the uncertain value.f(·) is the evaluation model.It is worth noting that the evaluation model functionf(·) can be assumed to be monotonic [42,43] in the most evaluation practices. When evaluating a complex problem, the evaluation object attributesX, as well as the evaluation modelf(·),are usually uncertain for humans.Therefore, the evaluation resultYis also uncertain.The goal of UEEE is to reduce epistemic uncertainty inY.It could be achieved by reducing the uncertainty of high uncertainty-contribution attributes iteratively. Information entropy is widely used in information theory to express the expectation of the amount of information about a random event.Probability theory has information entropy, and belief degree theory should also have the concept of entropy.This section gives the definition of UE on the basis of the principle of the belief degree distribution function. Definition 4 UE is used to measure the extent of uncertainty of an uncertain variable.Let ξ be an uncertain continuous variable with a belief degree distribution function of Φ, corresponding to the UE: The Sobol method is built on the basis of probability theory.The reason for its computational complexity is closely related to the fact that its first nature principle is probability theory.In probability theory, the calculation of probability distributions of multiple independent variables is very complicated.For example, the result of adding two independent random variables needs to be expressed in terms of convolution.The addition ofnindependent random variables will produce ann-1 dimensional convolution equation, that is,n-1 reintegration, and this calculation can only rely on Monte Carlo methods, which are computationally intensive.From a pragmatic point of view, UE is more advantageous.Using the belief degree distribution function to portray the uncertainty is more consistent with human intuitive thinking, and the calculation is simpler.□ Based on the calculation of the contribution ratio, the attributes with the high contribution should be prioritized for the following uncertainty reduction.New knowledge and information need to be introduced.Activities such as conducting more experiments or precise measurements need to be implemented.Then the distributions of key attributes can be modified.The wisdom of crowds [44],which involves the collaboration of multiple experts, is another important method for reducing uncertainty [40].The accuracy of subjective judgment depends not only on one’s knowledge and experience, but also on one’s character and state.Being too confident or too conservative can have an impact on the accuracy of judgment.In order to improve the accuracy of expert judgment and reduce judgment noise, experts need to be calibrated before they give judgment data.The calibration method can be found in [40].In addition, the Delphi method and multi-expert belief degree integrated method [40] can help reduce judgment noise. If the uncertainty of an attribute is hard to reduce, the attributeXican also be regarded as an indicatorY.Then a similar approach can be used again.It means a difficult problem can be decomposed over and over again.That is to say, UEEE can be used recursively.The evaluation results’ uncertainty is reduced iteratively and recursively by applying UEEE. Mission scenario: There are six ballistic missiles attacking the enemy military target (such as a command center).The operation objective is to damage the target(to make it lose operational capability).The commander needs to decide whether to launch the studied missiles.The main concern is, the location of our missiles can be discovered once the attack is launched.It means that once the missiles are launched, the target must be destroyed;otherwise, the enemy can counterattack, resulting in a passive situation.Therefore, the operational effectiveness of the six ballistic missiles needs to be evaluated in terms of the probability of destroying the enemy target. The main factors influencing ballistic missile operational effectiveness are the number of missilesN, the penetration probability of missiles launchedPe, the circular probability error CEP, the damage radiusRof a single missile, and the probability of a single missile damaging the targetPk.They are all considered in the following evaluation works. Evaluation result: the damage probabilityPof the target losing operational capability. Evaluation object attributes: the number of ballistic missilesN, the penetration probability of missiles launchedPe, circular probability error CEP and damage radiusR, damage probability of a single missilePk. Evaluation model:P=f(N,CEP,R,Pe,Pk) , wherefis the simulation experiment in this case study. The simulation experiment model is built, whose principles are shown in Fig.3.Nmissiles are launched.Use random simulation to choose which missiles penetrate successfully.Next, calculate the position of each missile drop point according to CEP.Determine the damage circle according to the damage radius.Then count the number of damage circles that contain the target, lettbe the number.The damage probabilityPof the target losing operational capability can be calculated by using the following equation: Fig.3 Process of the simulation Fig.4 shows the results of a randomized simulation experiment with six ballistic missiles striking the target.The experimental parameters are set asN= 6, CEP = 1 km,R=1 km,Pe= 0.8,Pk=0.6.Fig.4 shows that there are four missiles successfully penetrated and one missile hits the target with a damage probability of 0.6. After 5 000 simulations, the probability (long-run frequency) of the target being destroyed is convergent at 0.57.This result can be regarded as the evaluation result of the operational effectiveness of the six ballistic missiles with determined attributes. However, in practice, the above attributes (CEP,R,Pe,Pk) are difficult to obtain accurately.It means that they are uncertain.Domain experts need to be added to evaluate their belief degree distributions. Fig.4 Simulation of the target attacked by six ballistic missiles The belief degree distributions of uncertain attributes(CEP,R,Pe,Pk) are generated as shown in Fig.5. From Fig.5,Pkis highly uncertain because its belief degree is concentrated around 0.5. Fig.5 Belief degree distributions of uncertain attributes In the simulation experimental model, the functional relationships amongR,Pe,Pk, andPcan be regarded as increasing functions in their ranges, whereas the functional relationship between CEP andPcan be regarded as a decreasing function in their ranges.According to Theorem 1, (4) and (5), that is, By using (15), the belief degree distribution function ofPis calculated as shown in Fig.6. Fig.6 shows that the belief degree ofP< 0.99 is 0.6.The belief degree ofP>0.99 is 0.4, which means the target could be damaged successfully by missiles with a 40% belief degree.It is uncertain for humans to give a decision.The epistemic uncertainty ofPshould be reduced. Fig.6 Belief degree distribution of P As mentioned, the exploratory evaluation method reduces the UE of the evaluation result by iteratively reducing the UE of high uncertainty-contribution attribute in priority. By using (8), the UE of evaluation resultPcan be given as 0.97. Then, use (9), the obtained UE of CEP,R,Pe,Pkis 2.15, 0.83, 0.83, 0.83, respectively. By using (12) and (13), the contribution of each input parameter to the uncertainty inPis calculated by using the numerical approach: CEP contributes 0.21,Rcontributes 0.03,Pecontributes 0.04, andPkcontributes 0.70.The summation of CEP,R,Pe,Pkis 0.98.It approximately equals the uncertain entropy ofP(SP=0.97),indicating that the calculation is correct.The contribution ratio of each input parameter is shown in Fig.7. Fig.7 Each attribute’s contribution ratio After finding the most important attributePk, the next step is to invest both human and material resources to reduce the uncertainty inPk.The belief degree distribution function ofPkis modified as shown in Fig.8.At this point, the UE ofPkdecreases from 0.83 to 0.30 by using (9). Fig.8 Belief degree distribution of Pk after modification Similar to the above steps, re-evaluatePafter the first round of modification.The new belief degree distribution function ofPupdates as displayed in Fig.9.At this point, the UE ofPdecreases from 0.97 to 0.65 by using(8).It is obvious that uncertainty has been greatly reduced.However, the uncertainty inPstill remains so high that we are unable to draw conclusions that they can be used to support decision-making.Instead, we need to continue to reduce the uncertainty of the key attributes. Fig.9 Belief degree distribution of P after the first modification The contribution of each input parameter to the uncertainty inPis updated: CEP contributes 0.37,Rcontributes 0.09,Pecontributes 0.16, andPkcontributes 0.02.The summation is 0.64.It approximately equals the uncertain entropy ofP(P=0.65), indicating that the calculation is correct.The new contribution ratio of each input attribute after the first modification is shown in Fig.10. Fig.10 Each attribute’s contribution ratio after the first modification At this point, both human and material resources are needed to reduce the uncertainty in CEP.The belief degree distribution function of CEP is modified as shown in Fig.10.As a result, the UE ofPkdecreases from 2.15 to 0.46. Re-evaluatePafter the second round of modification.The new belief degree distribution function ofPis updated again (Fig.11).At this point, the UE ofPdecreases from 0.65 to 0.32.It is apparent that the effect of reducing uncertainty is also beneficial. Fig.11 Belief degree distribution of CEP after modification As seen in Fig.12, the belief degree ofP< 0.8 is 0.1.That is to say, the belief degree ofP> 0.8 is 0.9, which means that the probability (long-run frequency) of the target destroyed by six missiles (with 90% belief degree)exceeds 0.8.Therefore, the commander has a high level of confidence to launch the attack. Fig.12 Belief degree distribution of P after the second modification From the evaluation result, it is clear that the belief degree distribution is a more reasonable mathematical tool for modeling epistemic uncertainty than subjective probability.It may be confusing to describe the unknown damage probability with a subjective probability distribution. From the case study of multiple missiles, when all evaluation attributes are determined, we can calculate the inherent probability (long-run frequency) of the target being destroyed through many experiments.However, these attributes are uncertain.It is difficult for us to measure them precisely, and we do not have enough samples (or even no sample) to estimate probability distributions. In this study, domain experts are invested to evaluate their belief degree distributions.Then the belief degree distribution of the evaluation result can be calculated by using uncertainty theory.The evaluation result is then checked based on UE to see if it could satisfy the requirement of decision-making.If the requirement is satisfied,the evaluation work can be finished.If not, a sensitivity analysis is performed to identify the key attribute that contributes the most to the UE of the evaluation result.For the key attribute, human and material resources are invested to introduce new information in order to reduce their uncertainty.Then the belief degree distribution of the key attribute can be modified.Following that, the belief distribution of the evaluation result can be updated with the modified attribute.The iterative reduction is repeated until the UE of the evaluation result meets the requirements.Finally, a reliable evaluation result that can support decision-making is obtained. The UEEE method is proposed in this paper, which employs an iterative approximation process.The method gives specific steps to reduce the uncertainty in evaluation results in order to improve the reliability of the results.It has the following advantages: (i) UEEE uses an exploratory iterative approach to gradually reduce uncertainty in evaluation results, rather than simply using statical values such as expectation, as the ultimate evaluation (or assessment) result. (ii) UE can better quantify the extent of epistemic uncertainty than variance.It corresponds more to human intuitive thinking than variance. (iii) An analytical model for UE contribution analysis is proposed, which provides an important tool for identifying the key attribute(s) that mostly affects the uncertainty of the result.UE is easy to calculate and suitable for high-dimensional space.Thus, it can be directly applied to the evaluation activities, especially those with limited resources to reduce the uncertainty in attributes.In this way, the efficiency of evaluation work can be improved.2.2 Operation of belief degree distribution function

3.Proposed UEEE
3.1 Principles and procedures of UEEE
3.2 Construction of evaluation framework
3.3 Uncertainty metric and uncertainty contribution analysis of attributes




3.4 Reducing the uncertainty of high uncertaintycontribution attributes
4.Illustrative example: evaluation of ballistic missile operational effectiveness under uncertainty
4.1 Evaluation framework

4.2 Attribute belief degree distributions and evaluation results

4.3 Reducing UE of evaluation results iteratively


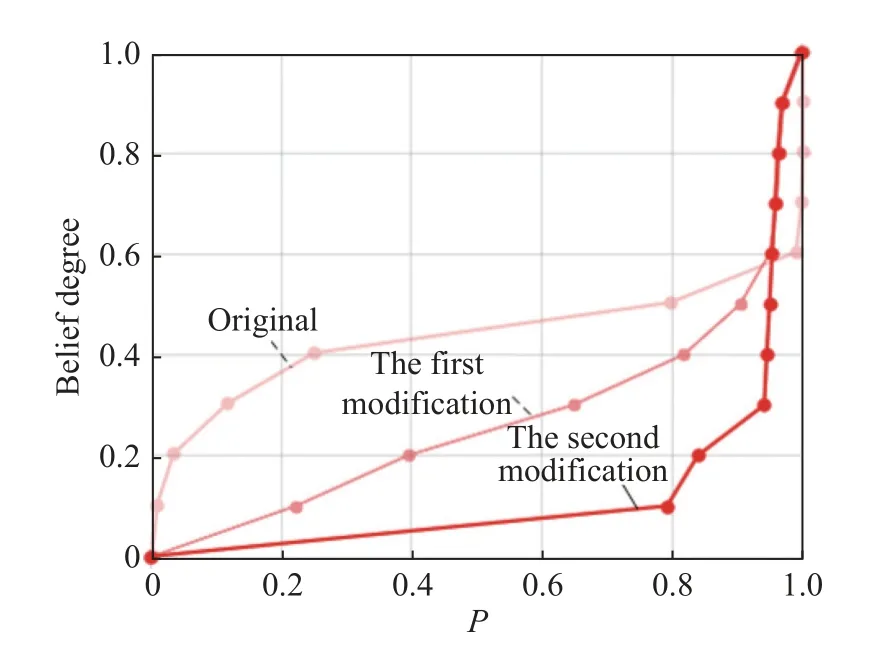
4.4 Discussions
5.Conclusions
杂志排行
Journal of Systems Engineering and Electronics的其它文章
- Support vector regression-based operational effectiveness evaluation approach to reconnaissance satellite system
- K-DSA for the multiple traveling salesman problem
- Formal management-specifying approach for model-based safety assessment
- Consensus model of social network group decision-making based on trust relationship among experts and expert reliability
- A cooperative detection game: UAV swarm vs.one fast intruder
- Complex task planning method of space-aeronautics cooperative observation based on multi-layer interaction
