基于q轴阻抗重塑的并网逆变器稳定控制策略研究

摘 要：随着可再生能源装机容量的增加，电网呈现出大电网阻抗的弱电网特性。通常逆变器通常通过锁相环（phaselocked loop，PLL）获得电网同步信息，为了抑制电网电压的背景谐波和幅值干扰，还需要进行电网电压前馈（grid voltage feedforward，GVF）控制。PLL和GVF引入的负面效应将导致逆变器在弱电网下不稳定。因此，本文提出了一个阻抗控制器，用于在低频段将q轴阻抗重塑为正电阻，解决了PLL和GVF造成的系统不稳定问题。

关键词：电网阻抗；电压前馈；锁相环

中图分类号：TM464  文献标识码：A

Abstract：With the increasing installed capacity of renewable energy，the gridpresents characteristics of weak grids with large grid impedance.In general，the inverter often obtains grid synchronization information by the phaselocked loop（PLL）and to suppress thebackground harmonic and amplitude disturbance of grid voltage.the grid voltage feedforward（GVF）control is also needed.The negative effects introduced by PLL and GVF will cause the inverter to be unstable under the weak power grid.Therefore，this paper proposes an impedance controller for reshaping the qaxis impedance to positive resistance in the low frequency band，solving the problem of system instability caused by PLL and GVF.

Keywords：Grid impedance；grid voltage feedforward（GVF）；phaselocked loop（PLL）

隨着分布式发电系统的不断普及，分布式发电系统的位置分散，长距离输电线路以及大量变压装置使得电网呈现较高的阻抗，表现为弱电网特性。在弱电网下，并网逆变器的稳定性会受到电网阻抗的严重影响。一般来说，并网逆变器通常通过锁相环获得准确的电网同步信息，而为了抑制电网电压背景谐波，提高电流控制动态性能，还需要进行电网电压前馈（GVF）控制。然而，已有的研究发现，PLL和GVF会将逆变器的q轴输出阻抗塑造成一个负电阻，造成了逆变器在弱电网条件下的不稳定。因此，本文提出了一种通过q轴阻抗重塑的并网逆变器稳定性控制策略，从而提高了系统的稳定性。

1 带PLL和GVF的并网逆变器的建模

本节将依次对PLL、GVF建模以得到并网逆变器的整体小信号模型，为后面的稳定性分析提供基础。

1.1 并网逆变器的主电路拓扑结构

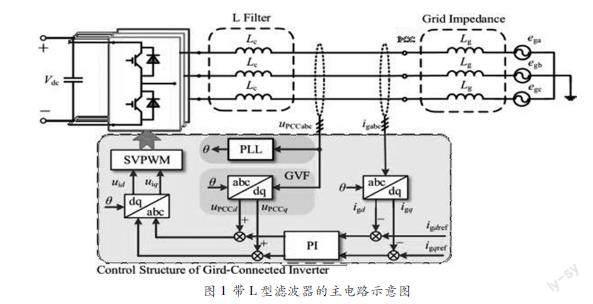
图1是以L型滤波器为研究对象的三相并网逆变器及其典型的主电路拓扑结构，其中Vdc为直流电压，Lc为逆变器滤波电感，ig为电网电流，egabc代表电网电压。Igdref和igqref分别为d轴和q轴电网电流的参考值。Igd和igq是ig在同步dq坐标系中的d轴和q轴分量。θ是PLL根据PCC电压uPCCabc得到的相位。UPCCd和uPCCq是uPCCabc在同步dq坐标系中的d轴和q轴分量。本文只分析了电网阻抗的电感分量Lg，它决定了并网逆变器的稳定性。

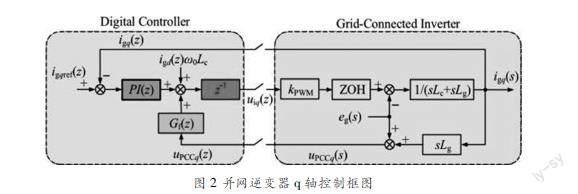
对并网逆变器的q轴输出阻抗进行建模，带有数字控制器的并网逆变器的q轴控制框图如图2。

比例积分（PI）控制器通常被用于电流调节器。PI控制器的离散化策略是Tustin变换，它给出了转移等效的离散时间电流控制器的函数为：

PI（z）=KP+Kl+Gint（z）（1）

其中KP和KI分别是PI控制器的比例系数和积分系数。Gint（z）代表一个离散的积分器，其表达式为：

Gint（z）=Ts2（z+1）（z－1）（2）

其中，Ts是逆变器的采样周期。

1.2 PLL的建模

PLL的输出闭环传递函数：

GPLL（z）=Δθ（z）ΔuPCCq（z）=GPLL_PI（z）Gint（z）1+GPLL_PI（z）Gint（z）UPCCd（3）

其中θ表示PLL的输出角度，GPLL_PI（z）表示PLL的PI调节器，其表达式为：

GPLLPI（z）=KPLLP+KPLLIGint（z）（4）

其中KPLL_P和KPLL_I分别是GPLL_PI（z）的比例系数和积分系数。UPCCd表示d轴PCC电压的幅值。

1.3 GVF的建模

GVF的小信号模型：PCC电压通过GVF传输后，其d轴和q轴电压分量经历了PLL的角度变换。因此：

ΔuPCCd_PLL（z）

ΔuPCCq_PLL（z）=1－UiqGPLL（z）

0Gf（z）［1－UPCCdGPLL（z）］ΔuPCCd（z）

ΔuPCCq（z）

=HVPLLΔuPCCd（z）

ΔuPCCq（z）（5）

其中HVPLL是小信号扰动的矩阵模型。

ΔuPCCd_PLL（z）和ΔuPCCq_PLL（z）分别代表PCC电压在PLL dq坐标系中的d轴和q轴。ΔuPCCd（z）和ΔuPCCq（z）分别代表PCC电压在逆变器dq坐标系中的d轴和q轴。

1.4 整体小信号模型

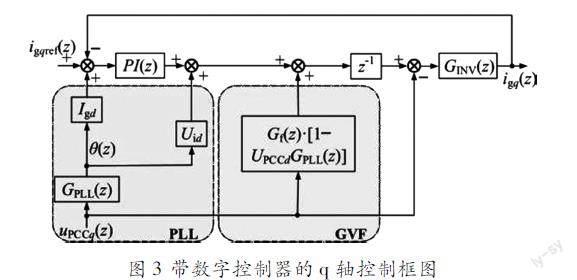
逆变器的整体q轴小信号模型如图3所示。在图3中，GINV（z）代表的是离散化模型。L型滤波的并网逆变器其表达式为：

GINV（z）=TsLc（z－1）（6）

逆变器的闭环传递函数可以表示如下：

Gcl（z）=igq（z）igqref（z）=z－1PI（z）GINV（z）1+z－1PI（z）GINV（z）（7）

因此，逆变器Yoq（z）的q轴输出导纳可由图3表示为：

Yoq（z）=1Zoq（z）

=－igq（z）uPCCq（z）

=Gcl（z）z－1PI（z）YINV（z）－Gcl（z）GPLL（z）Igd+UidPI（z）YINV（z）

－Gcl（z）PI（z）Gf（z）1－GPLL（z）UPCCdYGVF（z）

=YINV（z）+YPLL（z）+YGVF（z）（8）

其中YPLL（z）表示由PLL引入的q軸输出导纳，YGVF（z）表示由GVF引入的q轴输出导纳，YINV（z）表示不考虑PLL和GVF的逆变器输出导纳。

由（8）可知，YPLL（z）和YGVF（z）通过闭环传递函数GPLL（z）耦合，因此，PLL的PI参数值会影响PLL和引入逆变器的GVF的q轴输出阻抗，从而进一步扩大逆变器q轴输出阻抗在低频段的负阻区域，逆变器的稳定性将受到进一步影响。

2 拟定的稳定性控制策略

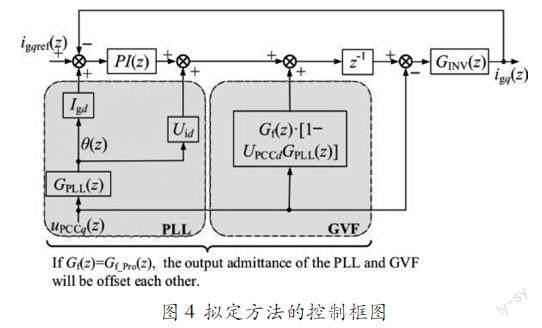
本文提出了一种考虑GVF的弱电网下变频系统的新型稳定性方案。该方案的原理是通过改变逆变器q轴电压前馈传递函数从Gf（z）到Gf_Pro（z）来抵消PLL和GVF的输出导纳，从而消除PLL和GVF引入的负电阻特性对逆变器稳定性的影响。图4展示了所提方法应用的原理框图。

首先，使PLL和GVF的输出导纳相互抵消，因此：

YPLL（z）+YGVF（z）=0（9）

将YPLL（z）和YGVF（z）代入（9）解得Gf_Pro（z）的表达式为：

Gf_Pro（z）=GPLL（z）IgdPI（z）+UidGPLL（z）UPCCd－1（10）

将式（1）、式（3）和式（4）代入式（10），Gf_Pro（z）可以进一步简化为：

Gfpro（z）=－IgdPI（z）+UidGPLLPI（z）Gint（z）

=－αGint（z）+βG2int（z）+γG3int（z）（11）

其中：

α=（KPIgd+Uid）KPLL_P

β=（KPIgd+Uid）KPLL_I+KIIgdKPLL_P

γ=KIIgdKPLL_I（12）

（12）中的参数可以分为两类：第一类是电流环的PI调节器和PLL的PI调节器的参数，它们是固定值；第二类是逆变器的工作点Igd和Uid，它们在运行过程中不断更新。事实上，Uid是d轴调制电压的幅值，它与Igd的值有关，并满足下列条件：

Uid= U2PCCd+（ω0LcIgd）2（13）

3 仿真验证

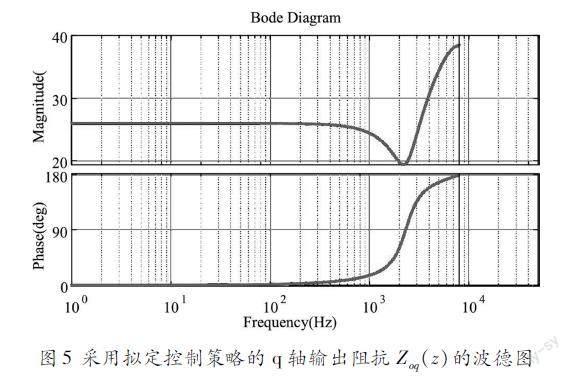
为了验证本文理论分析的正确性与所提控制策略的合理性，利用Matlab软件进行了仿真验证。得到了图5采用拟定控制策略的q轴输出阻抗Zoq（z）的波德图。从图5可以看出，逆变器q轴输出阻抗在低频段的负阻特性完全消失，说明所提出的控制策略消除了由PLL和GVF引入的不稳定特性。

结语

本文分析了弱电网下的并网逆变器的稳定性。结果发现，PLL和GVF带来了系统中的负阻区域。为了解决PLL和GVF造成的不稳定问题，本文提出了一种通过q轴阻抗重塑的并网逆变器稳定性控制策略，直接将q轴电压加到传输环节的q轴电流调节器输出，抵消了PLL和GVF对并网逆变器的输出阻抗的影响。最后，通过仿真验证了本文理论分析的正确性和所提控制策略的有效性。

参考文献：

［1］张烨，田慕琴，宋建成，等.弱电网下计及锁相环影响的并网逆变器输出阻抗重塑［J］.高电压技术，2021，47（11）：40334044.

［2］徐海亮，张伟杰，林鸿彬.一种提高并网逆变器无源性的阻抗重塑方法［J/OL］.电源学报，2022：115［20230506］.http：//kns.cnki.net/kcms/detail/12.1420.TM.2022090 8.1534.006.html.

［3］郭学迪.基于有源阻尼器的并网逆变器系统谐振抑制方法［D］.中国矿业大学，2022.

［4］高家元，肖凡，姜飞，等.弱电网下具有新型PLL结构的并网逆变器阻抗相位重塑控制［J］.中国电机工程学报，2020，40（20）：66826694.

作者简介：刘振武（1988— ），男，汉族，江苏徐州人，硕士，工程师，研究方向：电力系统自动化。