考虑硬故障与软故障的船用设备传感器可靠性评估

章文波，董从林，白秀琴

（1.武汉理工大学国家水运安全工程技术研究中心可靠性工程研究所，湖北武汉 430063；2.武汉理工大学船海与能源动力工程学院，湖北武汉 430063；3.武汉理工大学交通与物流工程学院，湖北武汉 430063）

当前，船用设备的运维可靠性水平是制约智能船舶发展的重要因素之一。为解决该问题，船舶行业提出了基于大数据驱动的船用设备智能运维技术[1]。船用设备传感器是获取运行状态大数据的重要装置，其可靠性决定了数据的完整性和准确性，严重影响智能化维修决策的正确性。对船用设备传感器的可靠性评估是其可靠性工作的重要内容。然而，由于船舶机舱内恶劣的环境条件，传感器承受各种各样的环境应力干扰，导致其故障模式多样、故障机理复杂，很难采用经典可靠性评估方法推测传感器的可靠性指标。另一方面，由于船舶行业内缺少可靠性数据共享机制，以及传感器在预防性维修工作中被提前维修或更换，使得可收集的传感器现场数据样本量较小，且充斥大量的删失数据，导致传感器的可靠性评估缺乏有效数据，难以保证精度。这些难点是船用设备传感器可靠性评估亟需解决的问题，但当前行业内还缺乏深入和系统的研究。

针对上述难点，本文将船用设备传感器的常见故障分类为硬故障和软故障2种，根据环境应力分析了其对应的故障机理，采用Weibull 分布作为硬故障的故障分布模型，采用逆高斯分布作为软故障的故障分布模型，进而根据竞争故障理论建立了故障模型和故障分布函数，并基于极大似然法给出了故障分布函数的参数估计方法。重点研究了故障占比较高的软故障，提出了融合现场数据和退化数据的可靠性评估方法。最后，以某压力传感器为算例对该方法进行验证。

1 船用设备传感器可靠性模型的建立

1.1 船用设备传感器的故障模式及对应故障机理

船用设备传感器是将外界被测量信息转化为电信号的装置，用于监测设备的运行状态参数，其工作环境恶劣，伴随着噪声、振动、高温、高湿、盐雾、油污等，导致其故障种类多样。常见的船用设备传感器故障有失灵故障、短路故障、断线故障、漂移故障、恒偏差故障等。根据故障的发生原因和维修措施，船用设备传感器的故障模式可以分类为硬故障和软故障[2]。硬故障是指船用设备传感器内部器件被永久性破坏导致的故障，一般通过更换传感器解决，主要表现为船用设备传感器无输出信号或间歇性输出信号，通常由电系统断路、短路或接触不良等原因引起。船用设备传感器的失灵故障、短路故障、断线故障均属于硬故障。软故障是指传感器内部器件性能参数变异导致的故障，可以通过调零校准等解决，主要表现为输出信号的误差超出允许范围，一般由电系统性能退化等原因引起。船用设备传感器的漂移故障、恒偏差故障均属于软故障。

故障是应力和强度相互作用的结果。根据应力的作用效果，可以将其分类为过应力和损伤应力。

过应力主要包括脉冲干扰应力、高温过应力和机械冲击应力。过应力的作用效果通常表现为船用设备传感器的内部元件或结构突然被破坏，传感器突然发生故障。显然，过应力是导致船用设备传感器硬故障的重要原因之一。

损伤应力主要包括电应力、稳态温度应力、温度循环应力、机械振动应力、潮湿应力、盐雾应力和油污应力等。损伤应力的作用效果通常表现为船用设备传感器内部元件性能退化或内部结构损伤，损伤应力对传感器的损伤是缓慢且细微的，只有损伤积累到一定程度时才引发故障。例如，电应力和稳态温度应力使内部元件逐渐老化。潮湿应力、盐雾应力和油污应力等会腐蚀内部元件，导致电系统的电性能参数不断发生退化，引起传感器输出信号的误差量逐渐增大，最终超过允许范围。温度循环应力使内部材料不断承受温度变化产生的热应力。机械振动应力不断给内部材料施加交变机械应力，导致传感器内部结构出现结构损伤，累积的结构损伤最终引起内部结构断裂。根据上述分析，损伤应力中，电应力、稳态温度应力、潮湿应力、盐雾应力和油污应力等是导致传感器软故障的主要原因，而温度循环应力和机械振动应力是导致传感器硬故障的重要原因之一。

综上所述，船用设备传感器的故障模式可分为硬故障和软故障。硬故障由过应力和损伤应力中的温度循环应力、机械振动应力导致，软故障由损伤应力中的电应力、稳态温度应力、潮湿应力、盐雾应力和油污应力导致。

1.2 船用设备传感器的可靠性模型

1）硬故障可靠性模型。船用设备传感器的硬故障可以分为突发型硬故障和渐发型硬故障。突发型硬故障主要由过应力导致，具有偶然性，其故障率较为恒定；渐发型硬故障主要由温度循环应力和机械振动应力的累计损伤效应导致，该过程较缓慢，故障率呈缓慢上升趋势。但在实际情况中，温度循环应力和机械振动应力会造成船用设备传感器内部结构的强度持续下降，从而使船用设备传感器可承受的过应力水平不断下降。因此，随着传感器使用时间的增加，实际上其突发型硬故障的故障率同样呈上升趋势，总体上传感器硬故障的故障率呈明显上升趋势。对于此类情况，可以考虑使用双参数Weibull 分布作为船用设备传感器硬故障的故障分布模型[3]。其概率密度函数fhf和分布函数Fhf分别为：

式中，t为传感器的使用时间；γ和η分别为Weibull分布函数的形状参数和尺度参数。

2）软故障可靠性模型。引起船用设备传感器软故障的载荷环境应力主要包括电应力、稳态温度应力、潮湿应力、盐雾应力和油污应力等，这些损伤应力会造成船用设备传感器内部元件的电性能参数随时间发生缓慢且细微的变化，使零位电压发生漂移，导致传感器的测量误差随时间逐渐增大。该变化过程是典型的性能退化过程，可以考虑使用Wiener 过程性能退化模型作为软故障的故障模型[4]。

船用设备传感器的性能退化具体表现为零位电压发生漂移，当零位电压漂移量超过允许的范围时，则发生性能退化故障[5]。因此，设零位电压为性能退化参数X(t)，可表示为：

式中，μ为漂移系数，表征零位电压的平均增加速率；σ为扩散系数，表征漂移过程的波动幅度；B(t)为标准布朗运动，B(t)～N( 0，t)，反映了漂移过程中的随机性。

根据线性Wiener过程，零位电压具有平稳独立增量，在Δt时间内的增量ΔX(t)服从正态分布，即ΔX(t)～N(μΔt，σ2Δt)。假设每次传感器调零校准后的零位电压初始值为0，故障阈值为D，当零位电压漂移至D时传感器发生软故障，以零位电压首次到达阈值D的时间T作为传感器的软故障发生时间：

根据定理，首次到达时间T服从逆高斯分布，其概率密度函数fsf和分布函数Fsf分别为：

式中，Φ为标准正态分布的分布函数。

3）基于竞争故障理论的船用设备传感器可靠性模型。竞争故障是指对于具有多种故障模式的产品，当产品发生任意一种故障时，其他故障将不再发生，产品的最终故障是多种故障模式相互竞争的结果。竞争故障模型主要取决于故障模式之间的相关性，对于各故障模式相互独立的情况，通常将产品作为串联系统进行可靠性建模[6]。

根据船用设备传感器的故障机理，导致船用设备传感器发生硬故障和软故障的应力种类有较大差异，2 种故障模式之间不存在明显的相关关系。因此，在假设硬故障和软故障相互独立的条件下，船用设备传感器的故障模型可以由硬故障和软故障的串联模型表示，故障分布函数F可以表示为：

式中，t1为传感器的总使用时间；t2为传感器调零校准后的使用时间。

2 船用设备传感器的可靠性模型参数估计方法

船用设备传感器的现场数据是可靠性模型参数估计的重要依据，主要指其在使用过程中所记录的故障时间数据，包括硬故障时间数据、软故障时间数据和删失时间数据。但在实际情况中，由于可靠性数据是船东和船厂的核心商业机密，致使可收集到的可靠性数据样本量较小。并且在预防性维修工作机制的影响下，为预防故障的发生，船用设备传感器通常在发生故障前被维修或更换，造成可靠性数据中充斥着大量删失数据。总体上，现场数据中包含的有效可靠性数据信息量不足，严重影响可靠性评估的精度。而且这些传感器通常价格昂贵，由于成本限制，无法通过可靠性加速试验补充可靠性数据。

基于上述情况，船用设备传感器可靠性模型的参数评估应重点关注故障次数占比较高的故障模式，扩充该故障模式的可靠性数据信息量以提升其可靠性评估精度，进而提升船用设备传感器的整体可靠性评估精度。根据实际经验，船用设备传感器的软故障发生频率较高，平均故障间隔时间较短，应予以重点关注，需要采集退化数据作为软故障数据的补充。

假设船用设备传感器的现场数据中，有m个硬故障时间数据，记为X=(x1，x2，…，xm)，有n个硬故障的删失时间数据，记为Y=(y1，y2，…，yn)；有k个软故障时间数据，记为A=(a1，a2，…，ak)，有r个软故障的删失时间数据，记为B=(b1，b2，…，br)。同时测得另外p个传感器的退化数据，记为U=(U1，U2，…，Up)；对于其中第i个传感器，在时刻Wi=(wi1，wi2，…，wiq)共测得q个零位电压数据，记为Ui=(ui1，ui2，…，uiq)。对于这种可靠性数据包含有较多删失数据的情况，通常采用极大似然法进行参数估计。

1）硬故障的可靠性模型参数估计。设硬故障分布函数的待估参数为θ1=( )γ，η，其对数似然函数可表示为：

式中，xi为记录的第i个硬故障时间数据；yi为记录的第i个硬故障删失时间数据。

2）软故障的可靠性模型参数估计。为了使可靠性数据得到充分利用，需要融合现场数据和退化数据进行软故障的可靠性模型参数估计。假设已知软故障的故障阈值D，记第i个传感器的第j个退化时间间隔为Δwij=wij-wi(j-1)，记Δuij=uij-ui(j-1)是该退化时间间隔内的零位电压增量。设软故障分布函数的待估参数为θ2=( )μ，σ，其对数似然函数可表示为：

式中，ai为记录的第i个软故障时间数据；bi为记录的第i个软故障删失时间数据。

显然，式（8）和式（9）极为复杂，无法直接写出待估参数θ1和θ2的极大似然方程解析表达式。对于这种情况，可以将θ1和θ2的求解问题看作式（8）和式（9）的最大值优化求解问题，常用的方法有牛顿迭代法、遗传算法、粒子群算法、模拟退火算法等。本文使用模拟退火算法求解，借助R软件的GenSA程序包实现。

3 实例计算

某压力传感器工作在典型的船舶机舱环境中，用于测量管路压力，其零位电压的故障阈值D为50 mV，固定维护周期为半年，即每182 天进行一次传感器调零校准。收集到30 个传感器在2 年内的现场数据，共有5个传感器发生硬故障，硬故障时间数据记为X=( 521，539，621，647，655 )，其余25 个传感器均未发生硬故障，硬故障删失时间数据记为Y=( 730，730，…，730 )。同时每半年对传感器进行校准，记录到6次软故障，软故障时间数 据记为A=( 1 64，165，169，170，173，176 )，另有114 个软故障删失时间数据，记为B=(182，182，…，182 )，以上时间数据单位均为“天”。又收集到另外10 个传感器使用90 天、每6天测量一次的零位电压数据，得到零位电压随时间的变化曲线如图1 所示，在测量期间这10 个传感器均未发生任何故障。

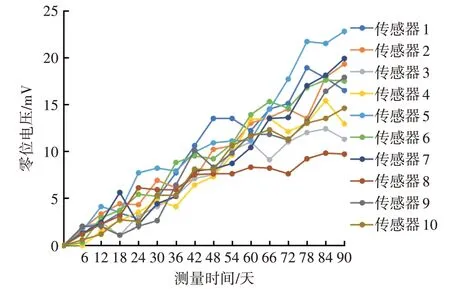
图1 零位电压随时间的变化曲线

根据式（8），借助R软件的GenSA程序包，求解硬故障分布函数的待估参数，算得γ= 5.144 4，η= 1 012.691 3，硬故障的累积概率曲线见图2。从图2 中可知，该传感器在使用2 年后硬故障的累积概率为0.169 4，使用3 年后累积概率为0.775 7。根据历史数据，该类型传感器在使用3 年后约有80%出现硬故障，与本文推测的概率较为吻合。

图2 硬故障的累积概率曲线

使用Shapiro-Wilk 法检验零位电压增量的正态性，得p值等于0.701 3、大于0.05，表明零位电压增量服从正态分布，可以认为传感器的退化过程符合线性Wiener 过程。根据式（9），借助R软件的GenSA 程序包，求解软故障分布函数的参数，算得μ= 0.428 9，σ= 0.607 4，软故障的累积概率曲线见图3。图3 中，虚线表示只使用现场数据进行参数估计的计算结果。由图3 可知，2 种参数估计方法计算出的曲线在初始阶段几乎重合，但从约180 天开始有明显差异。这是因为软故障的现场数据在第182 天出现删失，不包含182 天之后的软故障信息，而退化数据中包含了全周期的软故障信息，导致曲线的后半段存在明显差异。相比只使用现场数据的参数估计方法，融合退化数据和现场数据的参数估计方法使用了更多的可靠性数据，其估计精度更高，更符合实际情况。

图3 软故障的累积概率曲线

根据式（7），以该类型传感器使用360天、并在第360 天重新调零校准后的故障分布函数为例，其总故障的累积概率曲线如图4 所示。由图4 可知，总故障的累积概率曲线与软故障累积概率曲线的变化趋势保持一致，表明在该阶段软故障是该船用设备传感器的主要故障模式，提升软故障的估计精度可以有效提升船用设备传感器的整体可靠性评估精度。软故障的累积概率曲线在510天后快速上升，至660天时，软故障的累积概率已超过0.80，远大于硬故障的累积概率，表明该传感器的软故障平均故障间隔远小于硬故障平均故障间隔，软故障的期望发生次数更高。因此，在该传感器的使用过程中应重点关注软故障，制定相关预防措施，以减少传感器的故障发生率。

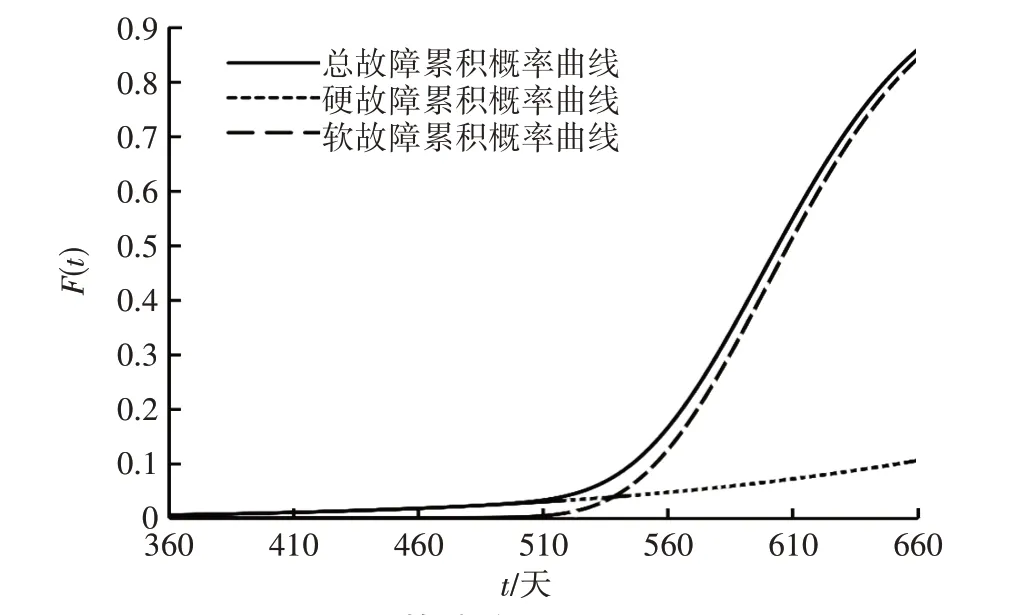
图4 总故障的累积概率曲线

4 结束语

本文建立了考虑硬故障和软故障的船用设备传感器可靠性模型，并给出了可靠性模型的参数估计方法，进一步提出了融合现场数据和退化数据的可靠性评估方法，解决了现场数据中缺少有效可靠性数据的问题，提升了船用设备传感器的可靠性评估精度。经实例应用表明，Weibull 分布和逆高斯分布可以分别较好地拟合船用设备传感器的硬故障和软故障，基于极大似然法和模拟退火算法的可靠性模型参数求解方法是可行的，且融合现场数据和退化数据的改进可靠性评估方法可有效改善软故障的数据删失问题。本文提出的可靠性评估方法可以为多种船用设备传感器的可靠性评估工作提供参考，对后续开展冗余设计、可靠性选型等可靠性工作具有一定的工程价值。