基于改进烟花算法的含风电场电力系统无功优化
2024-01-16胡书举李文彪霍文燕
犹 杰,胡书举,臧 琛,李文彪,霍文燕
(1.内蒙古工业大学能源与动力工程学院,内蒙古自治区 呼和浩特市 010051;2.中国科学院电工研究所,北京市 海淀区 100190)
0 引言
“十四五”是实现我国碳达峰的关键时期,大力发展风电产业既能落实双碳目标要求,也能为风电产业带来历史性的机遇[1-4]。近年来,风电相对其他新能源发电拥有更加良好的竞争力[5],但是大规模风电场接入电网,会给电力系统带来离散化、电压越限、电能损耗增大等无功问题[6]。通过无功优化可减少电力系统有功网损、改善节点电压分布[7-8]。这是提高电力系统电压质量的重要措施之一,同时也是保证电力系统安全、经济运行的一种有效手段。因此,为维持电力系统的稳定性和经济性,无功优化已成为当下研究热点之一。
为兼顾系统的经济性和稳定性,国内外学者已提出多种算法以应对含风电场的电力系统无功优化问题。文献[9]结合学习自动机法与模糊聚类理论的特点将多目标问题转化为单目标问题,但反映优化的结果不够准确。文献[10]为准确反映优化结果,建立了无功补偿装置收益最大、有功网损最小、电压偏差最小的多目标优化模型,但其采用的粒子群算法仍存在一定局限性。
智能优化算法的广泛使用,使优化问题的求解方向更具有多样性;但依然存在收敛速度慢、全局搜索能力低和易陷入局部收敛等问题。文献[11]通过改进遗传算法的交叉、变异对含风电场的电力系统无功配置优化问题进行求解。文献[12]结合自适应控制策略与粒子群算法对风电场并网进行无功优化求解。上述所提及方案虽然增强了算法自身的收敛性,但依然没有解决易陷入局部收敛、全局搜索能力低的问题。针对这一情况,文献[13]对分布式电源场景进行划分,采用烟花算法对配电网无功优化进行求解,利用烟花算法具有简单性、多样性、爆发性等特点,在保证收敛效率的同时提高了配电网无功优化的全局搜索能力。文献[14]为减少原始烟花算法的无效搜索,引入柯西变异代替高斯变异,提出一种自适应爆炸半径的精英烟花。该算法对含分布式能源的配电网进行无功优化,提高了寻优成功概率。虽然以上改进算法均在收敛性和全局性方面有所提升,但并未有效解决自身算法易陷入局部收敛及增强全局搜索能力的问题。
因此,本文针对含风电场的电力系统在求解无功优化时存在的局部易收敛、全局搜索能力差等问题,将含风电场的电力系统作为研究对象,建立有功网损最低、电压偏差最小的多目标无功优化模型。通过改进烟花算法的爆炸方式,提出一种多目标矢量烟花算法以求解无功模型的新方案。分析计算表明,该算法具有良好的收敛性和全局搜索能力。
1 风力发电机的数学模型
1.1 风力发电机的有功输出特性
风力发电机的功率输出会随风速变化而变化,如图1所示。图中:vi为切入风速;vr为额定风速;vo为切出风速;Pr为风力发电机的额定功率。

图1 风力发电机功率输出特性曲线Fig.1 Output characteristic curve of wind turbine power
由风力发电机功率输出曲线可得风力发电机输出功率Pw与风速v的表达式[15]如下:
式中:k1=Pr/(vr-vi);k2=-k1vi。
由式(1)可知,随着风速的变化可将风力发电机的输出功率分为3个阶段,分别为停机阶段、欠额定运行阶段和额定运行阶段。
1.2 双馈风电场的无功输出范围
双馈风力发电机的无功出力受其有功功率和机端电压的影响,由于机端电压恒定,风速大小通过影响有功出力而影响双馈风力发电机无功输出的范围。根据转子换流器容量的转子最大电流可获得单台风机无功输出范围[16]:
式中:X1、Xm分别为定子电抗和励磁电抗;U1为风电机组机端电压;IRmax为转子侧最大电流;Qw为单台风机无功输出。随着风速增大,有功输出范围逐渐扩大,无功调节范围逐渐缩小。
将上述双馈风力发电机的运行方式均采用恒功率运行,所以风电场以恒功率运行方式接入电力系统。为简化电力系统潮流计算模型,本文引入了风电场集总模型,忽略风电场内部各台风机之间出力的相互影响,将风电场中多台风力发电机等效成单台风力发电机模型。假设风电场内部的每台风机的工作参数一致,且在理想状态下运行,则其等效输出为
式中:PF、QF为等效风电场输出的有功和无功功率;Pm为风电场内部风机m输出的有功功率;Qmmin和Qmmax分别为风电场内部风机m无功调节最小值和最大值;n为风电场内部风机的总台数。
2 电力系统多目标优化模型
本文从电力系统运行的稳定性、安全性、经济性出发,建立以有功网损最低、电压偏差最小为目标的双目标优化模型。以PQ型风电场为例,本文建立了含风电场的电力系统无功优化模型。
建立的目标函数如下:
式中:Ploss为有功网损;dU为节点电压总偏移量;Gij为节点i、j之间的支路电导;Ui、Uj分别为节点i、j的电压幅值;δij为节点i、j之间的电压相角差;NL为系统节点集合;Uimax和Uimin分别为节点i的电压允许上限和下限。
为保证电力系统电能质量、运行安全性和经济性,所优化的变量需满足一定的约束条件,这些约束条件可分为等式约束和不等式约束。
(1) 等式约束。
根据系统功率平衡条件,采用系统节点的有功和无功功率平衡作为等式约束条件,即满足潮流约束平衡,其表达式如下:
(2) 不等式约束。
系统运行时,控制变量会机械受限,所以选择将发电机并网点电压变化量、变压器分接头变化范围及无功补偿容量和风电场无功出力范围作为不等式约束条件,如下:
3 多目标矢量烟花算法
3.1 基本烟花算法
烟花算法主要是由爆炸算子、变异算子和选择策略组成[17]。爆炸算子作为烟花算法重要组成部分,决定了烟花爆炸的强度和爆炸后产生火花的数量。对于第ζ个烟花xζ,其爆炸强度Aζ和爆炸后产生的火花数量Sζ定义如下:
为使烟花爆炸后产生的火花数量适量,对火花的数量做出如下限制:
式中:a和b为常数;函数round(x)表示对变量x进行四舍五入取整。
变异算子是烟花产生火花的重要步骤,主要由位移操作、变异操作、映射规则组成。位移操作是通过对一共c维的烟花从中随机选择z(z<c)个维度进行维度值的变化进而产生正常火花。
对第ζ个烟花的第L(1≤L≤z)维度上的值通过位置操作产生的正常火花xLψ(1≤ψ≤Sζ)定义如下:
式中rand(-1,1)表示区间(-1,1)内的随机数。
为增加产生火花的多样性,烟花算法引进了高斯函数,通过变异操作所产生的高斯变异火花定义如下:
式中函数randGauss(1,1 )表示满足均值为1、方差为1的高斯分布的随机数。
在产生火花的过程中,位移操作和高斯变异操作可能会使产生的火花落在搜索空间之外。因此,需将超出搜索空间的火花映射回搜索空间内,其映射规则定义如下:
式中:xLmin和xLmax分别为超出边界的第ψ个正常火花的第L维的下边界值和上边界值;和分别为超出边界的第ψ个变异火花的第L维的下边界值和上边界值;⊗为取模运算,A⊗B=A-,其中floor(x)表示向下取整。
对于烟花的选择策略,在当代烟花和烟花每个步骤生成的火花中,选择一定数量较好的个体,将其作为下一代烟花,对种群进行更新。
3.2 改进的多目标烟花算法
多目标问题的最优解并非单一,因此需要找寻一组折中解,该折中解的集合则为帕勒托解集[18]。为增强烟花算法求解多目标问题的能力,主要从2个方面改进烟花算法:(1)对烟花算法的搜索资源进行精细化分配,在平衡全局搜索和局部搜索的基础上,将同一烟花的不同维度进行关联,进一步挖掘算法的搜索能力;(2)在选择策略上引入新型的拥挤度计算方式来替代传统的拥挤度计算,从而获得更高质量的帕勒托解集。
对于同一迭代中的烟花种群爆炸的半径设置,根据个体烟花之间的帕勒托支配强度差异进行分配适应度值,其计算公式为
式中:ft(xζ)为第t代种群NPt中烟花个体xζ的适应度值;xζ≺xφ表示烟花个体xζ对另一个烟花个体xφ的帕勒托支配;〈·〉表示烟花个体xζ支配了种群中其他烟花个体的数目。
第t代种群NPt的最大适应度值ftmax定义为
第t代种群NPt的爆炸半径采用非线性递减的半径变化方式,以保持全局搜索和局部搜索的平衡。其爆炸半径r(t)定义为
式中:τ为常数;Dcmin和Dcmax分别为当前种群中所有烟花各决策维度的最小值和最大值;Tmax为最大迭代次数;α为爆炸衰减常数;rend为预设的最小爆炸半径。
根据式(13)—(15)可知个体烟花xζ∈NPt的爆炸半径rζ(t)为
因此,对于烟花xζ产生火花的方式也随之改变,为
式中:rζh=,为烟花在h层爆炸的半径,h=1,2,…,ω;β为烟花的第β维度,1≤β≤c。
式(17)所示火花产生方式主要是烟花随维度进行爆炸而产生火花,没考虑到维度之间的影响。为进一步挖掘算法的搜索能力,通过改进一种新型变异方式来增加火花的多样性,其变异火花产生的方式为
式中γ为烟花的随机多个维度,其不大于烟花决策总维度。
由于烟花产生的火花数量较多,为获取更高质量的帕勒托解集,借鉴文献[19]所提出的拥挤度计算方式代替传统拥挤度计算。新型拥挤度距离计算方式定义如下:
式中:μ为优化目标函数的个数;eD为点e的拥挤度;fg,e+1和fg,e-1分别为离点e最近的2个点的第g个目标的函数值;ed=,为传统拥挤度距离。
3.3 多目标矢量烟花算法流程
将改进后的多目标烟花算法(multi-objective fireworks algorithm,MOFWA),即多目标矢量烟花算法(multi-objective vector fireworks algorithm,MOVFWA)应用到无功优化中,可满足无功优化中多目标函数的要求。因此,在Matlab软件中编写多目标矢量烟花算法程序,并设定算法种群规模NP=100,最大迭代次数Tmax=100,爆炸衰减常数α=0.3,预设的最小爆炸半径rend=0.00001。无功优化的算法流程如图2所示。

图2 无功优化算法流程图Fig.2 Algorithm flow chart of reactive power optimisation
本文所含风电场电力系统多目标无功优化模型的具体求解步骤如下:
(1) 初始化参数。设置多目标矢量烟花算法最大迭代数Tmax、爆炸衰减指数α、最小爆炸半径rend、种群数量NP等参数;根据发电机并网点电压变化量、变压器分接头变化范围及无功补偿容量和风电场无功出力范围的约束条件,随机初始化种群。
(2) 评估烟花爆炸半径。采用牛顿拉夫逊潮流计算得出当前烟花种群的适应度值,结合式(13)—(16)计算所有个体烟花的爆炸半径。
(3) 爆炸产生火花。所有烟花根据式(17)(18)爆炸获得火花。
(4) 更新种群。按式(19)计算所有火花的拥挤距离,并根据自适应精英保留策略选择种群中的精英个体,将其作为下一代烟花。
(5) 检查是否满足迭代条件。若满足,则输出帕累托前沿曲线及曲线中每个个体对应的优化控制策略;如不满足,则迭代次数+1,返回步骤(2)。
本文提出的改进多目标烟花算法的优化流程如图3所示。
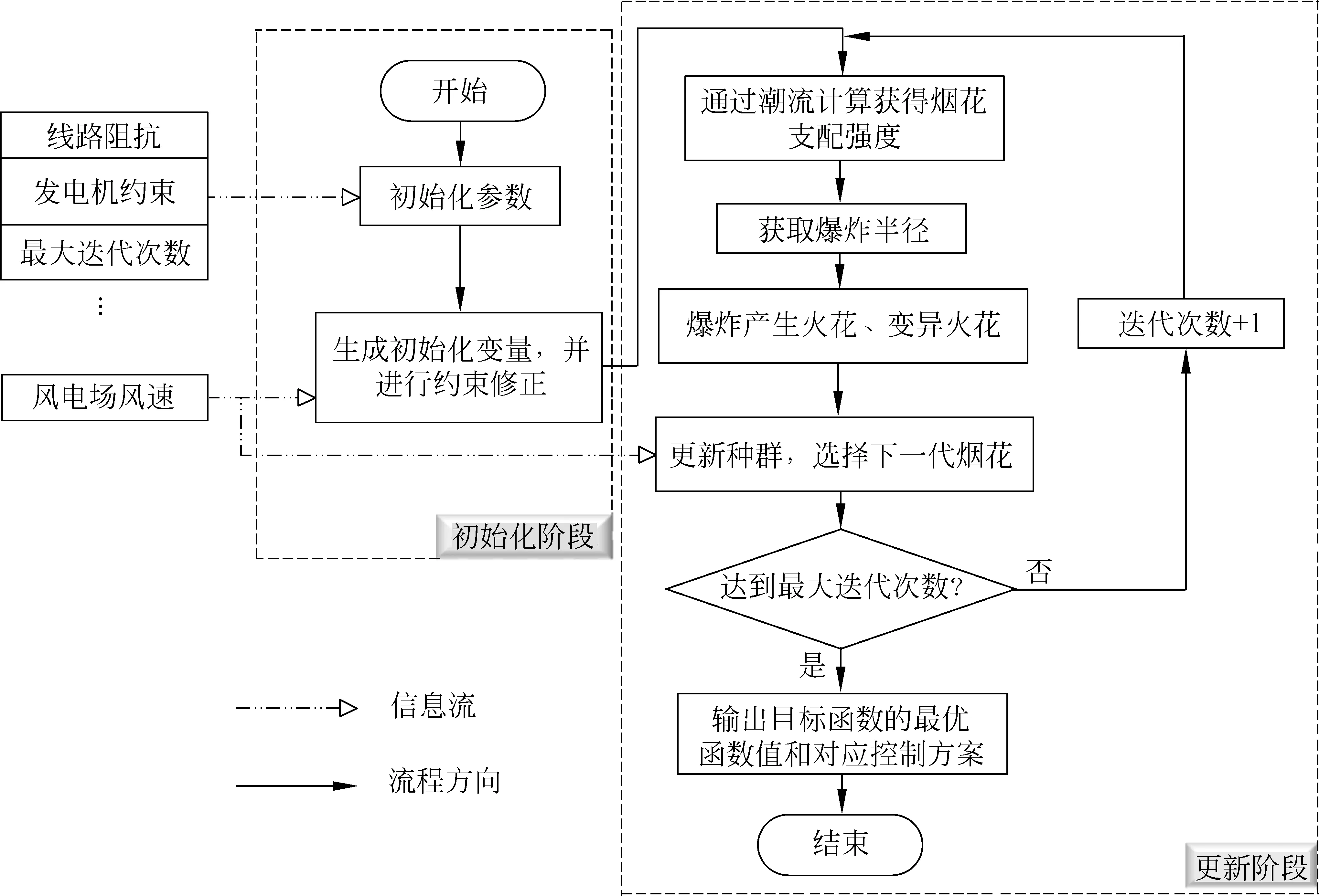
图3 本文多目标烟花算法的优化流程Fig.3 Optimization process of the multi-objective fireworks algorithm in this paper
4 算例分析
本文以图4所示IEEE 14节点系统为算例,对算法进行验证。IEEE 14节点系统三相功率的基准值为100MV·A,线电压的基准值为23kV,优化结果均采用标么值表示。假设将风电场作为电源接入节点9,该风电场由40台额定容量为1.5MW的双馈风力发电机组成,切入、切出和额定风速分别为 3.5、25和12m/s。

图4 IEEE 14节点电力系统Fig.4 IEEE 14-node power system
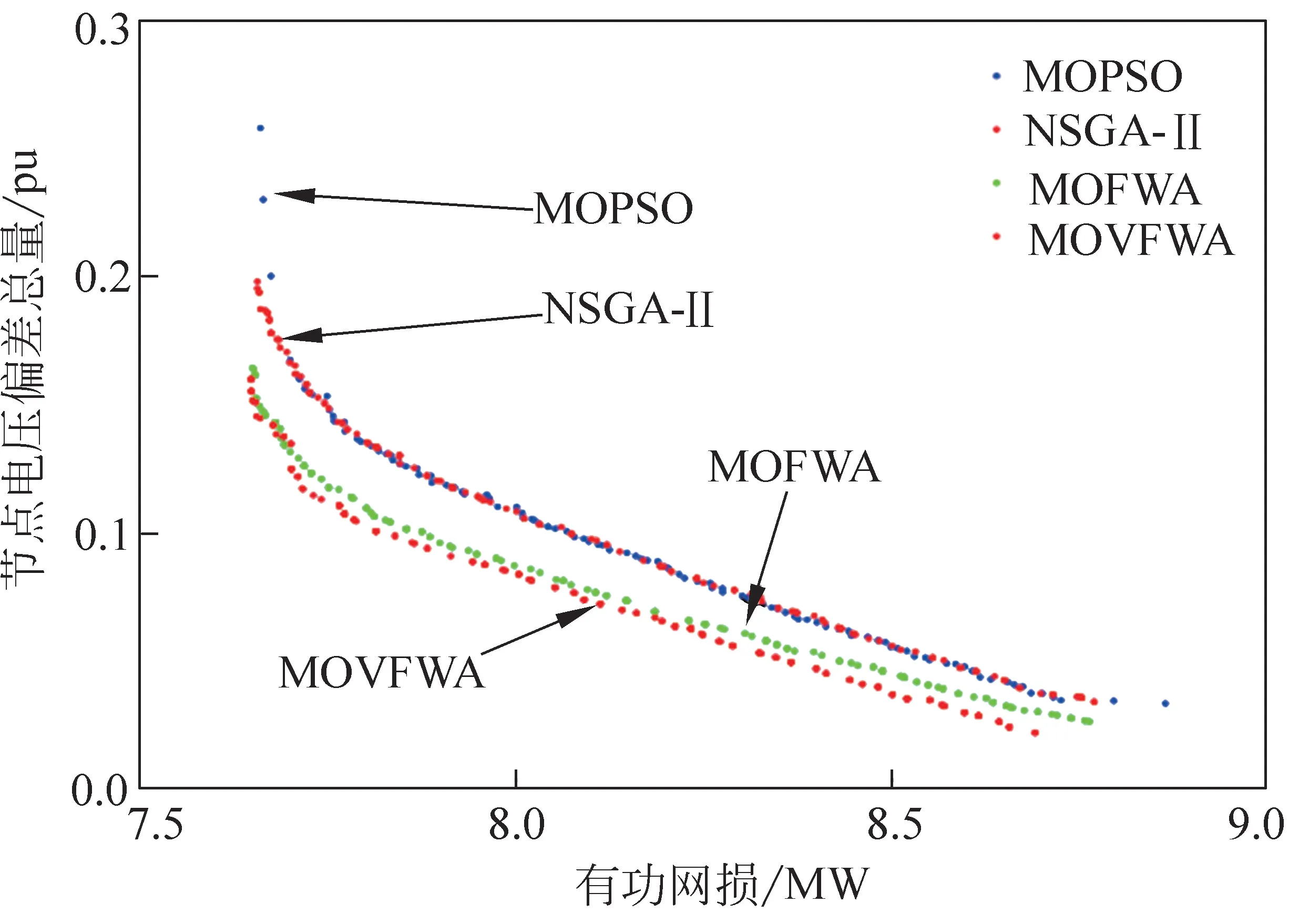
图5 无功优化模型的帕勒托解集Fig.5 Pareto solution sets for reactive power optimization models
4.1 算法优化性能分析
设置接入系统的风电场风速为20m/s,采用不同算法对比求解多目标无功优化问题,得到的帕勒托最优前沿如图 5所示。对比非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)、多目标粒子群算法(multi-objective particle swarm optimization,MOPSO)及MOFWA算法,改进后的MOVFWA 算法,其电压偏差量都保持在1.5pu以内,网络损耗也保持一定优势,优化得到的帕勒托前沿具有良好的全局性、寻优性和均匀性。
由于最优解集的数量较大,本文只列举部分最优解。各算法选1组最合适的帕勒托最优解集参数,将优化前与各算法优化后的方案进行对比,其优化方案的变化如表1所示。各算法优化后的目标结果与未优化前的目标结果对比如表2所示。
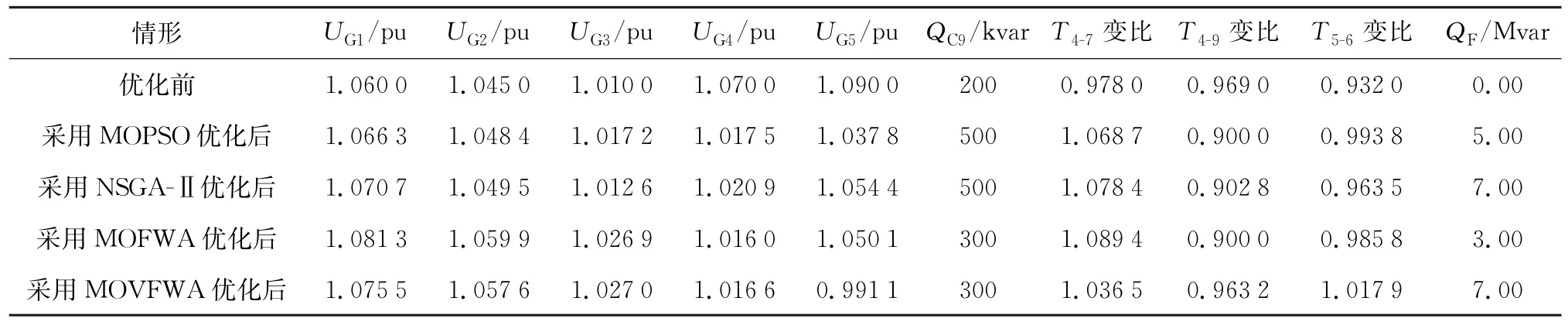
表1 无功优化前后方案对比Table 1 Comparison of solutions before and after reactive power optimisation
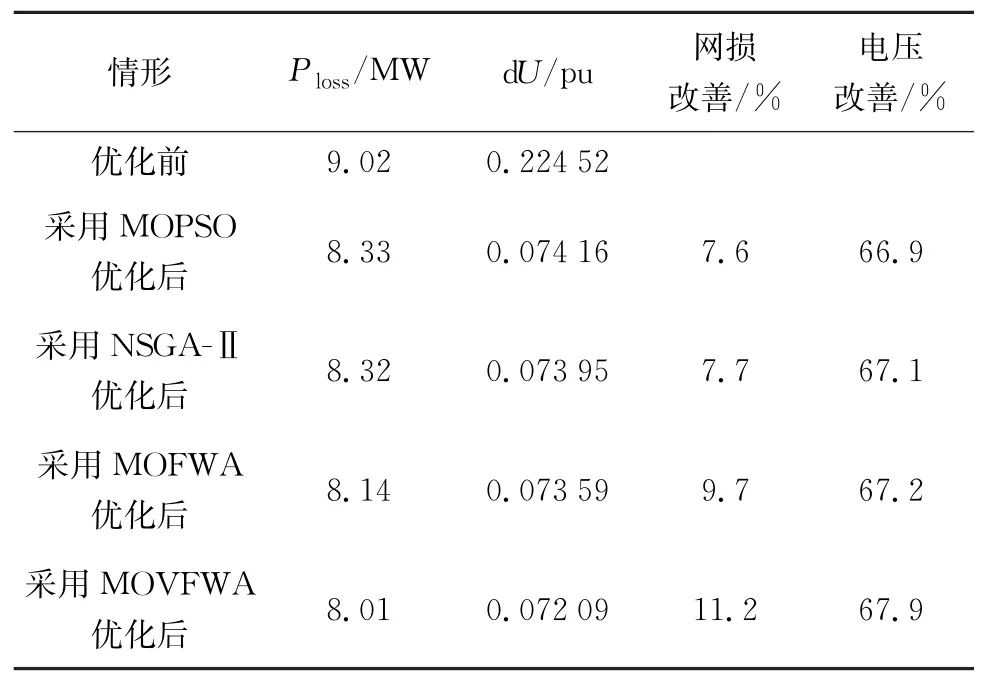
表2 含风电场的电力系统无功优化前后结果对比Table 2 Comparison of results before and after reactive power optimization of power system containing wind farms
由表1、2可见:采用各算法优化后,系统有功网损和电压平衡均有明显的改善,且本文所提出的MOVFWA算法改善效果明显优于其他算法;有功网损MOVFWA算法比未优化之前提升了11.2%,电压偏移量总体降低了67.9%。可见,相比其他算法,MOVFWA兼顾了局部与全局搜索能力,总体性能有所提升。
5 结论
本文提出的MOVFWA 算法通过改变烟花爆炸方式并关联烟花爆炸维度之间的影响,在增强烟花算法全局搜索能力的同时,避免了算法陷入局部最优解。该算法通过引入新型拥挤度计算,加快了算法的收敛速度。接入风电场的IEEE 14节点电力系统算例优化结果显示,相比其他经典算法,MOVFWA算法具有更高的无功优化性能。
