基于ADMM-GBS 的考虑风光不确定性的智能电网实时电价策略
2024-01-16张瑶嘉
张瑶嘉,高 岩
(上海理工大学管理学院,上海市 杨浦区 200093)
0 引言
随着国民经济和智能电网的快速发展,传统的能源利用模式已无法满足人们日益增长的能源需求。新能源发电的迅速发展给电力系统带来了不确定性和挑战,通过智能电网中的需求侧管理,可促进新能源发电的利用,实现削峰填谷目标,使供电侧和需求侧达到均衡,以此达到能源利用的最大化并提高社会经济效益。智能电网中,需求侧管理是最重要的因素之一,需求侧管理可对能源消费行为进行影响和优化,通过采取有效措施鼓励电力用户积极参与电力运行、优化用电方式,从而提高终端用电效率,保障电力供需平衡,实现供电成本最小化[1-6]。
基于需求响应的实时电价是智能电网环境下最理想的一种定价机制,实时电价根据实际的电力供需情况,连续反映电力边际值,具有兼顾电力供应商侧和用户侧利益的优势[7-9]。
在实时电价问题的解决过程中,目前主要采用2种办法,一种是从电力市场化的角度考虑,采用市场电价机制,主要利用博弈论方法[10-15]均衡供电侧和需求侧之间的关系,制定电价机制,利用博弈论方法可准确反映供电侧和需求侧的相互作用。文献[11]利用非合作博弈描述实时电价问题,得出用户最佳能源消耗;文献[12]针对具有发电设备和储能设备的用户提出了供电方利润最大化的双层规划实时电价方案,在市场定价方面,不同发电商会考虑自身利益,相互之间形成竞争关系,构成Stackelberg博弈[13];文献[14]在Stackelberg博弈模型的基础上引入可时移负荷,设计供电方与用户之间的主从博弈模型,以确定最优交易电价;文献[15]在引入负载预测基础上,设计与之适应的电力价格差价模型和失衡成本模型,建立了供应商与电力用户之间的博弈模型。
另一种方法是从公共产品角度考虑,采用社会福利最大化的电价机制[16-22],在智能电网实时电价策略研究中,社会福利最大化模型同时兼顾了供需双方的利益。文献[16]提出了社会福利最大化模型,实现了用户侧的效用最大化和供电方的成本最小化;并以供电与用电的平衡为约束条件,采用对偶方法制定了分布式对偶次梯度算法,该算法模拟了用户与能源供应商之间的动态过程,但该算法在优化过程中存在收敛速度较慢的问题。针对算法在优化过程中存在的问题,文献[21]将社会福利最大化模型转换为非光滑方程,提出了一种新的平滑共轭梯度方法来解决基于社会福利最大化的智能电网实时电价问题,保证了算法的收敛性与收敛速度。此外,许多文献采用交替方向乘子法(alternating direction method of multiplier,ADMM)[23-25],该算法是一种具有分布式计算能力,解决可分离凸优化问题的有效方法;可将大规模问题分解为若干较小问题,再通过协调子问题的求解,得到整体问题的解;综合了乘子法良好的收敛性和对偶上升法的可分解性,分布式算法相较于集中式算法具有更高的经济性、灵活性和扩展性[23]。文献[23]提出了一种面向电网系统的ADMM 算法,建立了双层优化模型,利用模型变量间的可分离性保证了算法的分布式求解。文献[24]考虑了基于日前实时电价的需求响应,结合虚拟代理提出了改进ADMM 算法,更好地保证了用户的隐私性。ADMM 算法是求解2个可分离变量的凸优化问题的有效工具,针对3个算子的问题,直接推广形式不能保证算法的收敛性。文献[26]提出了高斯回代的交替方向乘子法(ADMM with Gaussian back substitution,ADMM-GBS),将ADMM 算法推广到多个变量的凸优化问题,并应用于实时电价策略中。
除了对算法进行改进,许多学者还从不同角度对电力模型进行了改进,比如考虑到用户侧的电器分类[18-19],考虑电力来源的多样性和不同电力来源的变化特征,使用光伏和化石燃料2种类型的能源互补供电[20-21]。受各种因素影响,新能源电力具有反调峰性、随机性、波动性等特点,使可再生能源发电利用率不足、“弃光弃风”等问题突出。文献[27-28]考虑了风光不确定性在智能电网中的影响,根据历史风速和光照数据建立风光联合出力的电力模型。在“双碳”目标下,如何建设更加经济、环保和低碳的电力系统已成为全国电力行业的共同课题。市场机制作为解决二氧化碳为代表的温室气体减排问题的新路径,把二氧化碳排放权作为一种商品,形成了二氧化碳排放权的交易,碳市场中对发电产生碳约束,使火力发电成本增加,推动了发电的清洁化和高效化。所以,在电力市场中考虑碳交易机制[27],对促进新能源发展、建设环境友好型社会有重要意义。
文中结合目前的智能电网实时电价策略,考虑发电公司与用户双方的利益,设计一个考虑碳交易机制与风光不确定性的电力系统。该模型充分考虑可再生能源在电力系统中的重要性及风力发电的随机性,鼓励用户侧和发电公司生产新能源电力,模型以用户总效用最大、供电成本最小为目标,实现社会福利最大化。最后,运用针对3个子问题的分布式算法,即基于ADMM-GBS的分布式优化算法,验证了模型的合理性和有效性。
1 系统模型
考虑电力系统中有供电方和用户侧,其中供电方有2类,为火力发电和风力光伏发电。将1个用电周期划分为k个时段,K为一个周期所分割时段的集合,即k∈K={1,2,…,kmax},用N={1,2,…,imax}表示用户i的集合。
1.1 用户可再生能源发电
用户配备可再生能源发电设备,可自行生产可再生能源,其不具备存储功能,用户侧生产的可再生能源不并入电网,即各用户可再生能源发电量相互独立。假设:该设备发电成本与维护费用忽略不计;1个周期的发电量不足以覆盖用户1天所需电量;用户优先使用可再生能源发电电量。φi,k为用户i在时段k的出力,其服从正态分布N(μ,σ2),μ和σ2为设备实际参数,且均为正数。
1.2 碳排放交易机制
各碳源根据分配的配额有计划地制定或调节日前的调度生产计划,倘若在周期内实际产生的碳排放量比分配的配额多,则需要在碳交易市场上以当前碳交易价格购买超额配额;若实际碳排放量比配额少,则进入市场将多余的配额出售以获取收益。我国的碳交易政策中对碳源的分配主要采用无偿分配的方式,无偿的碳排放碳源主要来自于火力发电机,火力发电机在k时段内的无偿碳排放配额为
式中:Pk,T为火力发电机组在k时刻的输出功率;ε为单位电量的排放额度,由电量边际排放系数与容量边际排放系数加权平均而得。火力发电机实际的碳排放量为
式中αT、βT、γT为碳排放系数。
在实时电价背景下,碳交易将会增加供电侧成本,包括碳成本、技术成本和管理成本等,碳交易成本可表示为
式中δ为碳交易成本系数。
以碳交易价格为基准,建立一种基于碳交易激励机制的需求响应,供电方在出让电能消费权的同时,可将相应的碳排放权出售而获得收益。碳排放权收益表示为
式中:η为可再生能源的占比;q为新能源发电时的额外补贴奖励系数。
考虑碳排放权的碳交易成本为
1.3 风光不确定建模
确定性模型将风电预测值直接用于能量管理模型中,为一种不考虑新能源出力不确定性的模型。为更准确地描述新能源发电情况,采用风光不确定性模型。用M={1,2,…,mmax}表示风力发电机m的集合,用S={1,2,…,smax}表示火力发电机s的集合。风力发电的随机性依赖于风速变化的随机性,风力发电机发电机的出力模型[24]表示为
式中:vci、vco、vr、vk分别为风力发电机的切入、切出速度、额定风速、k时刻的风速;PP为风电额定输出功率;Pk,WT为k时刻风电输出功率。
风速服从Weibull分布,概率分布[27]表示为
式中ks和c分别为Weibull分布的形状参数和尺度参数,尺度参数能表示统计区间内风电场的平均风速大小。
光伏与太阳光照辐射有关,光伏发电机的出力模型为
式中:GR和G(k)分别为额定光照辐射和k时刻光照辐射;TR和T(k)分别为额定温度和k时刻温度;PPVR为光伏额定输出功率;Pk,PV为k时刻光伏输出功率;τ为实际光照强度。
基于上述风速与风电输出功率之间的关系以及风速所服从的概率分布,得到风电出力的概率分布:
式中h=-1,为中间变量。
新能源发电包含风力发电和火力发电,新能源供电在k时刻的总输出功率Pk,R定义为
1.4 发电成本函数
火力发电成本函数为严格的凸函数,采用二次函数作为成本函数,考虑碳交易成本的火力发电成本函数表示为
式中aT、bT、cT为火电机组的燃烧系数,aT>0,bT、cT≥0。
火力发电机出力约束表示为
全部用户与供电能力达到供需平衡,表示为
式中P(xi,k)为用户i在k时刻的用电负荷。
发电量超过负荷需求时会出现“弃风弃光”情况,风光电力的随机性会对实际用电产生欠估计和过估计。考虑新能源发电的不确定性带来的过估计和欠估计的惩罚成本,新能源发电的成本为
式中:等式右侧第1项为风力发电的直接成本,mWT为其成本系数;第2项为光伏发电直接成本,nPV为其成本系数;E(·)为期望函数,及分别为风力发电过估计期望值和欠估计期望值;第3项为风力发电欠估计惩罚成本,即对调度风力电能小于实际使用风力发电的惩罚,为其成本系数;第4项为风力发电厂过估计惩罚成本,即对实际使用风力电能小于调度风力电能的惩罚,为其成本系数。
1.5 效用函数
使用效用函数反应用电过程中随用电量变化的用户满意程度。文中使用的效用函数具有以下特点:(1)是非减函数;(2)边际效益非递减,即凹函数,用户的满意度水平能逐渐达到饱和。用户的效用函数为
式中:x为用电量;α∈(0,1),为预先确定的参数,根据每个用户用电情况提前设置;ω>0,为反应用户效用情况的参数,参数因用户而异。用户i在k时刻的效用函数可表示为Ui,k(xi,k,ωi,k)。
1.6 实时电价模型
用户侧福利等于用户效用减去支付的购电成本的期望,则用户侧福利函数表示为
式中yk为用户在k时刻购买电力的价格。
供电方福利为售电收入减去成本的期望,成本包含火力发电成本和新能源发电成本,供电方福利函数表示为
社会福利最大化是实现效用的最大值,即求得收益-成本比率的最大值。考虑用户侧和供电侧双方利益,社会福利最大化模型的目标函数是用户侧福利和供电方收益的总和最大,约束为总用电量不超过供电能力和发电机出力约束,则社会福利最大化模型为
式中λk为实时电价。
式(12)可视为辅助约束,在电力市场的消费过程中,可将优化问题分解在每一时段k∈K独立求解。在k∈K时刻固定时,社会福利最大化问题可转化为只需考虑某一时段的社会福利最大化问题,并将风力发电机、光伏发电机、火力发电机求和符号简写。考虑社会福利最大化目标的智能电网实时电价模型为
为方便后续计算分析,给出新能源发电成本C(Pk,R)的凸性分析。式(14)中风力发电过估计期望值和欠估计期望值分别定义为
式中:vj=vci+,是中间变量;Γ(·,·)为不完全Gamma函数。
计算其二阶导数为
由此可知风电成本函数为强凸函数,优化问题(20)为凸优化问题。
2 算法求解
2.1 ADMM-GBS 算法原理
ADMM 算法是一种用于求解具有可分解结构的凸优化问题的重要方法,ADMM 算法一般用于等式约束的凸优化问题,具体如下:
其中:f(xd)和g(yd)为目标函数分解成的2个子问题,xd、yd分别为f(xd)和g(yd)的自变量;xs和ys为f(xd)和g(yd)的共享变量;Αs、Bs和bs为共享变量耦合关系系数矩阵。然而,根据两算子的标准ADMM 算法得到的ADMM 三算子算法的直接推广形式不能保证算法的收敛性。因此,本文采用了ADMM-GBS算法对系统进行优化求解,该算法在3个算子直接推广形式的基础上增加了变量的校正环节,保证了算法的收敛性。3个算子的目标函数及拉格朗日函数分别为
式中:x、y、z为可分离算子;A、B、C为可分离算子参数;λ为乘子变量;ρ为惩罚因子,为常数。
ADMM 算法的直接推广形式表示为
式中:上标(k)、(k+1)分别表示第k及k+1次迭代后的值;argmin(·)为取得最小值时自变量的值。
直接推广的式(28)不能保证收敛,处理有关核心变量y、z子问题不对等。采取ADMM-GBS方法将(y(k+1),z(k+1),λ(k+1))当成预测点,ADMMGBS方法已被证明是收敛的,其校正公式为
式中:v为校正因子;I为校正参数。
2.2 模型求解
问题(20)的增广拉格朗日函数定义为
对于每个时刻k,先选择一个子问题P(xi,k)进行计算,待计算完成后暂停计算;并将共享变量的信息传递给另一个子问题,待子问题计算完成后暂停计算,并将共享变量的信息传回P(xi,k);每完成一轮计算后更新乘子变量λk。迭代计算过程可表示为
式中:xr、yr、zr分别为迭代中各子系统局部变量的最大偏差绝对值;ξ为收敛精度。
ADMM-GBS算法步骤为:(1)设置参数0<ρ≤1,ξ>0;(2)输入P(xi,k)、Pk,T、Pk,R初值和拉格朗日对偶变量λk∈(0,1);(3)式(32)子优化问题进行交替计算;(4)根据式(33)校正;(5)收敛判断,若满足终止条件式(34)算法终止,否则,令k=k+1,返回步骤(3)。
3 仿真模拟
3.1 参数设置
将1天分为24个时段,即每个时段1h。选取100个用户,供电方包含2个火力发电站、4个风力发电站和4个光伏发电站,智能电表可收集用户的用电信息进行统一调度从而有效保护用户的隐私。通过数值仿真来验证所提出的实时电价方案的有效性和可行性,设置火力发电Pk,T∈[50,320]kW;式(6)中vci=3km/h,vr=13km/h,vco=25km/h;式(11)中aT=0.01,bT=0,cT=0;校正因子v∈(0.90,0.95)。通过Matlab R2018a进行仿真分析。
3.2 结果分析
图1为负荷情况和负荷需求曲线,同时展示了风力光伏发电机、火力发电机、用户侧光伏发电情况。由图1可知:在08:00—17:00新能源发电较多,用户端在06:00—18:00参与发电,01:00—06:00属于用户的用电低谷期,07:00—19:00属于用户的用电高峰期,20:00—24:00属于用户的用电低谷期和高峰期之间。可见,总发电量可满足总负荷需求,两者之间的趋势基本相同,没有造成电力过多的浪费。
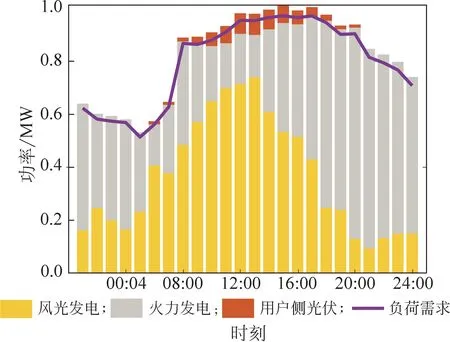
图1 负荷情况和负荷需求曲线Fig.1 Load situation and load demand curve
图2为全天的实时电价与分时电价,可见:实时电价与负荷需求曲线趋势相符。在负荷高峰期,电价随之上升;当负荷处于低谷期,电价下降。图3为1天的社会福利对比,可见:在02:00—15:00实时电价社会福利较大;16:00—01:00实时电价社会福利较低,实时电价福利总体高于分时电价福利;07:00—12:00实时电价福利远高于分时电价福利,采用实时电价可产生更多的社会福利。
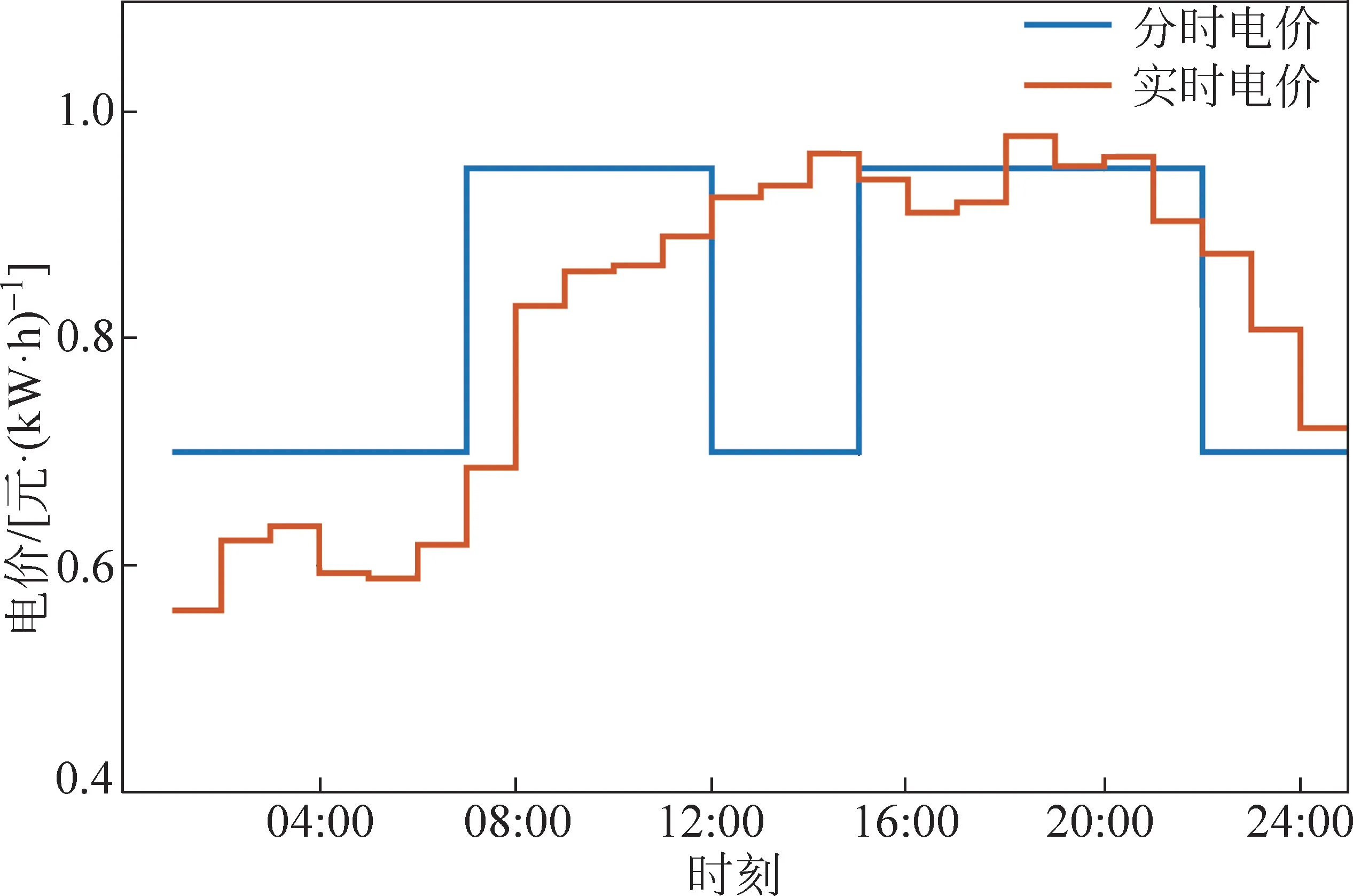
图2 24h的实时电价与分时电价Fig.2 24-hour real-time tariffs and time-of-day tariffs
图4所示局部变量间最大偏差绝对值验证了算法可收敛到全局最优解,当迭代达到次数为20次时,目标函数已经收敛,直到迭代达到48次时,偏差达到收敛标准。文中采用的ADMM-GBS算法可在一定的误差要求和有限的迭代次数内收敛到全局最优解。
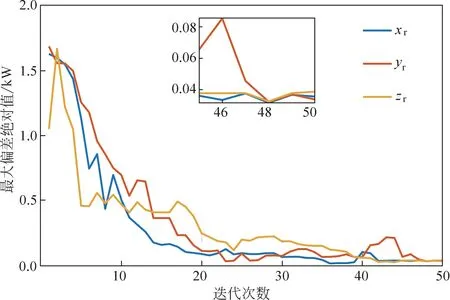
图4 局部变量间最大偏差绝对值Fig.4 Maximum absolute values of deviations between local variables
图5显示了考虑碳交易与不考虑碳交易对风光消纳的功率的影响,可见:当考虑碳交易时,可实现对新能源的完全消纳;当不考虑碳交易时,新能源消纳的功率较低,产生弃光弃风现象,降低了电网系统的运行品质。
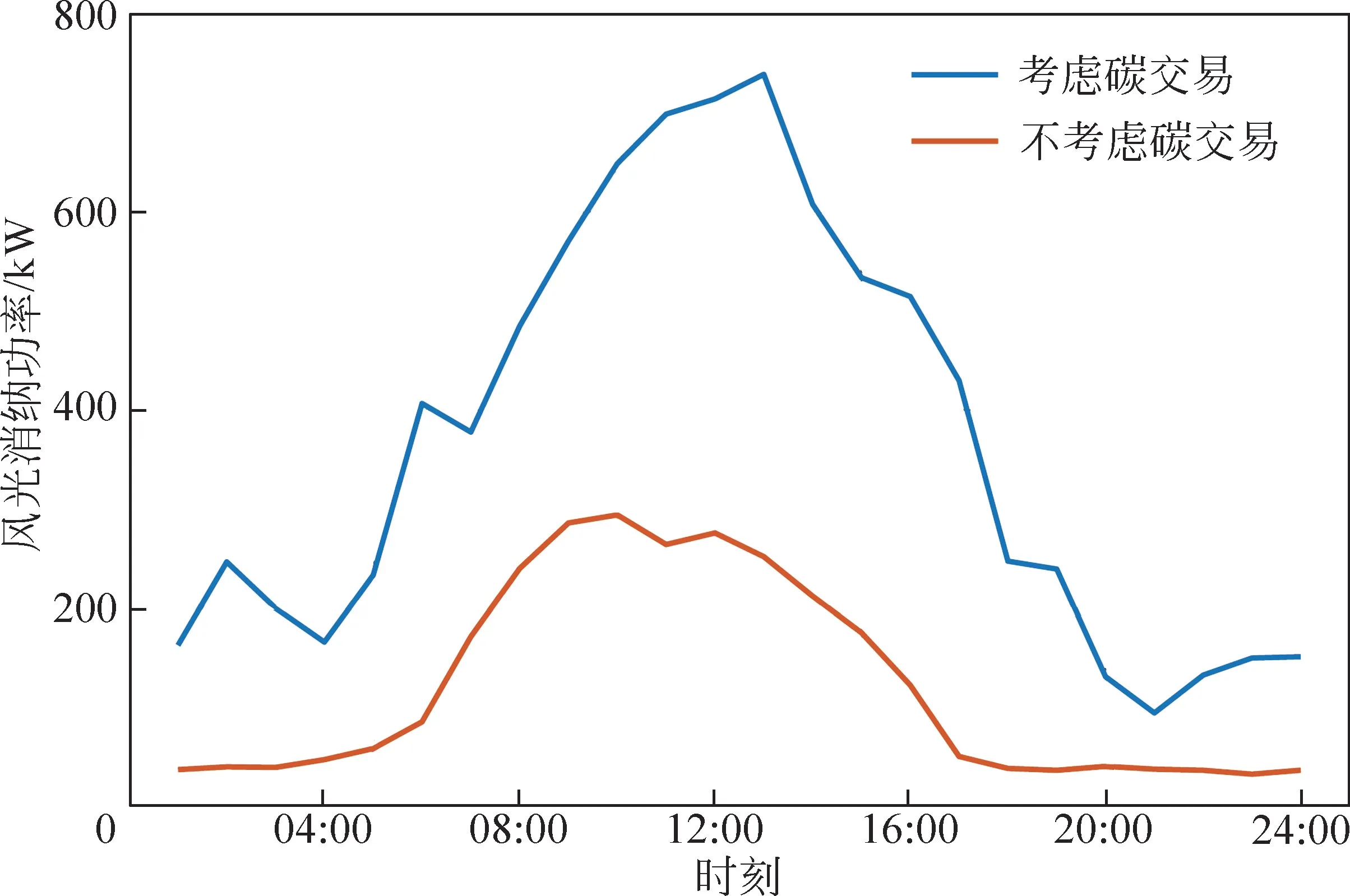
图5 碳交易对消纳功率的影响对比Fig.5 Impact comparison of carbon trading on consumption power
4 结论
智能电网中的实时电价是节约用电、削峰填谷的有效措施。本文考虑了碳交易机制、风光不确定性,在用户侧配备发电设备,以社会福利最大化为目标,设计出一种实时电价模型;并用ADMM-GBS算法求解该模型,仿真模拟所得的数据证实了模型的可行性。由此得到以下结论:
(1) 社会福利最大化模型可有效保证电力系统的供需平衡及用户和供电侧的利益,实时电价相较于分时电价可产生更高的社会福利。
(2) ADMM-GBS算法可在一定误差要求和有限的迭代次数内收敛到系统全局最优解,有效解决了不同子问题之间信息等各方面的障碍。
