Vibration Reduction and Torque Improvement of Integral-slot SPM Machines Using PM Harmonic Injection*

,,,

(School of Electrical and Information Engineering,Jiangsu University,Zhenjiang 212013,China)

Abstract: This study aimed to improve the vibration and torque of an integral-slot surface-mounted permanent magnet (SPM)machine by optimizing the shape of the harmonically injected permanent magnet (PM).First,the effect of the third harmonic injected into the sinusoidal PM shape on the electromagnetic performance of a 36-slot/12-pole SPM machine was investigated,including the torque performance and vibration response.It was found that the Sin+3rd harmonic-shaped PM had a contrary effect on the torque and vibration performance of the integral-slot machine,which improved the torque capability but worsened the vibration performance.Second,the response surface model and Barebones multi-objective particle swarm optimization algorithm based on a trade-off between the average torque and vibration were implemented to determine the optimal harmonic injection.Subsequently,the performances of the optimal Sin+3rd-shaped and eccentric PM machines were compared,showing the excellent torque and vibration performance of the adopted method.Finally,a prototype was manufactured and tested to verify the results of the theoretical analysis.

Keywords: Integral-slot,surface-mounted permanent magnet machine,multi-objective optimization,third harmonic,torque,vibration

1 Introduction

Owing to their high efficiency and power density,integral-slot surface-mounted permanent magnet (SPM)machines have been widely applied in areas such as servo drives and electricity propulsion[1-3].High torque performance and low vibration are required for integral-slot SPM machines to meet the growing need for high performance[4-6].However,a mutual restriction exists between high torque density and low vibration[7-9].Therefore,it is important to investigate an integral-slot SPM machine with a high torque performance and low vibration response.

Traditionally,eccentric permanent magnets (PM)have been identified as an attractive approach for reducing the torque ripple and electromagnetic vibration in machines.An eccentric PM was designed to reduce torque ripple[10-11],and the torque ripple and vibration performance were simultaneously improved[12].Low-and medium-frequency vibrations were reduced using eccentric PMs and dummy slots[13].However,most of the above studies were based on torque ripple and vibration reduction,resulting in an unacceptable drop in torque capability.

Numerous approaches have been proposed to improve the torque performance,among which PM shaping with harmonic injection is an effective method.Theoretical derivation and finite element analysis(FEA) indicate that an appropriate value of the third harmonic injected into the PM shape can increase the average torque while maintaining a low torque ripple[14-15].However,the optimal value of injected harmonics is unknown.A PM shape based on a feedback function was proposed to obtain a superior harmonic-injected amplitude,further improving the torque capability[16].In addition,the differences between various harmonic injection methods were explored,confirming the advantages of high-torque performance[17].The harmonic amplitude injected into a PM was adjusted using multi-objective optimization to obtain a higher average torque[18].The above studies indicate that a third-harmonic injected PM could enhance torque capability.However,the electromagnetic vibration performance was neglected.

For integral-slot machines,zeroth-order vibrations have been found to be significant[19].The zeroth-order electromagnetic force is the primary vibration source[20].In Ref.[21],it was revealed that higher-order radial forces can generate lower-order radial forces and zeroth-order vibrations under a modulation effect.Moreover,the vibration was significant for the zeroth-order electromagnetic force at the slot number frequency[22].The vibration response was investigated for various orders of radial forces at slot number frequencies[23],which revealed that the slot-number-order radial force was the main vibration source.In addition,a teeth-chopping effect was proposed and explained theoretically.The slot number order radial force for an integral-slot PM machine was optimized to improve the vibration performance[24].However,most of the above studies were biased toward vibration reduction,resulting in an unacceptable drop in torque capability.Furthermore,the vibration of the integral-slot machine was adversely affected by the third harmonic of the PM magnetic field[12].Considering the mutually conflicting effect that the third harmonic exerts on the torque and vibration,multi-objective optimization was employed to avoid conflicts among the parameters.Furthermore,a substitute model with reliable accuracy is essential for improving the optimization efficiency,particularly for machines with various optimized parameters.Response surface models (RSM) have been widely employed to establish alternative models and improve optimization efficiency[25-27].

This study aims to improve the vibration and torque performance of an integral-slot SPM machine by adjusting the harmonic-injected PM shape,resulting in low vibration and high torque performance.The optimization goal includes several elements such as the average torque,torque ripple,and radial force.A multi-objective optimization method integrating the RSM and Barebones multi-objective particle swarm optimization (BB-MOPSO) algorithm was employed to enhance the global search capability and convergence rate.The remainder of this paper is organized as follows.In Section 2,the effects of the third harmonic injected into the sinusoidal PM shape on the vibration and torque performance of an integral-slot SPM machine are discussed.In Section 3,the RSM and BB-MOPSO algorithm are employed to optimize the harmonic-injected PM shape,and the superiority of the optimal machine is verified.In Section 4,a prototype is developed to verify the proposed method.Finally,the conclusions are presented in Section 5.

2 PM shape and performance analysis

2.1 Initial and eccentric PM machines

The electromagnetic performance of the 36-slot/12-pole integral-slot SPM machine,including the air-gap magnetic flux density,average torque,and torque ripple,is examined in this section.The geometry of the machine and its flux distribution at the rated load are illustrated in Fig.1.The primary parameters are listed in Tab.1.Fig.2 shows the structure of an eccentric PM,whereR1andR2are the circular radii of the initial and eccentric PM,respectively.Ois the circle center of the initial PM,O1is the external radius circle center of the PM when it is eccentric,his the eccentric distance,andhmaxis the maximum thickness of the PM.

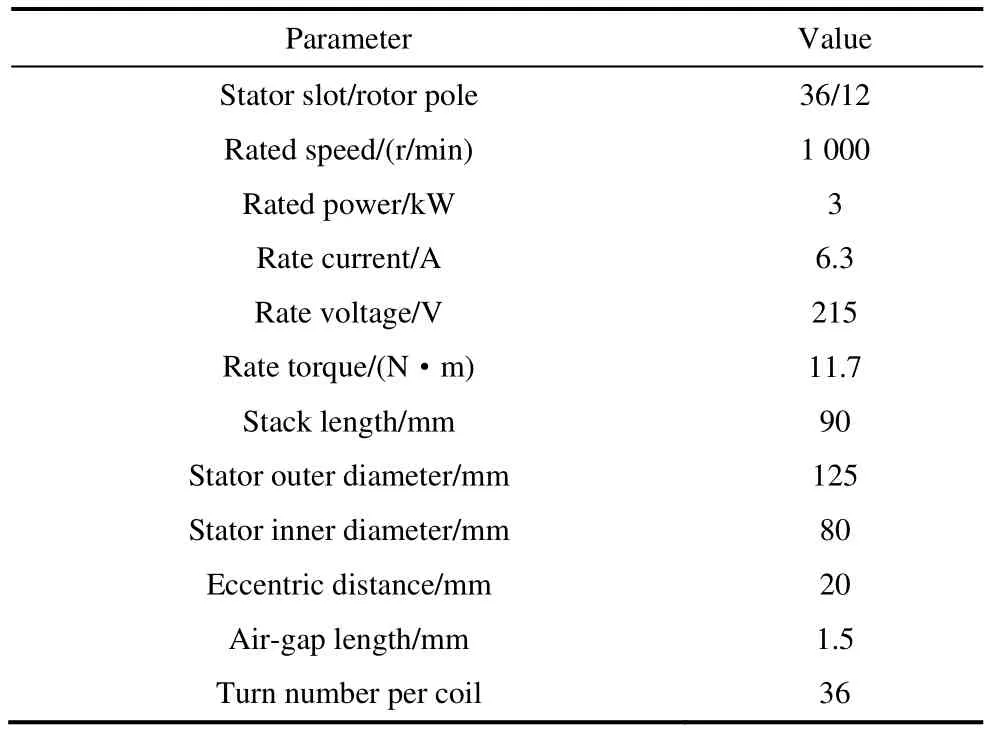
Tab.1 Main specifications of 36-slot/12-pole SPM machine

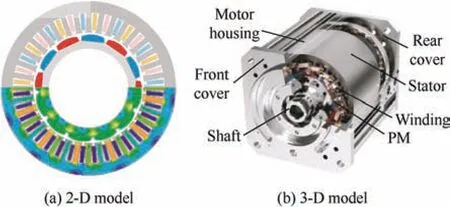
Fig.1 Geometry and flux distribution of 36-slot/12-pole SPM machine

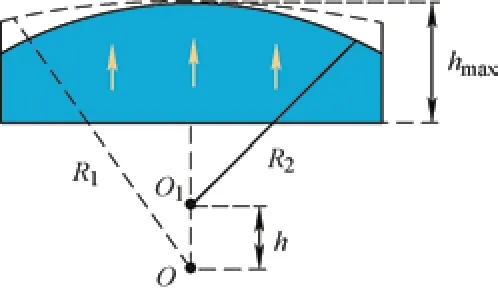
Fig.2 Eccentric PM structure

Generally,an eccentric PM can effectively reduce the torque ripple.Fig.3a shows the variation in torque performance with the eccentric distance.An eccentric distance of 20 mm exhibited a lower torque ripple than other distances when achieving the rated torque.Fig.3b shows the variation in the amplitude of thepth-and 3pth-order air-gap radial magnetic flux density harmonic components with the eccentricity distance.The amplitudes of thepthand 3pth-order components degraded with an increase in the eccentric distance.When the eccentric distance exceeded 20 mm,the 3pth-order components degraded,but the torque ripple suppressed slowly,even deteriorated after the eccentric distance of 22 mm.However,the average torque decreased significantly.Therefore,considering torque performance,the eccentric distance of the PM was selected as 20 mm.Fig.4 compares the air-gap radial magnetic flux density and harmonic content of the machines with those of the initial and eccentric PM.The eccentric PM machine presented a more sinusoidal waveform than the initial PM machine,derived from its lower harmonic content.

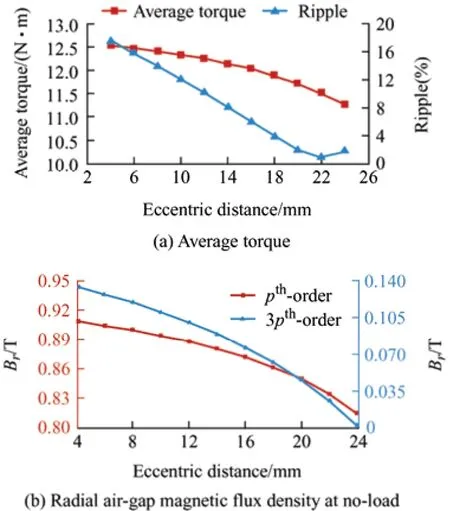
Fig.3 Varying machine performance based on eccentric distance of PM

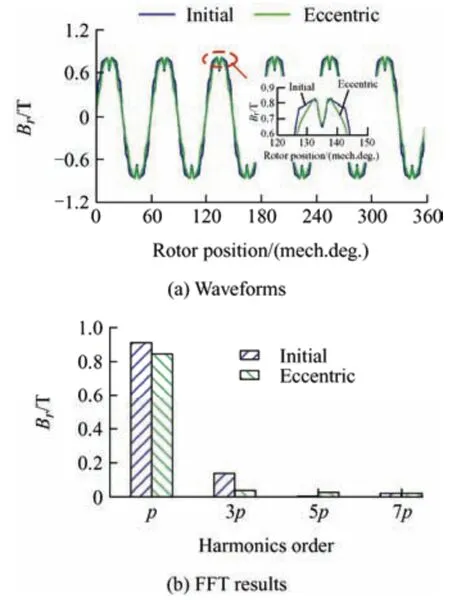
Fig.4 Radial air-gap magnetic flux density at no-load for initial and eccentric PM machines

Fig.5 shows the torque performance of both machines at a rated load of 1 000 r/min.The eccentric PM machine exhibited a low torque ripple,which is attributed to its reduced harmonic content.However,the fundamental amplitude diminished excessively,which reduced the average torque.

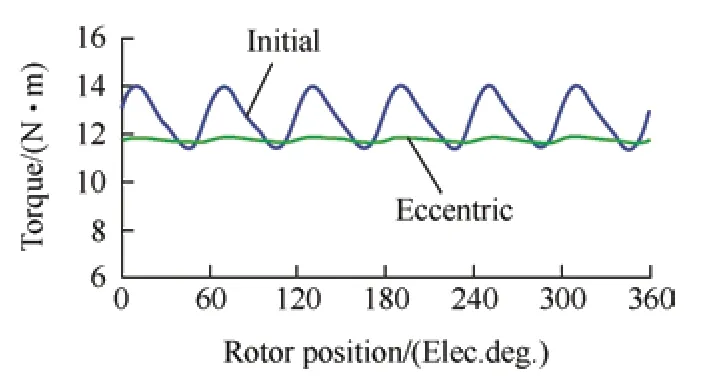
Fig.5 Torque performance of machines with initial and eccentric PM

A PM shaping with harmonic injection was adopted in this study to improve the torque performance of the machine.Details of this process are described in the following subsections.

2.2 Harmonic injected PM shape

Sine shaping with a third harmonic injected into the PM improves torque performance[14-15].To further strengthen the optimal harmonic amplitude,a PM shape based on a feedback function proposed in Ref.[16] was adopted,as shown in Fig.6.The feedback functionhm2(θ) can be described as

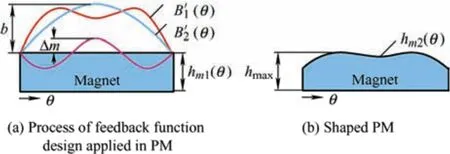
Fig.6 Feedback function design applied to PM

wherehm1(θ) is the thickness function of the initial PM,and its maximum value ishmax;B'1(θ) is the actual air-gap flux density function;B'2(θ) is the objective function in the optimization field;Brmis the remanence of the PM;lis the total length of the PM and air gap;Δmis intended to maintain the minimum air-gap lengthδairas constant;andμis an adjustment parameter to compensate for the slot effect.

By integrating Eq.(1) and the simulation,the amplitudes of the fundamental and adjustment coefficients were 1.8 and 0.3,respectively,achieving superior torque performance.However,the average torque loss was severe at 10.8 N·m.The third harmonic was injected into the PM to improve the average torque,and the torque performance variation withb3is shown in Fig.7.When the amplitude of the third harmonic reached 0.3,the average torque was maximized while maintaining a low torque ripple;therefore,it was selected as 0.3.The torque ripple remained in space for optimization,despite that the average torque was increased to 12.4 N·m.

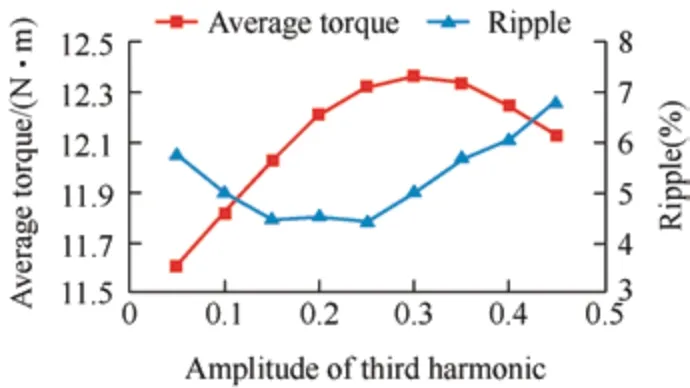
Fig.7 Torque performance based on the amplitude of the third harmonic

The selection process for these parameters was affected by subjective factors.Therefore,PM shaping with sine and third-harmonic injections(Sin+3rd-shaped PM machine) was carried out simultaneously in this study.The objective function can be expressed as

For further accuracy,the variation ranges of the fundamental harmonic,third harmonic,and compensation coefficients were limited to approximately those of the above single-parameter optimal values.Function Δm(b1,b3,μ) was derived by discretization and fitting,as expressed in Eq.(3).Their comprehensive optimal values were selected using a multiobjective algorithm,as introduced in Section 3,as follows

However,the effect of PM shaping with harmonic injection on the vibration performance of machines has not yet been investigated in previous studies.Therefore,this study investigated the comprehensive effect of the Sin+3rd-shaped PM machine on torque and vibration performance.

2.3 Radial force and vibration

As the tangential flux density is much smaller than the radial flux density,the tangential component is neglected when calculating the radial force.According to the Maxwell tensor method,the radial force density can be expressed as[28-29]

whereBris the radial air-gap magnetic flux density,BPMis the PM field air-gap magnetic flux density,BARMis the armature field air-gap magnetic flux density,andμ0is the vacuum permeability.

Tab.2 lists the spatial order and frequency of the radial force harmonics generated by the PM magnetic field self-interaction and the armature field interaction with the PM magnetic field.In Tab.2,Qis the number of stator slots,pis the number of rotor poles,Fmis the amplitude of themth-order PM magnetomotive force,Fνis the amplitude of theνth-order armature magnetomotive force,Λ0is the DC component of the air-gap permeance,andΛkis theνth-order air-gap permeance.

Tab.2 Radial force harmonics distribution

The vibration displacementYminduced by different orders of radial force can be described as

whereRyis the average radius of the stator yoke,Rsis the stator inner diameter,Eis the Young’s modulus,Tyis the thickness of the stator yoke,andFis themth-order radial force amplitude.Ymis a linear variable withF.Whenm≥2,Ymis approximately and inversely proportional to the fourth power ofm.Ym=0/Ym≥2increases withm,reflecting a more significant zeroth-order deformation for a more prominentm.

Based on Tab.2 and Eq.(5),increasing the third-harmonic amplitude of the PM magnetic field can deteriorate the zeroth-order vibration in a 36-slot/12-pole SPM machine.Fig.8a shows the simulated vibration acceleration of this machine,with its peak value emerging at 6fand 12f,which proves its main vibration sources at these two frequencies.A 2D fast Fourier transformation (FFT) of the radial force for the initial machine was performed,and the results are shown in Fig.8b.The magnitudes of the 36th-order radial force at 6fand the 72th-order radial force at 12fwere the largest.Consequently,the (36,6f)thand(72,12f)thradial forces were the main sources of the zeroth-order vibration of this machine,and its vibration response could be improved by decreasing the amplitudes.

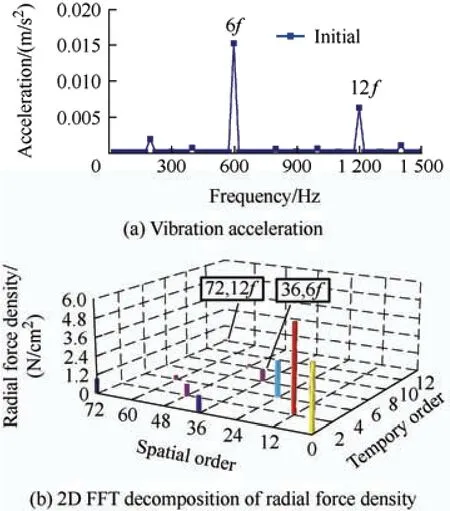
Fig.8 Finite-element results of vibration acceleration and radial force density of the initial machine

3 Optimization and performance evaluation

The RSM was applied to construct a substitute model for the machine.Moreover,to eliminate the impact of the subjective factors such as the weight coefficients,the BB-MOPSO algorithm was employed to solve the optimization problem.The workflow chart is shown in Fig.9.

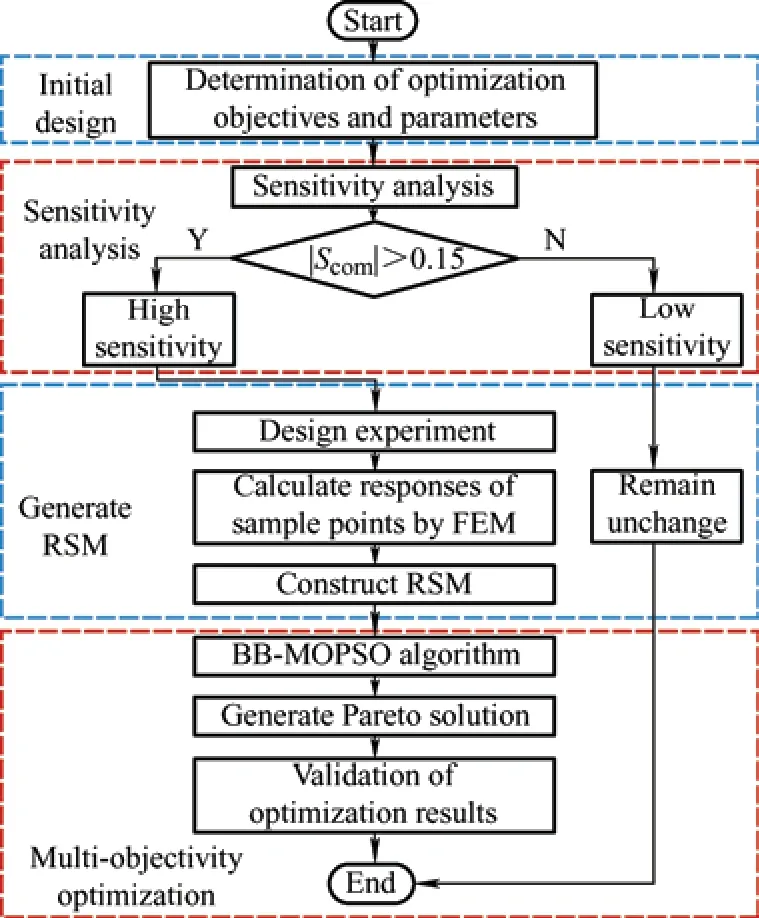
Fig.9 Complete process of multi-objective optimization

3.1 Sensitivity analysis

The effect of the third-harmonic amplitude of the PM magnetic field on the torque and vibration performance was contradictory in integral-slot SPM machines.Moreover,the sources of the zeroth-order vibrations were the (36,6f)thand (72,12f)thradial forces.Consequently,to obtain the optimal torque and vibration performance,the average torque,torque ripple,(36,6f)thradial force,and (72,12f)thradial force were considered as optimization objectives.Eight parameters were selected as optimization variables,such asBs0,as listed in Tab.3.

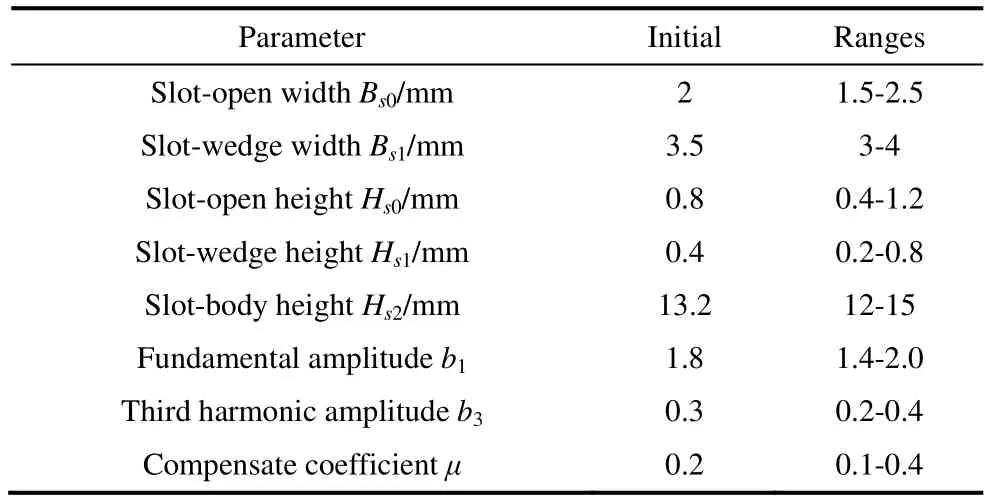
Tab.3 Initial sizes and ranges of variation for design variables

The sensitivity of the design variables is defined as

whereydenotes the optimization objective,E(y|xn)indicates the average value ofywith constantx,andV(E(y|xn)) andV(y) are the variances ofE(y|xn) andy,respectively.

These eight variables were captured using a definitive screening design to generate 17 samples,which substantially reduced the computational cost of the sensitivity analysis.This approach can capture the non-linearity of these variables,while avoiding their coupling effects.However,each variable exhibited a distinct degree of influence on different objectives.Consequently,comprehensive sensitivity was employed to assess the significance of each variable,which can be defined as

whereλkis the weight of thekthoptimization target.In this work,λ1=λ2=λ3=λ4=0.25 was designed to reduce the influence of subjective factors.

Based on Eqs.(6)-(8),the results of the sensitivity calculations are summarized in Tab.4.To visually distinguish the sensitivities of the different variables,these data are shown in Fig.10.It is apparent that the fundamental harmonic,third harmonic,and compensation coefficients exhibited a slightly higher sensitivity than the others variable.Therefore,these variables were selected as the optimization variables for multi-objective optimization.

Tab.4 Sensitivities of design variables

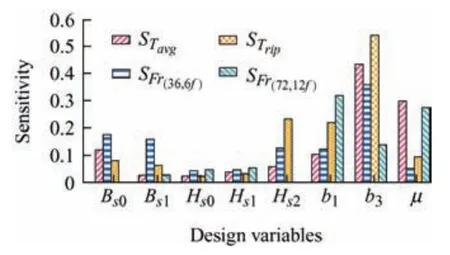
Fig.10 Sensitivity with different optimization objectives

3.2 Mathematical models based on RSM

In this study,the RSM was used to construct an alternative model to further reduce the computational burden.The Box-Behnken design is a classical method used to establish an RSM.The sample point distribution of the Box-Behnken design with three design variables is shown in Fig.11.The simulation results were analyzed,and the corresponding polynomial regression model can be expressed as

Fig.11 Samples distribution of Box-Behnken design with three design variables

whereχiis theithofnvariables;χ,a0,ai,andajare the regression coefficients;andεis the random error.

The RSM fitting accuracy is essential to obtain reliable optimization results.The determination coefficientR2is typically used to assess the fitting accuracy of the RSM,and is defined as

whereβis the number of samples,ρiis the response value,is the estimated value,andis the average value of the responses.

Fig.12 shows the partial RSM of the fundamental harmonic,third harmonic,and compensation coefficients.The determination coefficients of all RSM were larger than 0.9,indicating that the fitting accuracy satisfied the requirement and had a high reliability.According to the RSM,the regression equations for the average torqueTavg,torque rippleTrip,(36,6f)thradial force,and (72,12f)thradial force were fitted using Eqs.(11)-(14).Because various variables were nonlinearly associated with the objectives,identifying the optimal values through subjective judgment was difficult.Therefore,a compromise design using a multi-objective optimization algorithm was used.

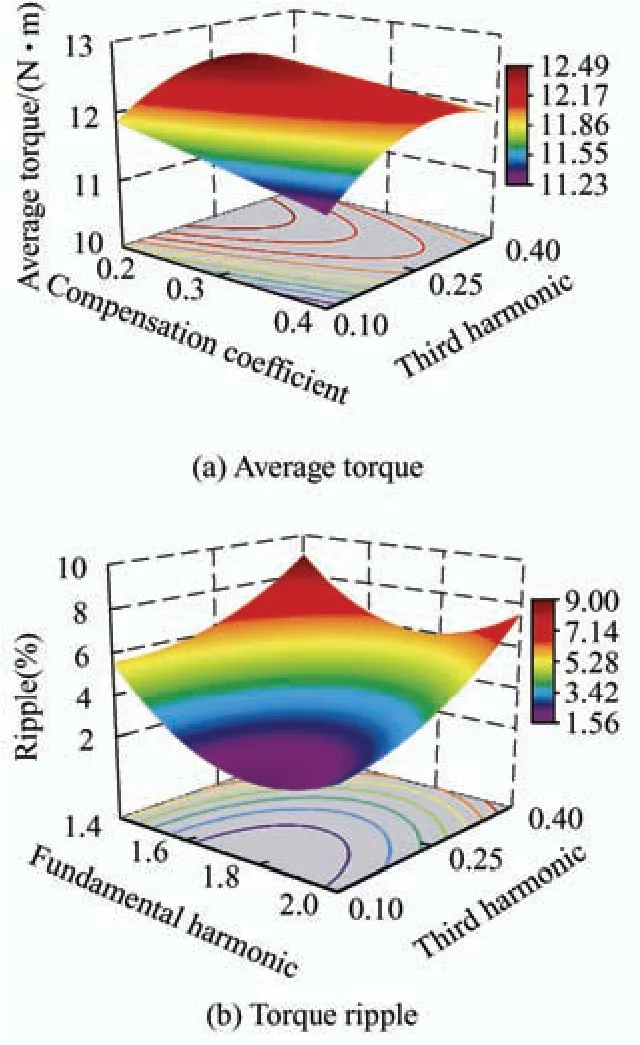
Fig.12 Response surface on b1,b3,and μ

3.3 Optimization based on BB-MOPSO

The BB-MOPSO algorithm is based on a particle-updating strategy in which no control parameters need to be adjusted.It employed a time-varying mutation operator to expand its search capability[30].The particle update formula is defined as follows

wherekis an arbitrary number within [0,1],Lim,n(x)andLgm,n(x) indicate the individual and global optimal locations,respectively.

Therefore,the BB-MOPSO algorithm was combined with the RSM to quickly optimize the above highly sensitive variables.The multi-objective optimization function and constraints,which must be satisfied,are as follows

whereβ1,β2,β3,andβ4are the weight coefficients of the average torqueTavg,torque rippleTrip,(36,6f)thradial force,and (72,12f)thradial force,respectively.To balance the machine performance,β1,β2,β3,andβ4are given as 0.25.

Fig.13 shows the Pareto front with respect to the average torque,torque ripple,and (36,6f)thradial force.A contradiction between the objectives is evident.The optimal trade-off solution is marked by black,considering the machine performance requirements comprehensively from the Pareto solutions.The machine performance of sine shaping with an optimal third harmonic was substantially improved compared with that of the initial machine.

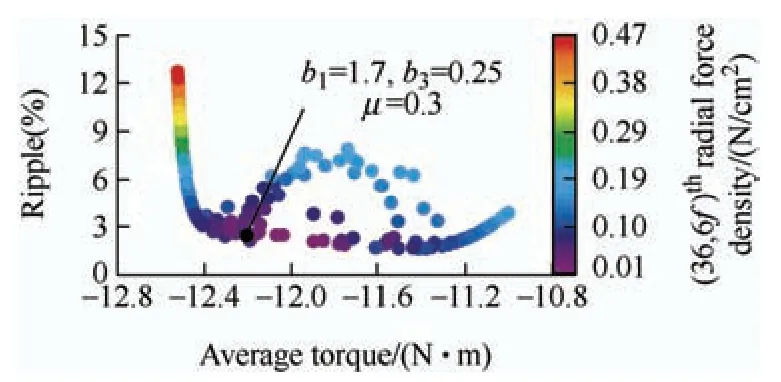
Fig.13 Pareto optimal solutions of BB-MOPSO algorithm optimization

3.4 Performance evaluation

Fig.14 compares three different PM shapes,all of which maintain the principle of a constant minimum air gap length.The no-load air-gap flux harmonics and torque performance are shown in Fig.15.The average torque of the Sin+3rd-shaped PM machine was 12.2 N·m,which was 4.0% higher than the eccentric PM machine with 11.7 N·m,and the initial machine with 12.6 N·m (100%).Meanwhile,the torque ripple of the initial one was 20.7%,and both the optimal and eccentric PM machines was reduced to 2.9% and 2.1%,respectively.In Fig.2,one machine with an eccentric distance of 12.2 mm provides a comparable average torque;however,the torque ripple increases unacceptably to 9.7%.The superior torque performance of the optimal Sin+3rd-shaped PM machine was derived from the fact that its fundamental and third-harmonic levels are higher than those of an eccentric machine.

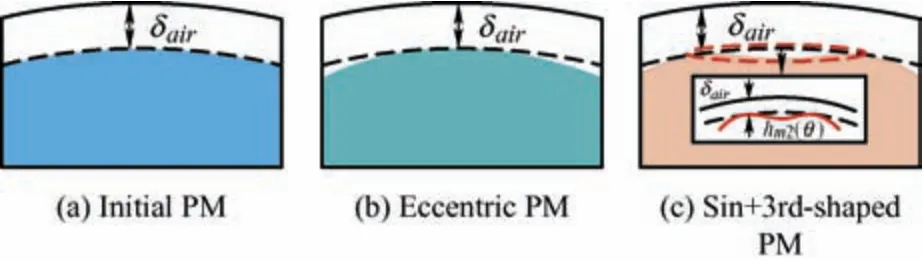
Fig.14 Comparison of different PM shapes

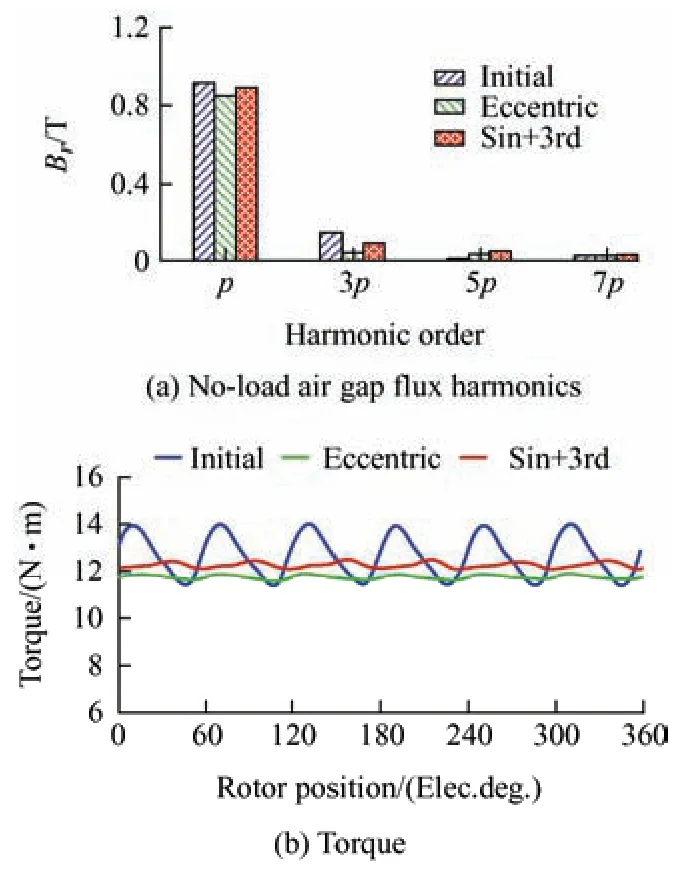
Fig.15 Comparison of the air-gap magnetic flux and torque waveform

Fig.16 shows the 2D FFT of the radial force and vibration acceleration of the three machines.The(36,6f)thand (72,12f)thradial force amplitudes of machines with eccentric and Sin+3rd-shaped PM decreased,and the vibration performance improved.The vibration acceleration of the third-harmonicshaped PM machine at 6fand 12fdecreased from 0.15 m/s2to 0.006 m/s2and 0.006 m/s2to 0.003 m/s2,respectively.The vibration performance of the Sin+3rd-shaped PM machine improved significantly and was almost identical to that of the eccentric machine.Regarding the torque and vibration performance,the Sin+3rd-shaped PM machine was superior and more favorable than the eccentric machine.It was demonstrated that the PM shaping technique with a third harmonic can effectively improve the torque and vibration performance of an integral-slot SPM machine.

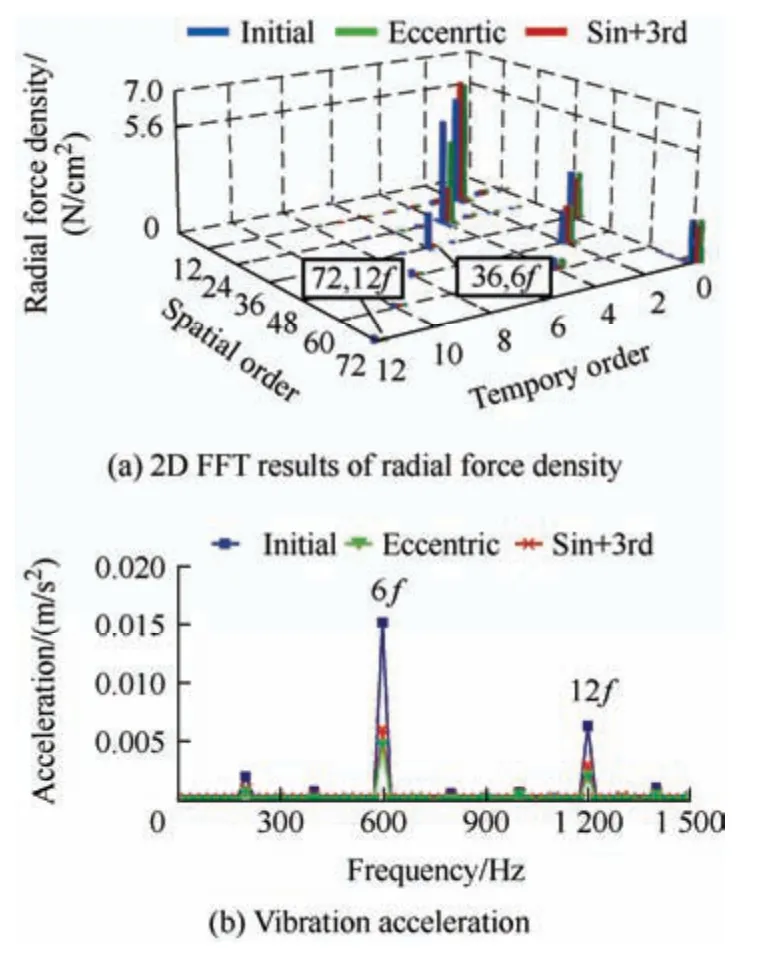
Fig.16 Comparison of radial force and vibration acceleration

4 Experimental validation

A 36-slot/12-pole integral-slot SPM machine with an eccentric PM was manufactured and tested to verify the theoretical analysis.Fig.17a presents its prototype.Fig.17b shows the modal experiments on the stator,stator with coils,and casing.First,a flexible rope was suspended from the stator assembly to simulate unconstrained conditions.Subsequently,several accelerometers were simultaneously installed at different locations on the housing surface to facilitate an accurate acceleration response.The simulation and measurement results of the modal data are summarized in Tab.5.Because the frequency response measured using the excitation method was limited to 8 kHz,a high modal could not be measured.Thus,the high modal parameters originated from the simulation results.

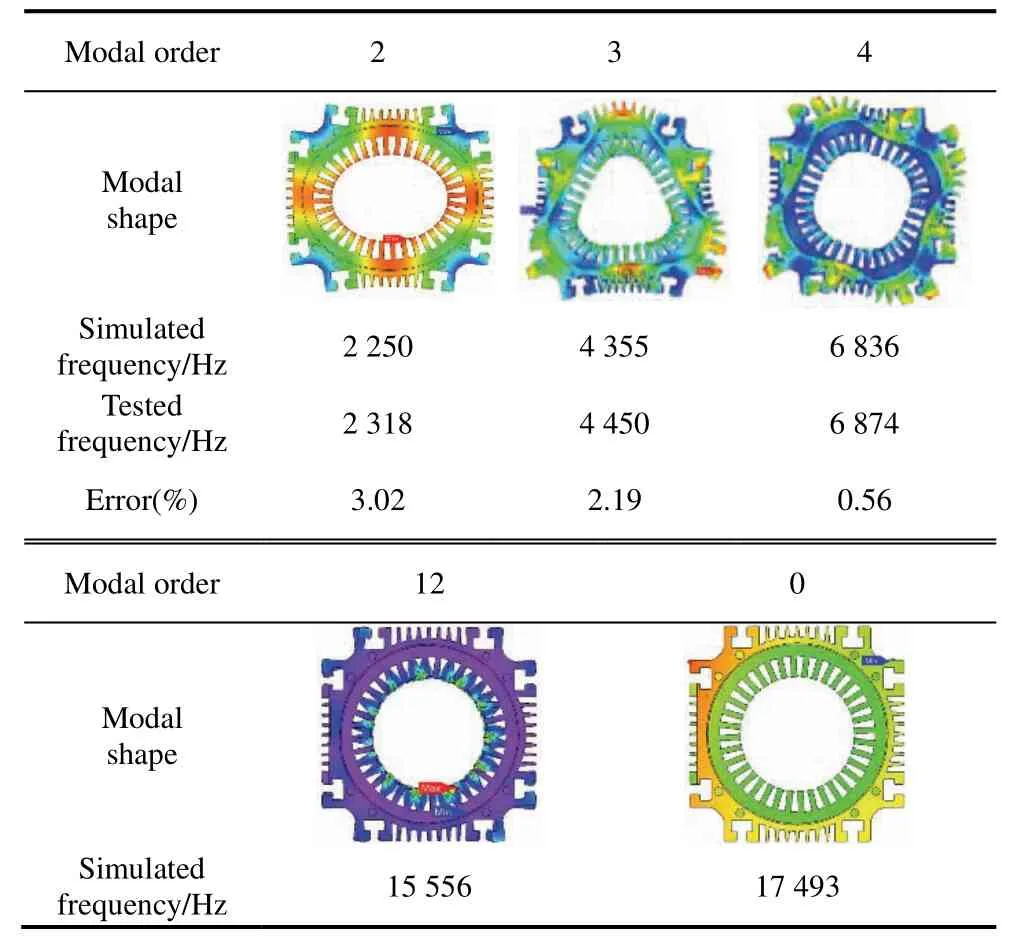
Tab.5 Modal parameters

Fig.17 SPM prototype and modal test

Fig.18 shows the experimental platform of the prototype.The simulated and measured no-load back-EMF waveforms at 1 000 r/min are shown in Fig.19.The measured results agree with the simulated results.Fig.20a shows the measured three-phase current and torque waveforms at a rated load of 1 000 r/min.The current amplitude was 6.3 A,and the measured average torque was approximately 9.7 N·m with a torque ripple of 4.6%.Fig.20b shows the simulated and measured vibration accelerations,and the peaks emerged at 6fand 12f,which is consistent with the simulation and theoretical analysis.The torque performances at different current amplitudes are compared in Fig.21.The optimal third-harmonic-shaped PM machine displayed superior torque performance.A slight increase in the torque ripple during the experiment was observed,which was attributed to the average torque deficit.A slight difference between the simulation and the measurement was observed,but it was within an acceptable range.

Fig.18 Test experiment platform

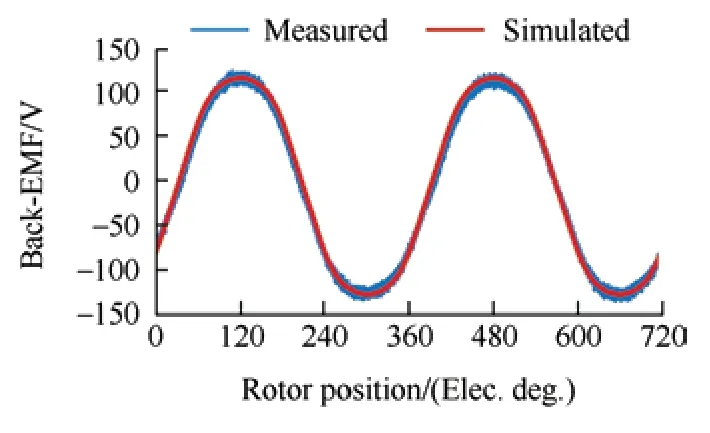
Fig.19 Comparison of simulated and measured no-load back-EMF at 1 000 r/min

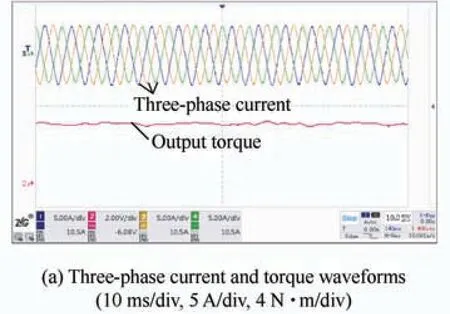
Fig.20 Comparison of predicted and experimental data at rated load

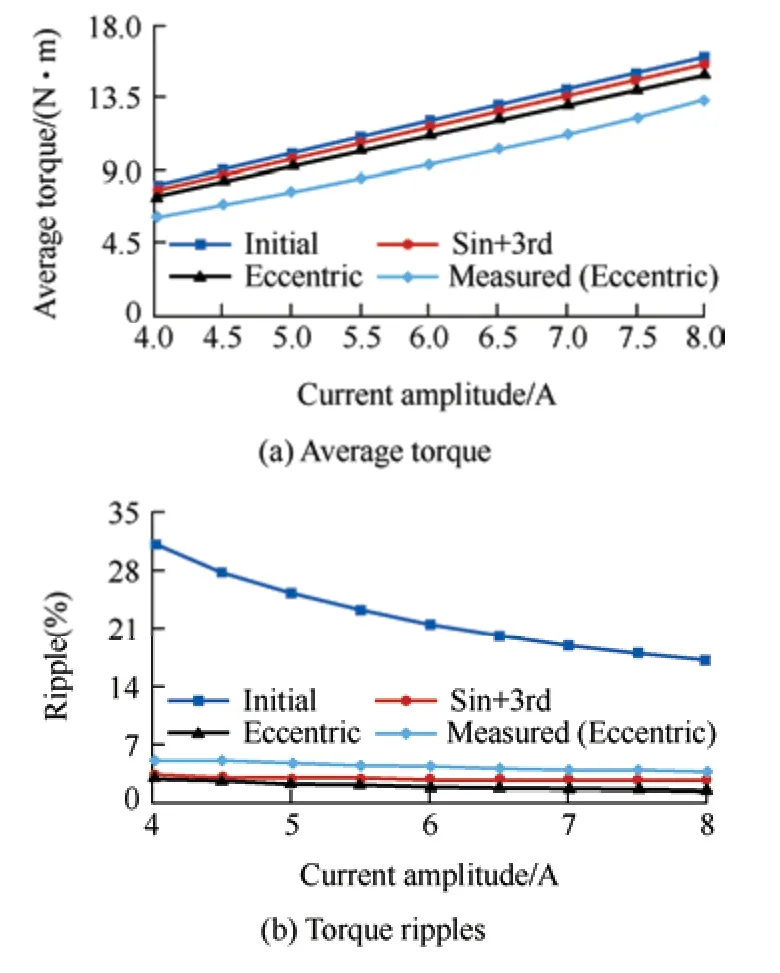
Fig.21 Comparison of torque performance with different current amplitudes

5 Conclusions

This study investigated a Sin+3rd-shaped PM to improve the vibration and torque performance of an integral-slot SPM machine.First,the effects of the third harmonic of the PM magnetic field on the vibration and torque performance of an integral-slot SPM machine were studied.The Sin+3rd-shaped PM was found to have a contrary effect on the vibration and torque performance.The RSM and BB-MOPSO algorithms were then employed to optimize the harmonic-injected PM shape to improve the vibration and torque performance.The performance advantages of a 36-slot/12-pole SPM machine with an optimal Sin+3rd-shaped PM were verified.The machine was characterized by a high average torque,low torque ripple,and low vibration response.The average torque of the optimal Sin+3rd-shaped PM machine was enhanced by 4% to 12.2 N·m compared with the eccentric PM machine.The torque ripple was reduced by 10% using an eccentric PM machine with the same torque capability.In addition,the vibration performance was as excellent as that of a machine with an eccentric distance of 16 mm.Finally,an eccentric PM prototype was fabricated and measured,and the results indicate that the experimental and simulation data are in good agreement.Future work will involve the fabrication and testing of a prototype of the Sin+3rd-shaped PM to verify the theoretical analysis.This method is not constrained to the machine used in this study and can be applied to various SPM machines for vibration and torque improvement.