基于电气特性分析的中压配电网拓扑变动分段辨识*
2024-01-15杨舒航李诗伟吴红斌蒋思成魏英杰
杨舒航 李诗伟 吴红斌 蒋思成 魏英杰
(1.合肥工业大学新能源利用与节能安徽省重点实验室 合肥 230009;2.国网上海浦东供电公司 上海 200120)
1 引言
近年来,风、光等大量分布式电源(Distributed generation,DG)的接入[1-2],显著改变了传统配电网的电气特性,给配电网安全、稳定、经济运行提出了更高的要求[3]。为了应对电气特性的复杂化,配电网需要不断进行网络重构以保证最优化运行[4],且拓扑结构又是进行配电网状态估计、网络重构、网络最优化运行等工作的基础[5-8],所以进行配电网拓扑结构辨识研究十分必要。而配电网中线路、节点众多,量测装置不能完全覆盖,在量测数据不足和大量分布式电源接入时进行拓扑结构辨识面临诸多挑战。
现有的配电网拓扑结构辨识方法可以分为几类。一是基于电压相关性分析的方法,文献[9-10]通过计算任意两节点间的电压互信息值,根据互信息值最大的两个节点之间存在实际连接识别配电网拓扑结构;文献[11]通过节点注入功率计算支路电压偏差的方差,根据电压偏差方差最小识别节点间连接关系,进而实现拓扑结构辨识。但是,在电压量测数据不齐全的配电网中利用节点电压信息的方法识别整个拓扑结构可能存在困难[12-13]。
二是通过智能终端(Smart terminal unit,STU)的信息交互进行拓扑识别的方法,文献[14-15]通过安装在配电网开关断路器上智能终端间的信息交互,逐级查询识别配电网拓扑结构。文献[16]通过STU 自身配置范围内的局部搜索和与相邻STU 的跨拓扑片搜索识别拓扑结构。利用智能终端信息交互的方法辨识拓扑结构,需要在配电网安装新的硬件装置,相较于软件识别的方法增加了识别成本,经济性较差。
近年来人工智能领域的图卷积网络[17]、贝叶斯网络[18]、蝠鲼觅食算法[19]等机器学习方法也成为了解决这一问题的研究热点。文献[17-18]利用电压、功率量测数据,综合所有可能的拓扑结构建立机器学习模型,通过学习模型与实际量测数据拟合程度的对比识别最有可能的拓扑结构。文献[19]利用改进的蝠鲼觅食优化支持向量机的方法,对配电网电压数据的训练集和拓扑辨识模型进行了优化。以上基于神经网络、人工智能的方法在本质上仍然属于拓扑库对比,对于分布式电源接入下电气数据瞬息万变的配电网,辨识效果可能不佳。
综上所述,现有的配电网拓扑结构辨识方法存在以下问题:① 现有的配电网拓扑结构辨识方法往往是对整个拓扑所有节点、线路的连接关系进行全部重新识别,而实际配电网拓扑的优化重构和线路故障后的重构往往只是部分拓扑结构发生改变,现有的方法对拓扑未发生改变的部分进行重复识别,使得拓扑辨识效率大大降低;② 由于电压量测装置不能覆盖配电网的所有线路、节点,现有的大量依靠配电网完整电压量测数据进行拓扑结构辨识的方法缺乏实用意义;③ 近年来分布式电源的大量接入改变了传统配电网的电气特性。分布式电源向配电网输送的功率抬升了接入点的电压,有些线路的潮流方向甚至发生改变。这些变化使得一些基于传统配电网的拓扑辨识方法出现识别错误,甚至失效。
针对以上问题,本文在分析配电网节点注入功率变化的基础上,结合“超节点”的概念,提出了识别拓扑改变部分的方法。在此基础上,通过对分布式电源接入前后的配电网功率传输特性和节点电压幅值特性的分析,提出了分段线路、末段线路以及分段线路连接的拓扑结构辨识方法。最后利用算例系统进行了仿真验证。本文的主要研究内容和创新点如下所示。
(1) 通过引入“超节点”概念,基于节点注入功率变化,本文提出了拓扑变化部分的识别方法。该方法不仅能对拓扑的改变进行识别,还能识别出拓扑的改变部分。通过对拓扑改变的部分进行识别,避免了对拓扑未改变部分的重复识别,提高了拓扑辨识效率。
(2) 通过对分布式电源接入前后配电网电气特性的分析,本文提出了变动拓扑的分段辨识方法。该方法仅需采集分段点和末节点的电压量测数据,解决了传统拓扑辨识方法对完整电压量测数据的依赖,很好地适应了配电网电压量测数据不足的现状,提高了方法的实用性。
(3) 本文方法基于分布式电源接入配电网前后的电气特性分析提出,在分布式电源接入时仍能够有效对拓扑结构进行辨识。
2 DG 接入前后配电网电气特性分析
2.1 DG 接入后功率和电压变化情况
IEEE-33 算例系统如图1 所示,无DG 接入时,节点注入功率和电压幅值沿配电线路递减[20];当节点8、15 加入DG,功率传输呈现分段递减特性,且DG 接入抬升了接入点8、15 的电压幅值,节点电压不再呈现递减变化特性,仿真结果如图2 所示。
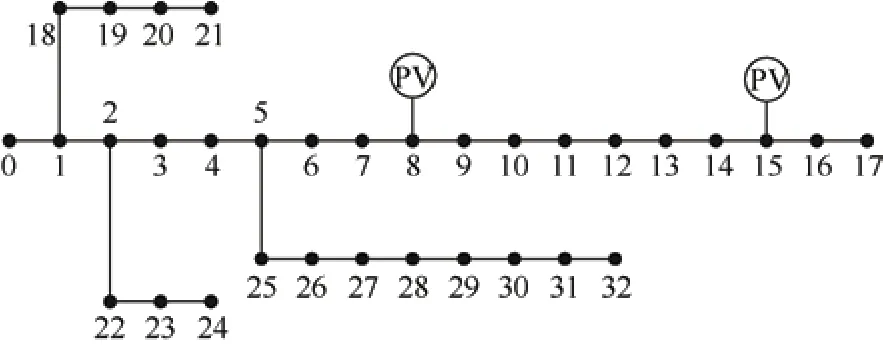
图1 IEEE-33 配电网系统

图2 DG 接入前后电气特性的变化
2.2 功率传输特性
如图2a 所示,分布式电源的接入改变了配电网的功率传输特性。分布式电源为接入节点提供了部分所需负荷,节点注入功率减小;上游节点由于受到分布式电源接入的影响,节点注入功率同样减小,减小数值近似等于分布式电源向配电网输送功率;下游节点的注入功率不变。此时分布式电源接入节点的注入功率可能小于与之直接相连的下游节点的注入功率。节点注入功率将不再沿配电线路连续递减,而变为分段连续递减,分段点为分布式电源接入节点。
2.3 电压幅值特性
如图2b 所示,在没有分布式电源接入时,从配电网首节点出发,由于配电线路存在电压损耗,节点电压幅值将沿配电线路连续递减。
分布式电源的接入改变了配电网的节点电压幅值特性。分布式电源的接入抬升了节点电压,使得接入节点的电压幅值可能高于附近节点的电压幅值,此时节点电压幅值将不再遵循沿配电线路递减的特性。
3 基于“超节点”的拓扑变化识别
3.1 超节点
根据基尔霍夫电流定律,流入某节点的电流等于流出该节点的电流[21]。将图3 中虚线内的4 个节点及其线路视为1 个节点,该节点仍然满足基尔霍夫电流定律,即为“超节点”。

图3 “超节点”
将“超节点”的概念延伸至配电网,如图4 所示,此时输入、输出电流变为节点注入、流出功率。节点注入功率如式(1)所示
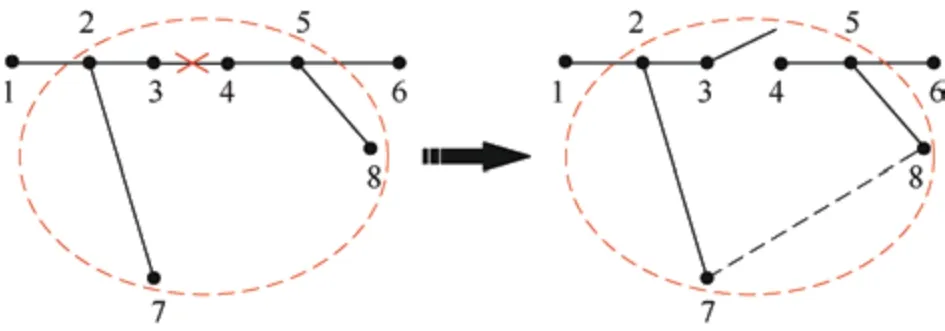
图4 联络线投入
式中,S为节点注入功率;U为节点电压,I*为节点注入电流的共轭;p为节点注入有功功率,q为节点注入无功功率;节点流出功率与此类似。
当拓扑结构改变时,节点间上下游关系随之改变,节点注入功率显著变化。虽然用户负荷会随时间发生变化,但其远远小于拓扑结构改变带来的节点注入功率变化。即对于配电网中的一个“超节点”而言,无论超节点内部线路连接、供配电关系如何改变,注入、流出超节点的功率近似不变。以节点注入有功功率为例,即
式中,Δpin、Δpout为拓扑变化前后,注入、流出超节点的有功功率变化量。
3.2 节点注入功率变化
3.2.1 超节点内外节点的注入功率变化
我国配电网一般是以“闭环设计、开环运行”为运行方式的辐射状网络,当出现短路故障导致线路断开时,与断开线路及其附近线路形成环路的联络线投入使用,为断开线路的下游线路供电。
如图4 所示,节点3-4 间拓扑变化时断开线路,节点3、4 成为末节点,故注入功率显著减少。联络线7-8 投入,为断开线路的下游节点恢复供电;联络线上的7、8 节点新增下游线路,故节点注入功率显著增加。此时,状态改变支路3-4 与投入联络线7-8 所在的非闭合环路中,所有支路(2-3、2-7、3-4、4-5、5-8、7-8)的传输功率均发生改变。
将支路3-4 与投入联络线7-8 所在的非闭合环路(即图4 中虚线内的部分)视为一个超节点,根据第3.1 节的分析可知,此时该“超节点”外的节点1、6 及其支路1-2、5-6,其节点注入功率和支路传输功率不变。
综上,将注入功率改变的节点及其支路形成的非闭合回路视为一个超节点,图4 中虚线内的部分即为一个超节点。以有功功率为例有
式中,i为节点注入功率改变的节点。
3.2.2 线路功率损耗对节点注入功率的影响
某节点的注入功率由该节点及下游节点所带负荷和线路功率损耗两部分组成
式中,Si为某节点及下游节点负荷功率;Sloss为线路损耗功率。
拓扑改变后,整个网络的线路功率损耗随之改变。将注入功率变化的节点及其支路视为一个超节点,根据超节点概念,此时注入、流出超节点的功率近似不变,即超节点内部节点的注入功率变化对其外部节点的注入功率没有影响。此时,由式(4)可知,对于超节点的外部节点,其注入功率将随线路损耗功率变化而变化,但该变化量远远小于拓扑改变部分的节点(即超节点内部的节点)注入功率变化,故忽略线路功率损耗对节点注入功率的影响。
3.3 拓扑变化识别判据
拓扑改变后,超节点外部节点的注入功率近似不变,超节点内部节点的注入功率显著变化。
以有功功率为例,提出基于节点注入功率变化的拓扑变化识别判据如下
式中,i为注入功率改变的节点,j为注入功率不变的节点,V为超节点。
使用拓扑变化识别判据遍历所有节点,将所有注入功率变化的节点归于超节点中,确定开关状态发生变化的支路所在的拓扑范围。使用无功功率进行判断与此类似。判据不仅能对配电网拓扑结构改变进行识别,还能将状态变化的支路范围缩小至节点注入功率改变的超节点中,降低了辨识拓扑的复杂度,缩短了辨识所需时间。而由于判据基于拓扑改变前后节点注入功率变化,故DG 接入带来的配电网电压、功率特性变化不会对本文所提方法造成影响。
配电网中,拓扑结构会根据配电网的电压质量,最优化运行条件等进行合理重构、调整。中压配电网的拓扑结构虽然变化频繁,但拓扑结构的变化往往只是局部节点连接关系的变化。故本文在辨识拓扑结构时,仅对发生改变的拓扑进行辨识,对未发生变化的拓扑部分不予识别,这避免了对未改变拓扑的重复识别,大幅度提升了识别效率。
4 拓扑结构分段辨识
4.1 分段线路识别
对于配电网中的绝大部分节点,其节点度数为2,即一个节点有两个相邻节点。当配电网无DG 接入时,节点注入功率沿线路递减。此时,与某一节点注入功率差值绝对值最小的节点,位于其相邻节点中,故可根据相邻节点的注入功率差值绝对值最小对节点间的连接关系进行识别。
然而对于大负荷节点而言,传输功率在经过该节点时将产生明显跌落,此时根据注入功率差值绝对值最小对节点连接关系进行判断,将不能识别大负荷节点与其下游节点的连接,识别结果呈现分段特性。而DG 接入时,DG 为接入点提供了部分负荷功率,接入节点的注入功率骤降,DG 接入点与上游节点的注入功率产生断层。此时,根据注入有功、无功功率差值绝对值最小对节点连接关系进行判断,同样不能识别DG 接入节点与其上游节点的连接,识别结果同样呈现分段特性。
综上,本文根据相邻节点注入有功、无功差值绝对值最小这一特性,对有无DG 接入的配电网拓扑进行分段识别
式中,V1为拓扑改变部分的节点集合;pi、pj为集合中任意两节点的注入有功功率;qi、qj为注入无功功率。
对于分段线路中的任意两相邻节点A、B,以及与它们相邻的两节点C、D,四个节点的连接关系如图5 所示。

图5 四节点连接关系
节点A、B与其他节点的注入功率差值有以下3种情况。
(1)A、B互为注入功率差值最小节点。
(2)A的注入功率差值最小节点为B,B的注入功率差值次最小节点为A,B的注入功率差值最小节点为D。或B的注入功率差值最小节点为A,A的注入功率差值次最小节点为B,A的注入功率差值最小节点为C。
(3)A的注入功率差值最小节点为C,B的注入功率差值最小节点为D,A、B互为注入功率差值次最小节点。
基于以上3 种情况,提出双重验证和补充识别的分段线路识别方法。对于符合情况(1)、(2)的节点进行双重验证。
(1) 双重验证:对于集合中的任意节点a,计算出与a注入功率差值最小的节点b,如果与b注入功率差值最小和次最小的两个节点中同样包含a,则a、b两节点存在连接关系。
对于符合情况(3)的节点进行补充识别。
(2) 补充识别:提取双重验证识别出的分段线路首、末节点,互为次最小值的两节点存在连接关系。
补充识别解决了相邻节点互为注入功率差值次最小节点时的连接关系识别困难的问题,提高了拓扑结构辨识准确度。对于度数大于2 的枢纽节点,可能不能识别出它的所有相邻节点,剩余节点可通过第4.3 节分段线路连接进行识别。
4.2 末段线路识别
分段线路识别初步完成了对拓扑结构的分段识别,如图6 所示。分段线路识别将图6a 的实际网络拓扑以图6b 的多条分段线路形式识别出,图6b 中虚线表示分段线路间未识别出的连接线路,需要通过后续第4.3 节提出的方法对分段线路间的连接进行识别。

图6 末节点连接关系识别错误
对比图6a 的实际网络拓扑和图6b 的分段线路识别结果可以看出,由于末节点的注入功率仅为其节点所带的负荷功率,而不同分段线路的末节点的负荷功率可能相等或接近,故仅通过基于功率传输特性的分段线路识别辨识出的末段线路,可能会出现不同分段线路的末节点之间错误相连的情况。从图6 可知,可能结果1 中的9-10-5-8-11、结果2 中的4-11-8-5 这两条末段线路中的末节点连接关系均存在错误,故需要对末节点所在的末段线路中的节点连接关系进行校正识别。
对联络线和最小注入功率节点所在分段线路(末节点所在分段线路)中的节点连接关系进行二次辨识时,通过电压幅值差值绝对值最小的两节点直接相连这一特性,对节点连接关系进行识别
式中,V2为末段线路的节点集合;|Ui|、|Uj|为集合中任意两节点的电压幅值。末段线路识别算法流程如下所示。
步骤1:提取联络线节点和最小注入功率节点所在的分段线路,将该分段线路中的节点归于集合V2,从微型同步相量测量单元获取节点电压量测数据。
步骤2:根据式(7),计算集合V2中每个节点与其他节点的电压幅值差值绝对值,将计算结果降序排序并保留每组的最后两个节点。
步骤3:用电压幅值差值绝对值替换注入功率差值绝对值,使用双重验证和补充识别对末段线路进行二次辨识。
对于电压等级相同的相邻线路,其节点电压幅值可能相近;但由于线路长度一般不同,所以不同线路的末节点电压幅值一般不会相近,故使用节点电压幅值特性可以正确识别末节点连接关系。二次辨识对末节点连接关系进行了校正,提高了拓扑结构辨识准确度。
4.3 分段线路连接识别
完成分段线路识别和末段线路识别后,为了获得完整的配电网拓扑结构,需要对分段线路间的连接关系进行识别。提取分段线路首、末节点电压幅值,分段线路通过电压幅值差值绝对值最小的两个节点相连
式中,V3为所有分段线路首、末节点的集合。
将已识别出连接关系的节点从集合中剔除,重新对剩余节点进行识别。为了避免出现线路成环、配电网闭环运行的识别结果错误,当集合中只剩两个节点时终止循环迭代,完成分段线路连接识别。
由于不同线路的分段结果一般不同,且仅对分段线路首、末节点的电压幅值进行了比较,故不会出现因相邻线路电压等级相同致使分段线路连接识别错误的情况。
分段线路连接识别和末段线路识别只需要获得分段线路首、末节点和末段线路节点的电压量测数据,在配电网量测不足的情况下仍能有效辨识拓扑结构。
4.4 量测数据的配合
节点注入功率和节点电压数据分别通过SCADA和μPMU 量测系统获得[22]。SCADA 量测系统采集配电网数据一般以分钟为频度,拓扑变化速率一般为分钟级,故直接使用SCADA 量测系统每分钟采集的节点注入功率数据即可。μPMU 装置采样频率高,一般为毫秒级,可以精确量测节点的电压、电流的幅值和相位。使用SCADA 量测装置采集1 min 和2 min 时刻的系统所有节点的注入功率P1、Q1、P2、Q2,并计算两个相邻时刻的节点注入功率差值。当2 min 时刻系统部分节点的注入功率发生变化时,根据拓扑变化识别判据可知,拓扑结构发生改变,且发生改变的时刻为1~2 min。此时调用2 min 时刻SCADA 装置量测的节点注入功率数据(P2、Q2)以及2 min 时刻后μPMU装置量测的节点电压数据(U1、U2、U3…),使用本文提出的分段辨识方法对改变后的拓扑结构进行辨识,如图7 所示。
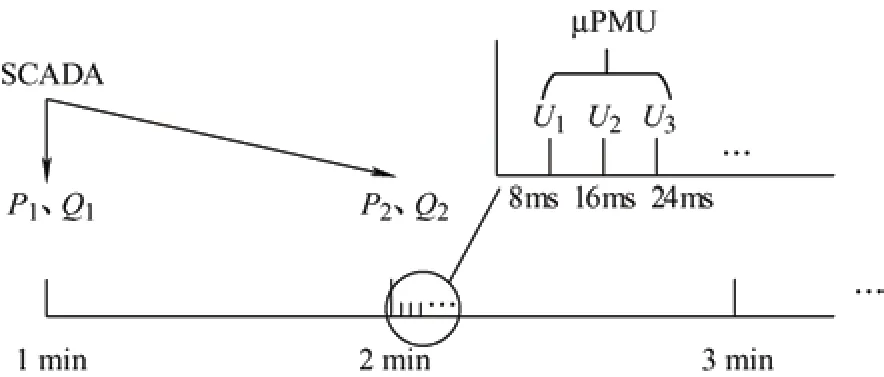
图7 SCADA、μPMU 装置的数据采样
为使辨识结果更为准确,可以使用拓扑变化后μPMU 装置1 s 内量测的多组数据{U1(8 ms)、U2(16 ms)、U3(24 ms)…}对拓扑结构进行多次辨识,取频次最高的拓扑识别结果作为真实的配电网拓扑结构。本文使用特定拓扑结构下潮流计算获得的节点注入功率和电压数据,模拟SCADA 系统和μPMU装置在量测误差为0 时的理想量测数据。
4.5 配电网拓扑分段辨识框架
分布式电源的接入改变了配电网的功率传输特性和节点电压幅值特性。本文提出拓扑结构辨识方法分两步进行。
第一步:采用“超节点”概念,对配电网拓扑结构变化进行识别,并确定拓扑改变部分。
第二步:根据DG 接入前后配电网电气特性变化特点,进行分段线路识别、末段线路识别和分段线路连接识别。具体识别流程如图8 所示。
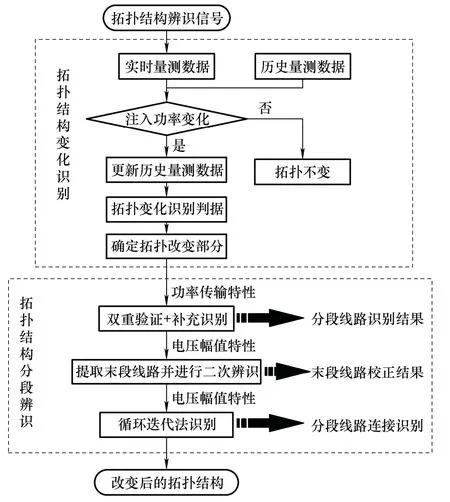
图8 配电网拓扑结构辨识
5 算例分析
本文在Matlab 环境下对所提方法进行仿真验证。使用IEEE-33 算例系统模拟实际中压配电网,以线路31-32 断开,联络线17-32 投入为例进行拓扑结构辨识验证,如图9 所示。

图9 IEEE-33 配电网系统
分布式电源配置如下:8、15 节点接入PV 型分布式电源,电压幅值的标幺值(p.u.)为1.0、1.02,有功功率注入(kW)为50、70;21、24、31 节点接入PQ 型分布式电源,有功功率注入(kW)为630、630、70,无功功率注入(kVar)为405、405、45。
5.1 拓扑改变识别
利用SCADA 系统获得功率量测数据,计算节点注入有功功率变化量,绘制图10。

图10 拓扑改变前后节点注入有功功率变化量
由图10 可知,与联络线17-32 形成环路的线路5-17、5-32 上节点注入功率变化显著,通过拓扑改变识别判据可以确定,配电网拓扑结构改变,且开关状态改变的支路位于线路5-17、5-32 和联络线17-32 形成的环路中,如图11 所示。
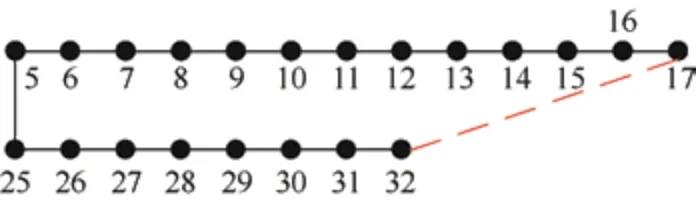
图11 拓扑结构改变部分
判据不仅能识别拓扑改变,还能识别改变的拓扑范围,降低了拓扑复杂度,缩短了辨识所需时间。
5.2 配电网拓扑结构分段辨识
本节按照分段线路识别、末段线路识别和分段线路连接识别的顺序进行拓扑结构分段辨识。
5.2.1 分段线路识别
通过SCADA 系统获得辨识出的拓扑改变部分的节点注入功率,将量测数据代入式(6)计算两两节点的有功、无功注入功率差值绝对值的和,采用第4.1 节提出的双重验证和补充识别的节点连接关系辨识方法,分别对无DG 接入和DG 接入两种情况下的配电网拓扑结构进行分段线路识别,识别结果如表1 所示。

表1 分段线路识别结果
从表1 可以看出,本文所提方法完成了对拓扑改变部分的节点连接关系的初步识别。分段线路识别方法基于配电网传输功率的递减特性提出,只是将变化拓扑中的节点连接关系部分识别出,并未辨识出节点间的所有连接关系,拓扑辨识结果呈现分段特性。从表1 的识别结果还可以看出,DG 接入带来的配电网功率传输变化致使分段线路识别结果发生改变,线路分段节点改变,DG 接入节点8、15成为分段点。
5.2.2 末段线路识别
由于不同线路的末节点注入功率相近,基于功率传输特性识别的分段线路中,末段线路的节点连接关系可能出现错误,故需要对包含末节点的末段线路进行二次辨识。
提取出分段线路中的末段线路(联络线节点和注入功率最小节点所在分段线路),通过μPMU 装置获得末段线路的节点电压量测数据,使用式(7)计算两两节点间的电压幅值差值绝对值,仍旧使用第4.1节提出的双重验证和补充识别方法对末段线路的节点连接关系进行识别,末段线路识别结果如表2所示。

表2 末段线路识别结果
以无DG 接入为例,将表1 中的分段线路⑤、表2 中的分段线路⑤、⑥的节点连接关系与图9 的真实拓扑结构分别进行对比。可以看出,分段线路识别结果中的末端线路的节点连接关系错误,经过二次辨识的末端线路中的节点连接关系正确,即末段线路的二次辨识纠正了分段线路识别结果的错误。综合表1、表2 的识别结果,将正确的分段线路识别结果列于表3。

表3 二次辨识后的分段线路识别结果
5.2.3 分段线路连接识别
第5.2.1 节和5.2.2 节完成了改变拓扑中节点间连接关系的部分识别,即完成了对改变拓扑中节点连接关系的分段辨识。为了获得完整的拓扑结构,需要对分段线路间的连接关系进行识别,即识别表3 中分段线路①、②、③、④、⑤、⑥、⑦间的连接关系。
提取识别出的分段线路端节点,通过μPMU 装置获得端节点的电压量测数据,根据式(8)计算两两节点间的电压幅值差值绝对值,使用第4.3 节提出的循环迭代法对分段线路的连接关系进行辨识,识别结果如表4 所示。将表4 的分段线路连接识别结果绘制于图12。

表4 分段线路连接识别结果
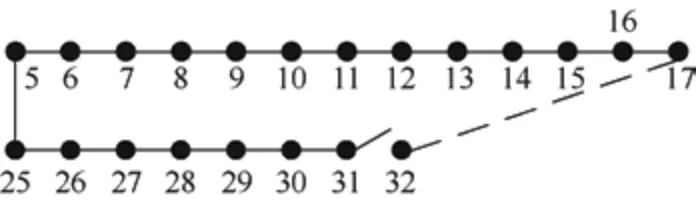
图12 有无DG 接入的配电网拓扑结构辨识结果
由表4 和图12 可知,对于无DG 接入和DG 接入的两种情况,本文所提方法均能正确、有效辨识配电网拓扑结构。
5.3 方法有效性对比
本文所提方法和文献[11]的电压偏差法、文献[23]的回路功率法都使用了功率量测数据辨识配电网拓扑结构。仍然使用IEEE-33 节点系统,以DG接入,线路28-29 断开,联络线17-32 投入为例,比较三种方法的有效性。DG 接入配置保持不变,识别结果如表5 所示。

表5 三种方法识别结果
配电网入口、各分支入口处的配电稳定性要求高、线路连接稳定,线路开关处于常闭状态。故对于IEEE-33 节点系统,仅考虑线路5-17、18-21、22-24、25-32 中的开关状态改变以及相应联络线7-20、8-14、11-21、17-32、24-28 的投切产生的多种拓扑结构。分别使用三种方法对多种拓扑结构进行识别,三种方法的辨识准确率如表6 所示。
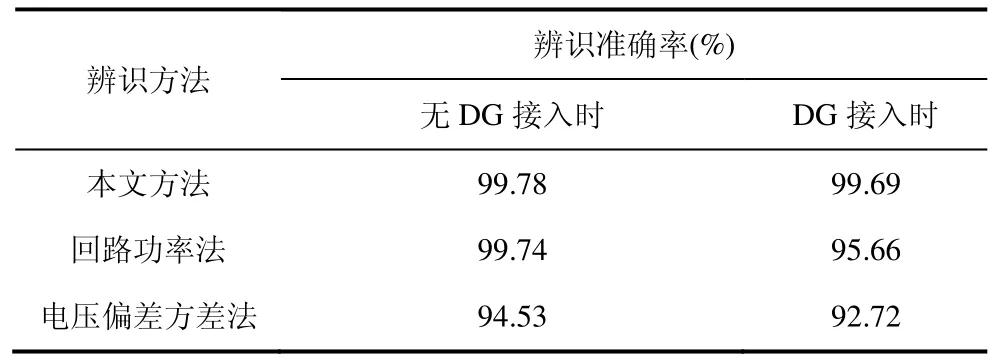
表6 三种方法的辨识准确率
从表5、表6 的识别结果可以看出,本文所提方法正确识别了改变后的拓扑结构,方法辨识准确率高。回路功率法面对DG 接入出现识别错误,这是因为当PV 型DG 接入时,拓扑结构变化导致的节点电压变化会使DG 向配网传输的无功功率发生变化,此时叠加线路损耗功率变化将使回路功率法辨识出现错误,所以回路功率法在DG 接入时,拓扑辨识的准确率明显降低。虽然拓扑变化前后节点注入功率因DG 接入有所改变,但本文方法基于DG接入前后配网功率传输特性的共性提出,所以依然能对DG 接入的配电网拓扑结构进行有效辨识,方法辨识准确率高。
电压偏差法虽然正确地识别了断开支路和联络线的投入,但对度数大于2 的节点5 和大负荷节点12 的连接关系识别错误。这是因为枢纽节点和大负荷节点与周围节点的注入功率相差较大,基于节点注入功率的电压偏差方差法难以识别它们的连接关系,故电压偏差法的辨识准确率不高。而DG 接入后,接入节点与周围节点的注入功率同样可能相差较大,故DG 接入后,电压偏差法的辨识准确率进一步下降。本文通过补充识别和分段线路连接识别解决了这一问题。
5.4 方法鲁棒性分析
由于噪声干扰,量测数据存在量测误差。为测试本文所提方法在量测误差存在时的有效性,需要对方法的鲁棒性进行分析。通过向潮流计算出的理想电压、功率数据μ中加入高斯白噪声e,模拟量测装置测量的配电网实际运行数据,高斯分布的标准差为
式中,σ为高斯分布标准差;μ为高斯分布均值。
本文设置四种噪声组合:①e1=0.2%,e2=5%;②e1=0.5%,e2=10%;③e1=1%,e2=15%;④e1=5%,e2=20%。其中e1为μPMU 装置量测误差,e2为SCADA 系统量测误差。前三组噪声组合在两种装置量测误差的正常范围内,第四种噪声组合考虑SCADA 系统与μPMU 装置测量时标没有对齐的极端情况。方法有效性如表7 所示。
从表7 结果可以看出,本文所提方法在正常的量测误差范围内均能有效识别配电网拓扑结构,方法鲁棒性好。
5.5 方法的适应性分析
为了验证拓扑辨识方法对于不同配电系统的适应性,使用IEEE-118 算例系统,以线路49-50 断开,联络线 46-54 投入为例进行方法适应性分析,IEEE-118 算例系统如图13 所示。

图13 IEEE-118 配电网系统
分布式电源配置如下:14、32、69、90、102节点接入PV 型分布式电源,电压幅值的标幺值(p.u.)为1.0、1.0、1.0、1.02、1.0,有功功率注入(kW)为50、50、50、70、50;17、62、118 节点接入PQ 型分布式电源,有功功率注入(kW)为530、530、70,无功功率注入(kVar)为305、305、45。
使用拓扑变化识别判据计算节点注入功率变化,图13 中虚线内的节点的注入功率发生变化。对虚线内的拓扑结构进行辨识,二次辨识后的分段线路识别结果和分段线路连接的识别结果如表8 和表9 所示。
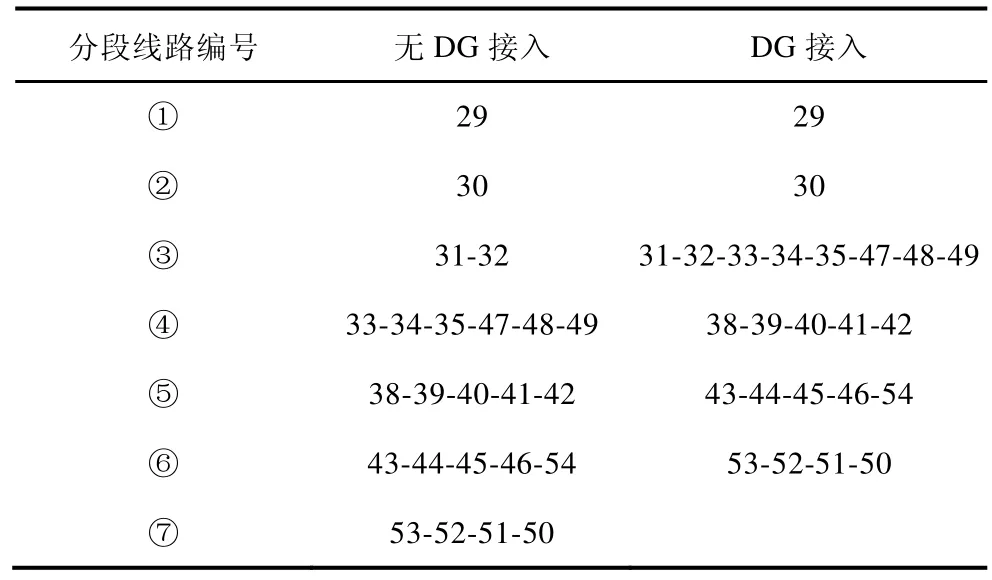
表8 二次辨识后的分段线路识别结果

表9 分段线路连接识别结果
将分段线路连接识别结果绘制于图14。

图14 拓扑结构辨识结果
由表9 和图14 可知,对于IEEE-118 的配电网大算例系统,本文所提方法依然能够正确、有效地进行拓扑结构辨识,方法适应性好。
6 结论
针对量测数据不足且大量分布式电源接入的配电网难以进行拓扑结构辨识的问题,本文提出了基于电气特性分析的拓扑结构分段辨识方法。得到的主要结论如下所述。
(1) 结合节点注入功率变化与“超节点”概念的拓扑变化识别方法,仅对拓扑改变部分进行识别,避免了对拓扑未改变部分的重复识别,缩小了拓扑辨识范围,提高了拓扑识别效率。
(2) 提出的拓扑改变分段辨识方法,仅需要分段线路端节点和末段线路节点的电压量测数据,在电压量测数据缺失的配电网中,仍能够有效进行拓扑结构辨识。
(3) 方法在分析分布式电源接入前后配电网电气特性的基础上提出,在分布式电源接入时,仍能有效识别配电网拓扑结构。
