一种高增益零输入电流纹波Sepic 变换器

郭 瑞 郭 佳 王国翰

(1.辽宁工程技术大学电气与控制工程学院 葫芦岛 125105；2.国网冀北电力有限公司承德供电公司 承德 067000)

1 引言

根据英国石油公司(British petroleum，BP)最新发表的2021 年《BP 世界能源统计年鉴》，由于2020年新冠疫情的爆发，全球可再生能源占比有所降低，碳排放量也创造历史新低，但可再生能源需求量仍然很大，其中风能和太阳能的需求量占比最重。据统计，在2020 年，太阳能发电量增幅20%，创造了新高，对可再生能源发展做出重要贡献。应用太阳能进行发电不仅在全球使用越来越广泛，其发电量在中国总发电量中的比重也越来越大。太阳能是一种对环境友好的可再生能源，是有效解决中国能源稀缺问题的重要途径，发展前景向好。我国能源主要消耗领域集中在电力行业，光伏发电量在电力行业比重很大。光伏发电系统中光伏组件输出电压等级较低，需要高增益直流变换器实现电压增益提升，因此学者们对高电压等级低器件应力等方面进行了广泛研究[1-2]。

传统变换器由于寄生参数影响，存在开关器件电压应力高、电压尖峰较大、输出增益小、效率低等缺点。对此，国内外学者提供了不同拓扑结构及控制方式来解决此类问题。

(1) 级联型[3-4]。通过变换器间级联方式来提升输出电压等级，但是存在拓扑结构不稳定，开关器件电压应力高、元器件数目多且不经济、效率低等问题。

(2) 开关电容型[5-6]。通过进行开关电容拓扑结构组合，实现高增益功能，电压应力降低，但电容在实现能量传递的同时存在较大的尖峰电流，不适用于功率较大的场合。

(3) 开关电感型[7-8]。基于开关电感单元提高电压增益，通过引入磁集成技术或交错并联技术来减小输入电流脉动，但电路结构复杂，变压器设计困难，成本高且增益提升有限。

(4) 耦合电感型[9-12]。引入耦合电感单元，改变耦合电感匝比来实现高增益功能，解决了开关器件电压应力高和因谐振产生的尖峰问题，具有结构简单、经济性好、损耗低、效率高的优点，因此得到广泛关注。

耦合电感的引入也导致输入电流纹波大的问题，降低了电池的使用寿命及转换效率。为消除输入电流纹波，文献[13]采用两个开关管，在固定的占空比时才能消除输入电流纹波，存在控制复杂、损耗大的问题；文献[14-15]采用两相或多相交错并联技术，但消除纹波必须在固定的占空比条件下，受到占空比限制；文献[16-17]采用耦合电感技术，在特定耦合系数下才能降低纹波，变压器设计复杂；文献[18-19]为电流馈入型变换器，利用较大输入电感消除纹波，导致变换器体积大，动态响应慢等问题；文献[20-21]提出的方案一定程度上降低了纹波，但拓扑结构复杂，成本较高。

本文在传统Sepic 变换器拓扑上，引入耦合倍压单元，前级并联一个无源零输入电流纹波电路，引入耦合电感倍压单元，在变换器高增益性能的同时，降低输入电流纹波脉动，实现零纹波，开关器件电压应力也得到降低。与上述文献相比，本文所提的倍压单元一方面易于叠加，另一方面电流纹波与占空比、漏感、励磁电感的数值无关，具有可靠性高、变压器参数设计简单等优点。

2 变换器电路拓扑以及工作原理

2.1 变换器拓扑的提出

本文提出的变换器拓扑结构如图1a 所示，其中包含一个MOSFET 开关管S，电容C1～C5和C0，二极管D1、D2、Do，负载电阻R0。为了便于分析，将励磁电感与理想变压器和漏感组成耦合电感倍压单元，等效电路如图1b 所示。耦合电感T1电压比为N1(n2:n1)，励磁电感为Lm1，漏感为LK1；耦合电感T2电压比为N2(n4:n3)，励磁电感为Lm2，漏感为LK2。为了便于理论分析，进行如下假设。

图1 电路拓扑及其等效电路

(1) 电容足够大，电容两端电压视为定值。

(2) 漏感与电容谐振周期很大。

(3) 除耦合电感的漏感外，各元器件均较为理想器件，耦合系数为K1=K2=Lm/(Lm+LK)。

2.2 基本工作原理

图2 为所提变换器工作在连续导通模态下，即CCM 模式下，变换器各个器件的电压电流波形。图3 为变换器模态回路，由于漏感的影响，在一个开关周期内变换器包括5 个工作模态。

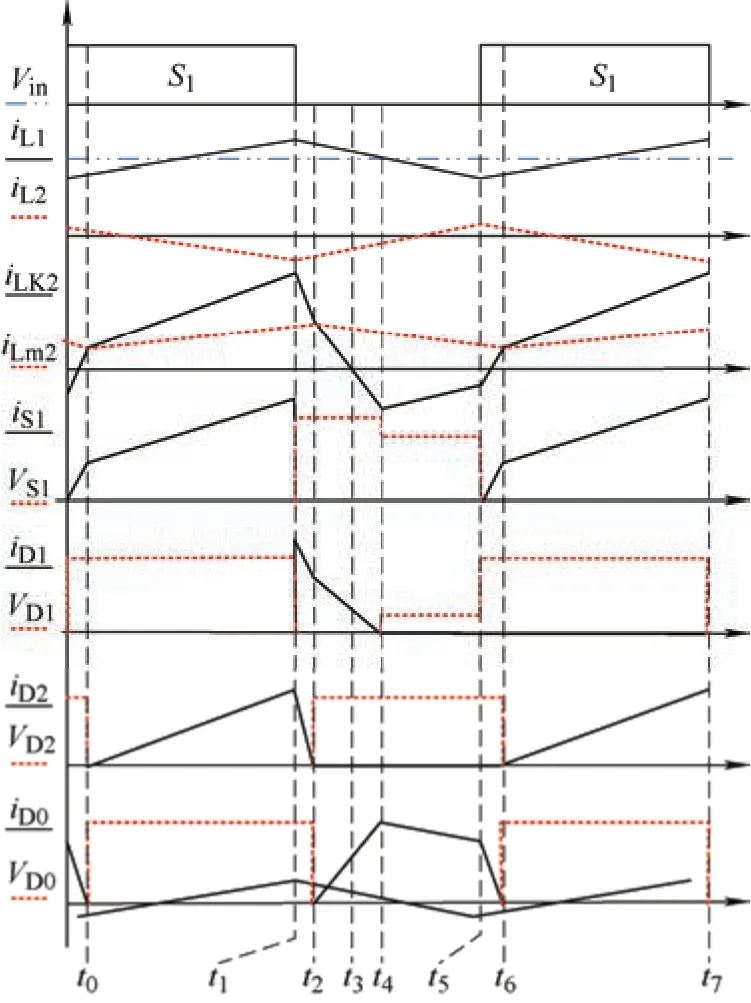
图2 变换器主要工作波形

图3 各开关模态的等效电路

开关模态Ⅰ[t0,t1]：在t0时刻，开关管S1和二极管D2正向导通，二极管D1和D0关断，输入电压Vin向输入电感提供能量，电感L1两端的压降升高为为输入电压Vin，电流iL1线性上升，输入电源与电容C3向变压器T2原边放电，励磁电感储能，漏感电流iLK2迅速上升，电流iL2、iLm1线性下降。

为保证变换器输入电流纹波为零，则在相同时间，电流iL1的上升斜率和电流iL2下降斜率的大小相等，消除电流纹波。

开关模态Ⅱ[t1,t2]：在t1时刻，开关管S1关断，二极管D1快速导通，D0反向截止。输入电源和储能电感L1为电容C5供电，变压器T2一次侧漏感经二极管D1向电容C5释放能量，漏感电流快速下降，变压器T2的二次侧继续为电容C4供电，电流iL1开始线性下降，而电流iL2开始线性上升，该模态持续时间很短。

开关模态III[t2,t4]：开关管S1持续关断，在t2时刻，二极管D2实现零电流关断，二极管D0由截止变为导通状态；t3时刻前，变压器T2原边释放能量，励磁电感电流线性减小，副边和电容C4经二极管D0向负载供电，漏感电流iLK2在t3时过零，在t3时刻后反向增大。

为保证变换器输入电流纹波为零，在相同时间，电流iL1的上升斜率和电流iL2下降斜率的大小相等，消除电流纹波。

开关模态IV[t4,t5]：在t4时刻，二极管D1关断，电感L1与上一模态相同，变压器T2励磁电感在输入电源、电感L1和电容C3作用下储能，漏感电流iLK2开始反向线性上升，电容C4能量经过二极管D0向负载释放，副边电流iS减小。开关S1导通时，此模态结束。

开关模态V[t5,t6]：在t5时刻，开关管S1实现零电流导通。励磁电感释放能量，副边电流iS减小，变压器T2电感副边为负载供能，t6时刻，漏感电流上升到和励磁电感电流相等时，二极管D0随之零电流关断，此模态结束。

3 性能分析

所提变换器正常工作时处于CCM 状态。设耦合电感系数为K=Lm/(Lm+LK)，为了便于稳态分析，只考虑持续时间较长的开关模态，故只考虑开关模态I、III、IV，根据电感伏秒平衡原理，可得

3.1 电压增益M

根据式(1)和式(9)，由电感1L的伏秒平衡可得

根据式(5)和式(11)，由电感Lm2的伏秒平衡可得

当变换器在开关模态Ⅰ时，根据拓扑结构可得

联立式(16)～(19)可得

根据开关模态III，得出输出电压Vo表达关系式为

联立式(20)～(23)，得出变换器在电流连续模式下电压增益为

当K2=1 时，变换器的增益为

由式(24)可知，变换器的电压增益不仅受占空比影响，还受匝比和耦合系数影响。可以通过调节变压器的匝数和耦合系数来实现高电压增益性能，避免出现极限占空比。

图4 是当耦合系数K2(K2=1)固定时，选取不同匝比N，电压增益G和占空比D的关系图。由图4可知，当占空比固定时，匝比越大，变换器输出电压增益越高。可以通过提高匝数降低占空比数值，避免极限占空比问题。

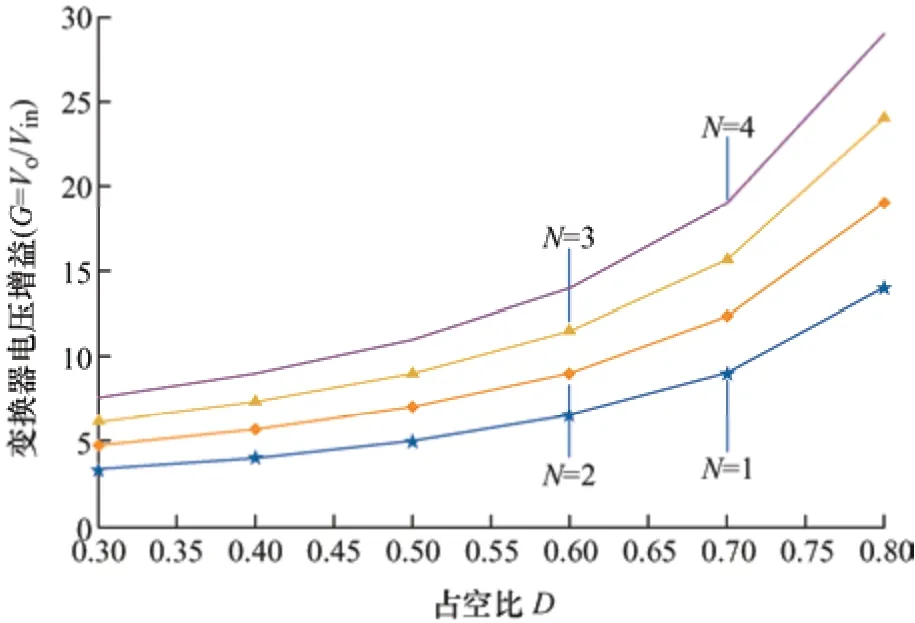
图4 不同匝数比N 的情况下占空比D 与电压增益G 的关系

图5 是变压器2T的耦合电感匝比N(N=2)固定时，所提变换器电压增益G的三维立体图，由图5 可知，变换器输出增益和耦合系数也正相关。

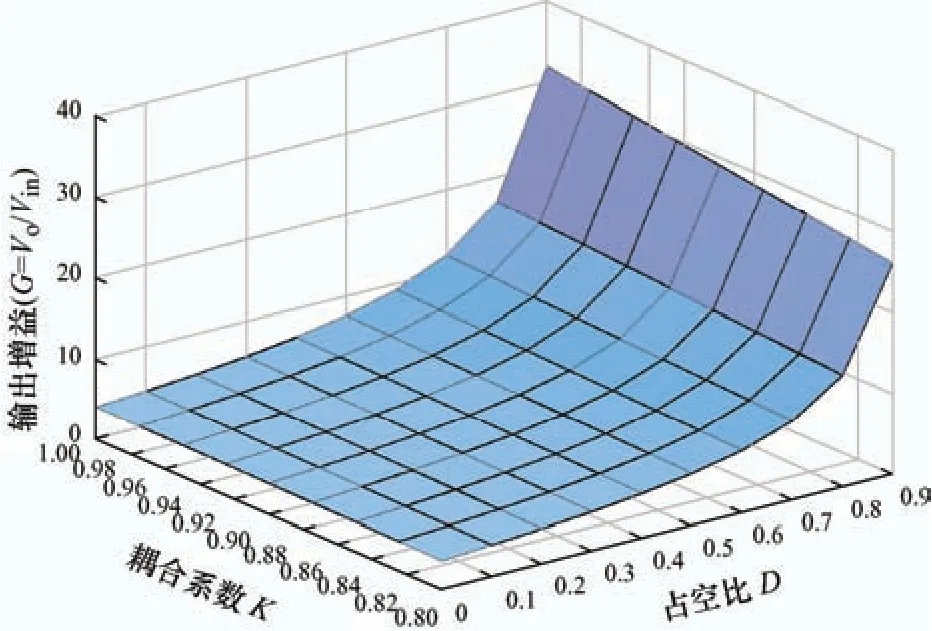
图5 变换器电压增益G 三维立体图

3.2 电压应力分析

为了简化分析，令耦合系数K2=1 ，根据第3.1节性能分析，开关S1和二极管1D的电压应力为

二极管D2和D0的电压应力为

由式(26)、式(27)可知，随着匝比N2的增加，开关管S1和二极管D1的电压应力随之降低，二极管D2和D0的电压应力随之增大，但所有器件电压应力均低于输出电压。

3.3 零输入电流纹波

为了便于进行零纹波条件分析，只考虑持续时间较长的开关模态，故只考虑开关模态I、III、IV，由式(6)和式(13)可得，变换器实现输入端电流纹波为零的条件表达式为

当匝比N1= 1时，漏感LK1远小于电感L2，故忽略不计，即LK1= 0，为进一步简化分析，令耦合电感T1的匝比N1= 1，式(28)简化为

3.4 DCM 工作模式

当变换器工作在断续模态，即DCM 模式。为便于分析，忽略过渡模态和漏感的影响，其主要工作波形如图6 所示。

图6 DCM 模式下工作波形图

变换器在DCM模式下和CCM模式下的分析方法相同，变换器匝数比为N，则电压方程表达式为

则输出电压表达式为

则DCM 模式下的电压增益为

根据图6 可知，励磁电感在开关S导通时线性增加，在导通时间内电流增加量等于最大值，则

式中，iLep为励磁电感电流和输入端电感电流之和，Le为等效电感，得

设D′T为励磁电感Lm从峰值降到最小值的时间，设D1T为二极管D1导通的时间，根据安秒平衡原理，得出二极管D1、D0电流最大值为

又设变换器的等效时间常数为τLe，则

式中，fs为开关频率。根据安秒平衡原理和式(33)～(36)得出DCM 模式下的电压增益为

当变换器处于临界状态模式，即BCM 模式下时，变换器的电压增益GCCM=GDCM，则可以得出电感时间常数表达关系式为

则通过仿真所得到的临界电感时间常数与匝比和占空比的关系如图7 所示，当变换器处于连续电流模式下即CCM 模式下时，τLe>τLeBCM；当变换器处于断续电流模式下即 DCM 模式下时，τLe<τLeBCM。

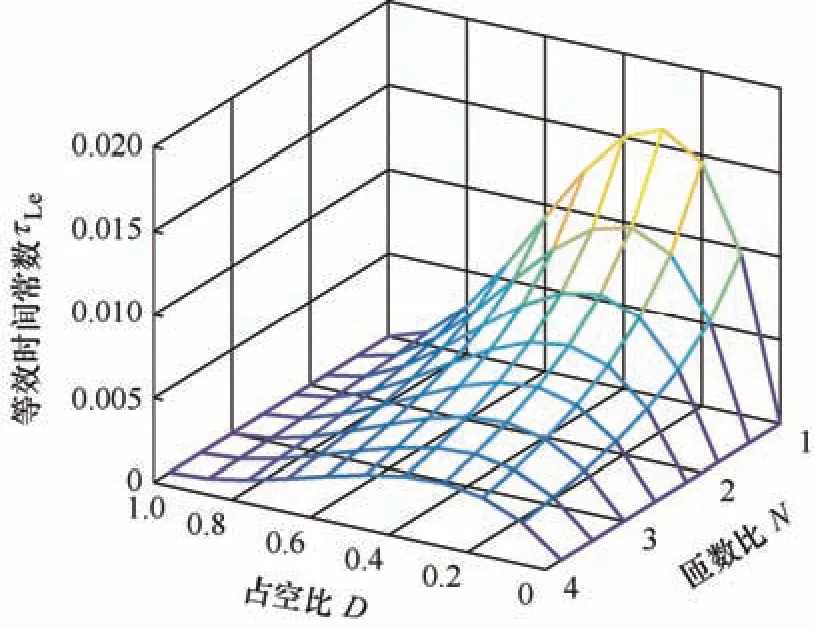
图7 临界电感时间常数与匝比N 和占空比D 的关系

4 开关电流应力

为了便于进行零纹波条件分析，只考虑时间较长的开关模态，故忽略时间较短的过渡模态，为实现输入电流纹波为零，变压器T1的匝比N1= 1，且电感L1=L2，图8 为在此情况下简化后的波形。

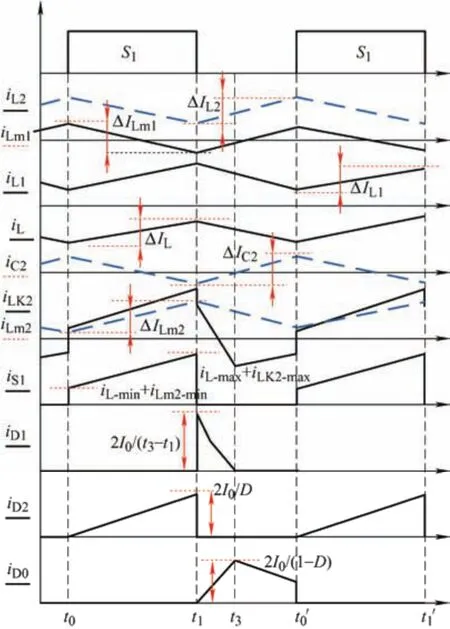
图8 简化后的主要工作波形

电感电流纹波值为ΔI，则可以推导出电路中电流表达关系式为

根据电感伏秒平衡原理，在一个开关周期内，励磁电流iLm2的平均值为零，输入电感电流IL的平均值与输入电流Iin的平均值二者相等。漏感电流和输入电感电流最大值表达式为

根据安秒平衡原理，可知二极管D1和D0的平均电流值等于输出电流值I0，则根据式(39)～(45)推断出二极管的电流应力最大值可表示为

不计变换器损耗，即设变换器输出效率为100%，由第3.2 节中式(27)可得输入电流表达关系为

开关管电流应力最大值在1t时刻取得，则开关管的电流应力表达关系式为

5 性能分析

5.1 性能对比

根据上述理论分析，将传统Sepic 变换器、文献[6]、文献[10]变换器和所提变换器之间的性能进行对比分析，汇总结果于表1。

表1 变换器之间的性能对比

图9 为不同变换器的输出增益与占空比关系曲线，图10 为不同变换器的开关管电压应力与占空比关系曲线。由图9 可知，本文所提出的零输入电流纹波Sepic 变换器和其他三个变换器相比输出电压增益最高。由图10 可知，本文所提变换器的开关电压应力与其他三个变换器相比最低。同时实现零输入电流纹波，变换器损耗降低，提升光伏组件中电池发电效率。

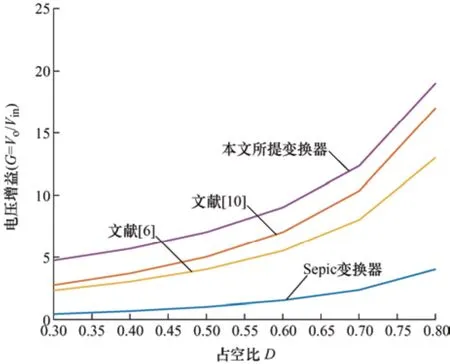
图9 不同变换器的电压增益与占空比的关系

图10 不同变换器的开关管电压应力对比

5.2 损耗分析

5.2.1 磁心损耗

变压器损耗主要由磁心产生，磁心损耗采用Steinmetz 经验公式(SE 公式)计算

式中，Pc为磁心损耗功率，f为变压器工作频率，Bm为磁感应强度峰值，Cm、α和β为损耗系数，一般由数据手册的数据曲线拟合得出。变压器的磁心一般为软磁材料，且磁心结构繁多，本文采用常用TDK 的“EE”型磁心，抗干扰效果好，应用广泛且散热好。

5.2.2 开关管损耗

通态损耗为开关管的主要损耗，根据进行式(26)的电压应力和式(50)的电流应力的分析，再根据开关管的选型，开关管的损耗为

式中，IDS(on)和RDS(on)分别为开关管的电流有效值和通态电阻，UDS为开关管的两端的压降。tr和tf分别为开关导通时间和截止时间。

6 试验结果与分析

为了验证理论分析的正确性，对所提出的变换器进行试验。在选择开关频率的时候，不宜选择开关频率过大，会损耗变换器，所以选择开关频率为50 kHz。图11 为搭建的100 W 试验平台，表2 为试验样机参数。

表2 试验样机的参数

图11 试验样机图

图12 为输入、输出电压试验波形图，在输入电压为12 V 的条件下，变换器实现输出电压100 V 的高增益效果；图13 为漏感电流iLK1和耦合电感原边漏感电流iLK2。图14 为二极管1D端电压VD1和开关管1S端电压VS1，二极管1D的两端压降接近于27 V，比输出压降100 V 小得多，由图14b 可知，开关管压降约为27 V，低于输出压降，且实现了零电流导通，二者电流波形与理论分析相同。

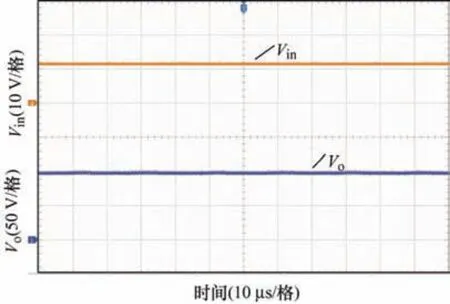
图12 Vin 、 oV 波形

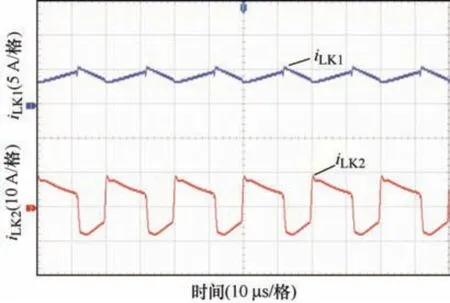
图13 iLK1 、 iLK2 波形

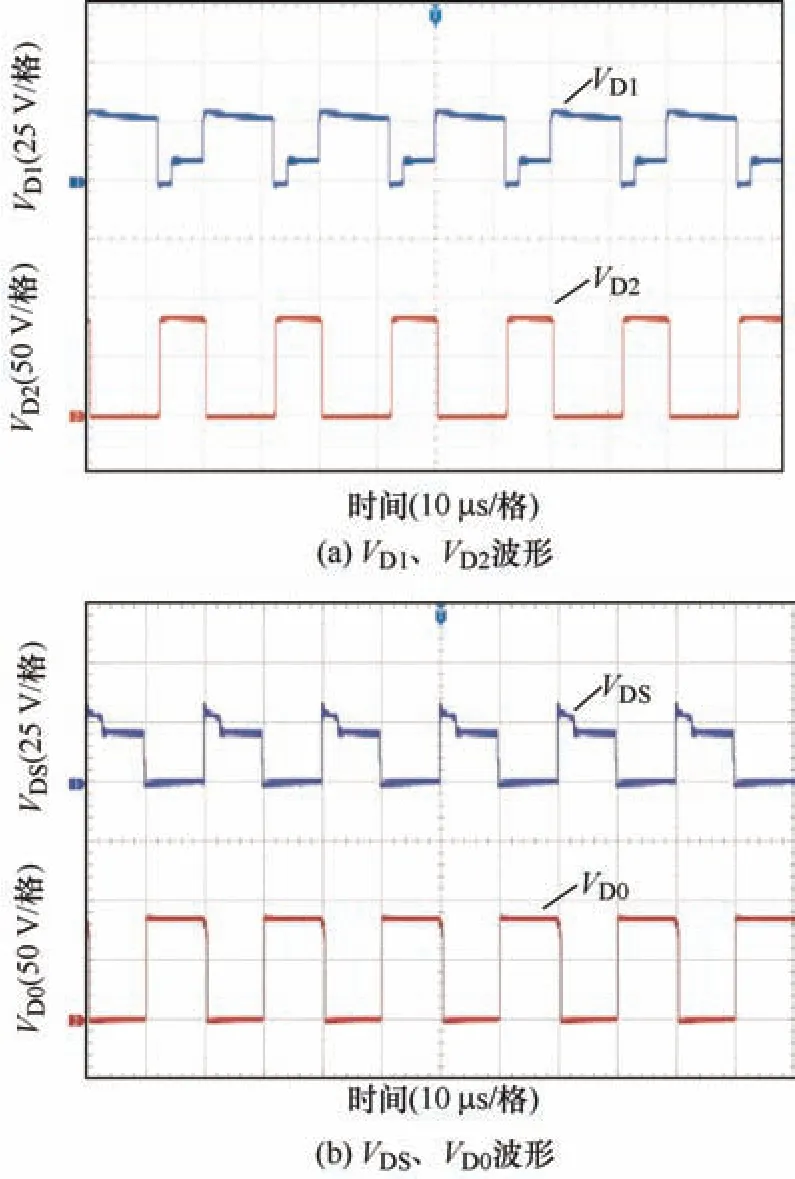
图14 开关器件电压波形图

各开关器件的电压应力如图14 所示。

图15 为开关器件的电流试验波形图，开关管实现零电流关断，由于实际电容有电压纹波，实际容值也具有一定误差，导致图16 所示的输入电流iin存在较小的脉动，近似实现零电流纹波。图16 为输入电流iin、电感1L电流iL1、电感2L电流iL2的试验波形图。

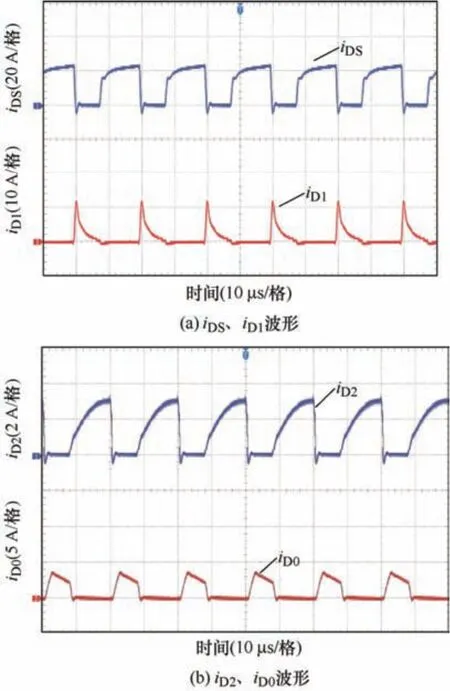
图15 开关器件电流波形图

图16 iin 、 iL1 、 iL2 波形

7 结论

本文提出一种零输入电流纹波的Sepic 变换器，详细分析了变换器在连续电流模式和断续电流模式下的工作原理及电流纹波等，并与其他变换器进行了性能对比分析。研究结果表明该变换器有以下特点。

(1) 拓扑结构只使用一个开关管，实现零电流导通效果，控制简单。

(2) 实现输入电流零纹波效果，该效果与占空比及耦合系数的数值大小无关，具有参数设计简单、可靠性高等特点。

(3) 由电容和二极管组成的钳位电路也能起到升压和吸收漏感能量的作用。通过选取合适的匝比即可提升电压增益，适用于各种需要高输出电压增益的场合。

(4) 倍压单元通过二极管与电容组合，具有叠加性，提高电压增益，避免极限占空比；由于变压器二次侧所在电路等效变压器一次侧的LC 电路，可以通过三次耦合方案减少器件使用。