三相矩阵式隔离整流器的最优调制比模型预测控制策略*
2024-01-15杨奕柏柳郭强
杨 奕 柏 柳 郭 强
(1.重庆理工大学电气与电子工程学院 重庆 400054;2.重庆理工大学重庆市能源互联网工程技术研究中心 重庆 400054)
1 引言
三相矩阵式隔离整流器(Three-phase matrix isolation rectifier,3MIR)由交流-交流矩阵式变换器衍生得到[1-3],具有输入电流正弦、功率因数可调、四象限运行、能量双向流动、功率密度高、系统可靠性高、无大容量储能元件等优点[4-6];且在引入高频变压器后,减轻了重量体积、增大了电压调节范围,同时还实现了电源端与负载端的电气隔离。因此,3MIR 在多电飞机系统、数据中心配电系统以及电动汽车充电系统等领域具有广阔的应用前景[7-10]。3MIR 的研究目前正处于初始阶段,存在调制方法复杂、控制策略难度大等问题,为了提高3MIR 系统整体性能,需要对其控制结合调制进行优化。
现阶段3MIR 常沿用交流-交流矩阵式变换器成熟调制策略。文献[11]采用基于输入侧电压的双电压调制策略,实现变换器能量的双向流动,该策略具有较好的鲁棒性,但其网侧功率因数不可调。文献[12]中利用开关函数算法验证了矩阵整流器的四象限运行能力,但其存在算法复杂、计算量大等问题。相较于前两种调制策略,双极性电流空间矢量调制(Bipolar current space vector modulation,B-C-SVM)因算法简单、直流利用率高、功率因数可调等优点[13-15],成为国内外学者的研究热点。
为实现3MIR 输出电压恒定、输入电流正弦化,文献[16]在闭环控制策略基础上,引入虚拟直流母线电压反馈环节,改善了网侧低频谐波污染,实现单位功率因数;文献[17]采用双直流环的控制策略实现对网侧电流的间接控制,此策略结构简单,易于工程实现;文献[18]提出一种含有源阻尼环路的双闭环控制策略,抑制了网侧LC 谐振,实现对网侧电流的跟踪;但是,上述双闭环控制策略存在PI参数整定较复杂、系统动态响应速度慢等缺点。
近年来,模型预测控制(Model predictive control,MPC)[19]作为一种最优化控制方法,被广泛应用在电力电子变换领域。传统MPC 策略是在离散化系统模型下,针对控制目标构建评价函数,再将开关状态组代入评价函数,以便下一周期选择出使评价函数最小值化的最优开关状态组合。与双闭环PI 控制策略相比,传统MPC 策略控制概念简单,且无需PI 参数整定、系统动态响应迅速。文献[20]利用MPC 策略代替传统电流控制内环,减少繁琐的PI 参数整定,实现网侧电流快速跟踪参考值;文献[21]在MPC 的基础上,引入多模型自适应算法,通过滚动优化找到预测模型的最优系统参数;文献[22]针对无储能电容导致的弱抗扰性,提出在开关表序列分配环节引入偏磁控制,从而改善系统动态性能。然而,上述MPC 策略均以开关表滚动寻优作为核心控制思想,存在系统运算量大、开关频率不固定等不足,且其输出开关状态具有随机性,会使3MIR 原边电压波形正负不对称,从而导致高频变压器饱和无法正常工作。
因此,本文以3MIR 为研究对象,首先,分析了应用于3MIR 前级电路的B-C-SVM 调制策略,对B-C-SVM 下3MIR 的输入、输出表达式进行推导;其次,为减小网侧电流畸变率、维持输出电压恒定、加快系统动态响应速度,对传统MPC 策略进行优化,提出一种基于最优调制比的模型预测电流控制策略,利用评价函数求导出最小电流误差对应的最优调制比,并结合B-C-SVM 策略产生最优开关状态组合来等效滚动寻优环节,在实现系统固定开关频率、减少运算量的同时,保证了每个PWM 周期内的原边电压波形正负对称,提高了系统稳定性;最后,将本文所提模型预测控制策略与传统双闭环PI 控制、传统模型预测控制进行仿真对比。
2 拓扑结构及调制策略
2.1 3MIR 的拓扑结构及工作原理
如图1 所示,3MIR 拓扑结构由前级三相-单相矩阵电路、中间高频变压器、后级二极管全桥整流电路以及输入输出LC 滤波器组成。其中,usa、usb、usc为网侧电压;isa、isb、isc为网侧电流;uta、utb、utc为前级三相-单相矩阵电路的输入电压;ita、itb、itc为前级三相-单相矩阵电路的输入电流;up、ip、us、is分别为高频变压器原边和副边的电压、电流;Uo、Io分别为输出电压、电流。
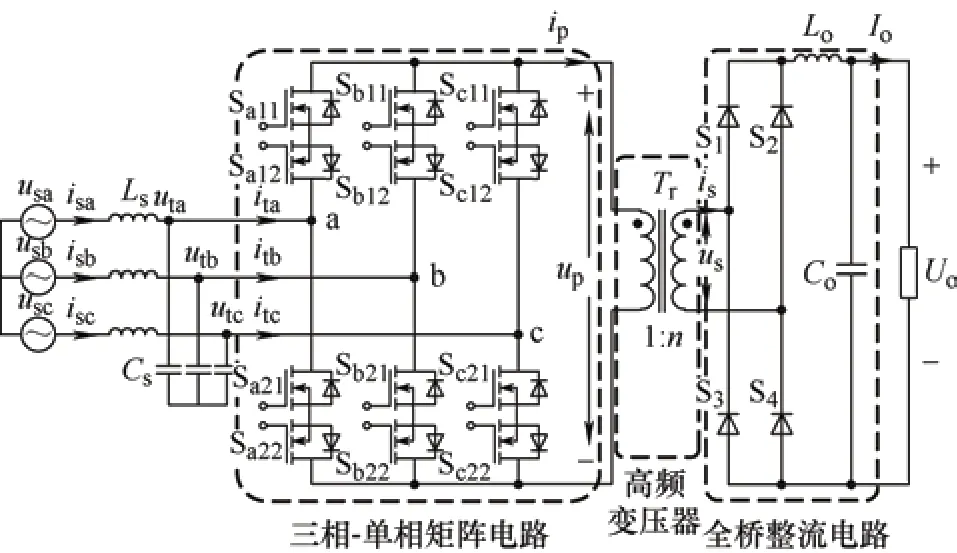
图1 三相矩阵式隔离整流器拓扑结构
前级三相-单相矩阵电路由六个双向开关管构成,实现由三相工频交流源到单相高频交流源的变换,中间环节无需储能元件;其中,双向开关管由两个独立的SiC-MOSFET 反串联组成实现四象限运行;中间高频变压器Tr(1∶n)将原边能量传输至副边,再经过后级全桥整流和滤波电路获得所需输出电压。
2.2 3MIR 的调制策略
3MIR 前级电路在每个工作周期内相当于两个正负极性相反的传统电流源型PWM 整流器交替工作。因此,基于常规空间矢量调制策略,衍生出双极性电流空间矢量调制,从而获得正负交变的高频脉冲信号。
如图2 所示,在一个工作周期中,B-C-SVM 的输入电流空间矢量Iref前半周期为,由所在扇区左右相邻的有效电流矢量Ix+、Iy+和零矢量合成;后半周期为,由与Ix+、Iy+极性相反的两个有效电流矢量Ix-、Iy-和零矢量合成得到。

图2 输入电流空间矢量合成
式中,Ts为开关周期时间;Ty+、Tx+、T0+、Ty-、Tx-、T0-分别为矢量Iy+、Ix+、I0+、Iy-、Ix-、I0-的导通作用时间,其中,Tx+=Tx-,Ty+=Ty-,T0+=T0-。
图2 中各矢量作用的占空比可根据正弦定理得到,分别为
式中,Tx=Tx++Tx-,Ty=Ty++Ty-,T0=T0++T0-;调制比m=Im/nIo(0≤m≤1);ϕ为输入电流空间矢量与有效矢量之间的夹角,ϕ=(ωt-θ)+π/6。
前半周期和后半周期的输入电流平均值可通过各矢量占空比和输出电流表示为
将式(2)代入式(3),得到周期内的输入电流表达式为
式中,ω为网侧电压基波角频率;θ为输入电压与电流相位差;Im为输入电流幅值。
由式(4)可知当Im不变时,输入电流仅与θ有关,即θ是输入功率因数的控制变量。为实现单位功率因数运行,令式(4)中θ=0,可得到
由于3MIR 前级电路输出与高频变压器相连,需要输出正负交变的高频脉冲电压来维持高频变压器伏秒平衡。因此,本文提出工作周期对半均分,正负电压交替输出的调制思想。
如图3 所示为基于图2 对应的原边电压up分布波形,可知前半周期输出正极性电压Uab、Uac和零电压,后半周期输出负极性电压Uba、Uca和零电压,每半个周期按照输出电压绝对值“先高后低”的序列导通,从而实现每个工作周期内输出电压平均值为0。根据伏秒平衡原理有
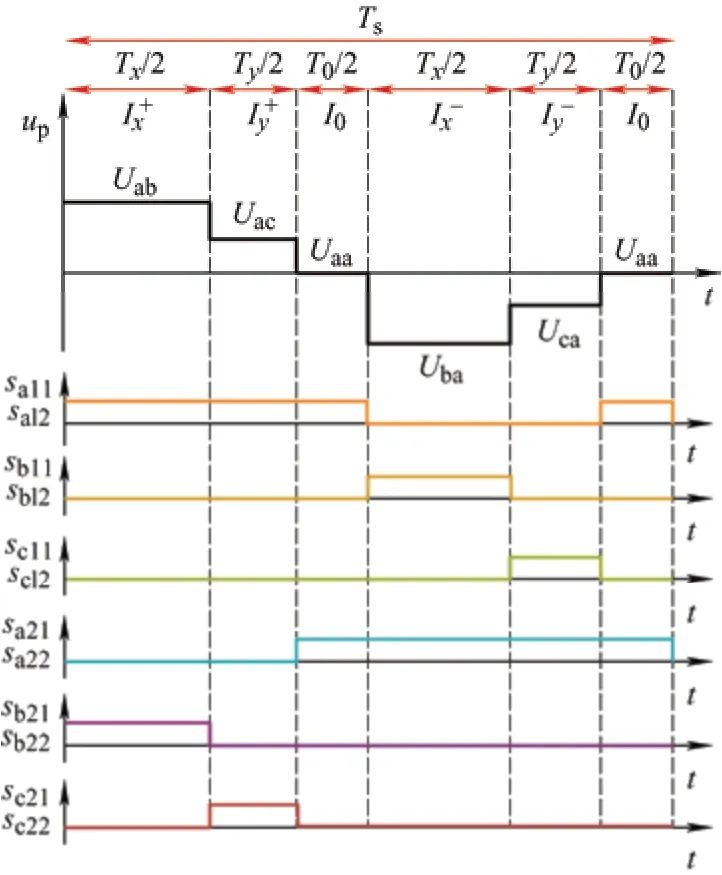
图3 一个工作周期的原边电压分布
将ϕ=(ωt-θ)+π/6(其中θ=0)和式(2)代入式(6),得
式中,Um为输入电压幅值。
由式(5)、式(8)可知,当θ=0 时,能实现单位功率因数运行;并且当Um和高频变压器变比n不变时,输出电压Uo大小仅与调制比m有关,即控制m能够改变输出电压Uo大小。
3 模型预测电流控制策略
在3MIR 拓扑中存在9 种开关状态、9 种有效电流矢量,导致传统MPC 开关表滚动寻优环节过程复杂,且系统开关频率不固定;针对上述不足,本文基于传统MPC 控制策略,结合B-C-SVM 调制所需调制比m,提出一种改进型模型预测控制策略,从而减小系统运算量、固定开关频率、实现网侧电流正弦化以及直流输出电压恒定。
如图4 所示为本文所提控制策略框图,整个系统由内外两个控制环组成。外环采用PI 控制器维持直流电压恒定,以及输出内环电流参考值,为实现单位功率因数,将q轴电流参考值设为0,再通过反Park 变换获得α、β轴下的内环电流参考值内环采用模型预测控制,将检测到的网侧三相电压usj(j=a,b,c)、电流isj(j=a,b,c)和输入滤波电容电压utj(j=a,b,c)变换到αβ坐标系下,通过3MIR 离散化数学模型计算出网侧电流预测值isα(k+1)、isβ(k+1),并 将 此 预 测 值 延 时 补 偿 得 到isα(k+2)、isβ(k+2),再与直流外环输出的网侧电流参考值构成评价函数,最后为实现最小网侧电流误差值的控制目标,对评价函数求导从而获得极值点对应的最优调制比m,结合B-C-SVM 调制产生脉冲信号驱动双向开关管,实现网侧电流的快速跟踪。

图4 3MIR 模型预测电流控制策略框图
3.1 3MIR 的数学模型
根据图1 和基尔霍夫定理可得,3MIR 交流侧的状态方程式为
式中,Ls、Cs分别为网侧滤波电感、电容值;r为网侧滤波电感与线路的寄生电阻。
式(9)通过Clarke 变换可表示为
式中,usα、usβ分别为α、β轴下的网侧电压;isα、isβ分别为α、β轴下的网侧电流;utα、utβ分别为α、β轴下的输入电压;itα、itβ分别为α、β轴下的输入电流。
调制比m在α、β轴下可定义为
式中,mα、mβ为调制比m在α、β轴的分量。
3.2 电流预测值
将式(10)代入式(11),得到αβ坐标系下的网侧电流表达式为
采用一阶前向欧拉法对式(13)进行离散化,其中采样周期为Ts。由于网侧内阻值较小,可忽略r;且网侧电压周期远大于采样周期Ts,则有最后得到式(13)离散后的表达式为
由式(14)可得k+1 时刻的网侧电流表达式为
3.3 延时补偿
在模型预测电流控制的每个采样周期内都需要重新预测网侧电流值,由于采样时间、信号处理时间、响应时间等多种因素会导致计算时间较长,最终使得调制信号作用存在延时。为了消除差拍延迟引入提前预测法,将k+2 时刻的网侧电流预测值进行控制,从而实现无差拍补偿。k+2 时刻网侧电流值可表示为
对式(10)和式(12)离散化,忽略寄生电阻r,分别得到k+1 时刻网侧电流、输入电流关系式
为消除式(16)中k+1 时刻的网侧电流值和输入电流值,将式(17)、(18)代入式(16),得到k+2 时刻的网侧电流表达式为
3.4 评价函数的构建
在传统MPC 策略中,评价函数是用于寻找每个采样周期中最优开关组合,从而使控制目标误差最小化。因此,常选用简单易算的差值形式来表示。本文为了减小传统MPC 繁琐的运算量,利用求解最优调制比m使评价函数值最小化来替代开关表滚动寻优环节,为得到最优调制比m,评价函数采用可导的方差形式来表示。
由于本文控制目标是实现网侧电流实际值与参考值的误差最小化,再考虑到αβ坐标系下电流变化和延时问题对控制的影响,评价函数可表示为
式中,isα(k+2)、isβ(k+2)分别为k+2 时刻的网侧电流预测值;分别为网侧电流参考值;λ为权重系数。
3.5 电流调制函数求解
由式(19)可看出评价函数中的网侧电流预测值是关于调制比m的函数式。因此,在每个采样周期内找到最优调制比m来使评价函数最小值化,是本文所提模型预测电流控制算法的核心思想。为了使电流误差最小值化,本文通过对评价函数中的调制比m求导,从而找到极小值点对应的最优调制比m。
联立式(19)~(21),其中权重系数λ可消除,分别得到αβ坐标系下极值点对应的调制函数mα(k+1)、mβ(k+1)关系式为
最后通过公式m=得到k+1 时刻下的最优调制比m,并结合B-C-SVM 技术产生调制波驱动功率开关,从而实现网侧电流的跟踪。
4 仿真与验证
为验证本文所提控制策略的可行性与有效性,利用Matlab/Simulink 软件搭建3MIR 仿真模型,在相同参数运行下,将本文所提改进型模型预测控制与传统双闭环PI 控制、传统模型预测控制进行对比研究,系统仿真参数如表1 所示。其中,传统双闭环PI 控制利用Matlab/SISO 设计工具,通过配置控制器零点位置与增益大小,实现对内、外环PI 控制器的设计,然后再反复调试内、外环PI 控制器,最终使系统处于最优状态。

表1 3MIR 系统参数
图5 为3MIR 高频变压器原边电压up的波形。可看出传统模型预测控制策略的原边电压波形呈现不规则状态,在每10 μs 中原边电压由多个随机的有效矢量组成,开关频率不固定,且系统运算量较大;而在本文所提控制策略中,每个PWM 周期内的输出波形仅由4 个有效矢量以及零矢量正负交替组成,保证输出相连的高频变压器伏秒平衡的同时,还实现开关频率的固定以及系统运算量的降低,验证了本文所提控制策略的高效性。
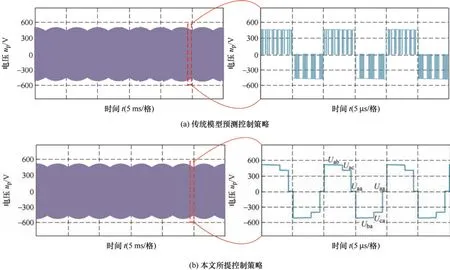
图5 原边电压仿真波形
在相同运行条件下,三种控制策略的a 相网侧电流波形及其谐波含量分析如图6 所示。通过图6 可知三种控制策略下的网侧电流均实现正弦化,且与网侧电压同相位。但是通过FFT 分析可看出传统双闭环PI 控制下的网侧电流总谐波畸变率THD 为1.47%,传统模型预测控制的网侧电流THD 为1.08%,而本文所提控制策略下网侧电流THD 仅为0.92%,网侧电流谐波含量远小于前两种控制策略,验证了本文所提控制策略的有效性。
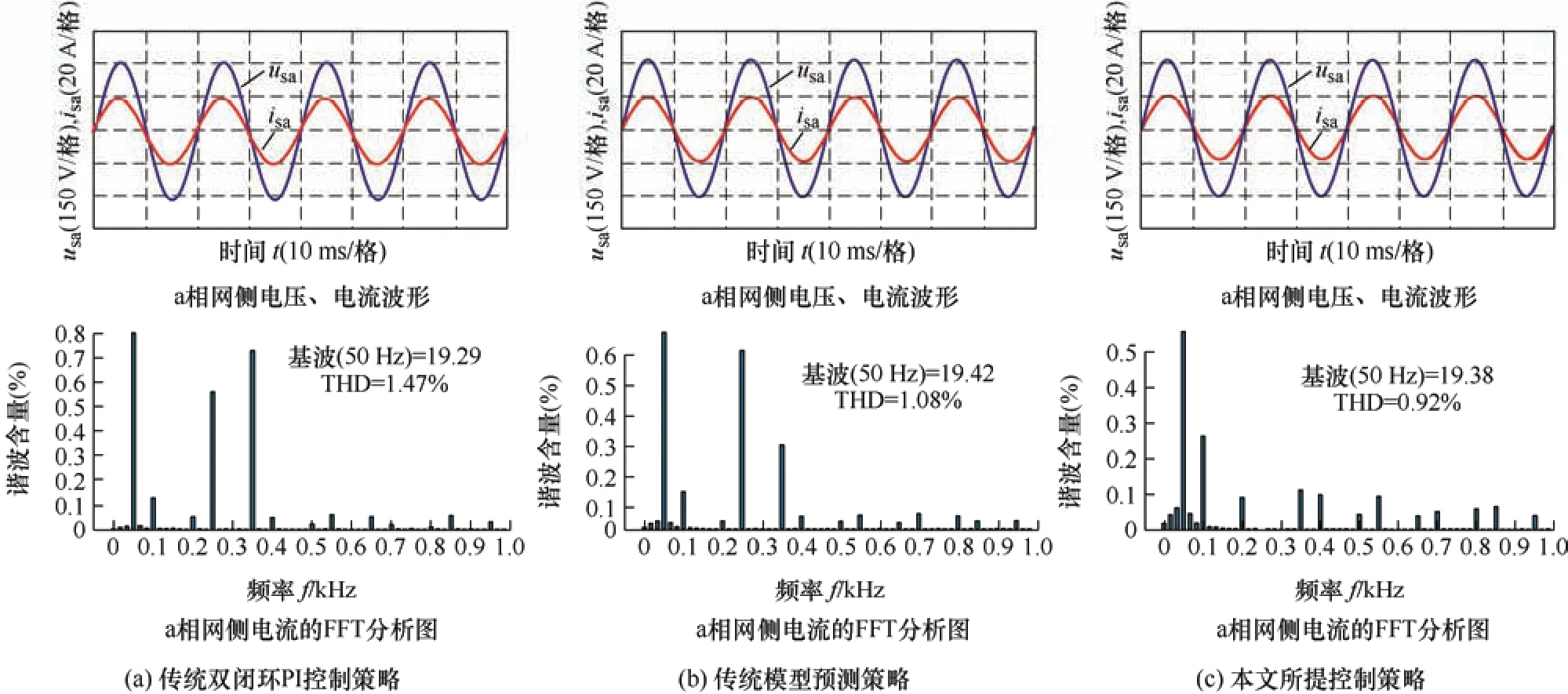
图6 网侧电流仿真波形以及FFT 分析图
图7 为三种控制策略下有功功率、无功功率以及输出电压、电流的仿真波形。当输出稳定后,传统双闭环PI 控制下有功功率稳态误差达到350 W,功率纹波4.4%,无功功率在±220 Var 间波动;传统模型预测控制下有功功率稳态误差为280 W,功率纹波3.5%,无功功率在±170 Var 间波动;相较前两种控制策略,本文所提控制策略下有功功率稳态误差仅100 W,功率纹波1.25%,且无功功率波动范围为±120 Var,减小了稳态功率波动,实现高功率因数运行。通过三种控制策略下的输出电压、电流波形可以看出:在输出稳定后,三种控制策略的输出电压和电流均能达到给定值,跟踪效果较好;传统双闭环PI 控制输出电压、电流纹波分别为2 V、0.15 A,传统模型预测控制输出电压、电流纹波分别为2 V、0.2 A,而本文所提模型预测电流控制的输出电压、电流纹波分别为1 V、0.04 A,减小了输出稳态误差,证明了本文所提控制策略具有更好的静态性能。
为讨论三种控制策略的动态性能,在0.04 s时刻将负载从20 Ω突变到10 Ω,三者的仿真波形如图8 所示。可看出双闭环PI 控制在负载突变时出现 130 V 的输出电压跌落,需要经过0.015 s 才能回到电压给定值;而传统模型预测控制策略和本文所提控制策略输出电压跌落仅为75 V 左右,且在0.01 s 内能够恢复到稳态给定值,具有较好的动态响应性能。负载突变时,三种控制策略的网侧电流始终与网侧电压同相位;但相较双闭环PI 控制,传统模型预测控制策略和本文所提控制策略下的网侧电流畸变率更小、动态响应速度更快,验证了本文所提控制策略在改进传统模型预测控制的同时,仍保留了其良好的动态性能。
为验证本文所提控制策略良好的动态性能,将纯阻性负载替换成感性负载,其中电阻值R=20 Ω,串联电感值LR=20 mH,并在0.04 s 时刻将电阻值R从20 Ω突变到10 Ω,其仿真波形如图9 所示。由图9 可见,感性负载突变时,输出电压、电流需要经过0.015 s 恢复到稳态给定值;相较纯阻性负载,感性负载突变时输出电流上升曲线平滑、无振荡纹波,且输出电压跌落仅为50 V,网侧电流畸变率更小。
通过前文对传统双闭环PI 控制、传统模型预测控制以及本文所提控制策略的仿真研究,归纳得出三种控制策略的特性对比结果,如表2 所示。

表2 三种控制策略特性对比
5 结论
本文以3MIR 为研究对象,对传统MPC 策略进行优化,提出了一种基于最优调制比的模型预测电流控制策略;利用评价函数求导出最小电流误差对应的最优调制比,并结合B-C-SVM 调制共同实现对3MIR 的控制。通过仿真分析,可以得出如下结论。
(1) 本文所提控制策略在保留传统MPC寻优环节的同时,实现了开关频率固定、系统运算量减小。
(2) 相比传统双闭环PI 控制,本文所提控制策略不仅实现了网侧电流正弦化、输出电压恒定,同时保留了传统MPC 策略参数整定简单、网侧电流谐波含量低、有功无功波动范围窄、直流输出纹波小、动态响应速度快的优点。
