基于光谱-空间注意力残差网络的高光谱图像分类

汪菲菲，赵慧洁，李娜，李思远，蔡昱

（1 北京航空航天大学 仪器科学与光电工程学院 精密光机电一体化技术教育部重点实验室，北京 100191）

（2 北京航空航天大学 人工智能研究院，北京 100191）

（3 北京航空航天大学 “空天光学-微波一体化精准智能感知”工信部重点实验室，北京 100191）

（4 中国科学院西安光学精密机械研究所 光谱成像技术重点实验室，西安 710119）

（5 中国运载火箭技术研究院，北京 100076）

0 引言

高光谱图像（Hyper Spectral Image，HSI）通过几十甚至上百个光谱通道来提供丰富的光谱信息，可用于对各地物类别进行准确分类［1］。高光谱图像分类是高光谱影像处理和应用领域的一个热点研究方向，分类模型通过分析每个像素的光谱信息与空间信息，对该像素所属类别进行预测，然后与实际地物进行对应比较，实现地物目标分类。深度学习由于其强大的特征学习能力成为高光谱分类的主流算法。

在基于深度学习的分类算法，根据是否提取到数据的空间信息，可分为基于光谱和基于光谱-空间融合的分类方法。基于卷积神经网络（Convolutional Neural Networks，CNN）的方法是一种带有卷积结构的前馈神经网络［2］，是一类非常重要的高光谱地物分类方法。其中基于光谱的分类方法使用一维卷积操作提取到待分类像素的光谱信息进行分类。HU Wei 等［3］利用一维卷积神经网络提取像素光谱信息来进行分类。MOU Lichao 等［4］利用循环神经网络来进行高光谱图像分类，其本质上也是利用了一维卷积网络进行分类。基于光谱的方法虽然简单，但是其精度无法令人满意。高光谱的空间上下文信息也有助于提高分类精度，因此现在常见分类算法都是基于光谱-空间信息融合的。ZHONG Zilong 等［5］提出了一种光谱-空间变换网络，由光谱特征提取模块和空间注意力模块组成，充分利用HSI 的光谱-空间信息进行分类。而GHADERIZADEH S 等［6］则是提出利用混合三维和二维卷积神经网络来进行高光谱分类，其中三维卷积有效地提取光谱-空间信息，并用二维卷积来增强空间信息。WU Hao 等［7］将卷积神经网络和循环神经网络相结合提出了卷积循环神经网络，利用卷积操作提取到高光谱图像的光谱-空间信息，然后利用循环神经网络进一步提取光谱-空间特征上下文信息。ZHONG Zilong 等［8］提出了光谱空间残差网络，连续提取光谱信息和空间信息特征。SHI Yuetian 等［9］提出了利用多角度平行特征编码的方式，通过增强局部空间特征的方式提高图像分类精度，并且该算法对图像旋转鲁棒。与此同时，在高光谱图像实际分类任务中存在光谱相似、类别易混等问题，注意力机制广泛应用于分类任务，XU Yue 等［10］在三维光谱卷积模块中利用注意力机制进行光谱-空间特征选择和提取。YANG Kai 等［11］提出了交叉注意力机制，该网络分为像素和图像块2 个分支输入，并对像素分支网络采用光谱注意力机制提取光谱特征，并将该特征作用到图像块分支网络中。ZHENG Xiangtao 等［12］提出了中心光谱注意力机制，将中心光谱像素值作为特征权重对光谱特征进行新的校正，但高光谱图像块不可避免地包含干扰像素，因此采用全局平均池化引入干扰像素类别对注意力权重的生成不利。FANG Shuai 等［13］的研究表明了不同地物类别其分类所依靠的光谱波段并不相同，也说明不同类别的光谱冗余波段可能不同。为此，中心池化的操作可将中心像素值直接代替原有的全局平均池化后的像素，并根据该中心像素值生成光谱注意力权重。

尽管上述工作取得了不错的效果，但是还有如下问题：1）多数工作在使用光谱注意力机制后，直接进行了空间特征提取，没有单独提取光谱特征，或者是单独提取光谱特征时，默认光谱各维度同等重要；2）光谱注意力机制多采用全局特征或中心像素特征进行权重调整，前者引入了较多干扰像素；而后者忽略了周围相同类别对其的影响。

为了解决上述问题，本文提出了光谱-空间注意力残差网络（Spectral-Spatial Attention Residual Network，SSARN）来进行高光谱分类。该网络主要包括光谱特征学习、空间特征学习和分类器。其中，光谱特征学习部分包括光谱注意力模块和光谱残差网络模块；而空间特征学习部分包括空间注意力模块和空间残差网络模块。由于现有的光谱注意力模块通常采用全局平均池化或者中心池化来提取光谱特征，但是无论哪种方式都会丢失光谱特征，为此提出了一种新的光谱注意力机制，尽可能减少光谱信息损失。

1 光谱-空间注意力残差网络

高光谱图像是一个包含光谱信息和空间信息的三维立方体，基于此提出了一个用于高光谱图像分类的光谱-空间注意力残差网络（SSARN）。如图1 所示，SSARN 包括光谱特征学习、空间特征学习和分类器。其中，光谱特征学习部分包括光谱注意力模块和光谱残差网络模块；而空间特征学习部分包括空间注意力模块和空间残差网络模块。

首先高光谱图像会根据设定好的尺寸分割成图像块，然后这些图像块会被送入到网络中，根据各个模块提取图像特征，最后将特征输入到分类器中得到最终的分类结果。

1.1 中心区域光谱和空间注意力机制

1.1.1 中心区域光谱注意力机制

注意力机制的提出是为了节省资源，不需要让网络处理全部的输入信息，而是从这些信息中有选择地对与任务相关的信息进行计算［14］。根据处理任务时注意力机制作用的数据域位置不同，可分为光谱注意力机制和空间注意力机制。

光谱注意力机制在图像的光谱维度进行特征提取，也被称为通道注意力机制。图2 所示就是一种光谱注意力机制。由于高光谱图像包含几十甚至上百个光谱波段，而将全部波段放入网络中提取特征是不可行的，一方面需要大量的计算资源，另一方面这些波段和波段具有冗余关系［14］，可以用部分波段表征全部波段。主流方式用注意力模块重新调整各个波段的权重。该模块可以根据任务需要独立嵌入到任何网络中，自适应地生成注意力权重，即

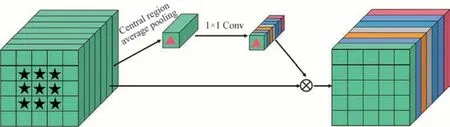
图2 中心区域光谱注意力机制结构Fig.2 The structure of the central region spectral attention mechanism

式中，权重参数η表示生成的每个波段的权重，fSpeA(⋅)表示光谱注意力，X表示高光谱图像块，σ(⋅)表示激活函数，FC(⋅)表示全连接层，ave(⋅)表示全局平均池化。权重越大的波段在后续特征学习时更容易得到神经网络的关注，提取更多的有利于高光谱分类的信息。通常，利用全局平均池化融合图像块的全部空间信息，然后对该信息利用全连接层和sigmoid 函数来自适应地生成权重η参数。不同地物类别其分类所依靠的光谱波段不相同［14］，中心池化操作是将中心像素值直接代替原有的全局平均池化后的像素，并根据该中心像素值生成光谱注意力权重［11］。虽然该方法在一定程度上避免了干扰像素对权重的影响，但是也丢失了周围相同类别的光谱特征对中心像素光谱权重增强的作用。

根据地理学第一定律［15］空间自相关性，待分类像素周围的像素可能属于同一类地物，因此周围的高光谱像素有可能会包含可用于提高分类结果的空间信息。所以一般在高光谱图像块中，周围像素与中心像素完全不同的概率较小，更多的是周围像素中包含了和中心像素相同的地物类别，并且越接近中心像素的区域，其包含相同类别的像素越多。为此，在现有的光谱注意力机制上提出了中心区域光谱注意力模块，在尽可能避免周围不同类别像素对中心像素干扰的同时，尽可能多利用周围相同类别像素波段对中心像素增强的作用。所提出的中心区域光谱注意力机制可以表示为

式中，Center3×3(X)表示中心区域3×3 范围的像素，conv(⋅)表示卷积和激活函数的操作，⊗表示卷积计算。如图2 所示，选取中心区域像素，对这些像素求取平均值，获得中心区域像素平均值。然后采用1×1 卷积和激活函数从基于中心区域平均像素生成注意力权重η。紧接着，利用该权重η与原始的图像块X 进行卷积获得经过光谱注意力机制的高光谱图像块。

1.1.2 空间注意力机制

空间注意力机制和光谱注意力机制的目的类似，都是将注意力转移到重要的部分，本质上是定位网络感兴趣的信息，抑制无用的信息。对于高光谱分类来说，空间包含的所有像素对中心像素的贡献并不是同等重要，只有能够帮助中心像素增加类间差异、缩小类内差异的像素才是网络需要关心的。空间注意力机制可以表示为

式中，δ代表空间注意力权重，[⋅]代表特征拼接，fm，fa分别代表最大池化和平均池化，X代表图像块（输入端）或者是空间-光谱特征（在网络中），代表经过空间注意力机制后的空间特征。空间注意力机制如图3 所示，将高光谱图像块X，经过池化层分别获取平均池化和最大池化特征，这两个特征在光谱维拼接后进行特征提取，输出经过注意力机制后的权重，最后和原始输入的空间特征进行卷积得到空间注意力机制后的空间特征。

图3 空间注意力机制结构Fig.3 The structure of the spatial attention mechanism

1.2 光谱和空间残差网络模块

在深度学习中，神经网络层数的增加引发梯度下降，网络会发生退化现象，即训练集的损失会逐渐增大，浅层网络的精度反而优于深层网络，失去了深度学习的优势。其原因在于随着网络层数的递增，提取的特征所包含的图像信息越来越少，导致网络的分类精度下降。残差网络可进行图像识别任务［16-19］，被广泛用于高光谱图像分类中［8，20-21］，其由一系列残差单元组成，标准的残差单元可以表示为

式中，xl+1代表第l+1层特征，F(xl，Wl，bl)代表对第l层特征进行特征提取，(Wl，bl)分别代表第l层网络参数，目的是让第l层和第l+1层的特征图保持大小一致，然后在输入输出前后增加一个恒等映射的跳跃连接，残差块的基本结构如图4 所示。

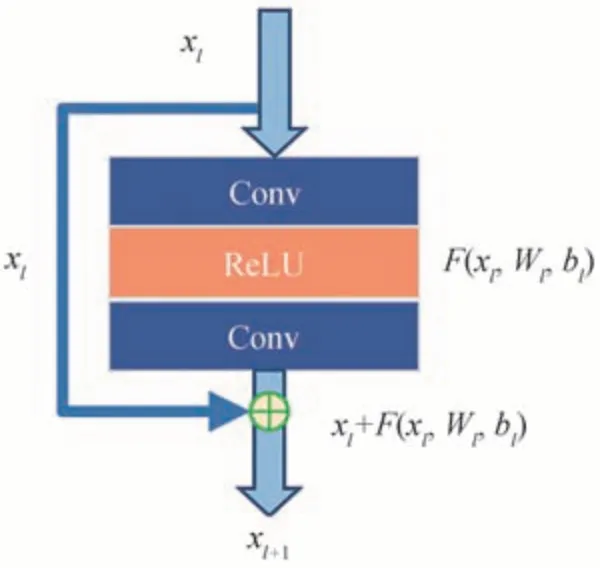
图4 残差块的基本结构Fig.4 The structure of the residual network

光谱特征学习的残差块如图5 所示，残差块包括两个连续的卷积层和一个跳跃连接，跳跃连接可以保证第p+2 层特征中包含有第p层的特征。对于第p层和第p+1 层，分别使用尺寸为1×1×m的卷积核Cp+1和Cp+2，并利用填充策略保持第p+1 层和第p+2 层的特征空间大小尺寸一致不变，即空间大小为w×w。最后，利用残差函数对第p层和第p+2 层进行连接。光谱残差网络模块结构可以表示为

图5 光谱残差网络模块Fig.5 The spectral residual network module

式中，Xp代表第p层的特征，F(⋅)代表特征提取的函数，r={Wp+1，Wp+2，dp+1，dp+2}代表第p+1 层和第p+2 层卷积核和偏置参数的集合，C代表卷积核参数，d代表偏置参数。

空间残差网络模块如图6 所示，残差块包括两个连续的卷积层和一个跳跃连接，跳跃连接可以保证第q+2 层特征中包含有第q层的特征。对于第q层和第q+1 层，分别使用尺寸为a×a×b的卷积核Kq+1和Kq+2，这些空间卷积核的光谱维度为b，等于输入特征图的光谱维度。利用填充策略保持第q+1 层和第q+2 层的特征空间大小尺寸一致不变，即空间大小为w×w。最后，利用残差函数对第q层和第q+2 层进行连接。因此，空间残差网络模块可以表示为

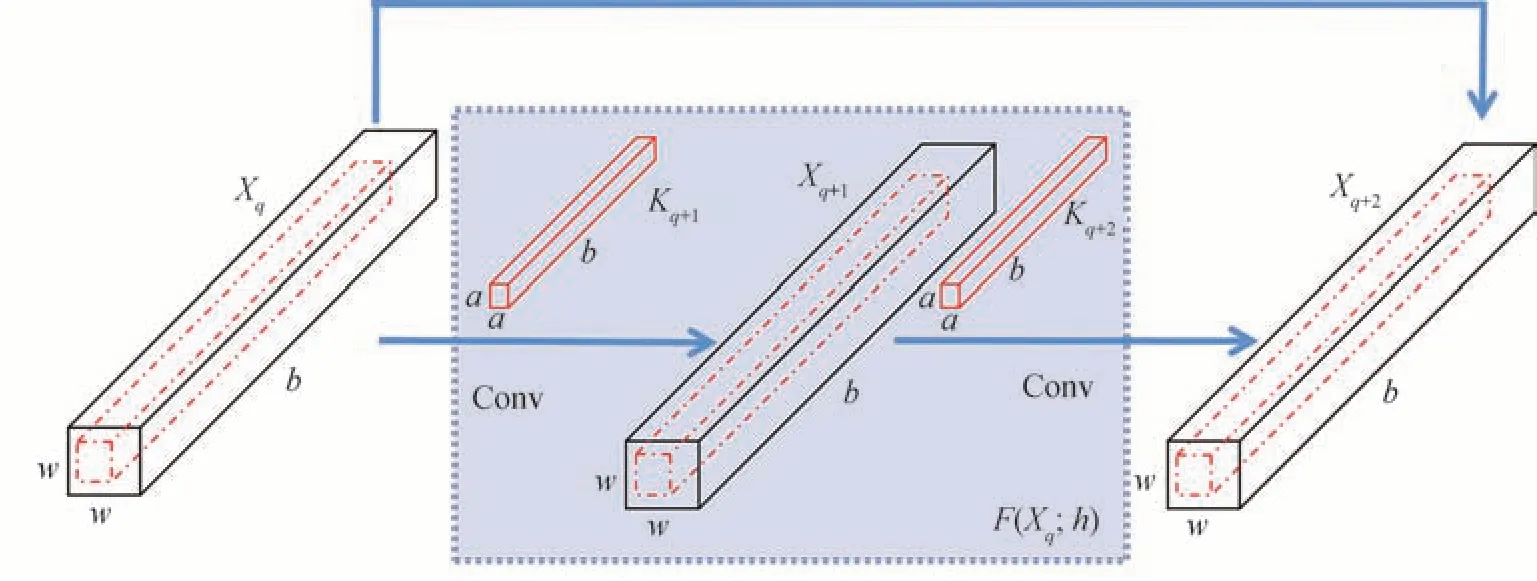
图6 空间残差网络模块Fig.6 The spatial residual network module

式中，Xq代表第q层的特征，F(⋅)代表特征提取的函数，h={Kq+1，Kq+2，lq+1，lq+2}代表第q+1 层和第q+2 层的卷积核和偏置参数，K代表卷积核参数，l代表偏置参数。

1.3 光谱-空间注意力残差网络

在上述内容基础上，提出了一个可以连续提取光谱和空间特征的高光谱分类网络，即图7 所示的光谱-空间注意力残差网络（SSARN），该网络包括光谱特征学习模块、空间特征学习模块和分类器。其中，光谱特征学习模块包括光谱注意力和光谱残差网络；而空间特征学习模块包括空间注意力和空间残差网络。并且在网络中每个模块之间添加跳跃连接，将分层特征的表示层连接成为连续的残差块，以缓解精度下降的现象。

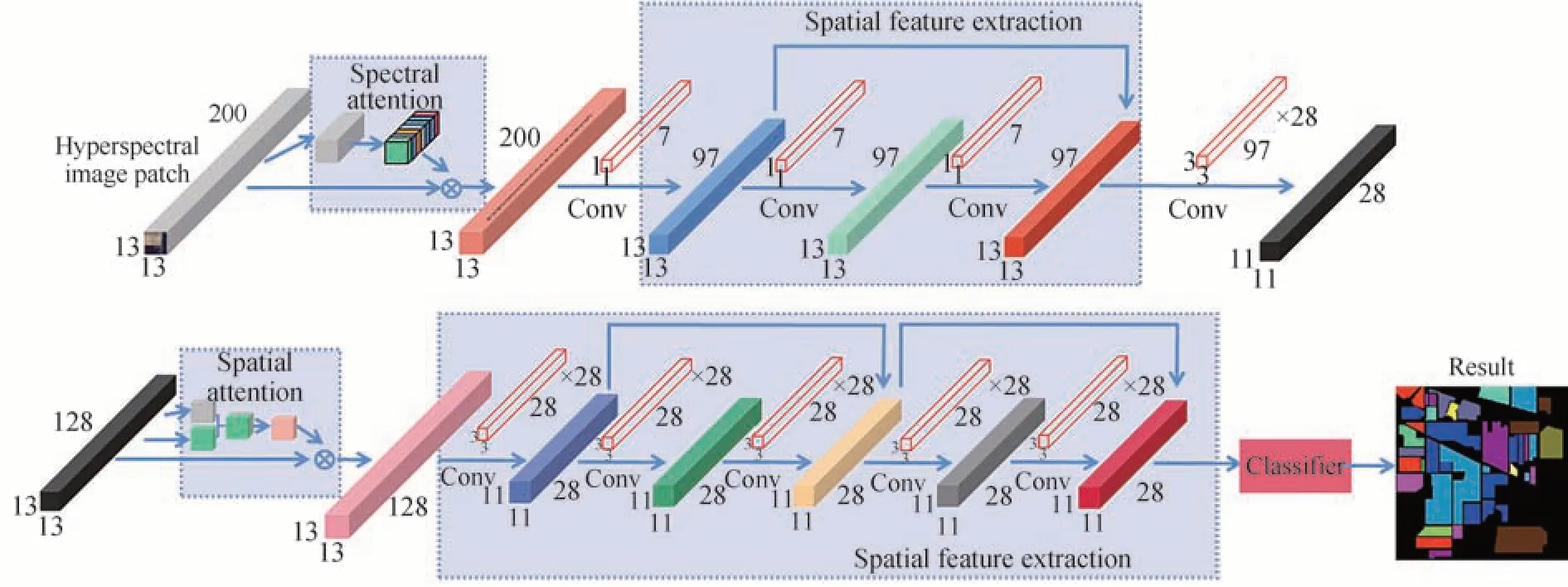
图7 以IP 数据集为例的SSARN 流程Fig.7 The flow chart of SSARN with IP dataset as an example

以Indian Pines （IP）数据集为例来解释所提出的SSARN 网络。首先，将高光谱图像逐像素分割为一定尺寸的图像块，为方便说明，假定图像块尺寸大小为13×13，其光谱维度为200。该图像块经过中心区域光谱注意力后，光谱波段权重被重新调整，提高重要波段权重，降低不重要波段的权重。经过该注意力模块后，其图像块尺寸依然为13×13×200。中心区域选取范围为以中心像素为基准，周围3×3 范围内为中心区域，一方面该范围内包含了一定相同类别的光谱信息，另一方面也尽可能减少不同类别像素的干扰。中心区域光谱注意力的计算方式如图2 和式（3）～（5）所示。

光谱特征提取部分包括1 个卷积层和1 个光谱残差网络。在HSI 中采用尺寸为1×1×n的三维卷积核提取光谱信息，不影响空间结构，保持了空间相关性。使用1×1×7 的三维卷积作为光谱卷积核。该卷积核对经过中心区域光谱注意力机制的特征进行卷积，卷积步长为（1，1，2）。经过卷积层后，生成了13×13×97的光谱-空间特征。随后，该图像块被送入到光谱残差网络中提取光谱特征。光谱残差网络模块包含2 个卷积层。在每个卷积层使用1×1×7 的光谱卷积核来学习光谱特征。为了能够使用残差连接，需要保证输入和输出同样的尺寸，因此需要在卷积层中使用填充来保持相同的尺寸，填充尺寸统一为（0，0，3）。图像块经过光谱注意力和光谱残差网络模块后，网络已经提取到相应的光谱特征，该特征尺寸为13×13×97，最后该特征输入到空间特征学习模块中。

空间特征学习模块包括1 个空间注意力和2 个空间残差网络模块。经过光谱特征学习后的空间-光谱特征输入到空间注意力模块中，进行空间权重重新校正，提高对中心像素的判别能力。空间注意力机制并不会改变特征的空间尺寸，因此经过空间注意力机制后的特征尺寸依然为13×13×97。接着使用28 个13×13×97 的三维卷积核提取空间-光谱特征，同时降低空间尺寸和光谱尺寸；输出的光谱-空间特征为11×11×28。在空间残差网络模块使用连续的二维卷积核提取空间判别特征，每层卷积均采用28 个3×3的二维卷积核，同时为了保证残差网络模块前后尺寸统一，需要使用空间填充，填充尺寸为（1，1）。经过4 个卷积层，2 个空间残差网络的特征学习，所提出的特征已经包含了丰富的光谱特征和空间特征。

将该特征放进分类器中，完成最后的分类任务。分类器包含平均池化层和全连接层，平均池化将提取11×11×28 的光谱空间特征变成1 个1×1×28 的特征向量。接着全连接层根据每个数据集所包含的类别数生成一个输出向量，并选取最大值为预测结果。

2 实验结果

2.1 实验设置

本次实验选取的数据为三组公开的Indian Pines（ IP）数据集、Salinas（ SA）数据集、Pavia University（PU）和Houston 2013 标准划分数据集。各个数据集的假彩色图和真值图如图8～11 所示。

图8 IP 数据集Fig.8 IP dataset

图10 PU 数据集Fig.10 PU dataset

图11 Houston 数据集Fig.11 Houston dataset

IP 数据集每类随机选择20%的样本作为训练样本，SA 数据集每类随机选择2%的样本作为训练样本，PU 数据集每类随机选择1%的样本作为训练样本。随机按照比例选取样本，可以保留数据集本身的样本不均衡问题，有效验证算法在面对样本分布不均衡的性能。Houston 数据集有标准划分，因此按照标准划分进行训练和测试。各个数据集的训练样本和测试样本见表1～4。

表1 IP 数据集的训练样本数量和测试样本数量Table 1 The number of training and testing samples on IP dataset

表2 SA 数据集的训练样本数量和测试样本数量Table 2 The number of training and testing samples on SA dataset

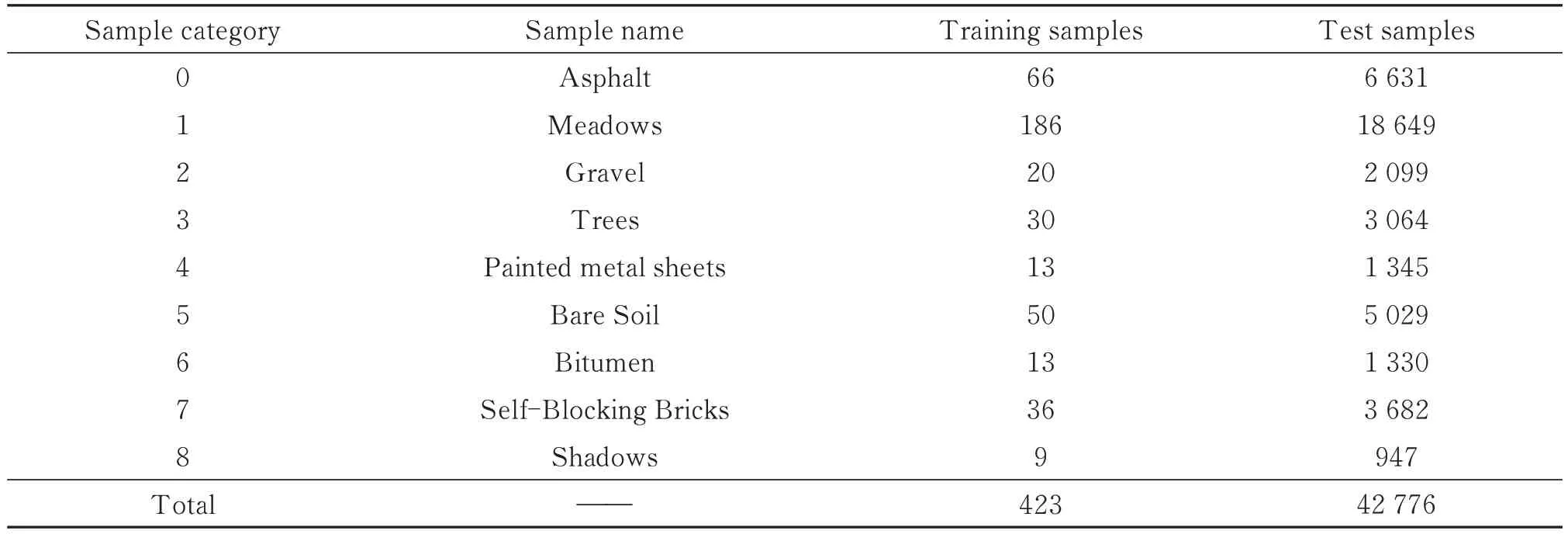
表3 PU 数据集的训练样本数量和测试样本数量Table 3 The number of training and testing samples on PU dataset

表4 Houston 数据集的训练样本数量和测试样本数量Table 4 The number of training and testing samples on Houston dataset

实验平台为Pytorch 1.12，Python 3.9 和Nvidia GTX 3090，24GB 图形处理器。所有算法的训练轮数设置为100，每次训练输入64 个图像块。损失函数、优化器都按照对比算法的最佳效果进行设置。所提出的光谱-空间注意力残差网络采用交叉熵损失函数，优化器为Adam 优化器。初始学习率为0.001，每10 轮学习率调整为原来的0.6 倍。

评价指标为总体准确度（Overall Accuracy，OA）、平均准确度（Average Accuracy，AA）和Kappa 系数。总体准确度（OA）表示正确分类的样本数占总样本数的比例，其公式为

式中，nij代表图像中第i类样本预测标签为j的样本数目，nii代表i类样本中分类正确的样本数目，Ni=∑jnij代表第i类样本待分类样本的数目。

平均准确度（AA）表示每一类分类精度的平均值，其公式为

式中，k代表待分类样本的类别。

Kappa 系数是用来衡量分类结果与真值地物之间一致性的指标。由于样本类别不均衡，OA、AA 的指标会受到大样本精度影响。Kappa 系数可以表示整个分类情况的偏差，代表分类与完全随机分类产生错误减少的比例，其公式为

2.2 图像块尺寸

图像块尺寸选取过大，则需要较多的计算资源和时间成本。而图像块尺寸过小，又有可能使得网络不能够充分学习图像的空间特征，导致分类精度较低。因此，详细探索不同的图像块尺寸对总体分类准确度的影响。其分类结果见表5。

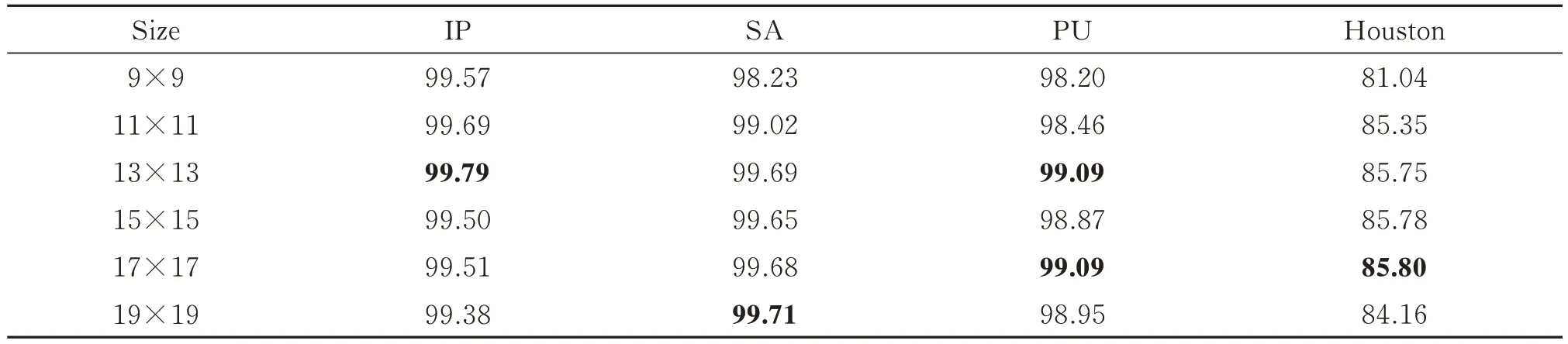
表5 不同图像块尺寸在四个数据集上的总体准确度Table 5 The overall accuracy of the different size of the patch on the four datasets

通过表5 可知，总体准确度总体上是根据尺寸大小先上升后下降。在IP 数据集上，13×13 的图像块精度最高；在SA 数据集上，19×19 的图像块精度最高，在较小尺寸的图像块上精度都有所下降。在PU 数据集上，13×13 和17×17 的图像块精度一样，但在19×19 时开始下降。在Houston 数据集上，随着尺寸的增加，其精度不断提高，在17×17 时达到最高精度。

对于IP 数据集，其样本区域较为平滑，不同样本区域之间有交错但边缘区分较为明显，因此随着图像块尺寸的增大，其包含的空间信息越丰富，分类准确度也有所上升；当图像块尺寸超过一定尺寸时，有可能包含了更多的冗余空间信息，例如不属于同一类别的样本空间信息，反而会使分类精度下降。对于SA 数据集，其样本区域较为规整，不同样本区域之间没有交错，当空间尺寸逐渐增大时，其精度会有提升。图像块尺寸越大，能提供的空间信息越丰富，越有利于提高分类精度。所以在图像块尺寸最大时，其精度最高。然而，过大的尺寸会导致计算成本和计算资源成倍增长，因此需要平衡精度和计算资源来选取合适的图像块尺寸。对于PU 数据集，其不同样本区域之间有交错。随着图像块尺寸增大，其总体准确度在上升，在尺寸为13×13 时达到最大，后续基本保持不变。对于Houston 数据集，各个样本区域比较分散，同一种样本分布也不集中；随着图像块尺寸增大，其包含的空间信息增多，总体分类精度在上升，尺寸在17×17 时精度达到最高。而尺寸为13×13 时，其精度比最高精度仅低了0.05%。

根据上述实验结果，从平衡计算资源和总体准确度出发，图像块尺寸统一为13×13。这样，一方面不需要过多的计算资源，另一方面还可以保持精度优势。

2.3 消融实验

为验证所提出的算法各个模块的有效性，在四个数据集上进行了消融实验，具体实验设置为：

基本网络：由1 个光谱特征学习模块和2 个空间特征学习模块构成。这些特征学习模块均采用了残差模块作为基础。

光谱注意力网络：由1 个包含了中心光谱注意力机制的光谱特征学习模块和2 个空间特征学习模块构成。也就是在基本网络的基础上，在光谱特征学习模块前加上中心光谱注意力机制。

光谱-空间注意力残差网络：由1 个包含了中心光谱注意力机制的光谱特征学习模块和2 个空间特征学习模块构成。在光谱特征提取结束后，空间特征学习前引入了空间注意力机制。

消融实验采取总体准确度（OA）作为评价指标，各个网络在四个数据集上的结果见表6。

表6 不同网络在四个数据集上的总体准确度Table 6 The overall accuracy of the different network on the four datasets

通过表6 可以发现，相比基本网络，光谱注意力网络在IP、SA、PU 和Houston 数据集上，精度分别提升了1.13%、0.53%、0.23%和1.85%。说明光谱注意力机制可以有效地改变各个波段的权重，对分类结果影响较大的波段给予较高的权重，影响较小的波段给予较小的权重，而基本网络默认各个波段的权重相同，由于不同类别都有其容易识别的波段，而不是整个波段都可以用来进行分类［14］，意味着每个波段对待分类样本的影响程度不同。

光谱-空间注意力残差网络相比光谱注意力网络在IP、SA、PU 和Houston 数据集上，精度分别提升了0.77%、0.95%、0.55%和0.84%，比基本网络精度分别提升了1.9%、1.48%、0.78%和2.69%，说明空间信息对于分类结果的有一定影响。引入空间注意力机制可以有效地调整周围像素对中心像素的影响，具体来说，周围像素对待分类的中心像素有帮助时，其相应的权重就会提高，能有效地增强后续网络所提取的光谱-空间特征。而对待分类的中心像素没有帮助或者负面作用时，其权重则会降低。

综上，所提出的各个模块对最后的分类结果都有积极的影响，能够有效提高总体分类准确度。

2.4 实验结果

本次实验中，选取了2D CNN［22］、3D CNN［23］、HybridSN［24］、RIAN［12］、SSFTT［25］这5 种方法作为对比算法，其中2D CNN、3D CNN、HybridSN、RIAN 都是基于CNN 的高光谱分类网络，而SSFTT 是基于视觉变换网络（Vision Transformer，ViT）的高光谱分类网络，这些算法都是当前较为有代表性的算法。

2.4.1 不同训练比例对实验的影响

考虑到所用到的4 个数据集中，只有Houston 数据集给出了标准的训练集和测试集划分，其余3 个数据集均没有标准划分，因此需要验证不同的训练集比例对各个算法的精度影响。在IP 数据集中，训练集样本占全部样本的比例为5%、10%、15%和20%。在SA 数据集中，训练集样本占全部样本的比例为0.5%、1%、1.5%和2%。在PU 数据集中，训练集样本占全部样本的比例为0.3%、0.5%、0.7%和1%。各个算法在不同比例的训练集中的总体准确度表现如表7～9 所示。

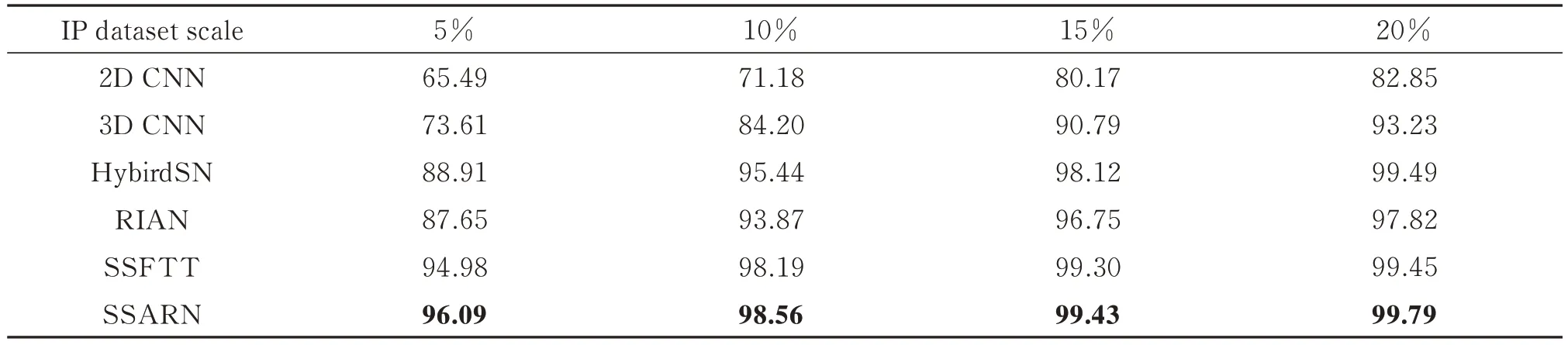
表7 不同网络在IP 数据集上的不同训练比例的总体准确度Table 7 The overall accuracy of the different network with different training ratios on the IP datasets

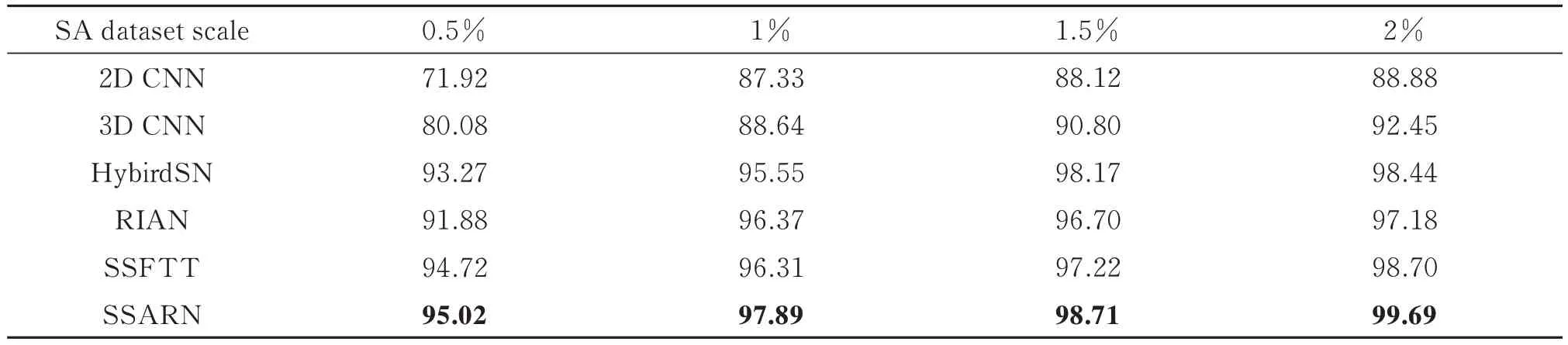
表8 不同网络在SA 数据集上的不同训练比例的总体准确度Table 8 The overall accuracy of the different network with different training ratios on the IP datasets

表9 不同网络在PU 数据集上的不同训练比例的总体准确度Table 9 The overall accuracy of the different network with different training ratios on the IP datasets

从表7～9 中可以看出，随着训练比例提高，各个算法总体准确度都在上升。而SSARN 在任何比例下都具有最高的精度，因此选择了各个算法精度最高的训练集比例，即IP 数据集每类随机选择20%的样本作为训练样本，SA 数据集每类随机选择2%的样本作为训练样本，PU 数据集每类随机选择1%的样本作为训练样本作为统一比较的基础。

2.4.2 对比算法在各个数据集上的结果

表10 展示了各个算法在IP 数据集上的各类别准确度、总体准确度（OA）、平均准确度（AA）和Kappa值。表中所展示的Kappa 值是在Kappa 计算公式（17）的基础上乘以100 进行展示。

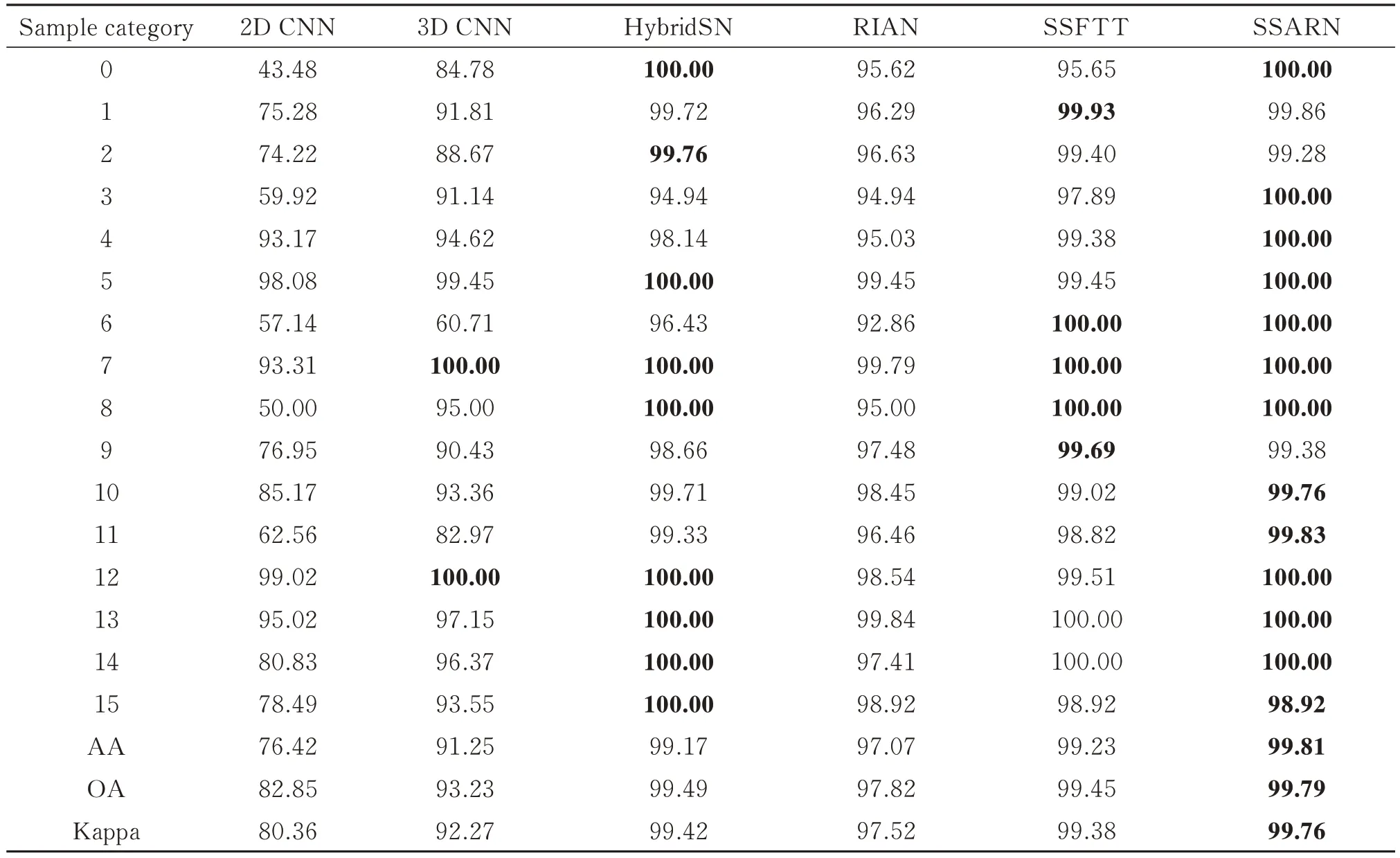
表10 不同算法在IP 数据集上的类别准确度、OA、AA 和KappaTable 10 The category accuracy，OA，AA and Kappa of the different algorithms on IP dataset

通过表10 可知，所提出的光谱-空间注意力残差网络SSARN，在AA、OA 和Kappa 系数上都取得了最佳的结果，并且在16 个类别精度中有12 个都达到了最好的效果，其中10 个各类的精度为100%。这说明SSARN 能够有效地学习不同类别的光谱特征和空间特征。在效果不好的4 个类别中，其训练样本分别是285 个、166 个、194 个和18 个，相比类别最少的训练样本4 个而言，其样本充足。也从侧面证明了SSARN 可以有效地解决样本分布不均匀带来的在少样本上精度较差的效果。而对于上述4 个效果较差的类别主要在两个不同样本区域的边缘，由于图像块包含了不同类别的样本，所学习的主要特征较少，最后分类的时候判断错误类别。

图12 展示了各个算法在IP 数据集上的分类效果。对比真值图（Ground Truth），2D CNN 和3D CNN 分类效果较差，而HybridSN、RIAN、SSFTT、SSARN 效果相对较好。2D CNN 和3D CNN 错误类别多集中在样本区域的内部，说明其对高光谱的空间特征没有有效地学习。而SSARN 算法相比HybridSN、RIAN、SSFTT 算法，判断错误的样本更少，更贴近真值图，说明该算法可以有效地学习高光谱图像的光谱特征和空间特征。

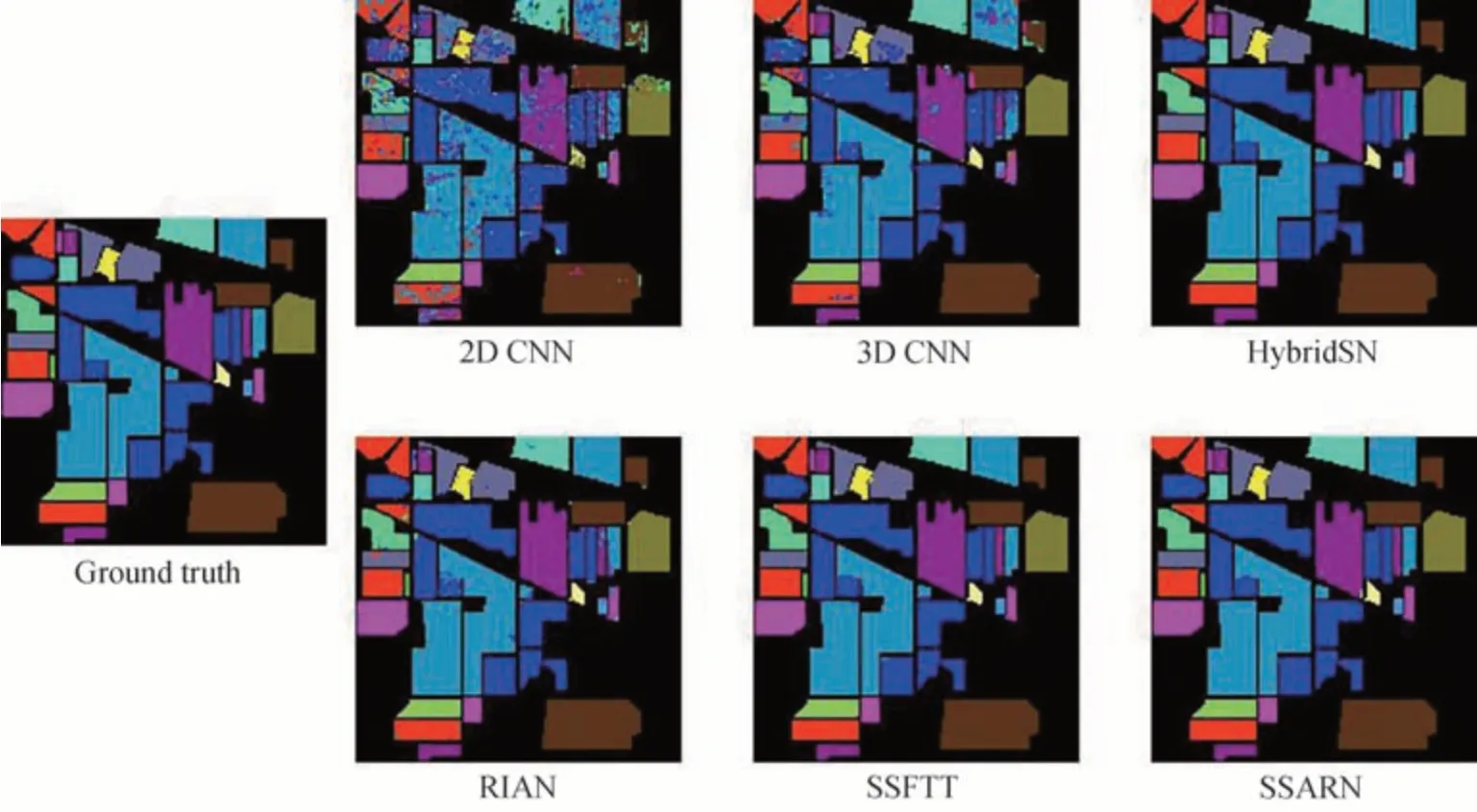
图12 各个对比算法在IP 数据集的效果Fig.12 The visualization result of each algorithm on the IP dataset

表11 展示了各个算法在SA 数据集上的各类别准确度、总体准确度（OA），平均准确度（AA）和Kappa 值。

表11 不同算法在SA 数据集上的类别准确度、OA、AA 和KappaTable 11 The category accuracy，OA，AA and Kappa of the different algorithms on SA dataset

从表11 可以看到，提出的SSARN 在OA、AA 和Kappa 值上均达到了最优值，在16 个类别精度中有12 个都达到了最好的效果，其中8 个类别精度为100%。这说明了该算法能够有效地学习不同类别的光谱特征和空间特征，而且面对不同数据集具有良好的泛化性。在效果相对不好的4 个类别中，其精度也分别达到了98.64%、99.97%、98.93% 和99.81%，相比最优效果，这4 个类别精度仅仅低了0.86%，0.03%、0.25% 和0.19%，差距并不明显。

图13 展示了各个算法在SA 数据集上的分类效果。对比真值图（Ground Truth），2D CNN、3D CNN、HybridSN、RIAN、SSFTT 的分类效果都不如SSARN。SSARN 分类错误的样本主要是第8 类，会被错误地分为第14 类，一方面是空间位置上这2 类较近，另一方面其他算法错误的分类也集中在第8 类，说明网络所提取第8 类的光谱特征与第14 类的光谱特征较为相近，进而出现了类别误判。

图13 各个算法在SA 数据集的效果Fig.13 The visualization result of each algorithm on the SA dataset

表12 展示了各个算法在PU 数据集上的类别准确度、总体准确度（OA）、平均准确度（AA）和Kappa 值。

表12 不同算法在PU 数据集上的类别准确度、OA、AA 和KappaTable 12 Category accuracy，OA，AA and Kappa of the different algorithms on PU dataset

从表12 可以看到，SSARN 在OA、AA 和Kappa 值上均达到了最优值，在9 个类别精度中有6 个都达到了最好的效果，其中2 个类别精度为100%。这说明了该算法能够有效地学习不同类别的光谱特征和空间特征，而且面对不同数据集具有良好的泛化性。在效果相对不好的3 个类别中，其精度也分别达到了94.13%、99.85%和94.81%，和最优的效果相比，分别低了3.42%、0.15%和3.08%，主要是第3 类和第6 类表现较差。分析其主要原因是第3 类和第6 类分散在全局中，集中区域较少，并且训练时选取的样本量也较少，因此网络提取特征时丢失了部分细节特征，从而导致其精度偏低。

图14 展示了各个算法在PU 数据集上的分类效果。对比真值图（Ground Truth），2D CNN、3D CNN、HybridSN、RIAN、SSFTT 的分类效果都不如SSARN。SSARN 算法判断错误的样本更少，更贴近真值图。

图14 各个算法在PU 数据集的效果Fig.14 The visualization result of each algorithm on the PU dataset

表13 展示了各个算法在Houston 数据集上的类别准确度、总体准确度（OA）、平均准确度（AA）和Kappa 值。

表13 不同算法在Houston 数据集上的类别准确度、OA、AA 和KappaTable 13 The category accuracy，OA，AA and Kappa of the different algorithms on Houston dataset

从表13 可以看到，SSARN 在OA、AA 和Kappa值上均达到了最优值，在15 个类别精度中有11 个都达到了最好的效果，其中3 个类别精度为100%。这说明该算法能够有效地学习不同类别的光谱特征和空间特征，而且面对不同数据集具有良好的泛化性。在效果相对不好的4 个类别中，相比最优的效果，精度低了1.32%、52.12%、4.84%和4.57%。效果最差的是类别9，即高速公路（Highway）这一类别。绝大多数对比算法在这一类表现都很差，而对比算法HybirdSN 在这一类达到了100%的精度，分析主要原因可能是数据预处理阶段，只有HybirdSN 利用PCA 进行数据降维，保留了主要的光谱特征，而其他算法都是在原始的光谱维度上进行特征学习，冗余的光谱波段会导致网络学习该类别的光谱能力下降，进而导致在该类别上精度下降较多。

图15 展示了各个算法在Houston 数据集上的分类效果。对比真值图（Ground Truth），2D CNN、3D CNN、HybridSN、RIAN、SSFTT 的分类效果都不如SSARN。SSARN 分类错误的样本主要是第9 类，其他算法错误的分类也集中在第9 类。冗余的光谱特征会导致网络对某些类别产生过拟合，进而导致其分类精度下降。总体来看SSARN 算法相比其他算法，判断错误的样本更少，更贴近真值图。

图15 各个对比算法在Houston 数据集的效果Fig.15 The visualization result of each algorithm on the Houston dataset

3 结论

本文提出了基于光谱-空间注意力残差网络（SSARN）的高光谱分类方法，该方法利用中心区域光谱注意力机制，在保留全部光谱信息的基础上，对光谱之间的权重进行了调整，避免了网络提取光谱特征时认为各个通道权重一致的问题。重新调整光谱权重后，采用了残差网络对光谱维度进行特征提取，一方面可以有效地提取和保留光谱信息，另一方面便于优化网络。在提取光谱特征后，利用空间注意力机制对空间-光谱特征进行学习，使后续的空间特征学习模块更多地关注输入中的相关空间特征，尽可能多地提取有用的空间特征来帮助分类。空间特征学习模块采用2 个类似的残差特征提取模块，主要是因为空间信息相比光谱信息更多，需要更多的网络参数进行学习。在4 个公开的数据集上，消融实验证明了各个模块的有效性。和常用以及最新算法相比，所提出的SSARN 在所有数据集上都达到了最好效果，也证明了该网络的有效性和鲁棒性。

但是该算法面对分散样本时，其特征提取能力以及判别能力出现了下降，一方面是因为所提出的网络都是基于图像块输入的，对上下文信息的获取较差；另一方面类别分散在全局中，样本比例的不均衡性会导致网络提取特征时，分散类别样本特征权重较低，可能导致其重要的特征丢失。考虑到视觉变换模型对图像全局信息的把握能力更强，后续可以考虑用Transformer 网络，并根据样本不均衡引入动态权重调整系数调整小样本的特征权重来解决全局分散样本精度较低的问题。