基于相干合成涡旋光束光场分布角向不变性的评价函数构建及其应用研究

秦广为，谢文科，邹行健，于涛，谢巧

（1 中南大学 物理学院，长沙 410083）

（2 深圳北理莫斯科大学 材料科学与工程学院，深圳 518172）

0 引言

涡旋光束凭借其独特的螺旋相位分布和携带轨道角动量（Orbital Angular Momentum，OAM）的特性，成为目前的研究热点［1-2］。相较于传统方法生成的涡旋光束，相干合成涡旋（Coherent Synthetic Vortex，CSV）光束具有输出功率高、拓扑荷模式可控等优点，其在目标转速遥感、光通信等远距离传输领域具有广泛的应用前景［3-4］。2021 年，侯天悦等通过相干合成光纤阵列，生成了高功率、快速、模式可切换的叠加态涡旋光束，并提出可将CSV 光束引入光通信领域［5］；2022 年，于涛等利用相干合成技术生成了±l阶拓扑荷的叠加态涡旋光束，建立了目标转速远距离探测模型［6］。但在远距离大气探测应用中，由于大气湍流的存在，CSV 光束会发生波前畸变而导致光斑畸变和OAM 模式扩展，即光束质量产生劣化，故需对CSV 光束进行自适应光学校正。由于随机并行梯度下降（Stochastic Parallel Gradient Descent，SPGD）算法具有收敛速度快、收敛精度高等优点，被广泛应用于无波前传感的自适应光学系统［7］。

SPGD 算法性能优劣很大程度上依赖于评价函数选取的准确性，然而由多拓扑荷组成的叠加态CSV 光束，其光强和相位分布较为复杂，传统评价函数应用于CSV 光束的质量评价存在困难。例如，斯特列尔比（Strehl Ratio，SR）、桶中功率（Power-in-the-bucket，PIB）被广泛应用于相干合成光束质量评价，但由于CSV 光束具有中空环形的光强分布特征，其不能直接用于CSV 光束质量评价［8-9］。光强相关系数、OAM 模式能量占比虽可以应用于CSV 光束质量评价，但以光强相关系数作为评价函数应用于SPGD 波前畸变校正时，因CSV 光束的光强分布会随传输距离变化发生较大改变，在实际应用中难以获取真空条件下的光强分布（标准光斑）［10］；以OAM 模式能量占比为评价函数进行波前校正时，由于对CSV 光场进行了螺旋谱分析［11］，导致SPGD 算法收敛时间过长，校正后光束质量难以满足应用要求。为有效实现基于SPGD 算法的CSV 光束波前畸变SPGD 自适应光学校正，需构建适用于CSV 光束的评价函数。

因此，本文基于CSV 光束传输过程中光场分布的角向不变特性，以角向条纹对比度构建了CSV 光束的质量评价函数JD，并结合SPGD 算法进行了波前畸变自适应校正。相较于评价函数光强相关系数和OAM模式能量占比，构建的评价函数JD可以有效提升SPGD 算法的收敛精度和收敛速度，并且在复杂双环阵列结构的CSV 光束SPGD 波前畸变校正中仍然有效。

1 CSV 光束传输特性及其评价函数

1.1 CSV 光束模型及传输特性

如图1 所示，将N个振幅归一化的高斯光束以环形排布在z=0 平面。为相干合成高功率涡旋光束，对该环形排布的高斯光束阵列施加l0阶离散涡旋相位，其光束阵列在任意z处的光振幅［12］为

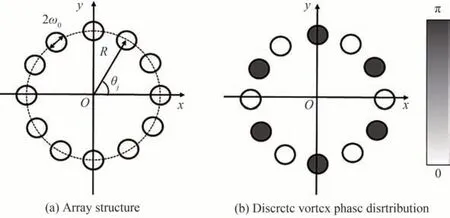
图1 N=12，l0=6 时的光束阵列示意图Fig.1 The schematic diagram of the CSV beam array where N=12，l0=6

式中，R为组束环半径，k为波数矢量；(r，φ，z)为距离z处的平面极坐标；是传输至距离z处的光斑半径宽度，ω0为源平面处高斯光束束腰半径，为共焦参数；R(z)=z+f2/z为z处的曲率半径；N为子光束数目；θj=2πj/N为第j个高斯光束中心与x轴的夹角；l0为目标拓扑荷。

式中，lp=l0-Np，其中p为任意整数。由式（2）可知，CSV 光束中除存在目标拓扑荷外，还存在拓扑荷数为l0-Np（p≠0）的其它模式，即拓扑荷发生了扩散，并且各阶模式振幅大小正比于所对应拓扑荷阶数的贝塞尔函数幅值。其中lp阶模式振幅为

当目标拓扑荷l0=±N/2 时，CSV 光束中±l0阶OAM 模式占比最强，此时光场表达式近似为

1.2 传统评价函数

为保证SPGD 波前畸变校正的有效性，评价函数不仅要求计算简便、易于获取，还应满足在相位畸变为零时存在唯一的全局极值［14-15］。分析已有光束质量评价函数应用于CSV 光束的可行性。

1）斯特列尔比

斯特列尔比定义为实际光束的远场峰值光强与具有同样功率的理想光束的峰值光强之比［8］，可以表示为

式中，I0(x0，y0)为理想光束的峰值光强大小，I(x0，y0)实际光束的远场峰值光强，(x0，y0)为峰值光强位置。

SR 不仅可在一定程度上反映光束的能量聚集度，还可以反映光束波前相位误差的大小。但对于涡旋光束而言，由于其具有空心环形的强度分布，故难以准确获得峰值光强位置(x0，y0)。

2）桶中功率

桶中功率表征光束的能量集中度，其定义为在远场给定尺寸的“桶”中包围的激光功率占总功率的百分比［9］，即

式中，C为所划分的“桶”的尺寸大小，I(r，φ)为扰动下的远场光强分布。由式（2）定义可知，具有相反拓扑荷的涡旋光束光斑尺寸相同，故桶中功率无法直接应用于叠加态涡旋光束的质量评价。

3）光强相关系数

涡旋光束中模式纯净度与光强相关系数呈正比关系［16］。基于光强相关系数的评价函数定义为［17］

式中，Iid(r，φ)为无湍流传输时的远场光强分布。

由式（7）可知，光强相关系数JC作为评价函数时，需以无湍流时的理想光强分布Iid(r，φ)作为模板函数，用以计算当前光强分布I(r，φ)与Iid(r，φ)的相似性。然而CSV 光束光强分布随远场传输距离发生改变，因此在实际应用过程中无湍流传输时的远场光强分布Iid(r，φ)获取困难。

4）OAM 模式能量占比

依据螺旋谐波分析方法，可将涡旋光场分解为一系列具有不同拓扑荷数的模式叠加［11］，即

式中，al为第l阶拓扑荷模式对应的振幅大小，即

对al径向积分可得

Pl为第l阶OAM 模式的强度大小。因此，以±l阶OAM 模式能量占比定义的评价函数可表示为

由式（8）～（11）可知，JO获取过程包含了复杂的积分运算，所需时间较长。

1.3 角向条纹对比度评价函数构建

鉴于上述光束质量评价方法存在模板函数获取困难、计算时间长等缺陷，不能较好地满足CSV 光束的质量评价及其实际应用需求。结合CSV 光束传输特性，构建光斑角向条纹对比度评价函数。

由式（2）可得，CSV 光束在距离z处的光强分布为

式中与角度有关的因子为

由式（13）可知，CSV 光束光强随角度呈明暗周期分布，如图2 所示，其中红线标注的区域表示明条纹区域，黄线标注的区域表示干涉暗场分布区域，并且当l0确定时，该周期分布特性仅与幅角φ的变化有关，与传输距离无关。

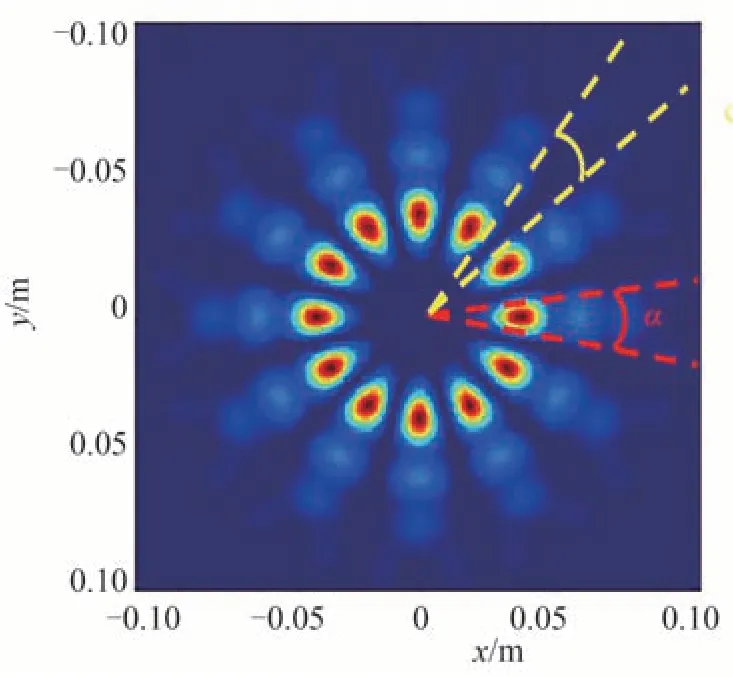
图2 CSV 光束角向特性Fig.2 The angular characteristic of CSV beam

在SPGD 算法中，所测CSV 光束的光强分布特性可以用像清晰度函数进行描述［18］。因此，在CSV 光束的SPGD 波前畸变自适应校正中，采用角向条纹对比度结合像清晰度函数的方法进行光束质量评价。其中像清晰度函数表示为

式中，基于干涉条纹的角向周期分布规律构建的模板函数M(r，φ)为

M1、M2分别表示CSV 光束明、暗条纹所在区域对应的模板函数，其反映了CSV 光束的周期分布特性；α表示明暗干涉条纹区域选取的角向范围大小。在SPGD 校正系统中，分别测量明暗条纹区域的总光强，即可构建角向条纹对比度评价函数为

2 基于JD评价函数的CSV 光束自适应光学校正

仿真参数设置如下：种子光源波长为1 064 nm，子光束束腰半径ω0=5 mm，阵列半径R=30 mm；光束的传输距离z=1 km，子孔径数目N=12，大气结构常数Cn2=1×10-14m-2/3；在MATLAB 仿真过程中，空间采样分辨率为512×512。

利用随机相位屏模型模拟大气湍流所产生的畸变相位。如图3 所示，将光束传输路径等分为M段，每一段路径等效为光束通过一个“薄”相位屏。光束从zm平面传输到zm+1平面表示［19-20］为

图3 湍流相位屏传输模型Fig.3 Transmission model of atmosphere phase screens

式中，u(r，zm)、u(r，zm+1)分别为传输至zm和zm+1平面处的光场；F为傅里叶变换，F-1为傅里叶逆变换；k为光束的波束矢量，kx，ky分别为在x方向和y方向上的空间波数；φ(r，zm)为根据大气湍流Kolmogorov 谱的功率谱密度函数得到随机相位分布［21-22］。

2.1 CSV 光束传输特性分析

1 km 处CSV 光束的光强分布和OAM 模式能量分布结果如图4 所示。其中图4（a）和（c）是无湍流传输时的光强分布和OAM 模式分布。由图4（a）可知，CSV 光束经自由空间传输后，由于相邻子光束之间会产生光场叠加，因而形成12 条随角度周期性变化的瓣状干涉条纹，且能量集中分布于瓣状条纹中心位置。由图4（c）可知，加载了l0=6 阶离散涡旋相位的CSV 光束中主要包含±6 阶OAM 模式，其占比之和为0.982。图4（b）为受到湍流扰动后的光强分布，由于大气传输波前畸变效应，此时的明暗条纹周期分布规律被破坏，亮条纹的强度亦不均匀。图4（d）为受湍流扰动后的CSV 光束中各阶模式占比分布，此时±6 阶OAM 模式能量向邻近模式发生扩散，其占比之和下降至0.167。因此，大气湍流带来的波前畸变限制了CSV 光束在遥感探测等领域的应用，故需对CSV 光束进行波前畸变校正。

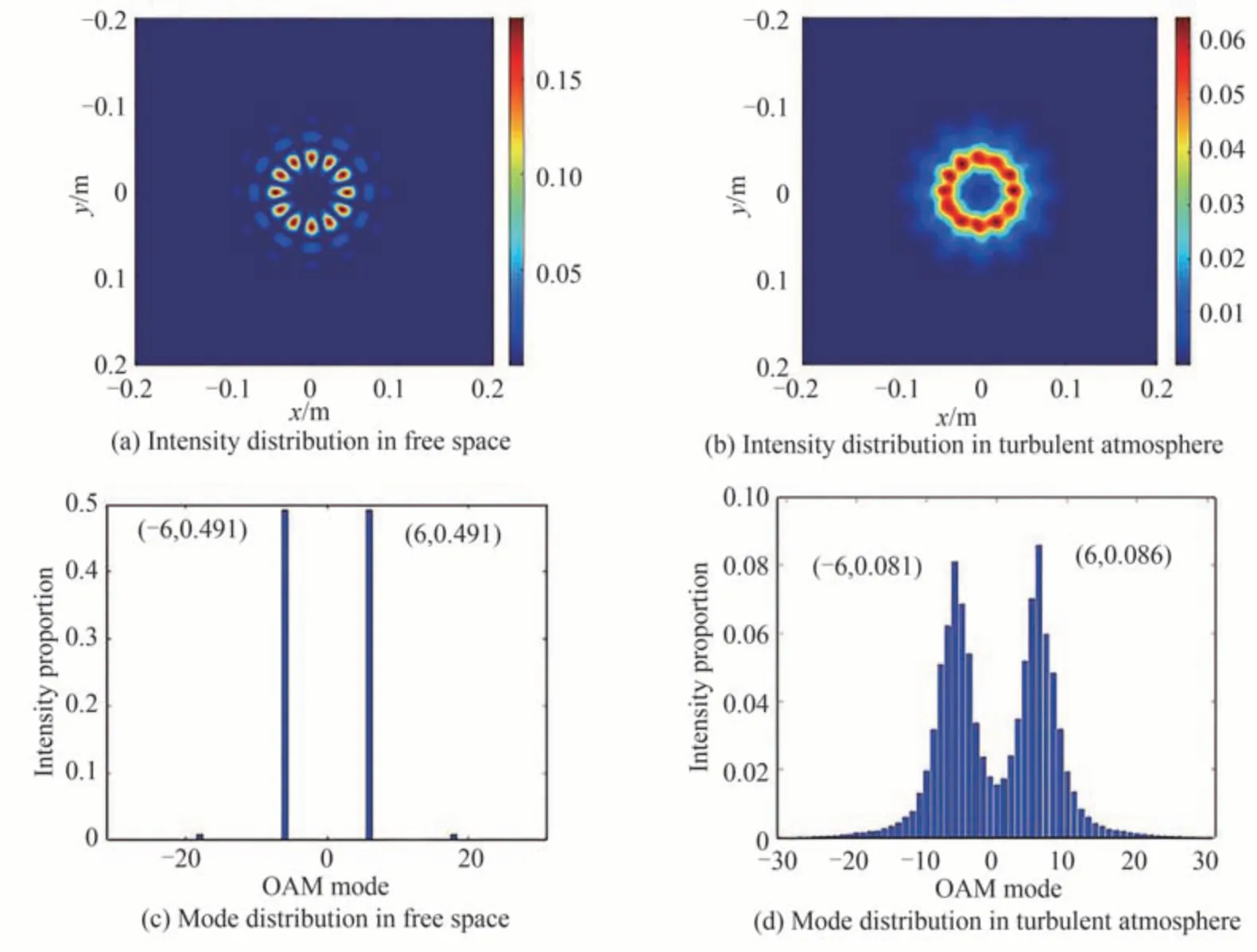
图4 远场光强分布和OAM 模式分布Fig.4 Far-field intensity distribution and OAM mode distribution

2.2 角向区域选取

JD作为评价函数时，选取的明暗条纹角宽度α将影响SPGD 算法性能。当l0=6 时，α的取值范围为0°～15°。受限于所设空间分辨率大小，α的最小取值间隔为，即1.41°。在Cn2=1×10-14m-2/3的湍流条件下生成200 组湍流相位屏。以1.41°为步长改变α的取值，并在每一α的取值下依据上述湍流相位屏进行相同的200 次校正实验，由所测平均结果分析α对SPGD 算法性能的影响。

图5 为200 次校正实验中JD的平均收敛曲线，当α由1.41°增大至14.1°时，JD收敛极值由0.774 7 递减至0.471 2，表明α取值越小，JD对于CSV 光束中明暗条纹分布变化越敏感，CSV 光束的质量评价越准确，SPGD 算法的收敛精度越高。SPGD 算法收敛速度随α变化关系如表1 所示，将收敛步数定义为评价函数由初态收敛至距极值80%处所经历的步数。由表1 可知，随着α增大，计算的所需采样点数越多，单次迭代所需时间增加的同时收敛步数基本不发生改变。因此，当增大α时，SPGD 算法的收敛速度下降，可以通过降低α值来有效提升SPGD 算法的收敛速度和收敛精度。后续实验中α选取为1.41°。

表1 SPGD 算法收敛速度随α 变化关系Table 1 Variation of convergence speed with α in SPGD algorithm

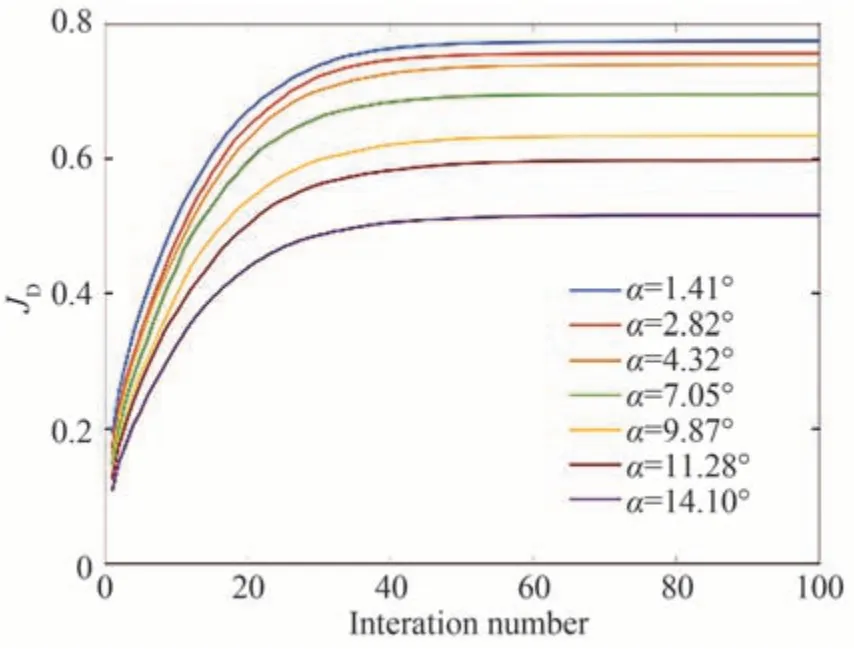
图5 α 取不同值时的JD收敛曲线Fig.5 Convergence curve of JD under different α

2.3 校正结果分析

为研究以JD作为评价函数的SPGD 算法的校正性能，分别选用JO、JC以及JD作为CSV 光束评价函数，结合SPGD 算法进行波前畸变校正，并以校正后的光强分布和±6 阶OAM 模式能量占比评价CSV 光束的SPGD 波前畸变校正效果。在Cn2=1×10-14m-2/3的湍流条件下生成200 组湍流相位屏，分别采用三种评价函数进行了相同的200 次重复实验。

在波前畸变校正实验中，归一化后的评价函数随迭代次数的收敛曲线如图6 所示。在平均收敛曲线中，校正前JO、JC、JD的取值分别为0.154、0.552、0.575；在校正过程中，三种函数均以单调递增的方式进行收敛；曲线收敛后的三种评价函数取值分别为0.355、0.851、0.877。比较JO、JC、JD在200 次实验中收敛极值的波动幅度可知，JO的极值波动幅度为0.606，明显大于JC的0.239 和JD的0.152，表明采用JO的SPGD 算法稳定性差。表2 为采用不同评价函数的SPGD 算法敛速度分析，其中由于JD相较于JC、JO运算更简便、计算所需采样点数更少，单次迭代所需时间仅为0.5 ms，相较于JO和JC单次迭代速度分别提升8.2 倍和3.0 倍。计算不同评价函数由初态收敛至距极值80%处所经历的步数可知，JO、JC、JD的收敛步数分别为56 步、41 步和36 步；经由MATLAB 计算迭代总时间可知，JD相较于JO、JC收敛速度分别提升12.7 倍和3.4 倍。因此，采用JD作为评价函数可以有效提升SPGD 算法的校正速度。

表2 评价函数收敛速度分析Table 2 Analysis of metric function convergence speed

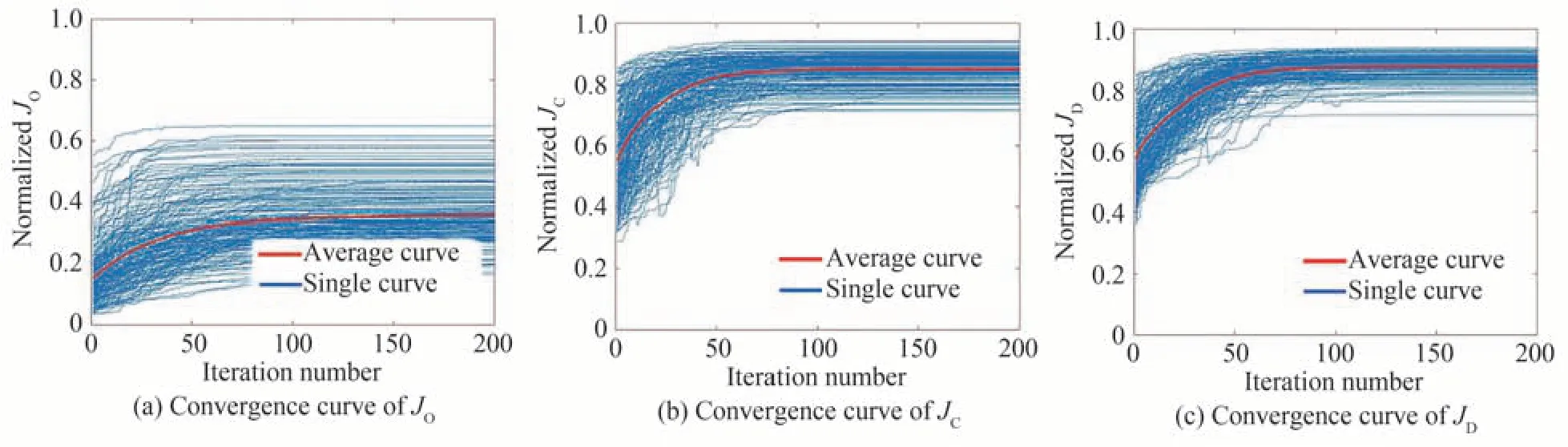
图6 JO、JC、JD评价函数的收敛曲线Fig.6 Convergence curve of JO，JC and JD

校正后光强分布和OAM 模式分布如图7 所示。图7（a）和（c）为采用JO作为评价函数的校正结果，其中图7（a）为校正后光强分布，此时光强分布与图3（b）中校正前光强分布相近似，表明光束的波前相位仍存在较大校正残差；图7（d）为校正后OAM 模式分布，以JD评价函数校正后的±6 阶OAM 模式能量占比之和由0.167 提升至0.363。图7（b）、（c）分别为采用JCov、JD作评价函数校正后的光强分布，在图7（b）、（c）中均可清晰地观测到干涉条纹的明暗分布成角向周期性分布，同时光强集中分布于瓣状条纹中心亮斑区域，表明了JC、JD能够改善CSV 光束的光强分布。图7（e）、（f） 分别为采用JC、JD作评价函数校正后的OAM 模式分布，其中JD校正后±6 阶OAM 模式能量占比之和为0.229，相较于采用JC的0.224 提升幅度更大，表明JD相较于JC能够更有效地提升模式纯度。

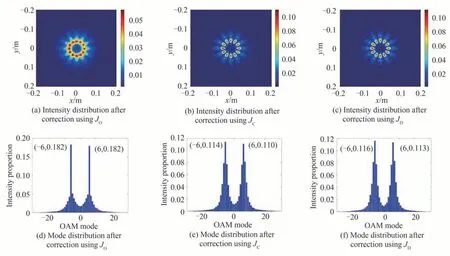
图7 采用JO、JC、JD作为评价函数的SPGD 波前畸变校正结果Fig.7 The results of SPGD wavefront phase correction using JO，JC and JD as metric function

综合比较校正后CSV 光束光强分布和OAM 模式能量分布，其中JO能够显著提升校正后±6 阶OAM 模式能量占比，但其校正后光强分布几乎没有得到优化，因此以JO作为评价函数的SPGD 算法在波前畸变校正中对于CSV 光束质量改善效果较差；采用JC、JD校正后光束光强分布均存在清晰的干涉条纹分布，但JD校正结果中，±6 阶OAM 模式能量占比优于JC。因此，以JD作为评价函数的SPGD 算法可以更好地提升CSV光束质量，具有更高的校正精度。

综上，JD作为评价函数可有效提升SPGD 算法的校正性能，使其具有更高的收敛精度和更快的收敛速度。

2.4 双环阵列结构的CSV 光束波前相位校正

在实际应用中，为获取更高的输出功率，CSV 光源阵列通常为更加复杂的多环嵌套结构［5］。为验证评价函数JD在复杂光源阵列中的有效性，构建了如图8 所示的双环阵列结构CSV 光源，并结合SPGD算法进行波前畸变自适应校正。研究表明，CSV 光束中OAM 模式分布与光源阵列结构填充因子f=ω0/[Rsin(n/N)]相关［23］。因此，为保证双环阵列结构的CSV 光束同单环结构的OAM 模式分布相同，应使内外环具有相同的填充因子，故将双环阵列结构参数设置为：ω01=3 mm，ω02=5 mm，R1=18 mm，R2=30 mm；内外环均加载6 阶拓扑荷的离散涡旋相位。以该光源结构进行1 km 大气传输的仿真结果见图9。

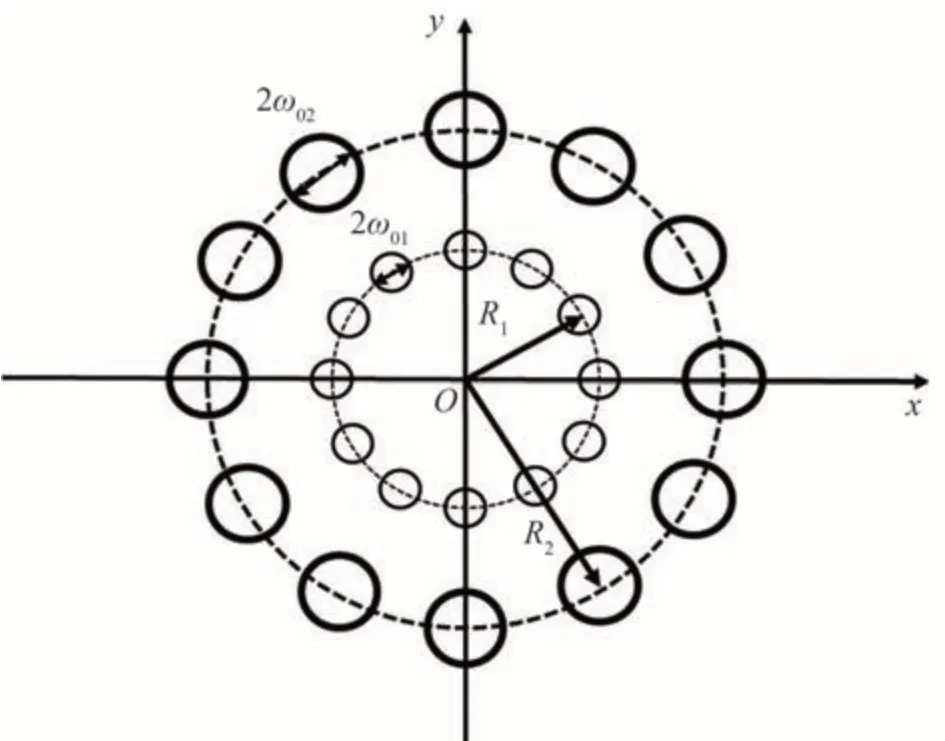
图8 双环阵列结构示意图Fig.8 The schematic diagram of dual-ring array

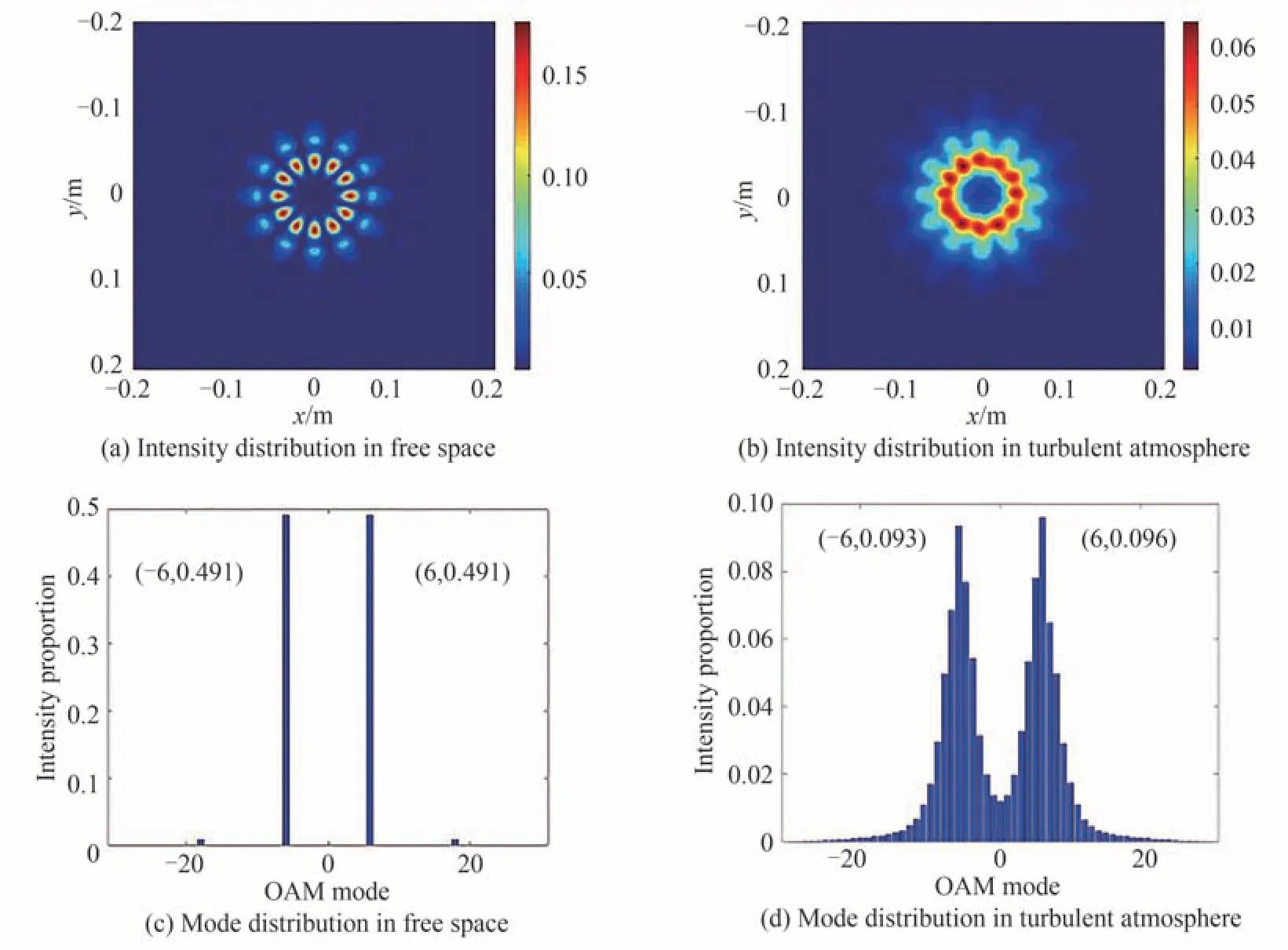
图9 双环阵列CSV 光束的远场光强分布和OAM 模式分布Fig.9 Far-field intensity distribution and OAM mode distribution of CSV beam with dual-ring array

1 km 处CSV 光束的光强分布和OAM 模式能量分布结果如图9 所示。图9（a）、（c）分别为理想条件下的光强分布和OAM 模式分布，此时光强分布具有清晰可见的周期性瓣状干涉条纹，且能量汇集于瓣状光斑中心位置，表明了双环阵列的CSV 光束光场分布与单环具有相同的角向周期性。图9（b）、（d）为受大气湍流扰动后的光强分布和OAM 模式分布，对比图9（a）、（c）可知，经过大气传输后，CSV 光束的光强分布角向规律性消失，明条纹之间相互重叠并成环形分布，以致角向条纹对比度下降；±6 阶OAM 模式能量占比之和由0.982 大幅跌至0.189，±6 阶OAM 模式能量向邻近模式发生扩散。

双环CSV 光束经SPGD 算法校正后光强分布和OAM 模式分布如图10 所示。其中图10（a）、（d）为采用JO作为评价函数进行SPGD 波前校正后的结果，对比图9（b）、（d）可知，JO作为评价函数进行SPGD 波前校正可以有效提升双环CSV 光束中±6 阶OAM 模式能量占比，但其对于CSV 光束的光强分布几乎没有明显改善。采用JC、JD作为评价函数进行波前相位校正后的光强分布比较结果如图10（b）、（c）所示，其中CSV 光束光强分布在校正后具有清晰的明暗条纹分布规律并且能量汇聚于瓣状光斑中心，因此JC、JD能够改善CCV光束的光强分布。采用JC、JD进行SPGD 波前校正后的OAM 模式能量分布见图10（e）、（f），其中采用JC、JD作评价函数进行校正后±6 阶OAM 模式能量占比之和分别为0.229、0.238。分析可知，在更加复杂的CSV阵列结构中，采用JD作为评价函数的SPGD 算法仍可有效进行波前畸变校正。

图10 双环阵列CSV 光束波前相位校正结果Fig.10 The results of wavefront phase correction for CSV beam with dual-ring array

3 结论

为提升经过大气传输后的CSV 光束质量，以CSV 光束的传输特性为基础，构建了角向条纹对比度评价函数JD，结合SPGD 算法对CSV 光束的波前畸变进行了校正。仿真结果表明，相较于光强相关系数JC、OAM 模式能量占比JO，以JD作为评价函数的SPGD 算法在过程中具有更高的收敛精度和更快的收敛速度，其在单环结构CSV 光束波前校正结果中，CSV 光束的角向条纹对比度由0.575 提升至0.877；模式能量占比由0.167 提升至0.229；相较于JO、JC，收敛速度分别提升了12.7 倍和3.4 倍。此外，在复杂双环阵列结构的CSV 光束中，以JD作为评价函数的SPGD 算法仍可在CSV 光束的波前畸变自适应校正中有效改善CSV 光束的光强分布以及±6 阶OAM 模式能量占比，从而提升CSV 光束质量。所提出的评价函数JD可以较好地满足CSV 光束的质量评价及其实际应用的需求。