时空大数据驱动的页岩气钻井成本动态建模与优化

杨天翔 徐海棠 段言志 陈江燕 马英恺 李 庆

（1.中国石油西南油气田公司天然气经济研究所，四川 成都 610051；2.中国石油西南油气田公司，四川 成都 610051；3.中国石油西南油气田公司燃气分公司，四川 成都 610051）

0 引言

近年来全球能源需求不断增长，对清洁能源和减少碳排放的需求日益旺盛，页岩气作为一种广泛存在的非常规能源资源备受关注。页岩气勘探与开发被认为是能源转型和能源自给自足的重要战略举措之一。然而，由于其特殊性和开发技术的挑战性，我国页岩气开发投资风险较高，钻井成本居高不下已成为制约页岩气产业发展的关键因素。页岩气钻井成本在整个开发过程中占据重要地位，直接影响着页岩气产业的经济可行性和可持续发展。受制于目前技术水平和市场状况，并且缺乏完善的成本评估模型和决策支持工具，钻井成本的控制和优化面临许多挑战。

通过对页岩气钻井成本影响因素的研究，提升钻井成本分析预测的准确性和可靠性，并为钻井成本的优化与决策提供有效支持。笔者通过收集和分析多源数据，包括工程参数数据、时间维度数据和空间维度数据等，运用多种机器学习算法对钻井成本进行综合分析建模，有助于揭示钻井成本的变化趋势和影响因素，并为决策者提供优化建议。在研究方法方面，笔者基于时空大数据建立LSTM（Long Short-Term Memory）模型和SVM（Support Vector Machine）模型对页岩气钻井成本进行动态建模，在时间和空间维度上提供更准确和可靠的预测结果。此外，采用Stacking方法对模型进行融合和验证，进一步提高预测能力和泛化能力，以有效应对时空异质性的挑战。模型建立之后，笔者采用四川盆地页岩气564 口页岩气开发井及31 口页岩气评价井的钻井数据进行模型验证，实验结果表明模型具有较好的仿真及预测效果，能够为页岩气钻井成本的分析和优化提供决策依据，并为大数据驱动决策支撑的研究方向提供有益的启示。

1 页岩气钻井成本影响因素分析

1.1 数据采集与特征工程

为了对页岩气钻井成本的影响因素进行详细分析，首先需要进行数据的收集和特征工程构建。这一步骤旨在获取可靠的数据来源，并对原始数据进行清洗、转换和标准化，获得用以分析成本影响因素的数据集，以确保后续分析的准确性和可靠性。以四川盆地近8 年（2015-2022）564 口页岩气开发井及31 口页岩气评价井为样本，数据采集的主要渠道包括企业内部与页岩气钻井相关的工程数据、施工参数、成本数据等及来源于研究机构、政府统计局、行业咨询公司的宏观经济指标等时间维度数据和地质条件等空间维度数据共45 多项，33 200 余条。构建时空大数据集如表1所示。

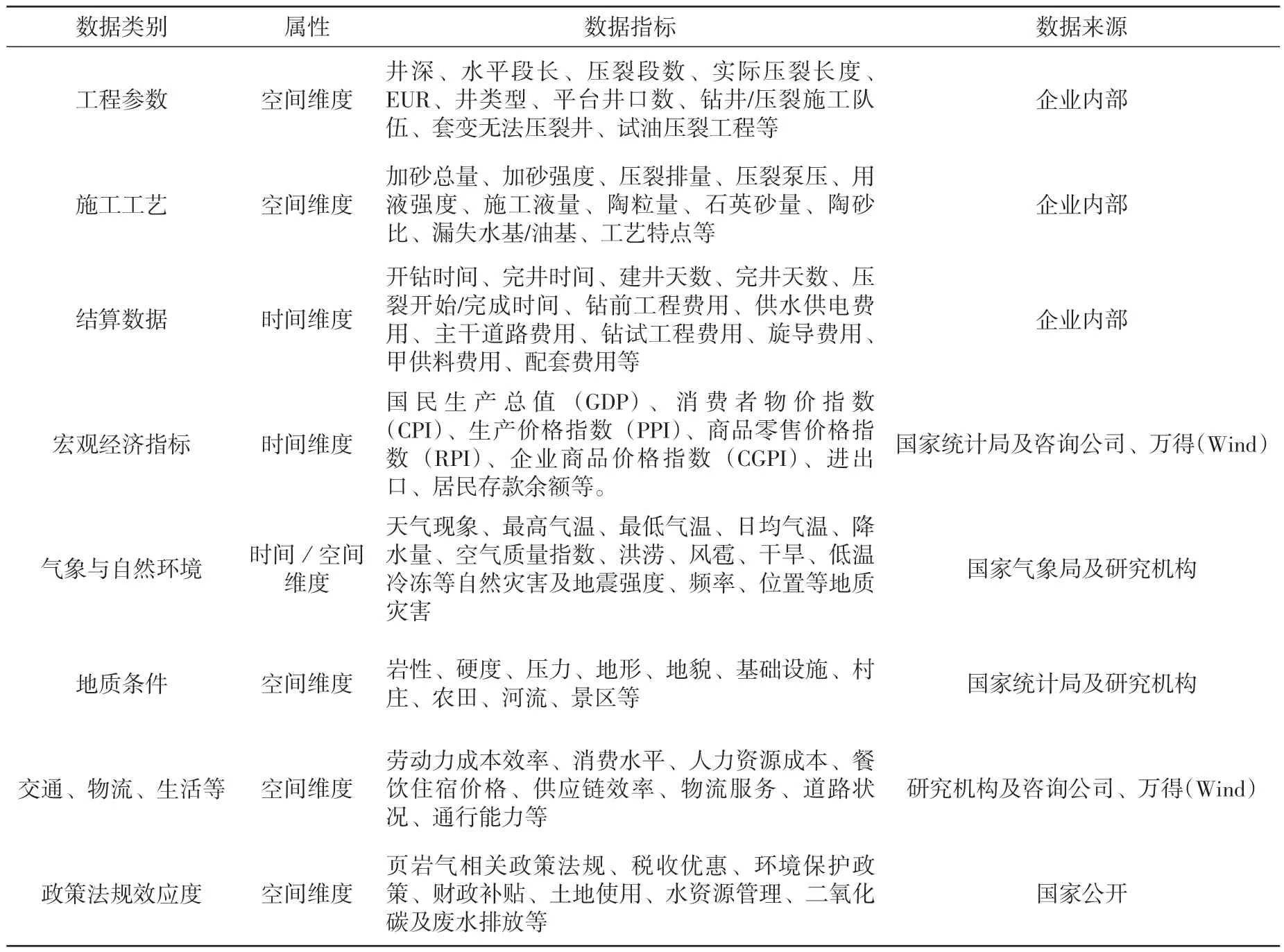
表1 页岩气钻井成本影响因素分析时空大数据集表

完成时空大数据集的构建后，通过数据清洗和转换，对数据进行去重、缺失值处理、异常值检测、结构化、差值、标准化等操作。然后利用特征选择、转换、组合、构造，提取数据特征，使得数据集更具代表性和可解释性。

1.2 页岩气钻井技术进步指数（GTPI）测算

随着页岩气钻井规模的扩大以及钻井数量和资源开发量的增加，往往可以实现经济的规模效益开发。规模效应下降导致单位钻井成本下降。同时页岩气钻井也被许多企业实践证明存在典型的学习曲线效应，为了更准确地刻画页岩气钻井的成本特征，引入页岩气钻井技术进步指数（GTPI）来表征规模效应和学习曲线效应对页岩气钻井成本的影响。

采用规模效应因子（SEF）来度量钻井规模对成本的影响，采用学习曲线因子（LCF）来度量随着经验的积累和技术的改进，作业效率提高对成本的影响。整合规模效应因子（SEF）和学习曲线因子（LCF），通过公式（1）计算页岩气钻井技术进步指数（GTPI）。

其中，规模效应因子（SEF）可基于钻井规模和资源开掘量的历史数据进行拟合估算，学习曲线因子（LCF）可以通过分析钻井经验和历史钻井数据评估。根据样本595口井计算出的GTPI如图1所示。

图1 2015-2022年样本钻井技术进步指数图

考虑钻井规模效应和学习曲线效应对成本的影响，可引入页岩气钻井技术进步指数（GTPI），能够更准确地刻画页岩气钻井成本的动态特征，也有助于企业进行成本分析和未来成本预测，以支持决策制定和成本优化的相关措施。

1.3 基于GBDT模型的影响因素分析

为了分析对页岩气钻井成本的主要影响因素，基于上述时空大数据集，建立梯度提升决策树（Gradient Boosting Decision Tree，GBDT）模型来对页岩气钻井成本影响因素及影响程度进行量化及解释。主要分为4 个步骤：①初始化模型：选择一棵基本回归树作为初始模型。②损失函数定义：选择适当的损失函数来度量模型拟合效果和预测误差。对于回归问题，常用的损失函数包括均方误差（MSE）和平均绝对误差（MAE）等。③训练模型：通过迭代的方式，逐步优化模型。每一轮迭代中，计算当前模型的残差，并通过拟合一颗新的回归树来减少残差。然后将新生成的树与之前的树相加，得到新的模型。④终止条件：根据预先设定的停止准则来决定模型训练的终止，例如达到预定迭代次数或残差下降到一定阈值。GBDT模型原理如图2所示。

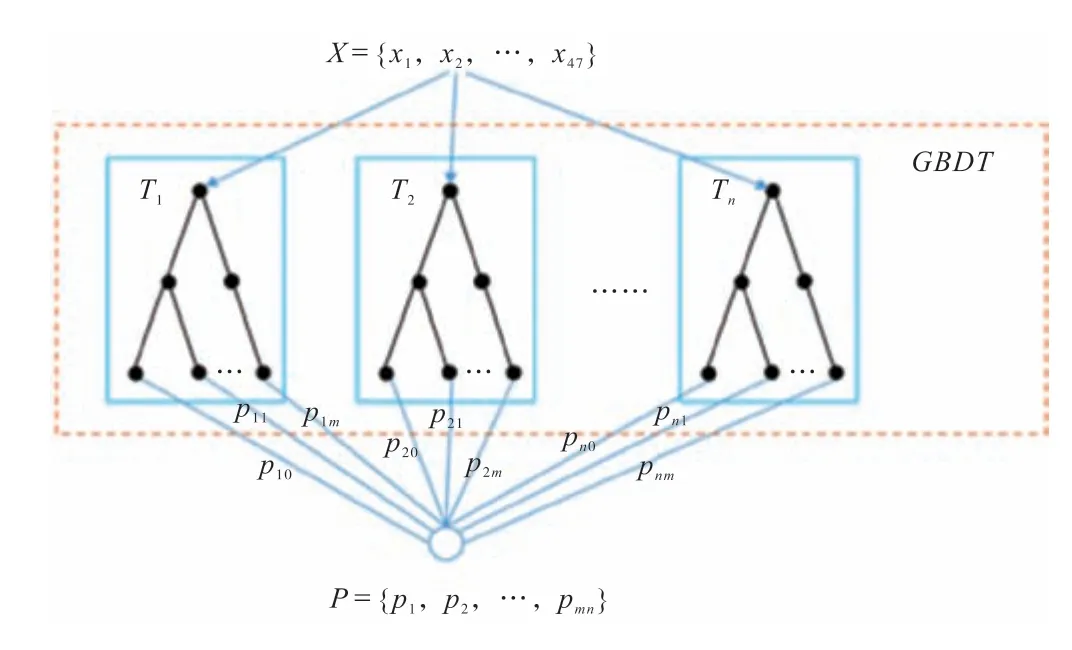
图2 梯度提升决策树（GBDT）算法原理图

采用Python 语言中的Scikit-learn 机器学习库实现，将数据集中各指标项均进行归一化无量纲处理，对成本指标按每千米归一，对宏观经济指数指标统一按照2000年数值标准化为100换算，按照70%训练集和30%测试集划分数据集，将595口井的结果进行加权平均，得出最终影响因素排名如表2所示。

表2 样本井钻井成本影响因素Top10及影响程度（不区分时空）

在得到影响因素及权重排名后，就可以针对影响因素进行基于机器学习的页岩气钻井成本动态建模，选择排名前10 的影响因素及相应权重作为参数进行建模。

2 页岩气钻井成本动态建模

在对页岩气钻井成本进行动态建模时，传统的单个机器学习模型如神经网络、随机森林、岭回归等模型都无法达到较好的解释和预测结果。主要原因有以下三点：第一，数据标准无法统一。如前文所述，影响页岩气钻井成本的因素主要有工程工艺、时序数据、空间数据三类，使用单一机器学习模型时，由于时空数据的异质性，线性和非线性数据叠加势必导致模型不能输出很好的结果。第二，多重共线性问题。页岩气钻井成本的影响因素中，很多因素之间都存在精确相关关系或高度相关关系而使模型失真，导致模型不稳定，使得某些特征的权重不准确。第三，模型过拟合问题。选择单一机器学习模型，当训练过程中整个数据集被遍历（epoch）的次数较大时，在模型收敛速度提升的同时，由于监督过度严格会带来模型过拟合风险，影响模型的泛化应用能力。为了尽量解决上述问题，笔者创造性的将数据按照时间和空间维度划分成两个子数据集，分别建立LSTM模型和SVM模型进行训练，最后利用Stacking方法进行模型融合。一定程度上提高了模型的预测精度并使模型具备良好的可解释性，也保证了模型的泛化能力。

2.1 基于时序数据的LSTM模型

长短期记忆网络（Long Short-Term Memory，LSTM）模型是一种递归神经网络（RNN）的变体，专注于处理和预测时序数据。LSTM 模型通过具备遗忘门、输入门和输出门的机制，能够有效地捕捉到时序数据中的长期依赖关系，特别擅长处理具有时间序列结构的数据，因此非常适合用于分析时序数据对页岩气钻井成本的影响。设计输入层、隐藏层和输出层三层结构，通过调整隐藏层的神经元数量、堆叠多层LSTM 等方式来保证模型性能。LSTM 模型原理图如图3所示。

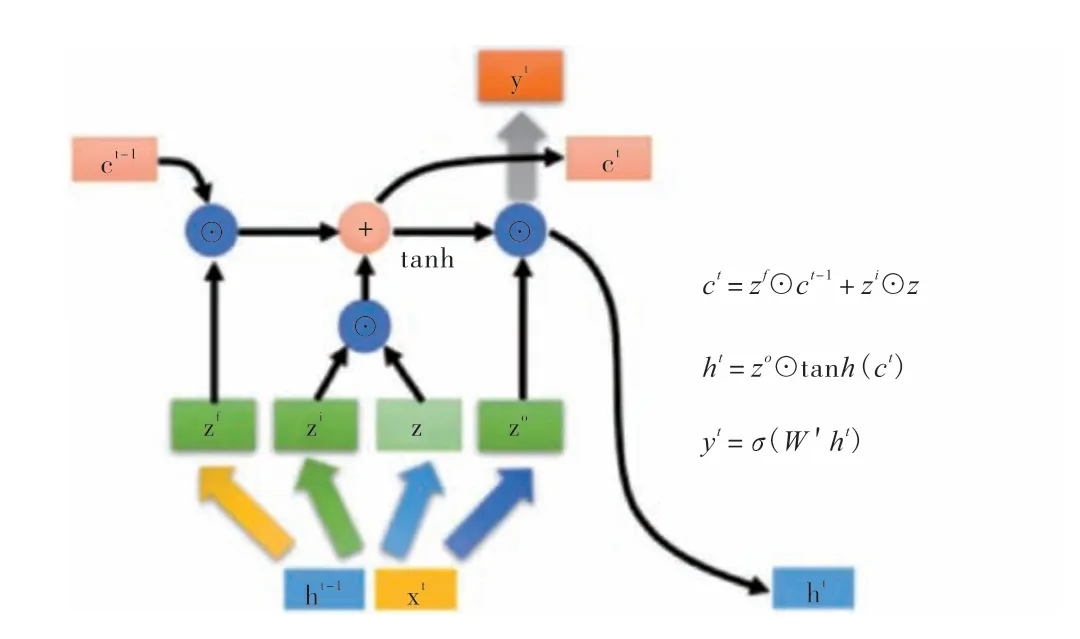
图3 长短期记忆网络（LSTM）模型原理图

将时序数据集按时间顺序进行排序，将数据集的70%划分为训练集，30%划分为测试集。训练过程选择均方误差损失函数和随机梯度下降法。模型输出结果如图4所示。

图4 LSTM模型输出结果图

2.2 基于空间数据的SVM模型

支持向量机（Support Vector Machine，SVM）模型是一种监督学习方法，广泛应用于分类和回归问题，能够处理具有多维特征的空间数据，通过构建超平面来实现对数据的分类或回归预测。SVM 模型建模时，需要选择合适的核函数，以将数据映射到高维空间中。通过使用SVM 模型，能够利用地理空间特征，对成本空间维度的分析。SVM 模型回归原理图如图5所示。

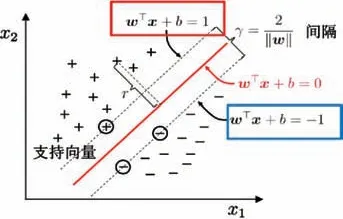
图5 SVM模型回归原理图

将空间数据按照井口序号进行归类，将数据集的70%划分为训练集，30%划分为测试集。在训练过程中，研究选择径向基函数（RBF）作为核函数，通过最小化分类误差求解最优超平面。采用Python 语言中的Scikit-learn 机器学习库实现输入空间数据集，输出模型结果。模型输出结果如图6所示。

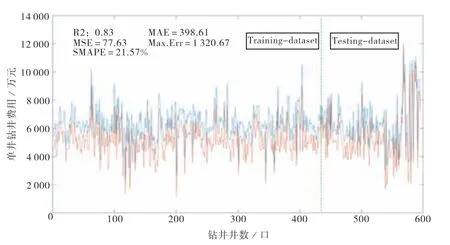
图6 SVM模型输出结果图

2.3 模型参数调整

在建立LSTM和SVM模型时，选择默认值作为初始参数。故建模后要通过合理地调整模型参数，提高模型的性能和预测准确性。采用网格搜索（Grid Search）对模型进行调参，网格搜索会在预先设定的参数组合范围内进行搜索和交叉验证，以找到最佳的参数组合。例如，通过定义参数网格，可以尝试不同的学习率、惩罚因子等参数组合，选择效果最好的参数组合。但多次调参后发现对于模型性能提升有限，因此，选择对LSTM模型和SVM模型进行融合。

3 模型融合与效果验证

3.1 模型之间的融合策略和原理

模型融合的策略是指将不同的模型结合起来，以提高预测准确性和稳定性。模型融合的原理在于利用不同模型之间的差异性和优势，整合多个模型的预测结果，达到更稳定、更准确的预测效果。模型融合能够提高模型的鲁棒性，减小预测误差，从而提供更可靠的成本预测和分析结果。需根据实际情况选择合适的融合策略，并根据模型的性能、数据的特点和任务需求进行调优和改进。

模型融合可以通过多种方式进行，常见的融合策略有平均法（Averaging）：通过将不同模型的预测结果进行平均，可以得到最终的融合结果。平均法可以有效地减少单个模型的偏差和方差，提高整体预测的准确性。堆叠法（Stacking）：首先使用多个不同的基础模型对数据进行预测，然后将这些基础模型的预测结果作为新特征输入到次级模型中，从而生成最终的融合结果。堆叠法能够利用不同模型的优点，进一步提高整体的预测能力。投票法（Voting）：通过多个模型对数据进行预测，并根据多数投票原则确定最终的预测结果。投票法适用于多个模型存在差异性，而不能确定单一最优模型的情况。笔者选择Stacking方法进行模型融合。

3.2 基于Stacking方法的模型融合

基于堆叠方法的模型融合是一种广泛应用的模型融合策略，通过将多个基础模型的预测结果作为新特征输入到次级模型中，生成最终的融合结果。首先将不区分时空的完整数据集进行重新划分，70%数据划分为训练集，用于训练次级模型，30%的数据划分为测试集，用于最终的预测和评估。然后将LSTM和SVM两个基础模型的预测结果作为新特征输入到次级模型中，与原始特征一起进行训练。通过多次对比尝试，最终选择XGBoost模型作为次级模型进行训练，以获得最佳融合效果。

3.3 模型效果验证

在得到次级模型的输出结果之后，对模型的效果和性能进行验证，交叉验证是一种常用的验证方法，可以避免由于单次训练集和测试集的划分带来的偶然性。常见的交叉验证方法包括K 折交叉验证和留一交叉验证。在K 折交叉验证中，将数据集分成K个子集，每次使用K-1个子集作为训练集，剩下的1个子集作为验证集。然后重复K次，最终得到K个模型的性能指标。最终得到融合后模型的确定系数R2 为0.96，均方误差（Mean Squared Error，MSE）为126.57，平均绝对误差（Mean Absolute Error，MAE）为110.04，最大误差（Max.Err）为656.30，对称平均绝对百分比误差（SMAPE）为14.38%，可以认为模型具有很好的效果。具体模型效果如图7所示。

图7 基于stacking方法的融合模型输出结果图

3.4 模型结果与优化建议

结合上述模型，通过对样本的595口井做了数据分析，经分析发现，钻井成本中压裂段数、井深和平台井数是相对较重要的影响因素。这些因素的不同取值将直接影响到钻井的成本和效率。可见建立的动态模型能够较好地为页岩气钻井成本的控制和优化提供决策依据，具备较高的应用价值。在决策钻井方案时，需要综合考虑油井的产能、地层情况、资源利用率、投资回报率等多方面因素，以确保钻井过程既能提高油井产能，又能最大程度地控制成本。此外，地质条件复杂、学习效率明显不足，管理成本过高，宏观经济形势、劳动力成本效率等因素也制约着页岩气钻井成本的下降。除了考虑现有的因素，构建钻井成本时空大数据集时，还可以从更多维度考虑因素，以进一步提高模型预测效果。其中，经济因素和钻井实际情况是两个重要的方面。通过综合考虑这些因素，能够更好地预测未来的钻井成本，并为决策提供更精确的参考依据。

4 结束语

当前，大数据技术及人工智能技术迅猛发展，对于页岩气钻井成本的影响因素分析和优化策略研究愈发依赖于大量数据的处理和挖掘。传统的成本分析方法往往忽略了这些非直接因素和大数据的作用，导致成本优化策略的实际效果受到限制。因此，立足对页岩气钻井成本多种影响因素的大数据分析，寻求一种综合性强、能充分考虑各种影响因素的成本分析方法，对于实现页岩气钻井成本的优化具有重要价值。

采用多源数据进行综合分析，使钻井成本的动态变化能够得以更全面、准确地描述。其次，引入了GBDT（Gradient Boosting Decision Tree）模型进行影响因素的排序和分析，可以帮助决策者更好地了解各个因素对成本的影响程度，从而制定更有效的优化策略。此外，使用LSTM模型和SVM模型分别对时间和空间数据进行建模，使成本预测更加可靠和准确。最后，通过Stacking 方法对模型进行融合应用，进一步提高了模型的预测能力和泛化能力，有效地应对了时空异质性的挑战。本次研究的主要贡献如下：①系统地收集并分析了页岩气钻井成本的直接和非直接影响因素，拓宽了研究视角；②分析了各影响因素之间的关系，为钻井成本优化提供了更深入的洞察；③通过深入挖掘各种影响因素、建立各类模型，并进行融合优化，实现了大数据驱动的页岩气钻井成本动态模型构建，可以为页岩气钻井成本的控制和优化提供决策依据，并为大数据驱动决策支撑的研究方向提供有益的启示。