包含Euler函数的一个三元变系数不定方程的正整数解
2024-01-13王丽张四保杨振志
王丽,张四保,杨振志
(1.喀什大学 数学与统计学院,新疆 喀什844000;2.喀什大学 现代数学及其应用研究中心,新疆 喀什 844000;3. 新疆昆玉城市建设投资运营集团有限责任公司,新疆 昆玉 848116)
令φ(n)是一正整数,φ(n)为Euler函数。Euler函数φ(n)是数论研究中的一个重要函数[1],其有着广泛的应用。关于Euler函数φ(n)的性质以及Euler函数方程的研究也吸引了众多学者的研究兴趣。如文献[2-9]分别讨论了包含Euler函数φ(n)的形如φ(xy)=m(φ(x)+φ(y))的二元定系数不定方程,当m=3,4,6,7,8,9,11,12,20时所对应方程的可解性;关于包含Euler函数φ(n)的形如φ(xyz)=m(φ(x)+φ(y)+φ(z))的三元定系数不定方程的可解性研究内容丰富,如文献[10-14]分别讨论了当m=2,3,4,5,6时所对应的方程的可解性,给出了相应方程的所有正整数解;关于包含Euler函数φ(n)的形如φ(xyz)=k1φ(x)+k2φ(y)+k3φ(z)的三元变系数不定方程的可解性也引起不少学者的研究兴趣,如文献[15]讨论了方程φ(xyz)=φ(x)+2φ(y)+3φ(z))的可解性,并给出了其所有正整数解;文献[16]讨论了方程φ(xyz)=2φ(x)+3φ(y)+4φ(z)的可解性。针对包含Euler函数φ(n)的形如φ(xyz)=k1φ(x)+k2φ(y)+k3φ(z)的三元变系数不定方程的可解性问题,本文将在之前研究的基础上,讨论当k1=1,k2=3,k3=4时方程的可解性,即讨论方程
φ(xyz)=φ(x)+3φ(y)+4φ(z)
(1)
的可解性,并给出其所有的正整数解。
1 相关引理
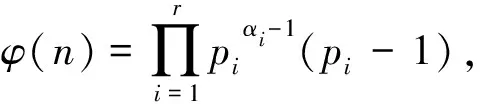
引理2[17]对任意的正整数m与n,有
显然,若gcd(m,n)=1,则有φ(mn)=φ(m)φ(n)。
引理3[18]当≥2时,有φ(n) 定理1 不定方程(1)有正整数解(x,y,z)= (6,6,1),(6,3,2),(3,6,2),(11,3,1),(11,3,2),(11,4,1),(11,6,1),(22,3,1),(3,4,4),(4,3,4),(4,4,3),(5,5,1),(5,10,1),(5,5,2),(10,5,1),(3,14,2),(4,14,1),(4,18,1),(4,7,2),(4,9,2),(6,14,1),(6,7,2),(3,3,5),(3,3,8),(3,3,10),(3,6,5),(6,3,5),(5,16,1),(5,24,1),(8,15,1),(3,11,4),(4,11,3),共有32组。 证明由引理2知 由引理3可得 φ(x)[φ(y)φ(z)-1]≤3φ(y)+4φ(z)。 (2) 由于φ(y)φ(z)>0,则可按φ(y)φ(z)的取值分以下3种情况讨论。 情况1 当φ(y)φ(z)=1 此时有φ(y)=φ(z)=1,则y=z=1,2。由方程(1)可得φ(xyz)=7+φ(x)。由引理3得φ(x)=1,则x=1,2,且φ(xyz)=8,则xyz=15,16,20,24, 30。而此时x,y,z的乘积xyz≠15,16,20,24,30,则此时方程(1)无整数解。 情况2 当2≤φ(y)φ(z)≤8 此时由式(2)可得 (3) 由于(φ(y)-1)(φ(z)-1)≥0,可得 φ(y)+φ(z)≤φ(y)φ(z)+1, 将其代入式(3),得 (4) 情况2.1当φ(y)φ(z)=2 此时有φ(y)=1,φ(z)=2或φ(y)=2,φ(z)=1。当φ(y)=1,φ(z)=2时,有y=1,2,z=3,4,6。当φ(y)=2,φ(z)=1时,有y=3,4,6,z=1,2。又由式(4),此时则有φ(x)=1,2,4,6,8,10。 当φ(x)=1时,有φ(xyz)。当φ(y)=1,φ(z)=2时,有φ(xyz)=12,则xyz=13,21,26,28,36,42。经计算,此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=11,由引理3可得此式不成立,此时方程(1)无整数解。 当φ(x)=2时,有x=3,4,6。当φ(y)=1,φ(z)=2时,有φ(xyz)=13,由引理3知此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=12,则xyz=13,21,26,28,36,42。经计算,此时方程(1)有整数解(x,y,z)=(6,6,1),(6,3,2),(3,6,2)。 当φ(x)=4时,有x=5,8,10,12。当φ(y)=1,φ(z)=2时,有φ(xyz)=15,由引理3可得此式不成立,此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=14。由于14是非Euler商数,所以此时方程(1)无整数解。 当φ(x)=6时,有x=7,9,14,18。当φ(y)=1,φ(z)=2时,有φ(xyz)=17,由引理3可得此式不成立,此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=16,则xyz=17,32,34,40,48,60。经计算,此时方程(1)无整数解。 当φ(x)=8时,有x=15,16,20,24,30。当φ(y)=1,φ(z)=2时,有φ(xyz)=19,由引理3可得此式不成立,此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=18,则xyz=19,27,38,54。经计算,此时方程(1)无整数解。 当φ(x)=10时,有x=11,22。当φ(y)=1,φ(z)=2时,有φ(xyz)=21,由引理3可得此式不成立,此时方程(1)无整数解。当φ(y)=2,φ(z)=1时,有φ(xyz)=20,,则xyz=25,33,44,50,66。经计算,此时方程(1)有整数解(x,y,z)=(11,3,1),(11,3,2,),(11,4,1),(11,6,1),(22,3,1)。 情况2.2 当φ(y)φ(z)=4 此时有φ(y)=1,φ(z)=4或φ(y)=2,φ(z)=2或φ(y)=4,φ(z)=1。当φ(y)=1,φ(z)=4时,有y=1,2,z=5,8,10,12。当φ(y)=2,φ(z)=2时,有y=z=3,4,6。当φ(y)=4,φ(z)=1时,有y=5,8,10,12,z=1,2。此时,由式(4)有φ(x)≤6,则φ(x)=1,2,4,6。 当φ(x)=1时,有x=1,2。若φ(y)=1,φ(z)=4,有φ(xyz)=20,则xyz=25,33,44,50,66。经计算,此时方程(1)无整数解。若φ(y)=2,φ(z)=2,有φ(xyz)=15。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=4,φ(z)=1,有φ(xyz)=17,。由引理3可得此式不成立,此时方程(1)无整数解。 当φ(x)=2时,有x=3,4,6。若φ(y)=1,φ(z)=4,有φ(xyz)=21。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=2,φ(z)=2,有φ(xyz)=16,则xyz=17,32,34,40,48,60。经计算,此时方程(1)有整数解(x,y,z)=(3,4,4),(4,3,4),(4,4,3)。若φ(y)=4,φ(z)=1,有φ(xyz)=18,则xyz=19,27,38,54。经计算,此时方程(1)无整数解。 当φ(x)=4时,有x=5,8,10,12。若φ(y)=1,φ(z)=4,有φ(xyz)=23。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=2,φ(z)=2,有φ(xyz)=18,则xyz=19,27,38,54。经计算,此时方程(1)无整数解。若φ(y)=4,φ(z)=1,有φ(xyz)=20。则xyz=25,33,44,50,66。经计算,此时方程(1)有整数解(x,y,z)=(5,5,1),(5,10,1),(5,5,2),(10,5,1)。 当φ(x)=6时,有x=7,9,14,18。若φ(y)=1,φ(z)=4,有φ(xyz)=25。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=2,φ(z)=2,有φ(xyz)=20,则xyz=25,33,44,50,66。经计算,此时方程(1)无整数解。若φ(y)=4,φ(z)=1,有φ(xyz)=22,则xyz=23,46。经计算,此时方程(1)无整数解。 情况2.3当φ(y)φ(z)=6 此时有φ(y)=1,φ(z)=6或φ(y)=6,φ(z)=1。当φ(y)=1,φ(z)=6时,有y=1,2,z=7,9,14, 18。当φ(y)=6,φ(z)=1时,有y=7,9,1,4,18,x=1,2。此时由式(4)有φ(x)=1,2,4。 当φ(x)=1时,有x=1,2。若φ(y)=1,φ(z)=6,有φ(xyz)=28,则xyz=29,58。经计算,此时方程(1)无整数解。若φ(y)=6,φ(z)=1,有φ(xyz)=23。由引理3可得此式不成立,此时方程(1)无整数解。 当φ(x)=2时,有x=3,4,6。若φ(y)=1,φ(z)=6,有φ(xyz)=29。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=6,φ(z)=1,有φ(xyz)=24,有xyz=35,39,45, 52,56,70,72,78,84,90。经计算,此时方程(1)有整数解(x,y,z)=(3,14,2),(4,14,1),(4,18,1),(4,7,2),(4,9,2),(6,14,1),(6,7,2)。 当φ(x)=4时,有x=5,8,10,12。若φ(y)=1,φ(z)=6,有φ(xyz)=31。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=6,φ(z)=1,有φ(xyz)=26。由于26是非Euler商数,φ(xyz)=26无解,所以此时方程(1)无整数解。 情况2.4当φ(y)φ(z)=8 此时有φ(y)=1,φ(z)=8或φ(y)=2,φ(z)=4或φ(y)=4,φ(z)=2或φ(y)=8,φ(z)=1。当φ(y)=1,φ(z)=8时,有y=1,2,z=15,16,20, 24,30。当φ(y)=2,φ(z)=4时,有y=3,4,6,z=5,8,10,12。当φ(y)=4,φ(z)=2时,有y= 5,8,10,12,z=3,4,6。当φ(y)=8,φ(z)=1时,有y=15,16,20,24,30,z=1,2。此时,由式(4)有φ(x)≤5,则φ(x)=1,2,4。 当φ(x)=1时,有x=1,2。若φ(y)=1,φ(z)=8,有φ(xyz)=36,则xyz=37,57,63,74, 76,108,114,126。经计算,此时方程(1)无整数解。若φ(y)=8,φ(z)=1,有φ(xyz)=29。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=2,φ(z)=4,有φ(xyz)=23。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=4,φ(z)=2,有φ(xyz)=21。由引理3可得此式不成立,此时方程(1)无整数解。 当φ(x)=2时,有x=3,4,6。若φ(y)=1,φ(z)=8,有φ(xyz)=37。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=8,φ(z)=1,有φ(xyz)=30,则xyz=31,62。经计算,此时方程(1)无整数解。若φ(y)=2,φ(z)=4,有φ(xyz)=24,有xyz=35,39,45,52,56,70,72,78 84,90。经计算,此时方程(1)有整数解(x,y,z)= (3,3,5),(3,3,8),(3,3,10),(3,6,5),(6,3,5)。若φ(y)=4,φ(z)=2,有φ(xyz)=22,则xyz= 23,46。经计算,此时方程(1)无整数解。 当φ(x)=4时,有x=5,8,10,12。若φ(y)=1,φ(z)=8,有φ(xyz)=39。由引理3可得此式不成立,此时方程(1)无整数解。若φ(y)=8,φ(z)=1,有φ(xyz)=32,则xyz=51,64,68,80,96,102,120。经计算,此时方程(1)有整数解(x,y,z)=(5,16,1),(5,24,1),(8,15,1)。若φ(y)=2,φ(z)=4,有φ(xyz)=26。由于26是非Euler商数,因而此时方程(1)无整数解。若φ(y)=4,φ(z)=2,有φ(xyz)=24,则xyz=35,39,45,52,56,70,72,78, 84,90。经计算,此时方程(1)无整数解。 情况3当φ(y)φ(z)≥10 此时,由式(4)可得,φ(x)=1,2,4。 情况3.1当φ(x)=1 此时,有 φ(xyz)=1+3φ(y)+4φ(z)= φ(x)φ(y)φ(z)=φ(y)φ(z), 则φ(y)φ(z)≤1+3φ(y)+4φ(z)<1+4[φ(y)+φ(z)],从而有 [φ(y)-4][φ(z)-4]<17, 因此可以分以下两种情况讨论。 1)当φ(y)=1时,有φ(z)≥10,则φ(xyz)=4+ 4φ(z),则x,y=1,2。 取(x,y)=(1,1)时,有φ(z)=4+4φ(z),显然此式不成立,此时方程(1)无整数解。 取(x,y)=(1,2)时,有φ(2z)=4+4φ(z)。当gcd(2,z)=1时,有φ(2z)=φ(z),则φ(2z)=4+ 4φ(z)无解,此时方程(1)无整数解;当gcd(2,z)=2时,有φ(2z)=2φ(z),则φ(2z)=4+ 4φ(z)无解,此时方程(1)无整数解。 取(x,y)= (2,1)时,此情况与取(x,y)=(1,2)相同,此时方程(1)无整数解。 取(x,y)=(2,2)时,有φ(4z)=4+4φ(z)。当gcd(4,z)=1时,有φ(4z)=2φ(z),则φ(4z)=4+ 4φ(z)无解,此时方程(1)无整数解;当gcd(4,z)=2,4时,有φ(4z)=4φ(z),则φ(4z)=4+4φ(z)无解,此时方程(1)无整数解。 2)当φ(y)≥2时,由方程(1)有φ(xyz)=1+ 3φ(y)+4φ(z),此时1+3φ(y)+4φ(z)显然是一个大于1的奇数,由引理3可得此时方程(1)无整数解。 情况3.2当φ(x)=2 此时,有 φ(xyz)=φ(x)+3φ(y)+4φ(z)=2+3φ(y)+ 4φ(z)≥φ(x)φ(y)φ(z)=2φ(y)φ(z), 即 φ(y)[2φ(z)-3]≤2+4φ(z), (5) 因此可以分以下6种情况讨论。 1)当φ(z)=1时,有φ(xyz)=6+3φ(y)。此时有x=3,4,6,z=1,2。 取(x,z)=(3,1)时,有φ(3y)=6+3φ(y)。当gcd(3,y)=1时,有φ(3y)=2φ(y),显然此时φ(3y)=6+3φ(y)无解,因而此时方程(1)无整数解。当gcd(3,y)=3时,有φ(3y)=3φ(y),显然此时φ(3y)=6+3φ(y)无解,因而此时方程(1)无整数解。 取(x,z)=(3,2)时,有φ(6y)=6+3φ(y)。当gcd(6,y)=1时,有φ(6y)=2φ(y),显然此时φ(6y)=6+3φ(y)无解,因而此时方程(1)无整数解。当gcd(6,y)=2时,有φ(6y)=4φ(y),此时φ(6y)=6+3φ(y)有解φ(y)=6。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。当gcd(6,y)=3时,有φ(6y)=3φ(y),显然此时φ(6y)=6+3φ(y)无解,因而此时方程(1)无整数解。当gcd(6,y)=6时,有φ(6y)=6φ(y),此时φ(6y)=6+3φ(y)有解φ(y)=2。结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。 取(x,z)=(4,1)时,有φ(4y)=6+3φ(y)。当gcd(4,y)=1时,有φ(4y)=2φ(y),显然此时φ(4y)=6+3φ(y)无解,因而此时方程(1)无整数解。当gcd(4,y)=2,4时,都有φ(4y)=4φ(y),此时φ(4y)=6+3φ(y)有解φ(y)=6。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。 取(x,z)=(4,2)时,有φ(8y)=6+3φ(y)。当gcd(8,y)=1时,有φ(8y)=4φ(y),此时φ(8y)= 6+3φ(y)有解φ(y)=6。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。当gcd(8,y)=2,4,8时,都有φ(8y)=8φ(y),此时φ(8y)=6+3φ(y)无解,则此时方程(1)无整数解。 取(x,z)=(6,1)时,有φ(6y)=6+3φ(y)。当gcd(6,y)=1时,有φ(6y)=2φ(y),显然此时φ(6y)=6+3φ(y)无解,此时方程(1)无整数解。当gcd(6,y)=2时,有φ(6y)=4φ(y),此时φ(6y)=6+3φ(y)有解φ(y)=6。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。当gcd(6,y)=3时,有φ(6y)=3φ(y),显然此时φ(6y)=6+3φ(y)无解,此时方程(1)无整数解。当gcd(6,y)=6时,有φ(6y)=6φ(y),此时φ(6y)= 6+3φ(y)有解φ(y)=2。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。 取(x,z)=(6,2)时,有φ(12y)=6+3φ(y)。当gcd(12,y)=1时,有φ(12y)=4φ(y),此时φ(12y)=6+3φ(y)有解φ(y)=6。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。当gcd(12,y)=2,4时,都有φ(12y)=8φ(y),此时φ(12y)=6+3φ(y)无解,此时方程(1)无整数解。当gcd(12,y)=3时,有φ(12y)=6φ(y),此时φ(12y)=6+3φ(y)有解φ(y)=2。此时结合φ(z)=1与φ(y)φ(z)≥10可知,此时方程(1)无整数解。当gcd(12,y)=6,12时,有φ(12y)=12φ(y),此时φ(12y)=6+3φ(y)无解,此时方程(1)无整数解。 2)当φ(z)=2时,有x=z=3,4,6。将φ(z)=2代入式(5)得φ(y)≤10。又φ(y)φ(z)≥10,可得φ(y)=6,8,10。当φ(y)= 6时,有y=7,9,14,18。此时有φ(xyz)=28,则xyz=29,58。经计算,此时方程(1)无整数解。当φ(y)=8时,有y=15,16,20,24,30。此时φ(xyz)=34。由于34是非Euler商数,则φ(xyz)= 34无解,则此时方程(1)无整数解。当φ(y)=10时,有y=11,22。此时φ(xyz)=40,则xyz=41, 55,75,82,88,100,110,132,150。经计算,此时方程(1)有整数解(x,y,z)=(3,11,4),(4,11,3)。 3)当φ(z)=4时,有x=3,4,6,z=5,8,10,12。将φ(z)=4代入式(5)有φ(y)≤4。又φ(y)φ(z)≥ 10,所以有φ(y)=4,则y=5,8,10,12。此时有φ(xyz)=22,则xyz=23,46。经计算,此时方程(1)无整数解。 4)当φ(z)=6时,有x=3,4,6,z=7,9,14,18。将φ(z)=6代入式(5)有φ(y)≤2。又φ(y)φ(z)≥ 10,所以有φ(y)=2,则y=3,4,6,此时φ(xyz)= 32,则xyz=51,64,68,80,96,102,120。经计算,此时方程(1)无整数解。 5)当φ(z)=8时,有x=3,4,6,z=15,16,20, 24,30。将φ(z)=8代入式(5)有φ(y)≤2。又φ(y)φ(z)≥10,所以有φ(y)=2,y=3,4,6。此时φ(xyz)=40,则xyz=41,55,75,82,88,100,110,132,150。经计算,此时方程(1)无整数解。 6)当φ(z)≥10时,由式(5)可得 即φ(y)<3,所以φ(y)=1,2。当φ(y)=1时,由φ(x)+3φ(y)+4φ(z)≥φ(x)φ(y)φ(z)得2φ(z)≤ 5+4φ(z),这不可能成立,此时方程(1)无整数解。当φ(y)=2时,由φ(x)+3φ(y)+4φ(z)≥φ(x)φ(y)φ(z)得4φ(z)≤8+4φ(z)。经计算,此时方程(1)无整数解。 情况3.3当φ(x)=4 此时,有 φ(xyz)=φ(x)+3φ(y)+4φ(z)=4+3φ(y)+ 4φ(z)≥φ(x)φ(y)φ(z)=4φ(y)φ(z), 即 4φ(z)[φ(y)-1]≤4+3φ(y), (6) 因此可以分以下4种情况讨论。 当φ(y)=1时,有φ(xyz)=φ(x)+3φ(y)+ 4φ(z)=7+4φ(z),显然此式不成立,此时方程(1)无整数解。 当φ(y)=2时,代入式(6)有φ(z)≤2。又φ(y)φ(z)≥10,此时方程(1)无整数解。 当φ(y)=4,6,8时,代入式(6)有φ(z)≤1。又φ(y)φ(z)≥10,此时方程(1)无整数解。 当φ(y)≥10时,由式(6)可得 结合以上3种情况的讨论,可得定理1。 针对包含Euler函数φ(n)的形如φ(xyz)=k1φ(x)+k2φ(y)+k3φ(z))的三元变系数不定方程的可解性问题,讨论了三元变系数不定方程φ(xyz)=φ(x)+3φ(y)+4φ(z)的可解性问题,通过分类讨论以及相关内容,采用分析筛选获得该不定方程的所有32组正整数解。2 主要定理及证明
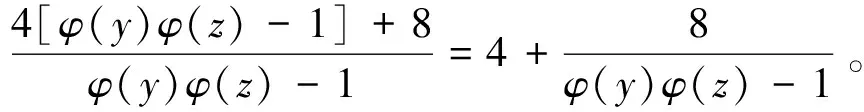

3 结束语
