基于自抗扰控制的车用异步电机参数辨识
2024-01-13张世龙李军伟李连强王东
张世龙,李军伟,李连强,王东
(1.山东理工大学 交通与车辆工程学院,山东 淄博 255049;2.一汽解放青岛汽车有限公司,山东 青岛 266200;3. 北京乾勤科技发展有限公司,北京 100084)
随着变频调速技术的发展,交流异步电机控制技术也更加成熟,控制更加方便,控制精度越来越高,因此交流异步电机的应用场合也愈加广阔。通常采用基于磁场定向的矢量控制方法实现对交流异步电机的高性能控制,这种控制方法需要较为准确的电机参数,如转子时间常数等[1]。由于转子时间常数对磁链和转矩的解耦具有较大影响,因此,需要一种能够在线辨识转子时间常数的辨识方案,确保交流异步电机在不同工况下的控制性能。
电机参数辨识有多种方法,包含模型参考自适应算法、最小二乘法及扩展卡尔曼滤波法等[2]。吴锦宇[3]利用模型参考自适应算法,使用基于无功功率模型对转子时间常数进行辨识,得到了准确的辨识结果。王晓晨[4]利用ICS算法和MRAS相结合的方法对电机的交直轴电感进行辨识,得到了准确的交直轴电感。
为避免转子时间常数变化对基于转子磁场的矢量控制系统的影响,本文以定子侧的电压、电流信号以及转子速度作为输入量,采用基于MRAS和GA-ADRC结合的方法,实现对转子时间常数的在线辨识并通过仿真实验验证该方法的可行性。
1 转子时间常数辨识公式推导
本文使用模型参考自适应算法对转子时间常数进行辨识,利用基于转子磁链的电流模型设计模型参考自适应算法的可调模型,如式(1)所示。根据转子磁链的电压模型设计模型参考自适应算法的参考模型,如式(2)所示。
(1)
(2)
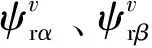
根据Popov超稳定原理设计自适应机构,如式(3)所示。
(3)
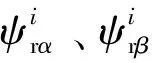

图1 转子时间常数辨识框图
基于转子磁链的电压模型含有纯积分,会出现积分饱和问题[5],导致出现直流偏置的现象,使得转子时间常数辨识不准确。同时,定子电阻随电机温度的变化而变化,导致基于转子磁链的电压模型输出的转子磁链不准确[6],无法作为参考模型的输出。因此,需要对辨识模型进行优化。
2 基于MRAS的转子时间常数辨识模型优化
本文提出基于MRAS和GA-ADRC相结合的方法对转子时间常数进行辨识,并将其应用在交流异步电机矢量控制系统中,其整体框架如图2所示。
图2中,在交流异步电机矢量控制系统的基础上添加参数辨识模型,辨识模型输出的转子时间常数会反馈到磁链观测器,实现了励磁与转矩的解耦[7]。
基于MRAS和GA-ADRC的转子时间常数辨识框图如图3所示。图3中,通过转子磁链的电压和电流模型对转子时间常数进行辨识,通过定子磁链的电压和电流模型对定子电阻进行辨识[8]。将定子电阻辨识值反馈至转子磁链的电流模型,以消除定子电阻对参考模型的影响。为提高转子时间常数辨识结果的准确性,本文基于GA-ADRC对自适应机构的调节参数进行优化。
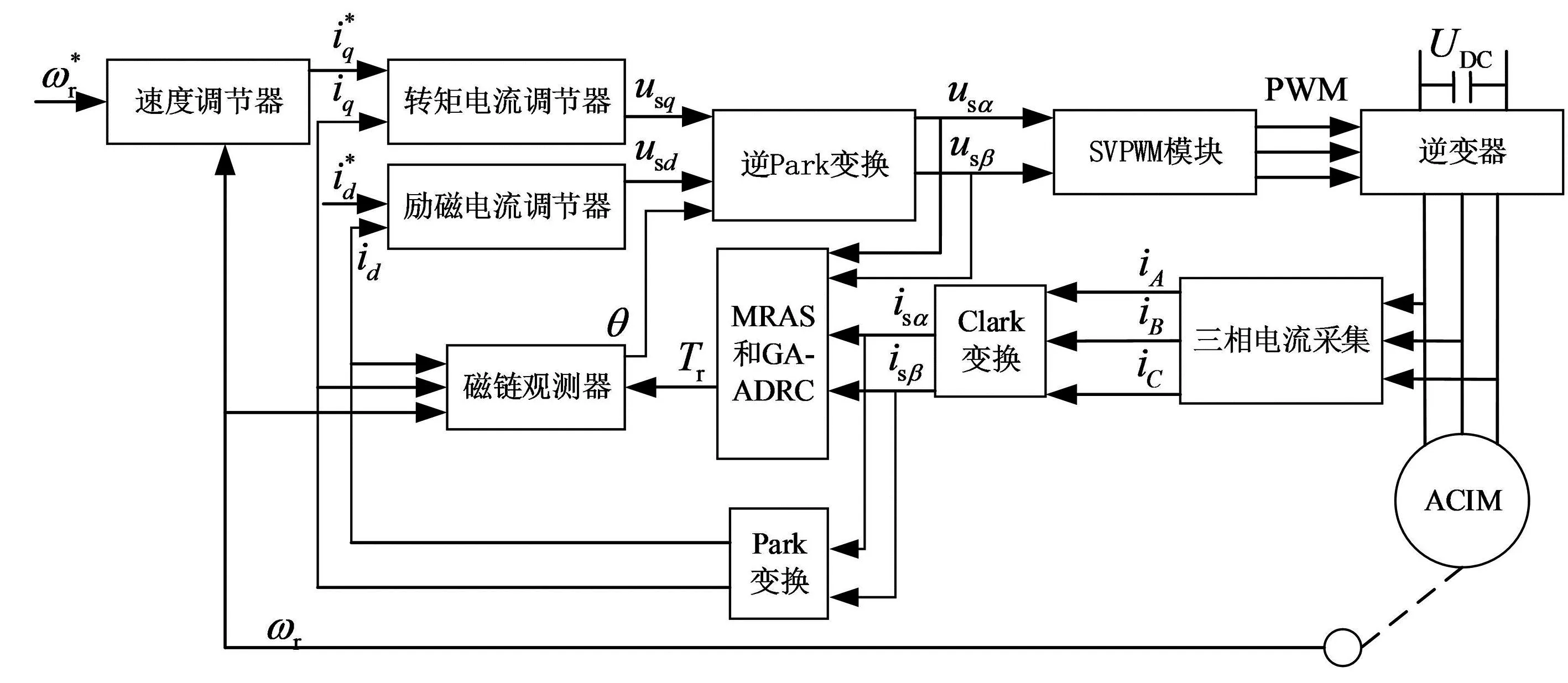
图2 基于MRAS和GA-ADRC参数辨识的交流异步电机矢量控制框图

图3 基于MRAS和GA-ADRC的转子时间常数辨识框图
2.1 基于MRAS的转子时间常数优化辨识
由式(2)可知,基于转子磁链的电压模型含有纯积分,会出现积分饱和问题,导致辨识效果不理想,本文将电压模型与低通滤波器相结合,以消除积分饱和对转子磁链电压模型的影响,优化后的转子时间常数辨识数学模型如式(4)和式(5)所示。
(4)
(5)
式(5)中ωcl为截止频率。为消除低通滤波器引起的相位偏差,对截止频率进行实时调整。当转子角速度低于或等于200 rad/s时,截止频率设置为30 rad/s;当转子角速度高于200 rad/s时,截止频率设置为0.15倍的转子角速度。
为避免定子电阻变化对转子时间常数辨识造成影响,本文对定子电阻进行辨识,并将定子电阻辨识值作为参考模型的输入量,传给转子时间常数辨识模型,以提高转子时间常数辨识的准确性。
本文使用定子磁链的电压模型对模型参考自适应算法的可调模型进行设计,如式(6)所示。使用定子磁链的电流模型对模型参考自适应算法的参考模型进行设计,如式(7)所示。
(6)
(7)
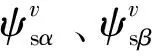
根据Popov超稳定性原理设计自适应机构如式(8)所示。
(8)
式中kp1、ki1分别为定子电阻辨识的增益参数。
2.2 GA-ADRC控制器设计
基于GA-ADRC的自适应机构框图如图4所示。遗传算法基本思想是通过对运行参数初始化,获得第一代种群个体,然后通过选择、交叉以及变异操作,求取个体适应度值,根据适应度值对个体进行评价,得到优秀的个体[9]。遗传算法的核心是适应度函数的选取和设计。本文选取的适应度函数由超调量、调整时间和转子磁链误差三部分组成,如式(9)所示。
f=0.1ts+0.8δ+0.1Mp
(9)
式中:ts为调整时间,δ为转子磁链误差,Mp为超调量。
自抗扰控制包含跟踪微分器、扩张状态观测器和线性状态误差反馈控制率三部分[10]。跟踪微分器和线性状态误差反馈控制率可以控制被控量快速达到稳定值且无超调。扩张状态观测器可以将被控量建模所涉及的动态未知部分和外部带来的扰动干扰归纳为对整体的总干扰,并对其进行估计和补偿。
本文以转子磁链控制为目标对ADRC控制器进行设计。转子磁链在d_q坐标系下的数学模型如式(10)所示。
(10)
式中:ψr为转子磁链,isd为励磁电流,ω1为同步旋转电角速度。
1)跟踪微分器。跟踪微分器以转子磁链作为输入信号,输出信号为θ(k)和ψr(k), 其中θ(k)为跟踪输入信号,ψr(k)为θ(k)的微分。
对电机控制系统进行离散化处理得
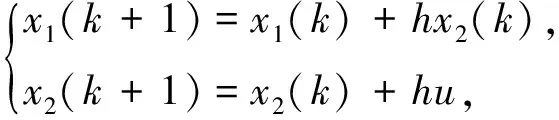
(11)
式中u=fst(x1,x2,r,h)为快速控制最优综合函数。将u=fst(x1,x2,r,h)代入式(11),化简得快速离散跟踪微分器如式(12)所示。
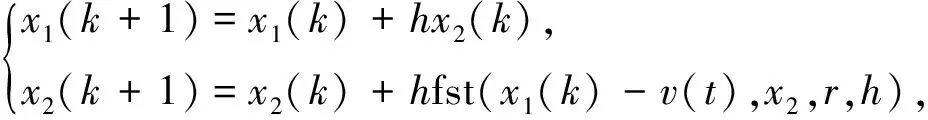
(12)
式中:h为设定采样周期,v(t)为输入信号。
将转子磁链代入式(12)并化简可得跟踪微分器方程
(13)
式中e0为转子磁链的偏差。
2)扩张状态观测器。d_q坐标系中,转子磁链数学模型中的 “扰动部分”包含互感与转矩电流的耦合项,以及一些受工况变化的定转子电阻等电机参数,将其归纳为扰动项,利用扩张状态观测器进行估计和补偿。
对于电机非线性控制系统,可得如下观测器公式:
(14)
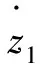
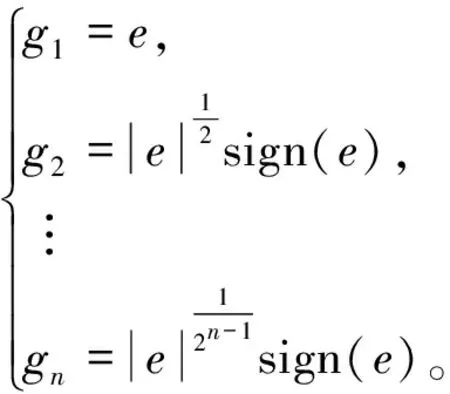
(15)
由式(13)—式(15)可得电机控制系统的扩张状态观测器方程为
(16)
式中:u(k)表示输入量,β1、β2以及β3为ESO的控制参数,ψr(k)为电机转子磁链,b为增益系数。
3)线性误差反馈控制率。误差反馈系统包含线性和非线性两种反馈控制策略,本文采用线性反馈控制策略,误差反馈率方程为
u(k)=α1(θ(k)-z1(k))+α2(ω(k)-z2(k)),
(17)
式中α1和α2为控制参数,该参数用来调节系统输出。
通过遗传算法整定ADRC参数步骤如下:
1)对运行参数进行初始化设置,包括进化迭代次数、种群规模、交叉概率、变异概率以及节点信息。选取ADRC控制中的β1、β2以及β3作为遗传算法中的种群个体。
2)通过初始化种群获得第一代个体,然后将需要整定的ADRC控制器参数赋值,运行交流异步电机参数辨识控制系统。
3)在主循环中运行选择、交叉和变异操作,计算种群和个体的适应度,对种群进行优胜劣汰,然后更新种群和个体的适应度值。交叉操作和变异操作的计算公式如式(18)、式(19)所示。
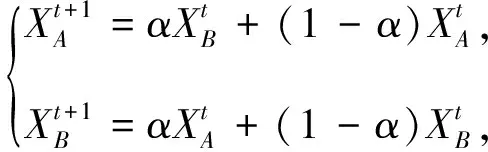
(18)
式中:α为一定范围内的随机数,XA、XB为种群的两个个体。

(19)

4)运行至设定的最大迭代次数为止,此时输出的ADRC参数即为经过遗传算法整定后的优化参数。
遗传算法优化ADRC参数流程如图5所示。图5中,通过浮点数编码对种群进行初始化设置,然后将种群个体赋值给电机矢量控制系统的自适应机构。通过sim函数调用交流异步电机控制系统,模型文件运行完毕后会得到转子磁链的大小、调整时间以及超调量的值。利用适应度函数计算每一次迭代时的适应度值并进行记录,由此得到个体极值和种群在全局下的极值。对上一代优化得到的优秀个体再次进行选择、交叉和变异操作,将得到的新的个体值带入到式(9)中计算种群个体适应度值,将此值与上一代最优值进行比较,根据适应度值将不合适的种群淘汰。在迭代次数内多次运行电机矢量控制系统,将每次得到的全局最优值进行比较,当达到最大迭代次数时,输出最终的β1、β2和β3。
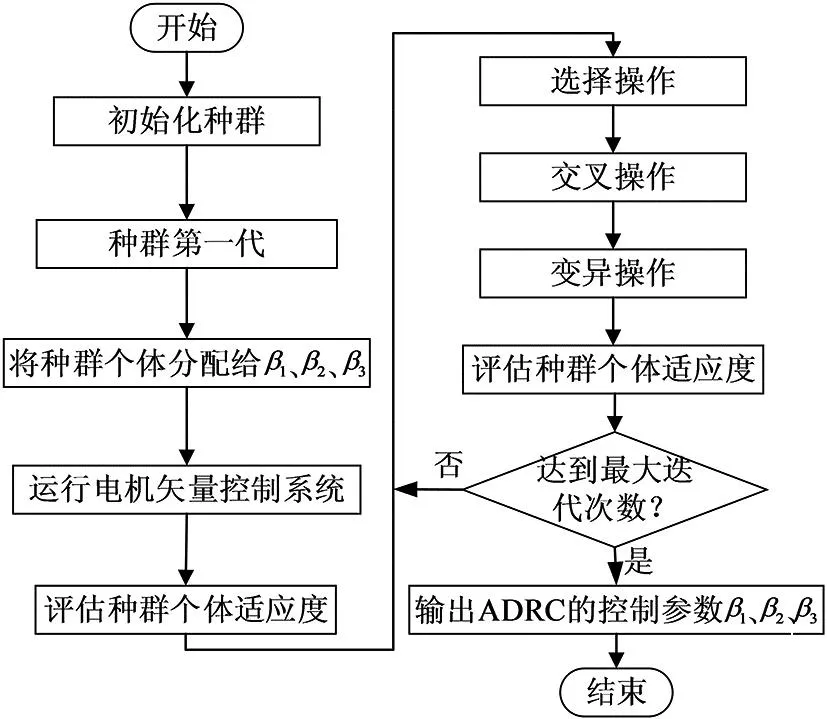
图5 遗传算法优化ADRC参数流程图
3 仿真分析
利用MATLAB/Simulink搭建交流异步电机参数辨识矢量控制系统,利用仿真实验验证矢量控制系统和转子时间常数辨识模型的有效性[11],相关实验参数见表1。

表1 交流感应电机仿真性能参数
本文采用MRAS和GA-ADRC相结合的方法,对转子时间常数进行在线辨识,通过对比试验,观察转子时间常数辨识在电机控制系统中所起的作用。仿真工况设置如下:设定运行转速1 000 r/min,分别改变转子电阻和定子电阻,其中转子电阻在0~<0.3 s时保持0.37 Ω不变,在0.3 s时由0.37 Ω变为0.16 Ω,同时给定10 N·m的负载,观察转子时间常数辨识值是否跟随变化;定子电阻在0~<0.5 s时保持初始值0.5 Ω不变,在0.5 s时由0.5 Ω增大为0.9 Ω。仿真实验结果如图6—图9所示。
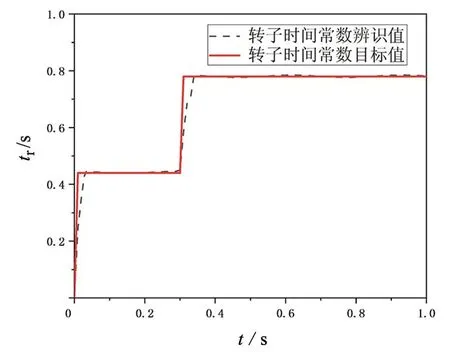
图6 转子时间常数的响应曲线
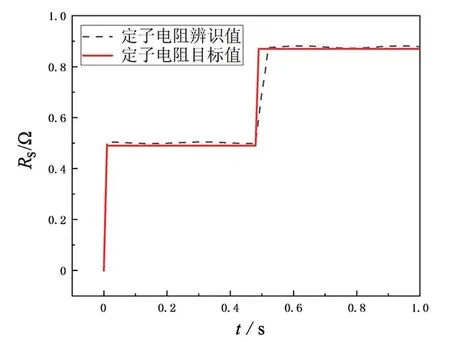
图7 定子电阻的响应曲线
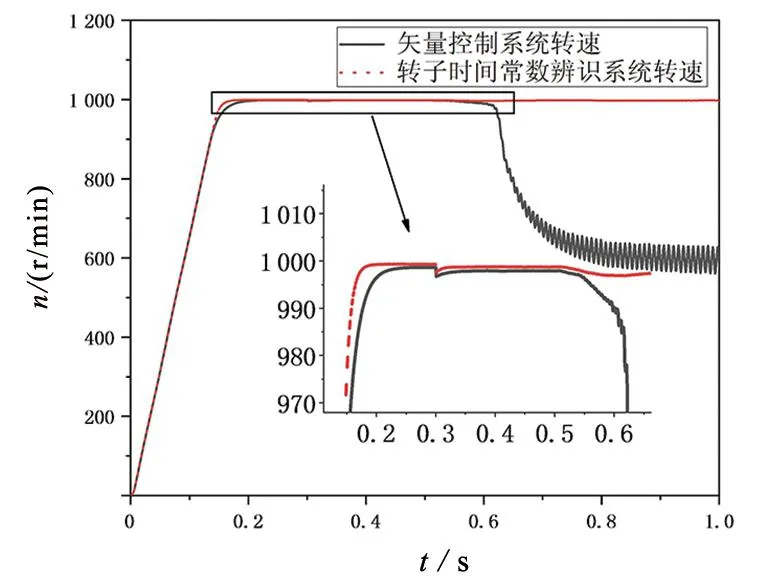
图8 转速响应的对比曲线
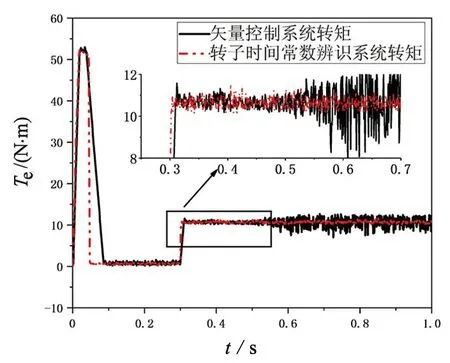
图9 转矩响应的对比曲线
图6为转子时间常数的响应曲线,由图6可知,在0~<0.3 s内转子电阻保持0.37 Ω不变,在0.3 s时转子电阻由0.37 Ω变为0.16 Ω,转子时间常数辨识值跟随目标值,辨识无错误;在0.5 s时定子电阻由0.5 Ω增大为0.9 Ω,转子磁链电压模型中的定子电阻随定子电阻辨识模型发生了改变,转子时间常数辨识结果正常,证明该方法可以有效辨识转子时间常数的变化。
图7为定子电阻的响应曲线,由图7可知,在0~<0.5 s内定子电阻保持0.5 Ω不变,在0.5 s时定子电阻由0.5 Ω增大为0.9 Ω,定子电阻辨识值跟随目标值,证明该方法可以有效辨识定子电阻的变化。
图8为转子电阻在0.3 s时由0.37 Ω变为0.16 Ω和定子电阻在0.5 s时由0.5 Ω增大为0.9 Ω时,矢量控制系统和参数辨识系统的转速响应。由图8可知,参数辨识系统的转速到达稳态时间相比于矢量控制系统提高了约10 ms,在0.3 s时,施加10 N·m的负载,辨识系统下的转速约下降2 r/min,矢量控制系统下的转速约下降4 r/min,辨识系统相比于矢量控制系统抗干扰性更好。在0.5 s时,定子电阻由0.5 Ω增大为0.9 Ω,矢量控制系统下的转速由于励磁和转矩无法正常解耦,转速开始缓慢降低,在0.62 s时转速突然下降和震荡,响应效果变差。两者对比可知,辨识系统相比于矢量控制系统具有更好的控制性能。
图9为转子电阻在0.3 s时由0.37 Ω变为0.16 Ω和定子电阻在0.5 s时由0.5 Ω增大为0.9 Ω时,矢量控制系统和参数辨识系统的转矩响应。由图9可知,参数辨识系统的转矩到达稳态的时间相比于矢量控制系统更快,达到稳定转矩的时间缩短了约50 ms。在0.3 s时,施加10 N·m的负载,辨识系统相对于矢量控制系统的响应时间更快,缩短了约8 ms,辨识系统的转矩波动更小,更接近参考值。由于转动惯量和系统阻尼等因素的影响,导致辨识系统和矢量控制系统的转矩比参考值增加了0.5 N·m。在0.5 s时,定子电阻由0.5 Ω增大为0.9 Ω,此时矢量控制系统中励磁和转矩无法正常解耦,导致转矩突然震荡,响应效果变差。
实验结果表明,MRAS与GA-ADRC结合的方法可以有效辨识转子时间常数,从而提高交流异步电机控制系统的控制效果。
4 结论
本文提出了一种MRAS与GA-ADRC相结合的参数辨识方法对转子时间常数进行辨识,使用GA-ADRC对自适应机构中的参数进行优化,并对参数辨识控制系统进行了仿真验证,得出以下结论:
1) 当转子时间常数随电机运行工况变化而改变时,若不能准确修正,会导致电机转速剧烈震荡且无法输出正常转矩。
2) 本文采用MRAS与GA-ADRC相结合的方法对转子时间常数进行辨识,当定子电阻和转子电阻发生变化时,可以准确辨识出转子时间常数的变化,避免转速和转矩出现震荡现象,缩短了转矩达到稳态的响应时间。MRAS与GA-ADRC相结合的方法使交流异步电机控制系统具有良好的动态响应特性,提高了控制系统的抗干扰能力。
