基于紧组合的SINS/DVL/USBL 导航算法
2024-01-13章彩霞刘锡祥黄永江陈世杰陶育杰
章彩霞 ,刘锡祥 * ,黄永江 ,陈世杰 ,陶育杰
(1.东南大学 仪器科学与工程学院,江苏 无锡,214026;2.微惯性仪表与先进导航技术教育部重点实验室,江苏 南京,210096)
0 引言
准确的定位和导航信息是自主水下航行器(autonomous undersea vehicle,AUV)安全、高效作业的关键[1-2]。然而,由于海洋环境的多样性和AUV 的局限性,AUV 很难实现高精度的导航和定位,不能满足日益增长的应用需求。惯性导航系统(inertial navigation system,INS)具有强自主性和强隐蔽性等优点,通常作为AUV 的核心导航系统,但单个传感器无法应对AUV 面临的复杂环境。通过利用各种传感器的互补和特性,进行信息融合和滤波校正,可以在较长时间内获得更高的导航性能和稳定性[3-5]。
多普勒测速仪(Doppler velocity log,DVL)利用多普勒效应进行速度测量,可以为捷联式惯导系统(strapdown inertial navigation system,SINS)提供高精度的速度信息,但位置误差仍然随时间发散[6-7]。超短基线(ultra-short baseline,USBL)定位系统利用声学定位技术实现对水下目标的定位和跟踪,可以获得高精度位置信息,能有效抑制AUV导航系统的位置误差,但受换能器作用距离限制[8-11]。SINS/DVL/USBL 导航系统能充分利用各传感器的特点,取长补短,提高系统外界量测的稳定性,更能满足AUV 高精度、长航时及广区域内的导航与定位的需求。
基于此,张涛等[12]以SINS/USBL/DVL/磁罗经导航(magnetic compass pilot,MCP)组合导航系统为研究对象,较好地判断并隔断处理USBL 故障。王彬等[13]采用单水声应答器和惯导组合的方法抑制INS/DVL 导航误差的发散趋势,有效提高了导航定位精度。张亚文等[14]建立了SINS/DVL 的3 维速度量测模型和SINS/USBL 相对测量信息量测模型后,提出了基于集中滤波的SINS/DVL/USBL组合导航算法,对比SINS/DVL/USBL 联邦滤波的算法具有明显精度优势,但未验证说明复杂水下环境下的精度影响和系统稳健性。徐博等[15]建立了SINS/USBL 子滤波器和SINS/DVL 子滤波器,构建了基于精度因子信息分配方法的SINS/USBL/DVL 联邦滤波器,对于各子滤波器进行动态信息分配,验证了USBL 突然故障的容错性,但对DVL的故障情况并未验证。
分析复杂水下环境对AUV 的影响,应考虑SINS/DVL/USBL 导航系统中DVL 和USBL 的数据出现失效情况,并进行系统精度和稳定性验证。目前公开的SINS/DVL/USBL 组合导航系统在构建SINS/DVL 的量测模型时都选择采用3 维速度量测信息的松组合方法,在DVL 受异常环境影响出现数据失效的情况下,导航精度也会被明显影响。在SINS/DVL 系统中DVL 出现故障的改进方案中,Wang 等[16]提出了基于波束域4 维速度信息的SINS 和DVL 紧组合方法,并验证了所提方法明显优于传统的松组合方法,可以将SINS/DVL的定位精度提高30%以上。Liu 等[17]构建了基于四波束频移信息的组合模型来实现对惯导系统误差和DVL 误差的估计和校正,仿真和实验验证了基于多普勒频移的紧组合模型在水下复杂环境下具有较强的鲁棒性。在DVL 和SINS 的数据融合时,基于DVL 波束信息上的紧组合方法在部分波束失效时能更有效地利用正常的波束信息,提高DVL 数据的利用率。SINS/DVL/USBL 导航在进行数据融合时,也可以采用SINS/DVL 紧组合的数据融合方法以提高导航精度。
基于上述分析,为使AUV 能在复杂水下环境获得更长时间、更高精度以及更稳定的导航定位信息以满足作业需求,提出一种基于紧组合的SINS/DVL/USBL 组合导航算法。首先构建了SINS/DVL的4 维频移信息量测模型和SINS/USBL 的相对测量信息量测模型2 种紧组合模型,并和不同组合模型下的定位精度作比较,仿真验证该算法能有效提高系统的导航精度。为了能够及时有效地处理异常环境带来的失效数据,保证量测信息的稳定性,文中在此基础上对DVL 和USBL 数据失效情况下的定位精度进行故障判断和隔断处理,最终通过理论仿真验证了文中方法在DVL 和USBL 的数据失效情况下具有更高的容错性和稳定性。
1 SINS/DVL/USBL 组合导航模型
考虑集中滤波方法能够获得全局的最优估计,故选取该方法实现SINS/DVL/USBL 紧组合导航,组合导航系统结构如图1 所示。

图1 SINS/DVL/USBL 组合导航系统结构图Fig.1 SINS/DVL/USBL integrated navigation system structrue
导航坐标系(n系)选取为东北天地理坐标系,惯导载体坐标系(b系)、多普勒载体坐标系(d系)和声学基阵坐标系(u系)均选取右前上方向。选择SINS/DVL 四波束方向频移信息量测和SINS/USBL 相对位置信息量测来实现紧组合的集中滤波。
1.1 SINS/DVL/USBL 组合导航状态模型
1.1.1 SINS 子系统状态误差模型
SINS 能够独立自主地提供速度、姿态和位置信息,但会受加速度计和陀螺仪的惯性器件误差影响,故选取传统的15 维惯导系统误差作为SINS子系统的误差状态量
构建SINS 子系统的状态误差方程
式中:WSINS为 零均值高斯白噪声;FSINS为惯导系统矩阵[18]。
1.1.2 DVL 子系统误差模型
影响DVL 测速精度的主要因素有DVL 与SINS 之间的安装角误差、比例因子误差和随机量测误差。因此,选取DVL 比例因子误差和DVL 安装角误差为DVL 子系统的误差状态量
因为安装角误差 δθd为常值,比例因子误差δκd也可近似为1 个常数。建立DVL 子系统的状态误差方程
式中:FDVL=04×4为 DVL 子系统的系统矩阵;WDVL为DVL 的相关噪声矩阵。
1.1.3 USBL 子系统误差模型
由于设备安装原因导致的USBL 安装角误差是USBL 的主要误差源之一。根据USBL 定位原理可知,USBL 的自身测角误差和测距误差也一定程度上影响了USBL 的定位精度。因此,选取USBL 与SINS 之间的安装误差角、USBL 的测角误差和测距误差系数作为USBL 子系统的误差状态量,即
USBL 设备中一般需要结合深度计(pressure sensor,PS)进行深度测量,考虑PS 输出模型为
式中:h为高度真值;δbPS为PS 的常值偏置误差;ωPS为零均值高斯噪声。
故将δbPS加 入到USBL 子系统状态变量中,得
因为 δα、δβ和 δκu均为小量,可视为随机常数,建立USBL 子系统的状态误差方程为
式中:FUSBL=07×7为USBL 子系统的系统矩阵;WUSBL为USBL 和PS 的相关噪声矩阵。
1.1.4 SINS/DVL/USBL 状态误差模型
综上所述,构建SINS/DVL/USBL 集中滤波系统时选取状态变量为
建立系统的状态误差方程为
1.2 SINS/DVL/USBL 组合导航量测模型
文中设计的SINS/DVL/USBL 组合导航系统的量测模型主要由SINS/DVL 四波束方向频移信息量测和SINS/USBL 相对测量信息量测组成。
1.2.1 SINS/DVL 频移量测模型
DVL 采用十字型四波束Janus 配置,4 个换能器波束发射方向与d系z轴反方向的夹角为为DVL 测量的三向速度信息,如图2 所示。
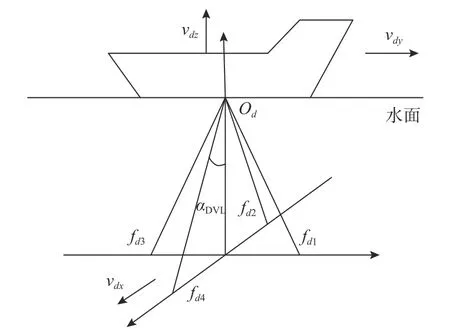
图2 DVL 十字型四波束Janus 配置Fig.2 DVL cross-type four-beam Janus configuration
四波束方向多普勒频移构成的列向量为
根据DVL 的3 维速度信息解算四波束方向的频移信息公式为
利用SINS 测量的导航系速度信息计算出四波束方向的频移值为
DVL 实际频移测量值为
式中,vd为多普勒测速仪的频移量测噪声。
因此,根据式(13)和 式(14)建 立SINS/DVL 的频移量测为
由式(15)可得量测矩阵为
1.2.2 SINS/USBL 相对测量信息量测模型
参考文献[11],将USBL 输出的方位角、高度角和斜距测量值与惯性导航系统计算的测量信息进行对比,得到的差值作为SINS/USBL 的量测量。
USBL 测量的方位角、高度角和斜距为
SINS 计算的USBL 高度角误差δ αSINS,方位角误差 δβSINS和 斜距误差系数 δρSINS为
式中,L和λ分别为载体的纬度和经度。
所以,根据式(17)和式(20)建立SINS/USBL的相对测量信息量测为
根据PS 的输出模型,将SINS 的高度信息和PS 的深度信息输出之差作为高度信息量测
由式(25)和(26)可得SINS/USBL 子系统的量测方程为
量测矩阵为
1.2.3 SINS/DVL/USBL 量测模型
文中构建的SINS/DVL/USBL 紧组合导航系统的量测量为
对应构建的量测方程为
2 SINS/DVL/USBL 故障判断及处理
2.1 基于新息的 χ2故障检测
为了保证集中卡尔曼滤波的量测稳定性,当DVL 和USBL 的数据出现异常时,对其进行隔断处理。文中采用 χ2检验法来判断DVL 和USBL 的测量值是否出现异常。
新息序列定义为
新息的协方差矩阵为
2.2 DVL 失效数据处理
在判断DVL 存在失效数据或野值时,采取数据隔断处理,系统的量测方程简化为
2.3 USBL 失效数据处理
当USBL 受环境影响出现野值时,采取数据隔断处理,系统的量测方程简化为
3 理论数据仿真分析
为验证算法有效性,进行如下仿真研究。仿真时间为2 185 s,载体初始地理位置为L=39.8◦,λ=116.2◦,h=0 m,以4 m/s 的速度按图3 所示轨迹匀速航行,其中应答器的位置为Pt=[39.802 026°116.198 185° -150 m]。为确保算法定位精度,屏蔽各类误差,设置初始姿态角均为 0◦,无初始速度误差和位置误差。模拟中等海平面设置摇摆运动如下[17]
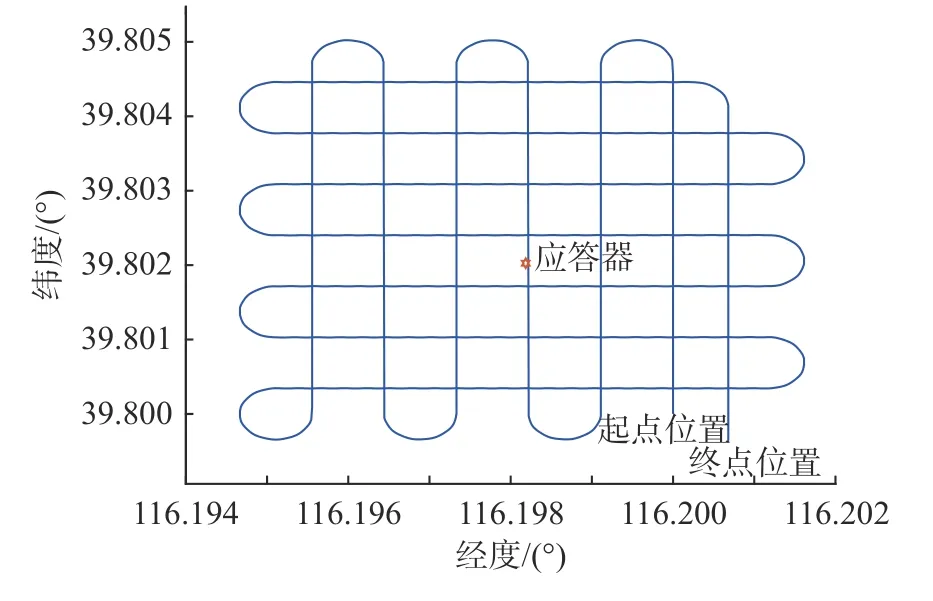
图3 仿真轨迹Fig.3 Simulation track
式中: θm=3◦;γm=4◦;ψm=3◦;初始相位角 θ0=3◦;γ0=4◦;ψ0=3◦;摇摆周期分别为5、6、7 s。
SINS 的数据更新频率为200 Hz,DVL、USBL和PS 的数据更新频率均为1 Hz[19-20]。各传感器的误差参数设置如表1 所示。

表1 传感器误差参数Table 1 The error parameters of sensors
3.1 不同组合模式仿真对比
按照文中的SINS/DVL/USBL 紧组合导航算法进行仿真,并对SINS/DVL 频移量测紧组合导航算法、SINS/USBL 相对位置信息量测紧组合导航算法、文献[14]中SINS/DVL/USBL 的SINS/DVL速度量测和SINS/USBL 相对测量信息量测集中滤波方法定位结果进行对比。SINS/DVL 紧组合滤波方法表示为SDT,SINS/USBL 紧组合滤波方法表示为SUT,文献[14]的方法用SDLUT表示,文中方法用SDTUT表示。定位误差曲线如图4~图6 所示。

图4 东向位置误差Fig.4 East position error

图5 北向位置误差Fig.5 North position error

图6 水平定位误差Fig.6 Level position error
由定位误差曲线可以看出,SINS/DVL/USBL紧组合集中卡尔曼滤波算法和基于速度量测和相对测量信息量测的SINS/DVL/USBL 集中滤波方法的定位精度都明显优于SINS/DVL 紧组合方法和SINS/USBL 紧组合方法,具有更高精度。
计算各个方法的水平定位误差的均方根误差(root mean squared error,RMSE)可以发现(见表2),文中方法对比基于速度量测和相对测量信息量测的SINS/DVL/USBL 集中滤波方法具有更高精度,精度提升约23%。
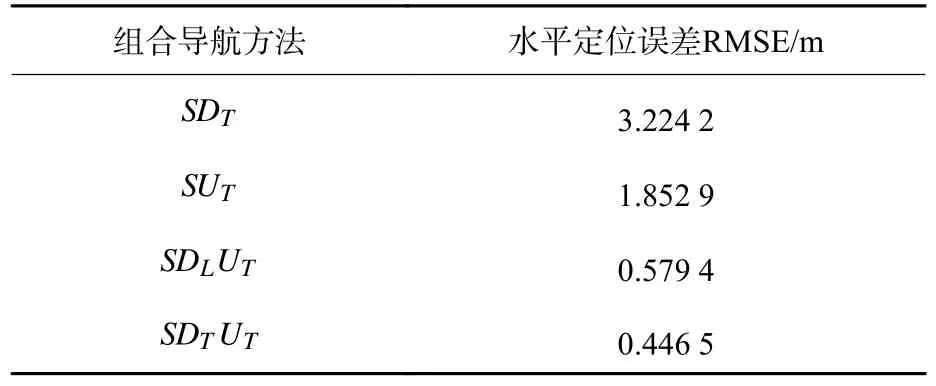
表2 不同组合导航方法水平定位误差RMSE 对比Table 2 Comparison of level positioning error RMSE
3.2 DVL 和USBL 数据失效情况下的仿真对比
在实际复杂的水下环境,DVL 会出现原始波束频移数据中部分波束数据失效的情况,USBL 的输出水声信息也存在野值。为了仿真这种情况,对DVL 和USBL 的原始数据以10%概率加上原来50 倍的量测噪声,DVL 和USBL 存在失效数据的仿真情况如图7 和图8 所示。

图7 DVL 失效数据情况Fig.7 DVL failure data situation

图8 USBL 失效数据情况Fig.8 USBL failure data situation
在DVL 和USBL 出现数据失效的情况下,通过卡方检验判断出故障情况并进行隔离处理。对比2 种采用不同量测的集中卡尔曼导航算法,DVL 数据失效情况和USBL 数据失效情况下水平定位误差曲线如图9 和图10 所示。计算数据失效情况下的定位误差RMSE,并与正常情况的定位误差作对比,如表3 所示。
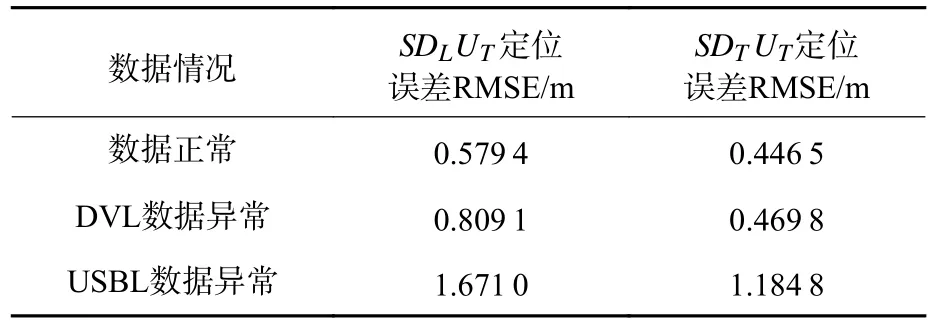
表3 数据失效情况下不同量测的集中滤波方法水平定位误差RMSETable 3 Level positioning error RMSE of the concentrated filter methods based on different measurements in case of data invalidation

图9 DVL 数据失效情况下的水平定位误差Fig.9 Level positioning error in case of DVL data failure

图10 USBL 数据失效情况下的水平定位误差Fig.10 Level positioning error in case of USBL data failure
观察定位误差曲线,并对比2 种方法的定位误差RMSE,可以发现,在DVL 数据失效情况下,文中方法可以实现定位精度基本稳定,定位误差较正常情况增长5.2%,而SDLUT方法定位误差较正常情况增长39.6%。在USBL 数据失效情况下,定位精度会受到较大影响,文中方法定位误差较正常情况增长165.4%,而SDLUT方法定位误差较正常情况增长188.4%,精度仍明显优于基于速度量测和相对测量信息量测的SINS/DVL/USBL 集中滤波方法。综上所述,无论是DVL 数据失效还是USBL 数据失效的情况,文中方法都具有较高的精度和稳定性,更适应复杂的水下环境。
4 结束语
针对复杂水下环境下AUV 对于高精度、高稳定性和高可靠性的导航需求,提出一种基于DVL四波束方向频移量测和USBL 相对测量信息量测的SINS/DVL/USBL 紧组合导航算法,针对数据失效情况进行实时判断并隔断处理。仿真验证表明,与SINS/DVL 紧组合导航方法、SINS/USBL 紧组合导航算法及基于DVL 速度量测和USBL 相对测量信息量测的SINS/DVL/USBL 集中滤波组合导航算法相比,该方法具有较高的定位精度,可提升约23%。在DVL 和USBL 数据失效的情况下,该算法稳定性更好,在DVL 数据失效时,定位误差较正常情况仅增长5.2%;在USBL 数据失效时,定位误差较正常情况增长165.4%,优于基于其他量测的SINS/DVL/USBL 集中滤波导航算法,具有更强的鲁棒性,更能适应复杂的水下环境。
文中方法对于DVL 和USBL 的数据直接进行数据隔断以避免故障数据带来的精度影响,但是如果存在长时间的数据失效情况,隔断可能会影响定位精度,下一步将针对DVL 和USBL 的数据情况研究如何采取更有效的手段(而非数据隔断)进行数据替换。
