电磁搅拌模式对大方坯结晶器内钢水流动特性的影响
2024-01-12梅德云杨湘澜铉明涛
梅德云, 陈 敏, 杨湘澜, 铉明涛
(东北大学 冶金学院, 沈阳 110819)
近年来,随着钢铁行业的发展进入相对低迷阶段,产品质量对市场竞争力的影响变得更为突出.提高钢材质量始终是钢铁工业发展的重要方向之一.结晶器在连铸生产过程中对净化钢质起着关键性的作用,其内部钢液流动状态对夹杂物的排除、保护渣的卷入及凝固坯壳的形成等均具有重要影响,并且还会进一步影响铸坯的表面和内部质量[1].众所周知,结晶器电磁搅拌(MEMS)是提高铸坯质量的重要技术手段.其工作原理是借助在铸坯的液相穴内感生的电磁力加强钢水在液相穴内的运动,以此增强钢水的对流、传热及传质过程,改善、消除结晶器内钢水的过热度,提高铸坯的等轴晶率[2].
电磁搅拌的参数因断面和钢种的不同而有所差异,合理的电磁搅拌参数有利于充分发挥电磁搅拌的冶金效果,使结晶器内钢液的流动状态更好,从而改善铸坯质量.对于连铸电磁搅拌过程的分析,采用单一的理论分析很难得到直观的结果,但随着科学技术的发展,利用计算机进行模拟仿真已经成为研究连铸电磁搅拌的重要手段.关于电磁搅拌模式对电磁场、流场及凝固坯壳的影响已经有过很多相关研究[3-8],这些研究不仅有助于理解电磁场与流场的耦合行为,也为优化连铸工艺参数提供了重要的参考依据.
尽管电磁搅拌的数值模拟研究取得了许多进展,正反转交替式电磁搅拌模式也有诸多应用[9-11],但因存在铸坯断面尺寸、钢种、M-EMS 结构与参数、安装位置等差异,电磁搅拌的应用效果也不尽相同.某厂新建奥钢联大方坯连铸机配有M-EMS,但外方未提供具体的电磁搅拌技术方案,故M-EMS 不能有效发挥电磁搅拌效果.本文中拟通过建立250 mm×300 mm 的大方坯结晶器内电磁场和流场的耦合数学模型,在考察拉速、浸入式水口结构、浸入深度等因素对结晶器内流场影响的基础上,进一步探究M-EMS 搅拌电流强度和搅拌模式等因素对结晶器内流场的影响规律,并重点分析搅拌电流强度和间歇反转对结晶器内流场的影响,以期为电磁搅拌模式参数的优化提供可靠的理论依据.
1 数学模型的建立
1.1 模型假设
为了简化模型及突出电磁搅拌对钢液流动的影响,在建模时需要做出如下假设:①忽略结晶器的锥度、振动及凝固坯壳,不考虑空气的影响;②电磁搅拌器内有冷却水和其他附属设备,均处理成空气;③搅拌器绕组线圈是由多根密排的铜质导线缠绕而成,将线圈简化成具有相同导电面积的导电区域;④假定钢液为不可压缩牛顿流体,其物性参数为常数;⑤在结晶器电磁搅拌过程中,钢液的磁雷诺数远小于1,故在计算电磁场时不考虑钢液流动的影响;⑥由结晶器电磁搅拌激发产生的磁场属于磁准静态场,其产生的位移电流影响很小,故在计算中忽略位移电流;⑦忽略电流变化过程,电磁力以时均值表示.
1.2 控制方程
1.2.1 电磁场控制方程
基于麦克斯韦方程组和本构方程建立电磁场的控制方程.
磁通连续性原理:
电磁感应定律:
安培环路定律:
高斯通量定理:
本构方程:
在计算中选用库仑规范条件,其表达式为
将式(8)~(10)代入麦克斯韦方程组及本构方程,经整理可得:
电磁力:
1.2.2 流动控制方程
流体的流动可以用连续性方程、动量方程及湍流k-ε方程来描述.连续性方程:
动量方程:
湍动能k方程:
湍动能耗散率ε方程:
其中:
式中:ρ为流体密度,kg/m3→ 为速度,m/s;P为压力,Pa;μeff为有效黏度系数,μ和μt分别为分子和湍流黏度系数,kg/(m·s);为重力加速度,取9.8 m/s2为表面张力,N/m3;为单位张量;k为流体湍动能,m2/s2;ε为湍动能耗散率,m2/s3;C1ε,C2ε,Cμ,σk,σε皆为经验系数,分别取1.44,1.92,0.09,1.0,1.3.
1.2.3 多相流模型
采用VOF 方法追踪钢液-钢渣界面波动情况,假设局部控制体积中第q种流体的体积分数为αq(q=1 代表钢液,q=s代表液态保护渣),流体局部控制体积中的各相的体积分率之和为1.求解相的体积分率可以追踪自由界面,则对于第q相有:
式中:ρq为q相的密度,kg/m3;αq为q相的体积分数;为第q相的速度,m/s.
混合相体积密度:
混合相黏度:
采用连续表面力(continuum surface force,CFS)模型来考虑相间表面张力的作用,并将其作为体积力加载到动量方程源项,其表达式如下:
式中:σ为表面张力系数,N/m;Vq为控制体q的体积,m3;κq为自由表面的平均曲率,其定义为
式中:为垂直于表面的单位矢量.
1.3 边界条件和物性参数
结晶器实际长度为800 mm,为避免在模拟过程中产生结晶器出口回流,将模型计算长度扩展至1 600 mm.图1 为结晶器空载电磁搅拌器的有限元模型.为了保证计算的精度和准确性,在计算域实体外建立直径为3 m 的空气域.不同材料的物性参数及结晶器和电磁搅拌器模型的结构与工艺条件见表1.具体边界条件如下: ①设定垂直于入口的流动速度,入口速度利用质量守恒定律由拉速换算确定;②设模型出口处流动充分发展,即各物理量沿该截面的法向导数为0;③模型顶面设为自由液面,垂直于液面的速度分量及所有其他各变量沿液面法线方向的梯度设为0;④在结晶器壁面和水口壁面处,垂直于壁面的速度分量为0,而平行于壁面的分量采用移动边界;⑤在靠近结晶器壁和水口壁的近壁区节点上,平行于壁面的分量由壁面函数确定;⑥力线与包围搅拌器空气的外表面平行,设定空气外边界电磁场为0;⑦向线圈加载三相交流电,相邻两线圈的相位差为120°.

表1 物性参数、模型结构与工艺条件Table 1 Physical parameters, geometrical dimensions,and operational conditions
电磁场方程采用ANSYS 进行简谐态计算,收敛标准为10-4.流场采用FLUENT 进行计算,动量和湍流方程采用二阶迎风格式进行离散,体积分数方程采用Geo-Reconstruct 格式进行离散,离散后的方程采用PISO 算法进行求解,模拟计算的时间步长为0.005 s,收敛标准为10-5.电磁场求解结束后,将电磁力以插值的方式向动量方程加载.对于连续搅拌与不搅拌,选用计算至物理量稳定时(120 s)的结果进行分析;对于交替搅拌,选用物理量与前一波动周期最大波动相差3%以内的结果进行分析.
2 结果与讨论
2.1 模型验证与流场基本特性
图2 为空载(无钢液)条件下结晶器中心线上电磁强度计算值与实测值的对比结果.由图可知,计算的电磁强度值与现场实测数值基本相等,验证了模拟结果的准确性.同时还可看出,磁场强度沿电磁搅拌器长度的中心面呈对称分布,结晶器下部磁场强度高于中上部的磁场强度.
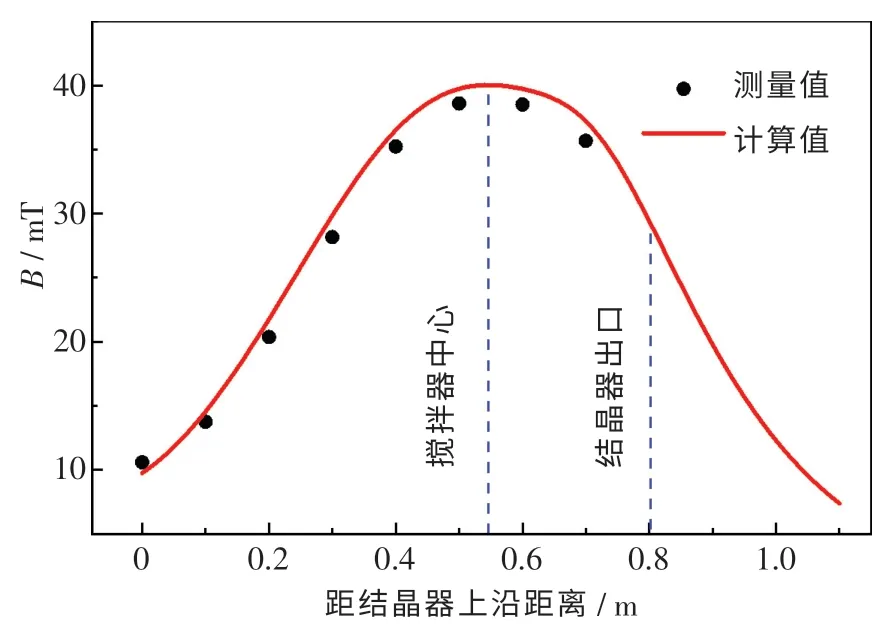
图2 计算结果与实测结果对比图Fig.2 Comparison of the calculated and measured results
图3 示出了无电磁搅拌和有电磁搅拌对结晶器内钢液迹线的影响,且均为计算至稳定时(120 s)的结果.当未采用电磁搅拌时,由浸入式水口侧孔流出的钢液分别向上和向下运动,形成典型的上下回流,自由液面流速小于0.03 m/s[见图3(a)].当采用电磁搅拌后,结晶器内钢液在电磁力的作用下形成了沿水平方向运动的环流[见图3(b)].在搅拌器中间位置,由于电磁强度最高,钢液的环流速率也最大.在搅拌电流强度为400 A、单方向连续搅拌的条件下,自由液面的钢液流速增至大于0.10 m/s.因此,可以认为当采用结晶器电磁搅拌后,结晶器内钢液的流动特征发生了根本性的变化.
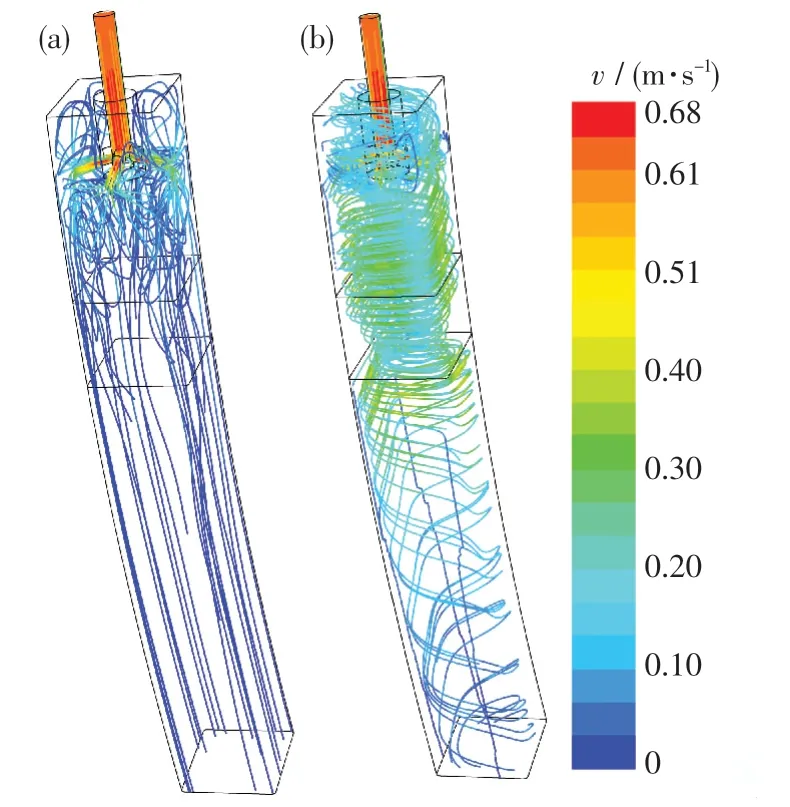
图3 无电磁搅拌和有电磁搅拌对结晶器内钢液迹线的影响Fig.3 Effect of no electromagnetic stirring and electromagnetic stirring with the trace chart of the molten steel in the mold
图4 为采用四侧孔浸入式水口时结晶器内的钢液速度分布云图.在未采用电磁搅拌时,下回流可形成220~260 mm 的冲击深度[见图4(a)].众所周知,下回流形成的冲击深度会将高温钢液带至结晶器深处,使钢水热量的散失得到减少.但由于高速流动区集中在浸入式水口附近,这会使其他区域钢液的混匀程度不高.在搅拌电流强度为400 A、单方向连续搅拌的条件下,水平方向的电磁力可阻碍侧孔流股的运动,使流股无法到达结晶器壁,不再形成典型的上下回流而是水平流动[见图4(b)].受电磁搅拌影响的区域都存在水平流动,使得钢液内部较活跃,这有助于均匀钢液的成分和温度.
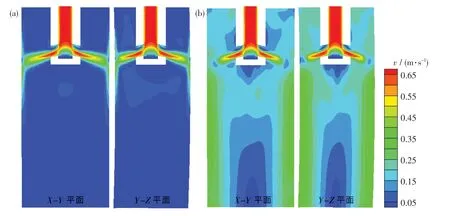
图4 结晶器内钢液速度分布云图Fig.4 Velocity cloud atlas of the molten steel in the mold
2.2 搅拌电流强度的影响
图5 和6 分别示出了搅拌电流强度对自由液面速度和湍动能分布的影响.从图中可以看出,自由液面流场以浸入式水口为中心,呈中心对称形式分布,且液面流速在铸坯厚度方向上略高于宽度方向.当搅拌电流强度为300 A 时,电磁搅拌产生的旋流无法到达自由液面,造成液面流速和湍动能仅为0.000 16 m2/s2,0.11 m/s,与无电磁搅拌时液面情况相近.随着搅拌电流强度的增大,液面的活跃程度显著增强,液面湍动能和流速可分别由400 A 时的0.001 2 m2/s2,0.27 m/s 增至500 A时的0.001 6 m2/s2,0.32 m/s,以及600 A 时的0.002 6 m2/s2,0.40 m/s.与由400 A 增至500 A相比,由500 A 增加至600 A 的液面流速和湍动能的增幅更大,而液面流速和湍动能过大会发生卷渣现象,故不适宜再继续增大搅拌电流强度.
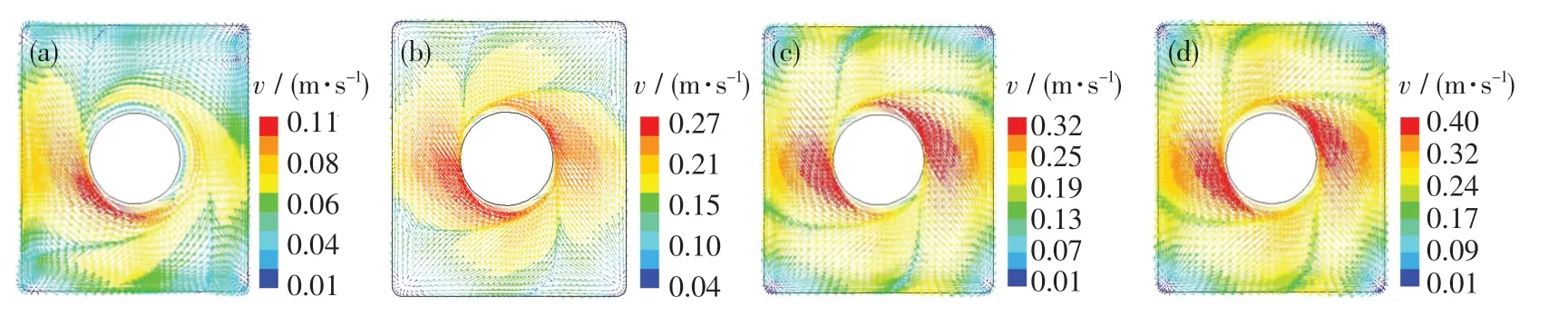
图5 搅拌电流强度对自由液面速度的影响Fig.5 Influence of stirring current intensity on velocity of the molten steel in free surface
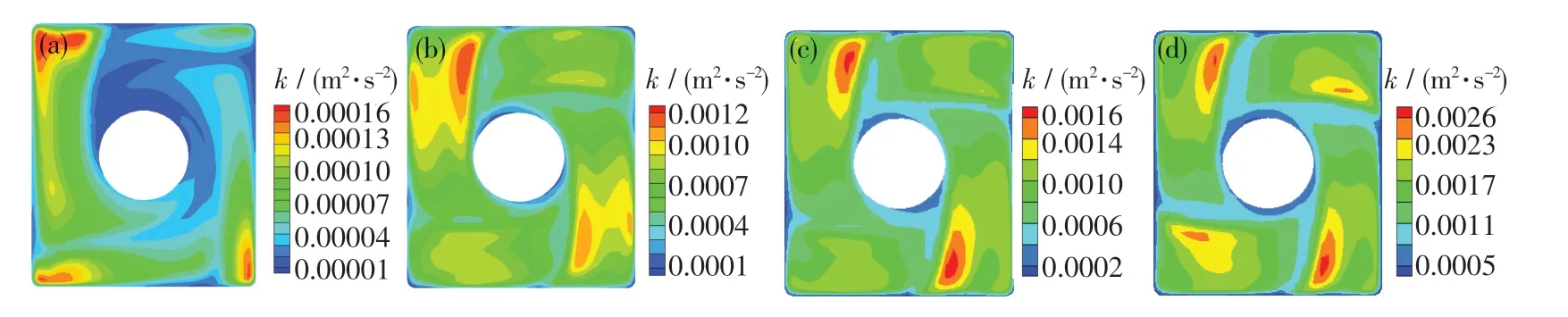
图6 搅拌电流强度对自由液面湍动能的影响Fig.6 Influence of stirring current intensity on turbulent kinetic energy of the molten steel in free surface
2.3 搅拌模式的影响
图7 示出了搅拌电流强度400 A 时的自由液面特征,图7 (a)为单向连续搅拌计算至稳定时(120 s)的液面形状;图7(b)~(e)为正反转交替式搅拌至第8 周期不同时刻的液面形状.当采用连续搅拌时,液面最大流速为0.18 m/s.同时,由于电磁力的旋流作用,结晶器内液面形成了明显的凹陷,最大液位差可达8 mm 左右.但在采用正反转交替式电磁搅拌时,正反交替电磁力不仅阻碍了钢液的持续单向旋转,同时还阻碍了动量向自由液面的传递,故可有效降低钢液流速和液位差.此时,在搅拌电流强度400 A 的条件下,钢液最大流速小于0.06 m/s,最大液位差小于1 mm.
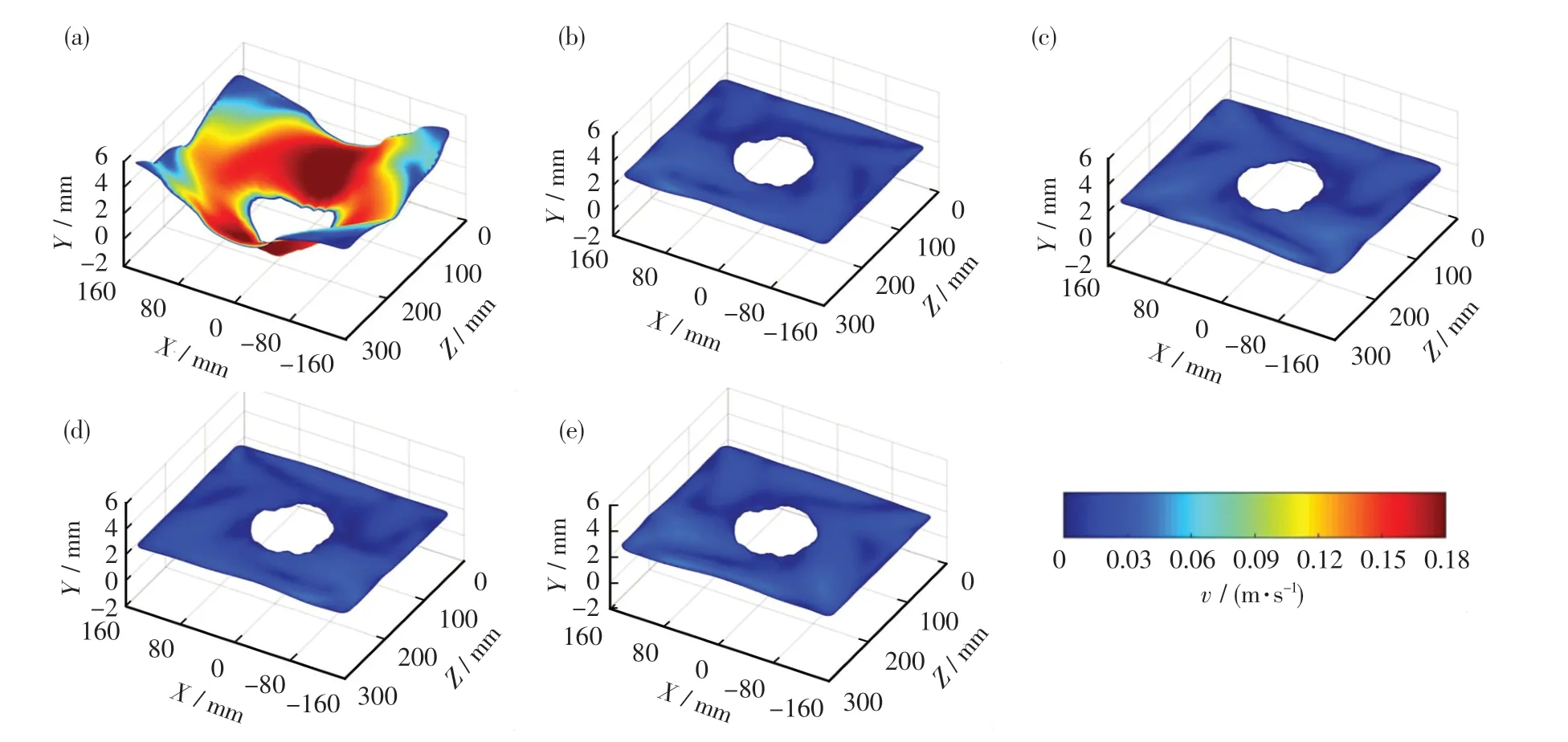
图7 单向连续搅拌和正反转交替式搅拌自由液面的形状Fig.7 Shape of free surface under unidirectional stirring and different stage of alternating stirring
图8 示出了搅拌电流强度为400 A 时正反转交替式电磁搅拌的间歇时间对液面流速及液位差的影响.为了充分发挥电磁冶金的作用,电磁搅拌的停歇时间越短,越有利于提高电磁搅拌效率.但由图8 可知,当停歇时间为2,5,8 s 时,液面流速时均值分别为0.047,0.049,0.048 m/s,液面流速峰值分别为0.057,0.063,0.057 m/s,最大液位差的时均值相差不大,均在2.10 mm 左右,最大液位差的峰值分别为2.26,2.18,2.17 mm.其中,停歇时间为2 s 时的最大液位差峰值较大,最易发生卷渣现象,而停歇时间为5 s 与8 s 的液位差大致相当,但5 s 时的液面流速时均值和峰值都比8 s时的稍大.这是因为当停歇时间为2 s 时,结晶器内的液面流速下降较小,钢液仍具有一定的运动惯性,此时加入反向电磁力容易形成对液面的扰动,使得液面波动较大.而当停歇时间大于5 s之后,停歇时间对液面波动的影响明显降低,故停歇时间不宜小于5 s.

图8 间歇时间对自由液面流速和液位差的影响Fig.8 Influence of intermittent time on velocity and liquid level difference of the free surface
图9 示出了采用正反转交替式电磁搅拌时电流加载时间与搅拌电流强度对结晶器内自由液面流速的影响.由图可知:当搅拌电流强度为400 A时,随着电流加载时间的延长,自由液面的流速时均值逐渐由0.043 m/s 增至0.051 m/s,峰值从0.048 m/s 逐渐增至0.074 m/s,但液面流速远小于0.10 m/s 这一经验值[1];当搅拌电流强度为500 A 时,随着电流加载时间的延长,液面流速时均值逐渐由0.048 m/s 增至0.11 m/s,峰值分别为0.061,0.10,0.14,0.18 m/s.值得注意的是,当电流加载时间为15 s 时,最大流速已明显高于0.10 m/s,而加载时间为10 s 时的最大流速为0.10 m/s.因此,综合考虑电磁搅拌对液面波动的影响和电磁利用率问题,搅拌电流强度500 A、加载时间10~15 s 的电磁搅拌模式最佳.
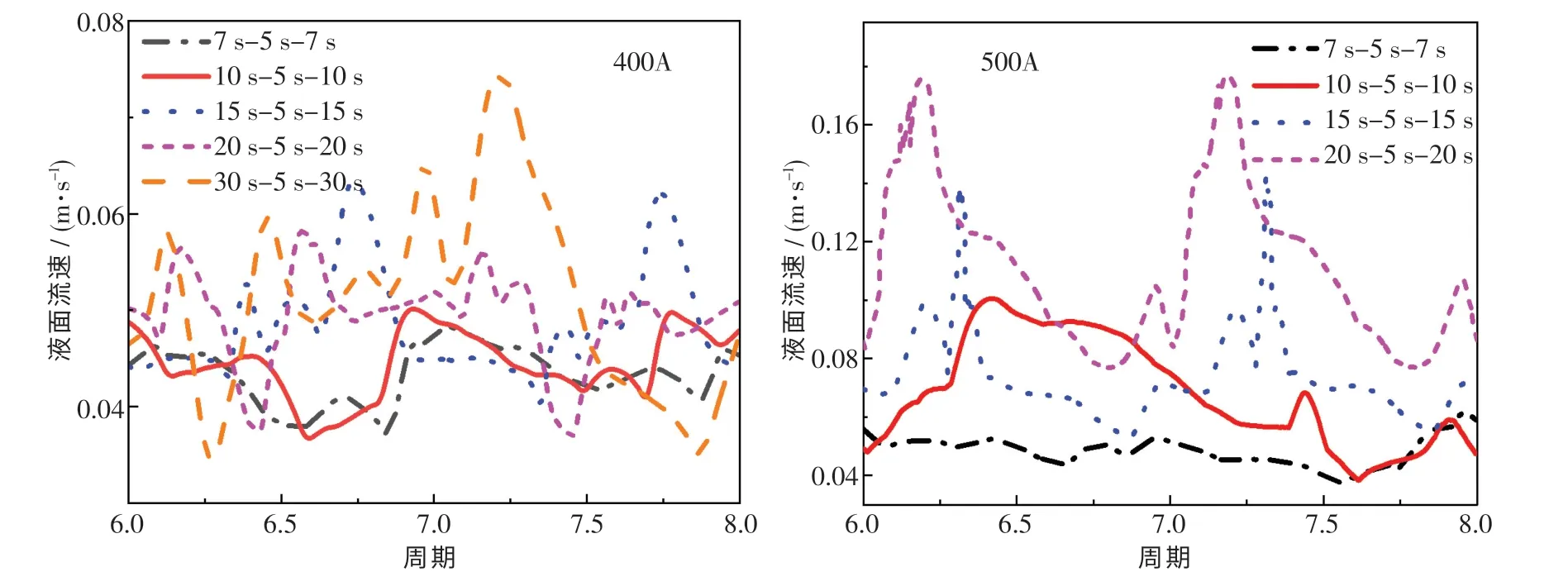
图9 电流加载时间对自由液面流速的影响Fig.9 Influence of load-time of current on velocity of the molten steel in free surface
图10 示出了采用正反转交替式电磁搅拌时电流加载时间与搅拌电流强度对结晶器出口最大流速的影响.由图10 可看出:随电流加载时间的增加,在搅拌电流强度为400 A 时,结晶器出口处钢液流速时均值由0.22 m/s 逐渐增至0.33 m/s,峰值由0.33 m/s 逐渐增至0.41 m/s;在搅拌电流强度为500 A 时,结晶器出口处钢液流速时均值由0.30 m/s 逐渐增至0.41 m/s,峰值由0.47 m/s增至51 m/s.但在搅拌电流强度为400 A 时,当电流加载时间大于15 s 后,出口处钢液流速出现平台期,动量向周围传播与耗散,使电磁搅拌未得到充分利用.在搅拌电流强度为500 A 时,当电流加载时间大于10 s 后,加载时间对结晶器出口钢液流速的影响不再明显,故加载时间不宜超过15 s.
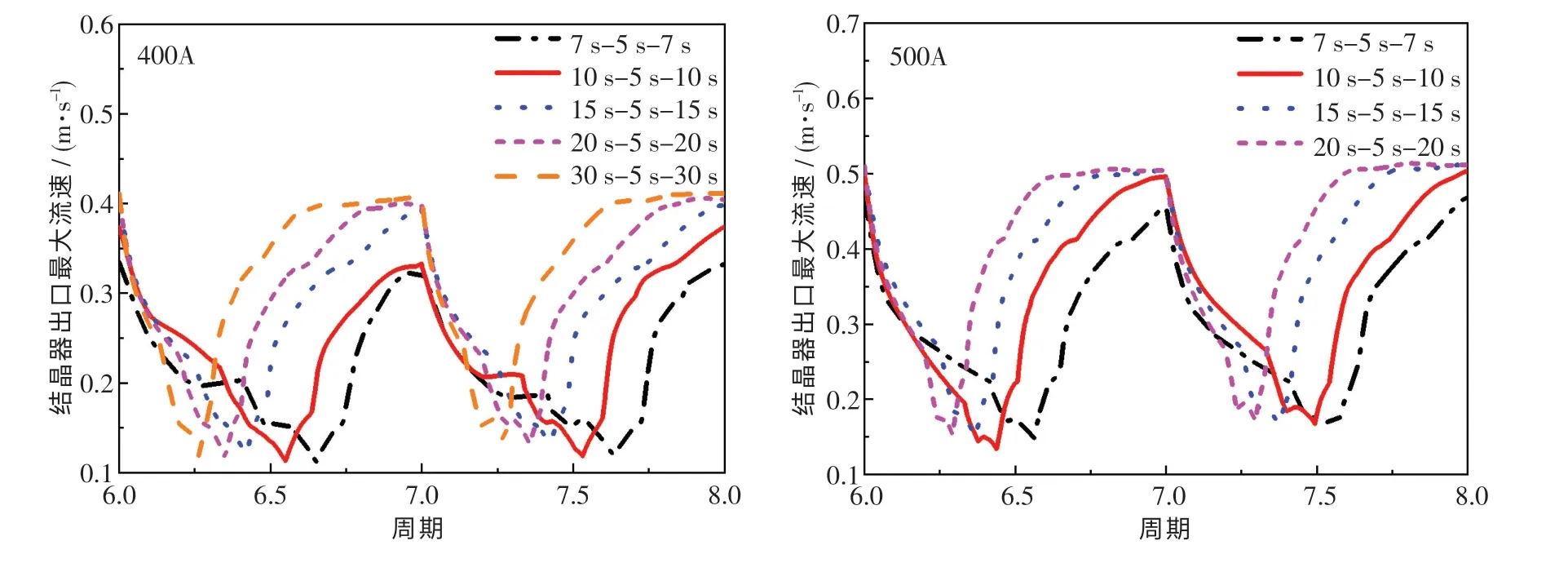
图10 电流加载时间对结晶器出口最大流速的影响Fig.10 Influence of load-time of current on maximal velocity of the molten steel on mold exit
2.4 实际应用效果
图11 示出了采用双丝法[12]测量不同搅拌模式下窄面中心线上液渣层厚度的分布情况.由图可知:当采用连续搅拌时,液渣层厚度由窄面附近的10.0 mm 增至水口附近的13.0 mm;当采用交替式搅拌时,窄面附近的液渣层厚度为9.0 mm,且在整个宽度方向的液渣层厚度分布较为均匀,水口附近的液渣层厚度仅为10.5 mm.尽管采用交替式搅拌时液渣层厚度略有下降,但可通过优化保护渣性能进行调整.此外,对断面尺寸250 mm×300 mm 的GCr15 钢铸坯水浸探伤,结果表明:一级探伤和二级探伤均合格,铸坯中未检测到大于27 μm 的非金属氧化物夹杂;GCr15 钢铸坯的平均等轴晶率由优化之前的平均50%增至55%以上,铸坯中心的最大偏析度从1.16 降至1.10.总之,采用优化M-EMS 工艺后,液渣层分布均匀性与铸坯质量均得到改善,达到了技术攻关的效果.
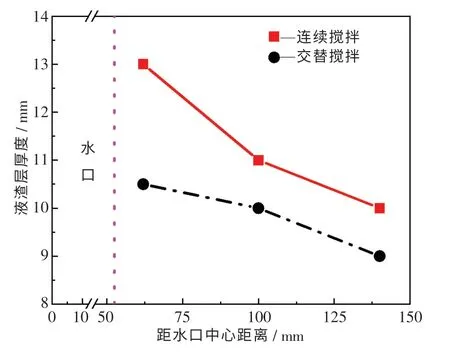
图11 搅拌模式对不同位置处液渣层厚度的影响Fig.11 Effect of stirring mode on the thickness of the liquid slag layer at different locations
3 结 论
(1)M-EMS 可从根本上改变结晶器内钢水的流动特性.结晶器内钢液由无电磁搅拌时的上下流动为主转变成水平流动为主,且伴随钢水的流速明显增加.此外,电磁搅拌方式还可影响自由液面的形状,采用连续单向电磁搅拌时自由液面会形成明显凹陷.
(2)采用正反转交替式电磁搅拌方式,既可使结晶器内的流动呈周期性变化,又能大幅度降低结晶器的液面活跃程度.此外,增加电磁搅拌的电流加载时间还能使结晶器内钢液流速峰值增加.综合考虑电磁搅拌效果和电磁利用率,搅拌电流强度为500 A、电流加载时间为10 ~15 s、间歇时间不小于5 s 是最适宜的电磁搅拌模式.
(3)采用优化电磁搅拌工艺后,浇注GCr15轴承钢时的结晶器液渣层分布均匀性明显改善,铸坯质量也得到了提高.
