电极更换对电渣重熔过程金属液和熔渣凝固的影响

黄 烁， 段怡如， 李连鹏， 段 然， 刘中秋， 李宝宽

（1.北京钢研高纳科技股份有限公司， 北京 100081；2.东北大学 冶金学院， 沈阳 110819； 3.抚顺特殊钢股份有公司， 辽宁 抚顺 113001）

高温合金透平轮盘锻件作为先进重型燃气轮机的关键热端部件之一，制备技术长期依赖进口，在关键技术上受制于人，这极其不利于我国重型燃气轮机的自主发展.随着国内大型冶炼和锻造等重型装备组件的投产使用，氩气保护气氛电渣重熔炉（PESR）已用来生产大尺寸GH4706 高温合金轮盘锻件.然而受国内PESR 炉电极支臂承重能力限制，单支电极的质量不能超过12 t，故只能采用电极更换技术来重熔超过12 t 级的铸锭.整个电极更换过程需要经历以下4 个阶段：第1阶段为原电极稳定熔炼阶段；第2 阶段为原电极脱离阶段，原电极熔炼完成脱离渣池，电源断开，热源消失，准备更换原电极，但是新电极还未插入渣池内；第3 阶段为新电极加热阶段，电源接通，热源恢复，新电极插入渣池但未熔化；第4 阶段为新电极熔化阶段，新电极开始熔化，直至达到电极的目标熔速.在整个过程中，电渣重熔原本的稳定性被破坏，这对电磁场、温度场、流场及凝固熔化等将产生影响.

Jackson 等［1］探讨了电极更换对电渣重熔过程热平衡及凝固熔化的影响，提出了原电极脱离的最长时间应该控制在金属凝固量低于熔池体积5%的想法，并采用电极和渣池预热的方式来降低电极更换对电渣重熔过程的影响.Karimi-Sibaki等［2］探究了原电极脱离阶段的热量损失，发现结晶器的热损失几乎保持不变，然而渣／空气界面的热损失明显增多，但是他们未考虑电极熔化金属液滴的滴落及电极更换的其他阶段.

目前，关于高温合金电极更换对电渣重熔过程影响的研究比较缺乏，若充分了解并优化此过程，可以有效提高大型铸锭的质量.因此，本文中建立电渣重熔过程的磁热流瞬态耦合模型，探究电极更换对高温合金电渣重熔过程电磁场、温度场、流场及凝固熔化的影响，并分析新电极的不同预热温度对电极端部形成凝固渣的影响.

1 数学模型

1.1 控制方程

采用有限体积法同时求解电渣重熔过程中的电磁场、温度场和多相流动.详细的数学模型见文献［3］，本文中只给出简单的控制方程.

采用旋转矢量法求解麦克斯韦方程，磁场强度写成复数的实部形式［4］：

式中：是磁场强度，A／m；是磁场强度的复数形式；ejωt是复数的指数形式；j是虚数单位；ω是角频率，s-1；t是时间，s.

本文中采用二维轴对称模型，磁场强度只有方位角分量，因此麦克斯韦方程可以写成如下形式［5-6］：

式中：是方位角方向的磁场强度，A／m；z是方向；r是半径；σ是电导率，S／m；μ是真空磁导率，H／m.

电流密度J由磁场强度计算得到：

利用上述得到的电流密度和磁场强度，求解洛伦兹力和焦耳热［7-8］.

式中：J是电流密度，A／m2；F是洛伦兹力，N；Q是焦耳热，W.

对洛伦兹力和焦耳热进行时均处理：

式中：Fjh是电流密度和磁场强度相乘的结果；Jr，Ji分别是电流密度的实部和虚部；Hr，Hi分别是磁场强度的实部和虚部；请注意这里Fjh和F代表不同的物理量，Fjh只是求解时均洛伦兹力的方法.

采用VOF 法跟踪渣／金界面，采用连续性方程和Navier-Stokes 方程模拟熔渣和金属液的两相流动［9-10］.

式中：ρ是密度，kg／m3；t是时间，s；v是速度，m／s；p是压力，Pa；μeff是有效黏度，Pa／s；Fst是熔渣和金属液相间的表面张力，N；Fe是洛伦兹力，N；Fd是糊状区阻力，N；Ft是由密度差产生的热浮力，N.在电渣重熔流动中，最大雷诺数主要由液滴滴落引起的，这是一种低雷诺流动，因此采用k-ε模型来计算湍流黏度［3，11］.

将电磁场产生的焦耳热作为源项添加到能量方程中，但电渣重熔过程中会发生凝固现象，因此存在相变.为了准确预测电渣重熔过程中的温度场和凝固过程，本文中采用内能形式的能量守恒方程［12-13］.

式中：ρ是混合相密度，kg／m3；E是混合相内能，J；keff是有效导热率，W／（m·K）；ΔT是温度差，K；f1是液相分数；L是熔化潜热，J／（kg·K）.

1.2 边界条件

计算域的边界如图3 所示.磁场强度方位角分量在电极入口和铸锭底部是连续的，而在渣池顶部及铸锭和渣池的侧壁是与电流有关.

电极入口和铸锭底部：

渣池顶部以及铸锭和渣池的侧壁：

1.2.2 电极熔化速率边界

采用电极与渣池之间的瞬态传热模型计算电极熔化速率［14］，如式（13）所示.以电极顶端和端部的温度作为边界条件，采用求解常微分方程的方法得到电极内部沿径向的温度分布.

式中：λe是电极导热率，W／（m·K）；T是电极温度，K；ρe是电极密度，kg／m3；Cp，e是电极比热容，J／（kg·K）；U是电极熔化速率，m／s；hs是电极与渣池之间对流换热系数，W／（m2·K）；R是电极半径，m；Ts是渣池温度，K.

将渣池传递至电极的总热流密度qslag分为显热热流qsensible和潜热热流qlatent［14-15］.根据初始假设qsensible＝kqlatent（k是自定义系数）和上一迭代步所得熔化速率，可得到电极端部的温度梯度［16］.更新这一迭代步的显热热流和实际热流，进而得到此迭代步的电极熔化速率，直至｜qsensible／qlatentk｜／k≤0.01%.

1.3.3 新电极加热阶段的边界条件

会聚研究与其他描述多学科研究的概念相关联，如跨学科和交叉学科等，但与之不同的是，会聚研究并不是简单地进行多学科交流沟通，而是在多种学科不同研究方式的相互作用影响下，将各类截然不同的研究方法整合成统一的整体以培育新的范式或领域，从而对科学领域的组织分类带来全新变革，为科学和技术进步创造新的途径和机会[4]。会聚研究的基本特征如下：

在新电极加热阶段，新电极温度较低，不会立刻熔化，上述电极熔化速率边界不再适用.为探讨此时的热量传递，提出了新电极端部热流密度的计算方法.根据能量守恒定律，建立电极的热平衡方程：

式中：h0是电极与周围环境之间的对流换热系数，W／（m2·K）；T0是周围环境的温度，K.

将式（14）以常微分方程形成表达，并使用特征方程法根据已知的电极端部和顶端温度边界条件，求得电极轴向温度分布，进而得到电极端部的温度梯度及热流密度.

2 求解过程

采用商业软件ANSYS-FLUENT 对电渣重熔电极更换过程的电磁场、传热、流动及凝固熔化进行求解.采用谐波法求解麦克斯韦方程组，可得到适用于电渣重熔过程中的磁场输运方程，而求解得到的洛伦兹力和焦耳热可分别作为动量源项和热量源项添加到守恒方程.采用动网格技术能实现铸锭生长，并与电极熔化速率相匹配.图1 示出了电渣重熔系统初始状态的边界条件和网格划分，采用六面体网格.在保证计算精度的前提下，为节约计算资源，采用轴对称模型.在多CPU 集群（24 核，2.10 GHz并行计算）上进行计算，时间步长设置为0.001 s，每步至少执行20 次迭代.求解过程中涉及到的材料特性和工艺参数如表1 和2 所列［17］.

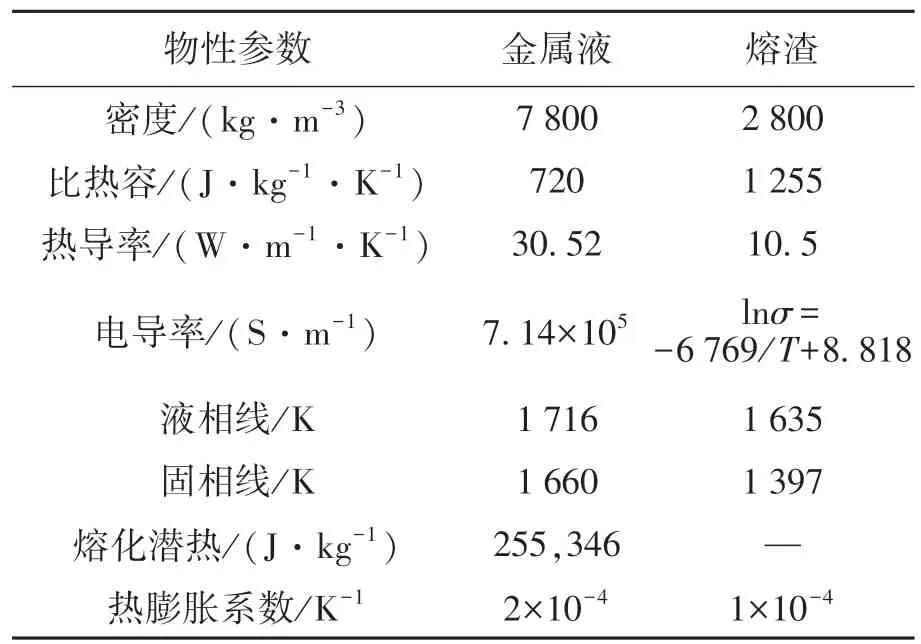
表1 电渣重熔过程的物性参数Table 1 Physical parameters of electroslag remelting process

表2 电渣重熔过程的工艺参数Table 2 Process parameters of electroslag remelting process

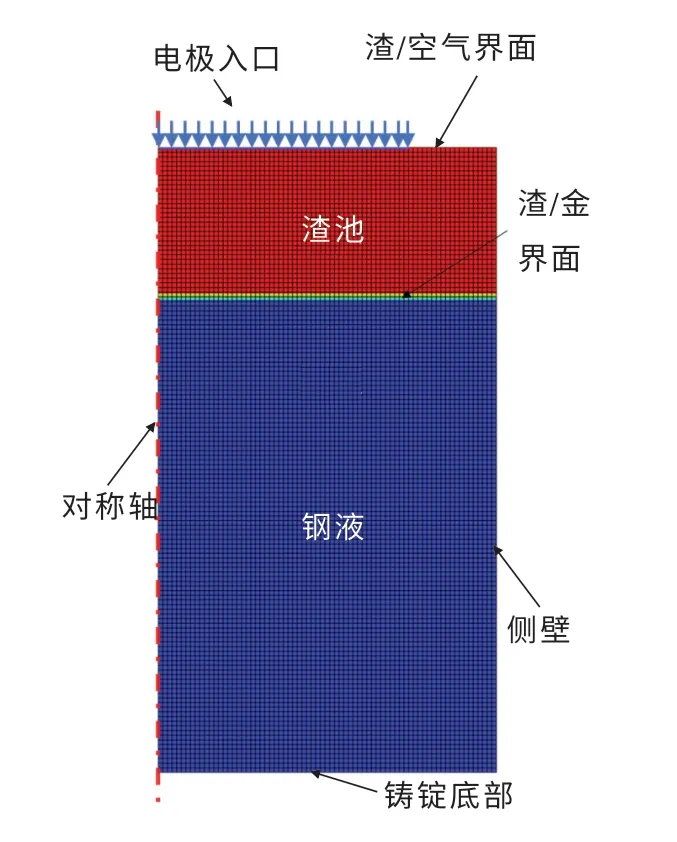
图1 电渣重熔系统初始状态的边界条件和网格划分Fig.1 Boundary conditions and meshing of initial state of electroslag remelting system

3 结果与讨论

3.1 模型验证

实际冶炼过程为模拟提供实验验证，实验采用与模拟相同的操作参数和物性材料（见表1 和2）.电极熔化速率能够反映电渣重熔过程中的流动、传热等特性，故作为模型验证的参照标准.图2展示了在相同操作条件下实验和模拟得到的电极熔化速率对比情况.由图可知，实验得到的电极熔化速率在M0 kg／min 上下波动，与模拟得到的电极熔化速率相对误差为0.15%.误差在允许范围内，模型的可行性得到了验证.出现误差的原因可能是结晶器与熔体绝缘等假设条件，以及材料特性和边界条件的不确定性.

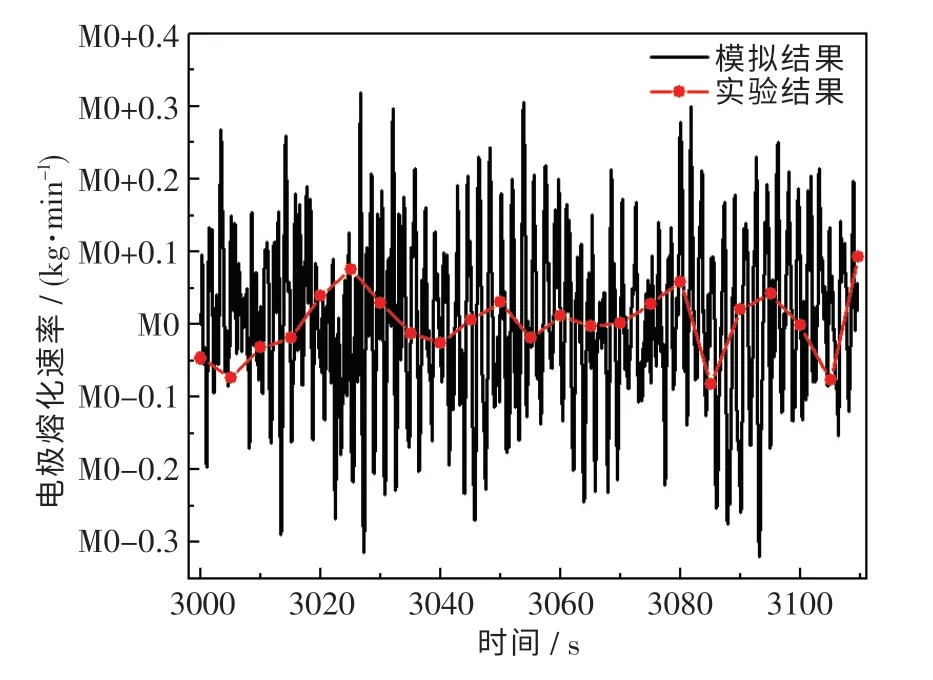
图2 实验和模拟得到的电极熔化速率对比Fig.2 Comparison of electrode melting rates obtained from experiments and simulations

3.2 温度场

图3 展示了电渣重熔电极更换过程的温度场.渣的电阻率远高于钢的电阻率，而焦耳热主要由渣产生，这导致渣池温度明显高于金属液温度.从图3（a）中可看出，渣池内高温区出现在电极端部外侧，此处焦耳热值也最大.渣池内产生的焦耳热主要用于加热和熔化电极，故靠近电极端部的温度较低.由图3（b）～（d）可知，该阶段原电极脱离，热源消失，渣池内储存的热量通过渣池顶部和结晶器壁被大气和冷却水带走，渣池温度逐渐下降.在新电极加热阶段，新电极插入渣池内，热源恢复.在新电极插入渣池瞬间，靠近电极端部附近的温度迅速下降，如图3（e）所示.焦耳热最大值依旧出现在电极端部外侧，渣池内温度从此处开始升高，如图3（f）所示.

图4 展示了原电极脱离阶段和新电极加热阶段电渣重熔过程渣池最高温度的变化.由图可知：随着原电极脱离时间由0 增至110 s，渣池最高温度从1 865 K降低至1 740 K；新电极加热至25 s 时开始熔化，随着新电极加热时间由0 增至25 s，渣池最高温度从1 740 K升高至1 940 K.还可以观察到，新电极加热阶段的后期渣池最高温度高于原电极稳定熔炼阶段.其原因是在新电极加热阶段，电极并没有熔化滴落，但是在原电极稳定熔炼阶段有液滴滴落，液滴温度相对较低，导致渣池内温度略有降低.同时，因为新电极加热阶段电极无液滴滴落，渣池内热量传递没有原电极稳定熔炼阶段那么剧烈，热量更容易聚集，高温区温度也更高.

3.3 流场

图5 展示了电渣重熔电极更换过程的流场.在原电极稳定熔炼阶段，电极受热熔化后，端部会形成一层薄薄的液膜，其在指向渣池中心的洛伦兹力作用下向中心移动，并以液滴的形式滴落，在渣池内形成逆时针的流动回路.靠近结晶器的熔渣被冷却水吸收了大量的热，导致温度下降、密度增大，在重力作用下形成顺时针的流动回路.电渣重熔过程中最大速度主要由滴落的液滴产生［见图5（a）］.在原电极脱离阶段，由于原电极脱离，没有电极熔化产生液滴，液滴驱动的逆时针流动回路逐渐被顺时针流动回路取代［见图5（b）～（d）］.在新电极加热阶段，电磁场恢复，在指向渣池中心的洛伦兹力作用下，流场重新产生逆时针流动回路［见图5（e）］.在新电极熔化阶段，新电极熔化重新产生液滴，逆时针流动回路也更加明显［见图5（f）］.

图5 电渣重熔电极更换过程的流场Fig.5 Flow field during electrode change of electroslag remelting

3.4 熔池形状

图6 展示了电渣重熔电极更换过程的液相分布.金属电极在焦耳热的作用下熔化并以液滴的形式滴落，最终在底水箱和结晶器的冷却下凝固.随着铸锭的增大，底水箱的冷却作用减弱，形成典型的“U”型熔池.在原电极脱离阶段，热源消失，熔池轮廓向上增长，渣池在靠近结晶器处形成一层固态渣皮，如图6（b）（c）所示.这是因为新电极的温度低于熔渣的固相线，故在插入渣池瞬间在端部形成一层固态渣壳.此时，热源恢复，电极端部的渣皮从外侧开始熔化，如图6（e）～（f）所示.

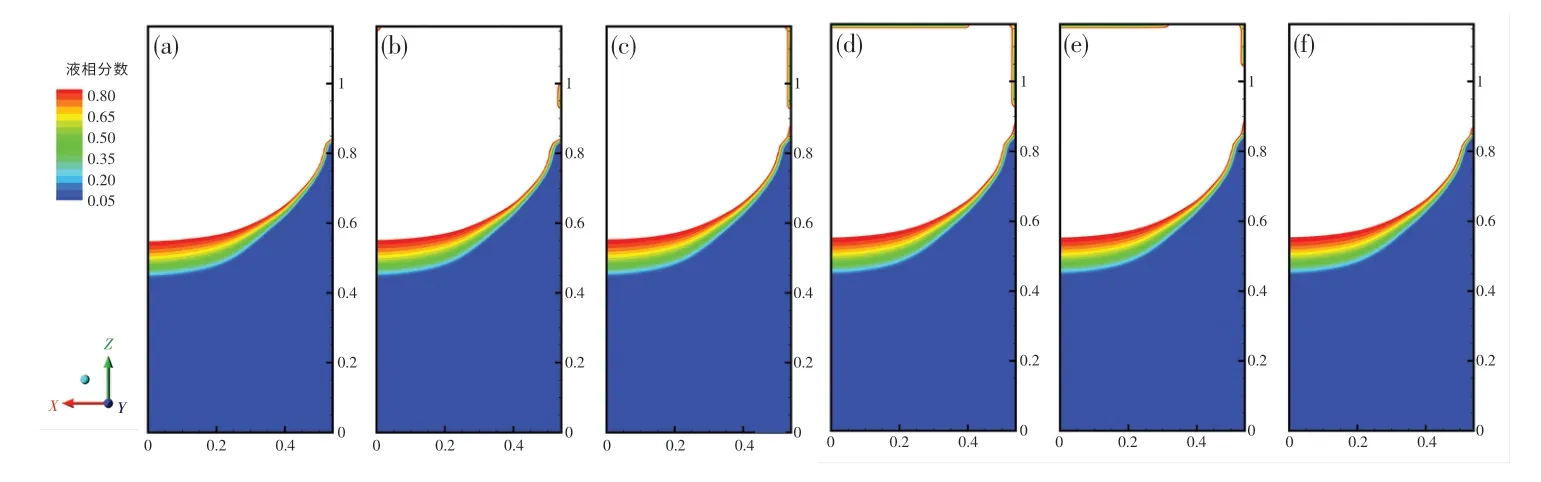
图6 电渣重熔电极更换过程的液相分布Fig.6 Liquid phase distribution during electrode replacement of electroslag remelting

图7 展示了原电极脱离阶段X＝0 和X＝0.54 m处熔池形状沿Z方向的增长率.由图可知，当原电极脱离时间小于95 s 时，中心处熔池轮廓（X＝0）增长率高于靠近结晶器处熔池轮廓（X＝0.54 m）增长率.此时，储存在渣池内的热量仍然可以抵抗结晶器的冷却作用，使得X＝0.54 m 处熔池轮廓没有明显增长.然而，此处熔池轮廓在80s 后陡增，可以推测储存在渣池内热量的消耗达到了“临界值”，储存的热量开始不足以抵抗结晶器的冷却作用.

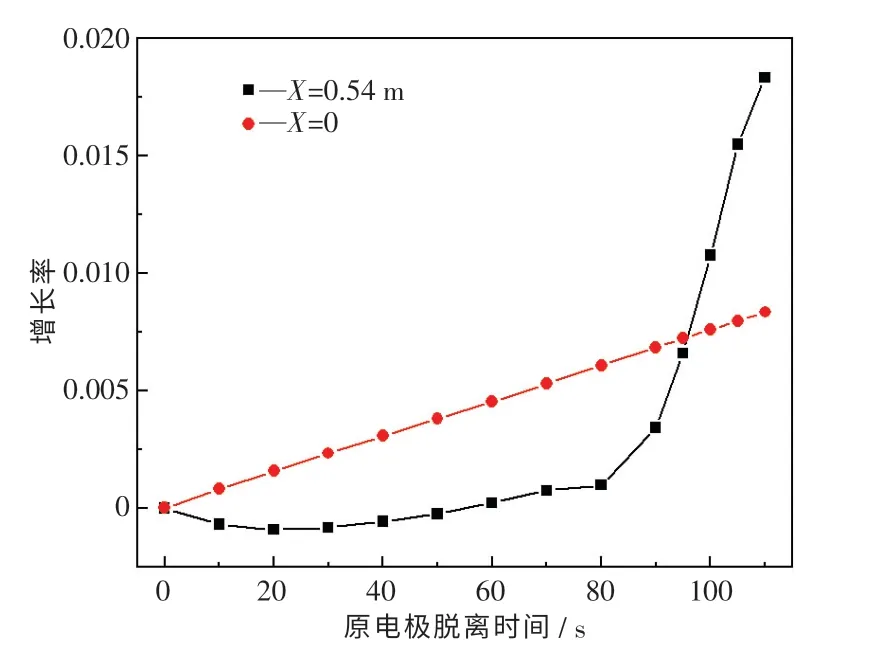
图7 原电极脱离阶段X＝0 和X＝0.54 m 处熔池形状沿Z 方向的增长率Fig.7 Growth rate of molten pool shape along Z direction at X＝0 and X＝0.54 m of primary electrode detachment stage

图8 展示了原电极脱离阶段渣池内熔渣的凝固质量随时间的变化.由图可知：当原电极脱离64 s时，熔渣开始凝固；当原电极脱离110 s 时，凝固渣质量为4.76 kg，其体积占渣池体积的0.46%；原电极脱离180 s 后，熔渣凝固速率明显增快.综上可知，原电极脱离时间应尽量控制在180 s.

图8 原电极脱离阶段渣池内熔渣的凝固质量Fig.8 Solidification quality of slag in slag pool during primary electrode separation

3.5 凝固渣的形成

在新电极加热阶段，新电极的温度低于熔渣的固相线，其插入渣池的瞬间会在端部形成一层固态渣皮，这将影响电渣重熔过程的稳定性，故需要预热处理新电极.图9 展示了不同预热温度下电极沿中心轴方向的温度分布.由图可知，预热温度越低，恢复稳定状态需要的热量越多.

图9 预热电极温度分布Fig.9 Temperature distribution of preheating electrode

图10 展示了不同预热温度下电极端部熔渣凝固质量随时间的变化.从图10 中看出：当预热温度为573，873 K 时，电极端部凝固渣质量在短时间内增大，最大值分别为29.24，24.38 kg，之后凝固渣逐渐熔化；当预热温度为1 173 K 时，熔渣的凝固质量为19.65 kg；随着预热温度从573 K提高到1 173 K，凝固渣完全熔化时间从32 s 降至11 s.

图10 电极端部凝固渣质量随时间变化Fig.10 Change of solidified slag quality at electrode tip with time

4 结 论

（1）在原电极脱离阶段，热源消失，随着原电极脱离时间由0 增至110 s，渣池最高温度从1 865 K降低至1 740 K.新电极加热阶段，热源恢复，随着新电极加热时间由0 增至25 s，渣池最高温度从1 740 K 升高至1 940 K.

（2）在原电极脱离阶段，由结晶器冷却水吸收热量造成的顺时针流动回路逐渐取代由液滴滴落造成的逆时针流动回路.随着新电极插入，逆时针流动回路逐渐明显.

（3）当原电极脱离时间小于95 s 时，熔池轮廓的增长率在中心处（X＝0）高于靠近结晶器处（X＝0.54 m）.X＝0.54 m 处熔池轮廓在80 s 后陡增，可以推测储存在渣池内的热量消耗达到了“临界值”.原电极脱离64 s 后，靠近结晶器的熔渣开始凝固.当原电极脱离110 s 时，凝固渣质量为4.76 kg，占渣池体积0.46%.

（4）随着新电极预热温度从573 K 提高到1 173 K，熔渣的凝固质量从29.24 kg 降低至19.65 kg，凝固渣完全熔化时间从32 s 降低至11 s.