基于基片集成波导加载开口环的介电测量传感器*

赵文强，武鑫磊，景辉辉，陆 畅，张斌珍，段俊萍

（中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051）

0 引 言

介电常数作为反映材料极化性质的指标，是进行微波射频电路设计时的重要参数，一直以来受到国内外学者的广泛关注［1，2］。对材料进行介电常数表征的方式有很多，在微波和射频频段内可以总结为谐振法和非谐振法［3］。谐振法主要包括介质谐振法、开放式谐振法、谐振腔法。由于谐振腔法和其他类型谐振法相比，设计加工简单和测试更加便捷，近年来倍受研究者的关注。文献［4 ～6］分别采用了非谐振法中的射频电路法、传输线法和自由空间法对介质的介电常数进行测量。谐振法和非谐振法相比，不能进行宽频带范围内的测量，但谐振法拥有更高的测量精确度［7］。通常情况下只需要知道某一频点的材料特性，所以谐振法是对材料介电常数进行测量的重要手段。

为了让传感器精度更高的同时体积更小，学者们逐渐采用基片集成波导（substrate integrated waveguide，SIW）代替传统波导，同时在SIW 的基础上努力实现小型化。2020年，蔡本晓等人基于等效磁切壁法获得了小体积的半模SIW（half mode SIW，HMSIW）［8］。虽然这种方法实现了器件的小型化，但随着SIW 的多次切割，对工艺的要求也逐渐提高。2021 年，Xiang Y H 等人采用多层结构实现SIW的小型化，但这种方法结构复杂，加工成本高［9］。2020年，Song X Y等人通过在SIW结构表面加载曲折槽实现小型化［10］。这种小型化方式简单、效果明显、加工成本低，受到越来越多的研究人员的关注。

本文采用SIW 传感器对介电常数进行测量。首先介绍了SIW传感器的基本结构，对该传感器进行介电常数测量的可行性进行了理论分析。通过高频结构仿真器（high frequency structure simulator，HFSS）对传感器进行仿真优化，分析不同介电常数对谐振频率的影响，建立相对频率偏移量和介电常数的关系式，最后进行了实验验证。

1 传感器的设计

设计了一种基于SIW的小型化介电常数测量传感器，具体结构可以分为3 层，上、下两层是金属层，中间层采用聚四氟乙烯（F4B）板材作为介质基板，将传感器四周加入金属化通孔用于防止能量泄漏，传感器的电场最强处作为待测区域。基本结构如图1所示。

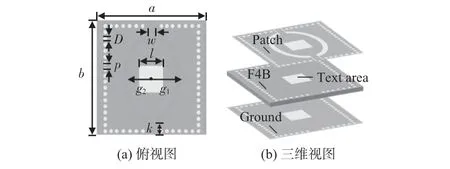
图1 传感器结构

在未刻蚀开口环之前，传感器的截止频率与自身的尺寸以及中间介质基板的介电常数有关。通过在传感器上刻蚀开口环可以降低传感器的工作频率，实现器件小型化。小型化后的传感器工作频率与开口环的尺寸有关。测量时，将物体放入到传感器的待测区域，通过检测传感器的S参数变化计算出材料的各种特性。

将图1的传感器结构模型放入HFSS 中进行仿真分析。该传感器选用F4B 板材作为介质基板，介电常数为2.65，损耗角正切值为0.001 5，板材的厚度为0.8 mm。为了尽可能地实现传感器的小型化，对刻蚀的开口谐振结构进行参数优化，使得传感器的空载谐振频率从3 GHz 降低至1.4 GHz 左右。经过HFSS 仿真优化后的结构参数由表1给出。

表1 传感器设计参数 mm

图2为传感器小型化前后的S11参数对比。由图2 可知，在传感器上刻蚀开口环之后，传感器的空载工作频率从3.0 GHz降低到1.4 GHz左右，实现了对器件的小型化设计。

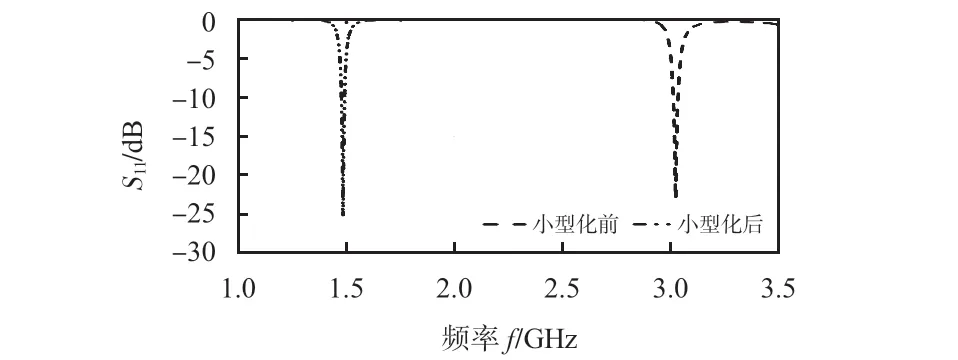
图2 传感器小型化前后的S11参数对比

同时，小型化前、后传感器的电场分布如图3（a）、（b）。不难发现，在相同条件下，刻蚀了椭圆开口环的传感器拥有更加集中的电场分布，并提高传感器的灵敏度。

图3 传感器电场分布

2 工作原理与仿真分析

2.1 等效电路分析

传感器的工作频率可直接反映出待测物体的介电常数。为了分析待测物体的介电常数和传感器工作频率之间的关系，这里采用等效电路的分析方法对传感器的工作原理进行简单的说明。图4（a）为传感器的等效电路模型，图4（b）为传感器等效电路模型简化后的简单LC回路。

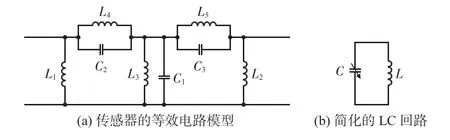
图4 传感器等效电路

在图4（a）中，L1和L2为传感器中的金属化通孔的等效电感，C1为上、下层金属板之间的板间电容。L3为上、下金属板之间的电感，除此之外，C2、C3和L4、L5分别为SIW和谐振结构之间产生的电容和电感。将图4（a）简化为图4（b）时，传感器的工作频率可以表示为f ＝1／2π，L为传感器的等效电感，C 为传感器的等效电容。由于传感器的电感取决于传感器的尺寸以及刻蚀的开口环，因此设计好的传感器，电感L基本不变。传感器频率的偏移来自传感器等效电容的变化。等效电容的变化主要来自于待测区域的上、下层金属板之间的板间电容的影响。待测区域的板间电容的表达式为Cu＝ε0εrA／d，其中，Cu为上下极板之间的板间电容，ε0和εr分别为真空的相对介电常数和上、下极板之间物体的介电常数，A 为导体面积，d 为上层金属板和下层金属板之间的间距。

由上述公式可得出，待测物体的介电常数的大小将直接影响待测区域的板间电容，从而对传感器的频率产生影响。因此，介电常数和传感器的频率之间存在明确的数学关系，具体的关系可以通过仿真数据拟合得到。

2.2 传感器的仿真分析

设置待测物体的介电常数1 ～10 间变化，损耗角正切值固定在0.005。不同的介电常数下仿真结果如图5（a）所示。设置介电常数实部为1，改变介电常数的虚部，使得损耗角正切值从0.01 增大到0.04，仿真结果如图5（b）所示。

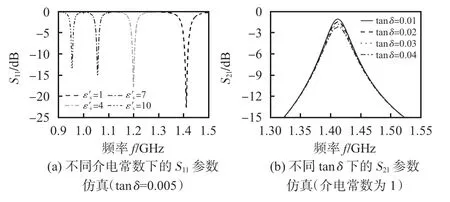
图5 传感器仿真的S参数对比

从图5（a）中可以看出，传感器的频率随着介电常数的增加而降低，同时，随着待测物体介电常数的增加，频率偏移量逐渐减小。由图5（b）可知，介电常数虚部的变化只是改变了传感器的损耗。当待测物体介电常数虚部的增大时，传感器的品质因数降低，对频率基本没有影响。

待测物体的介电常数从1至10变化的过程中，传感器的频率从1.411 GHz偏移到0.954 GHz，频率偏转量达到了457 MHz，相对偏移率为32.4%。数据表明：该传感器对介电常数的变化十分敏感，可以采用该传感器对待测物体的介电常数进行高精度的测量。

考虑到传感器加工时使用的板材参数存在误差，以及实际加工测试过程中不可避免的外界环境对测试结果的干扰，传感器实物会存在频率偏移。本文根据传感器的相对频率偏移量与介电常数之间的关系来拟合出多项式，相对频率偏移量可通过下式计算［11］

式中 fref为测量介质为空气时的谐振频率，f 为测量其他介质时的谐振频率。

对图5中的仿真数据进行处理，得到拟合曲线所需要的相对频率偏移量，拟合出的相对频率偏移量和介电常数的曲线如图6所示，3次多项式拟合结果如式（2）

图6 相对频率偏移量与介电常数的关系曲线

在实验测量结束之后，根据测量得到的频率值计算出各个待测物体的相对频率偏移量，将相对频率偏移量代入到式（2）中便可求得待测物体的介电常数。

3 实验结果

测试时，通过2根线缆将传感器的2 个端口与网络分析仪连接从而检测出传感器的S参数，传感器的实际测试如图7。

图7 传感器测试

测量开始之前，首先要对网络分析仪进行校准，减小系统误差对测试结果造成的影响。在进行介电常数的测量时，将事先准备好的待测物体放入待测区域，并用铜胶带将待测区域覆盖。这样可以让电场更好地渗透到传感器的待测区域，提高传感器的灵敏度。将测量得到的传感器频率转换成需要的相对频率偏移量代入式（2），得到介电常数的测量结果，具体测量结果如表2所示。

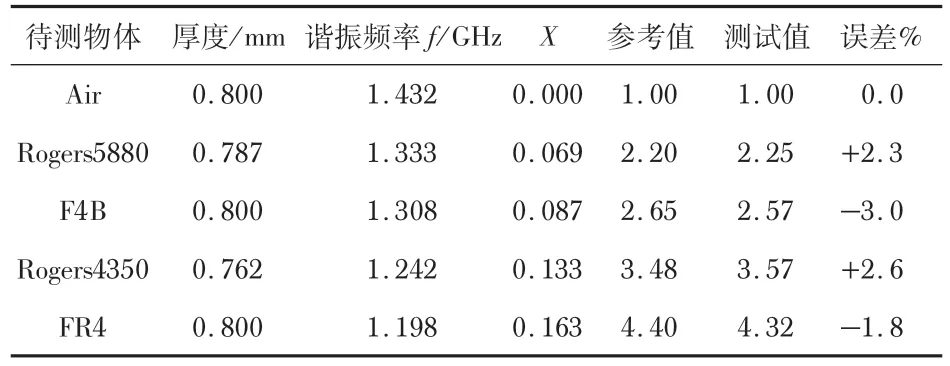
表2 介电常数的测量结果

由表2可知，传感器的测量误差小于3%。考虑到待测物体和待测区域的尺寸存在偏差，这是传感器测量误差的主要来源。

由2.1节中给出的传感器工作频率和待测极板间电容求解公式可知，当待测物体的厚度小于介质基板的厚度时，求得的待测物体介电常数偏大；当待测物体的边长小于待测区域的边长时，求得的待测物体介电常数偏小。

从归一化灵敏度的角度将设计的传感器与类似传感器进行比较［12］。归一化灵敏度表达式如下

式中 S为传感器的归一化灵敏度，Δε′为传感器的测量范围，f1和f2分别为该传感器测量范围内频率变化的上、下限，Δf为传感器测量范围内的频率偏移量。将设计的传感器与同类比较，具体结果如表3。

表3 传感器性能参数对比

4 结 论

本文基于微扰理论，提出了一种新型的小型化介电常数测量传感器。以SIW作为主要结构，设计了椭圆形的开口环刻蚀在传感器表面。椭圆形开口环的引入，集中了电场分布、延长了电流路径并降低了传感器的工作频率，实现了器件的小型化设计。通过HFSS仿真数据拟合出介电常数和传感器工作频率之间的关系式，对多组具有不同介电常数的待测物体进行了测试。实际的测试结果表明，设计的传感器对待测物体的介电常数测量误差小于3%，这说明了传感器性能稳定，可以对待测物体的介电常数进行准确测量。