THE ENERGY CONSERVATION OF THELANDAU-LIFSHITZ-BLOCH EQUATION*

Qiuju XU (许秋菊)School of Mathematicadl Sciences,Chongqing Normal University，Chongqing 40004"1，ChinaE-mail : smlynice@163.com

Huaqiao WANG(王华桥)†College of Mathematics and Statistics，Chongqing University，Chongqing 401331，China E-mail: wanghuaqiao@cqu.edu.cn

1 Introduction

The micromagnetic technique based on the Landau-Lifshitz-Gilbert (LLG for short) equation[29,33,36](see also[3,7,8,30]),or the Landau-Lifshitz(LL for short)equation[1,11,16],can well describe the micro-nano scale magnetic thin film system at low temperatures, and can show the magnetic domain structure and the dynamic evolution of magnetic moments at zero temperature (or low temperatures).However, these micromagnetic equations cannot correctly describe the behavior of magnetodynamics at high temperatures (especially near the Curie temperature of material).A typical example is the ultra-fast demagnetization caused by pulse laser irradiation of a magnetic thin film and the subsequent magnetic recovery process.In this process, the irradiation of the high-energy pulsed laser causes the sample to rapidly heat up locally, and the temperature of the electrons near the irradiation spot is rapidly heated to near the Curie temperature of the magnetic material, so that the region of the film irradiated by the laser light is partially or completely demagnetized in an ultrafast time from several tens of femtoseconds to a few picoseconds,and then,as the heat is diffused,the demagnetization region recovers the magnetism in a period from few hundred picoseconds to a few nanoseconds.Physically, this ultra-fast magnetic response process involves complex interactions between photons,electrons, phonons and magnetons (or magnetic moments).This goes beyond the scope of the classical theory of traditional micromagnetism, and requires the introduction of the deep theory of quantum effect.Moreover, when the temperature is close to the Curie temperature, the magnetization vector of the magnetic moment of the thin film unit is no longer only a change of direction, and its amplitude will also change greatly, so the microscopic description of the traditional LLG equation or the LL equation is completely invalid.On account of this,Garanin[27, 28] proposed the Landau-Lifshitz-Bloch (LLB) equation (see also [2, 24, 42]).This model can describe the micromagnetic dynamic behavior at all temperatures(especially near the Curie temperature of material) and is consistent with a large number of experimental results; it can also describe the relaxation process in the radial direction of the magnetization vector.

With the advent of the information age, more and more information needs to be stored.At the same time, the requirements for information storage are getting higher and higher.At present, the LLB equation has been applied as the theoretical basis for data storage such as spin diodes, spin transistors.

Here, we consider the following LLB equation in the three-dimensional whole space:

There are many authors who have considered the analogue of the Onsager conjecture for other equations; for example, [13, 20, 26, 38] for the Euler equations and [35, 45, 46] for incompressible Navier-Stokes equations, [12, 44] for the compressible Navier-Stokes equations,and [4] for general conservation laws.

This rest of paper is organized as follows: in Section 2, we list some preliminaries and state our main result, Theorem 2.2.Section 3 is devoted to proving the main theorem.

2 Preliminaries and the Main Result

In this section, we first introduce some function spaces.We define the function spaces H1(R3)=:H1as follows:

Here, Lp(R3) =: Lp, p > 0 stands for pth-power Lebesgue integrable function spaces defined in R3and taking values in R3.Similarly, we can define the function spaces H2(R3)=:H2.In this paper, 〈·,·〉 denotes a scalar product in a Hilbert space L2.First, we give the result of the global existence of weak solutions to (1.1)–(1.2).

Theorem 2.1 Assume that m0(x) ∈H1(R3).For a given T > 0, there exists a weak solution m(t,x) of (1.1)–(1.2) such that (1.1) holds in the sense of distributions on (0,T)×R3and the solution satisfies the energy inequality

Proof The method of proof is standard, so we omit the details.For additional details,see [34] (global existence of weak solutions in a bounded domain) and [15] (a standard domain expansion).□

3 Proof of Theorem 2.2

For the terms J1and J2, since m,∇m ∈L2(0,T;L2(R3)) (see (2.1)), by employing the properties of a mollifier, we can easily get that

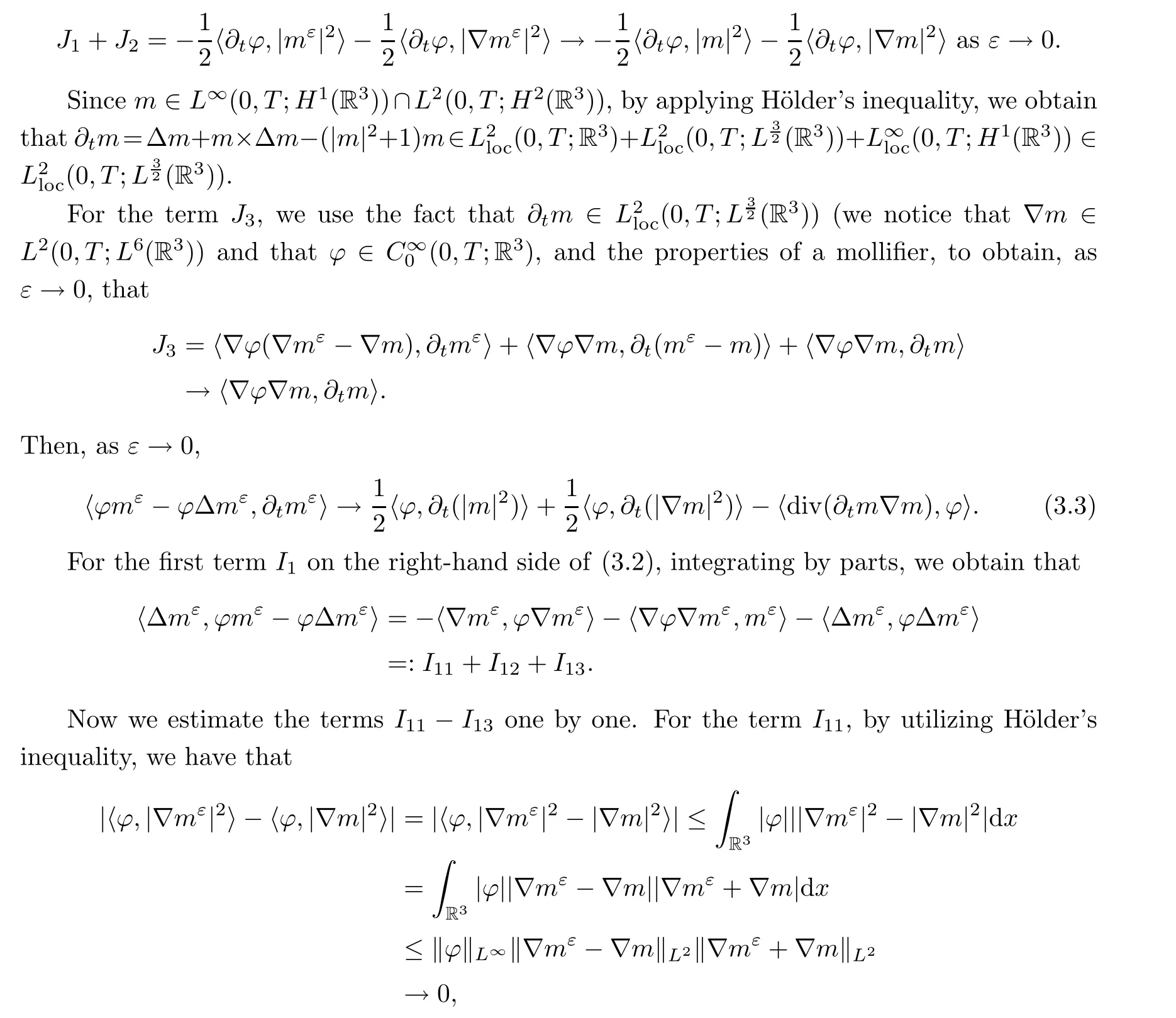
since ‖∇m‖L2≤C and ‖∇mε-∇m‖L2→0 as ε →0.

For the term I12,by the properties of the mollifier and the fact that ∇m,m ∈L2(0,T;L2(R3)),we can easily obtain that

Note that

Therefore, we get that

Similarly, we obtain that

Hence, one deduces that, as ε →0,

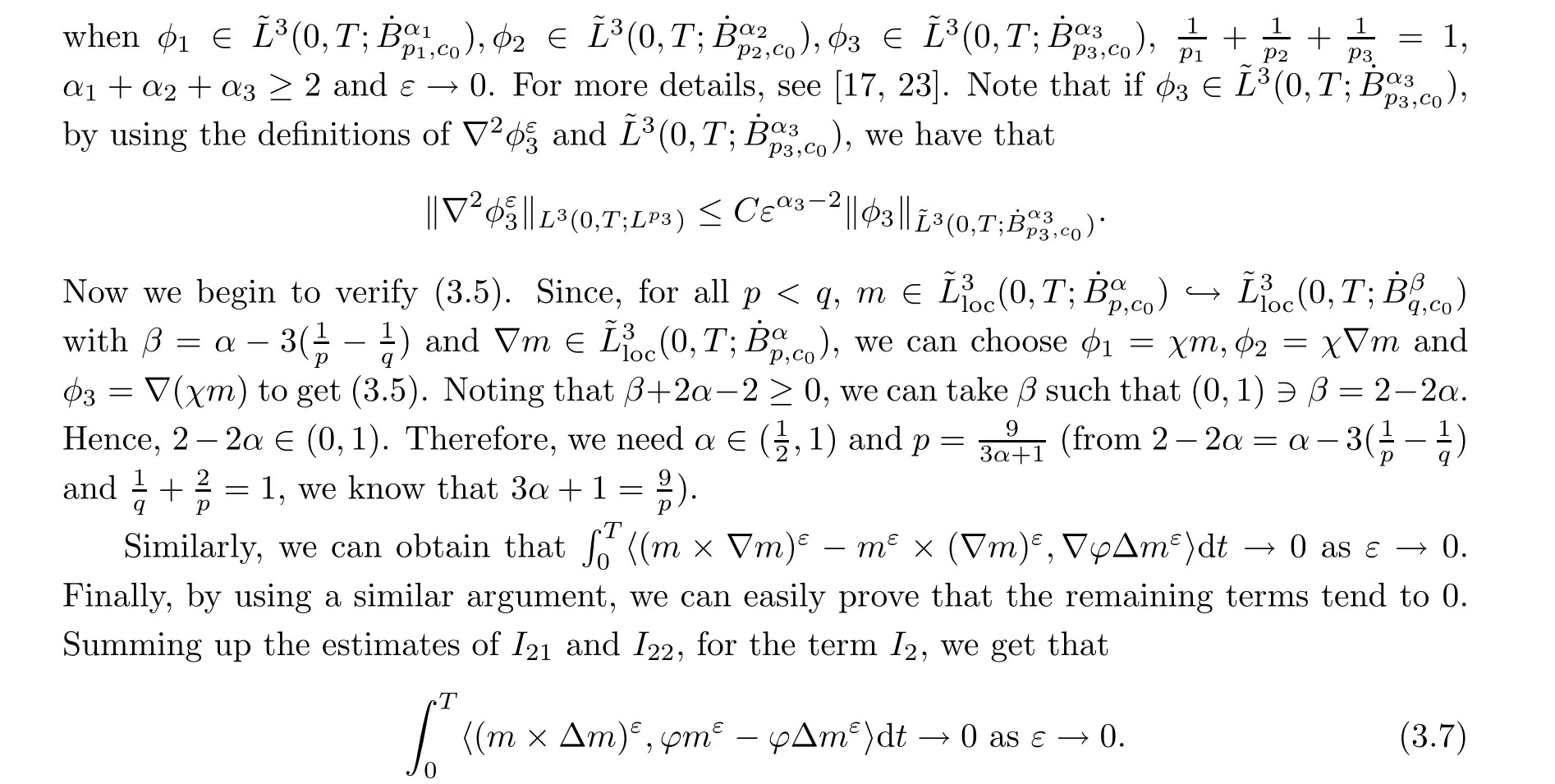
Now we deal with the term I3= -〈(|m|2m)ε,ϕmε〉 + 〈(|m|2m)ε,ϕ∆mε〉- 〈mε,ϕmε-ϕ∆mε〉=:I31+I32+I33.First, we can rewrite the term I31as

For the first term on the right-hand side of (3.8), applying Hölder’s inequality, the Sobolev embedding inequality and (2.1) implies that

Hence, using the fact that ∆m ∈L2(0,T;L2(R3)), we obtain, as ε →0, that

Conflict of InterestThe authors declare no conflict of interest.