LARGE DEVIATIONS FOR TOP EIGENVALUES OF 3-J ACOBI ENSEMBLES AT SCALING TEMPERATURES*
2024-01-12LiangzhenLEI雷良贞SchoolofMathematicalScienceCapitalNormalUniversityBeijing100048Chinamailleiliangzhencnueducn
Liangzhen LEI (雷良贞)School of Mathematical Science,Capital Normal University,Beijing 100048,China E-mail : leiliangzhen@cnu.edu.cn
Yutao MA(马宇韬)+School of Mathematical Sciences & Laboratory of Mathematics and Complea Systems of Ministry of Education,,Beijing Normal University,Beijing 100875,China E-mail: mayt@bnu.edu.cn
1 Introduction

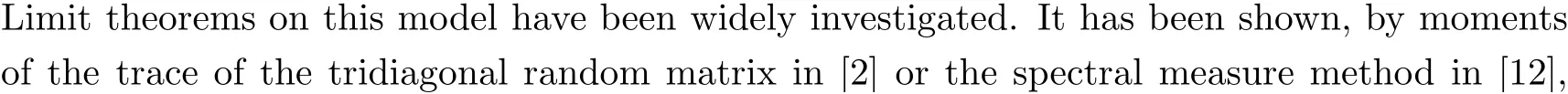

For γ >0, we get another large deviation.


The rest of this paper is organized as follows: Section 2 is devoted to the proof of Theorem 1.1 and we prove Theorem 1.2 in Section 3.Appendix focuses on some lemmas.
2 Proof of Theorem 1.1

For simplicity, set Xi= pλi/p1for 1 ≤i ≤n.We now give the joint density function of(X1,··· ,Xn).


2.1 The Verification of (2.1)

The limit (2.1) is verified.
2.2 The Verification of (2.2)
For any x ∈(0,1), on the set {X(n)≤x} we know

since X(n)≥0.The proof of the limit (2.2) is complete.
2.3 The Verification of (2.3)
If x<1,the limit(2.3)holds automatically,since Jσ(x)=-∞,and Jσ(x)=0 if and only if x=1.By Theorem 2 in[9], X(n)converges almost surely to 1, which completes the case x=1.
Now we suppose that x>1.Since G is open, we choose r,a,b such that 1 As for Theorem 1.1, we just verify Theorem 1.2 for σ > 0, and it is enough to take the limit when σ = 0.For the large deviation principle of X(n), we need to prove the weak large deviation principle of X(n)and the exponential tightness.As in [11], we are going to check the following three limits: for weak large deviation and for the exponential tightness. Based on this theorem, following the standard argument, as in [1] and[11], we are going to check the limits (3.1)–(3.4). For all x By the large deviation principle for Ln, we have that This immediately implies (3.3). Recall that u2 Starting from (3.4), it remains to prove that on the condition that 0 ≤xn≤M and that supp (Ln-1) ⊂[0,M] for n large enough under the condition A.By the large deviation principle for Ln-1, Lemma A.2 and the boundedness of φM, the second term in the above bound can be neglected.Therefore, we have that Here, for the last equality, we use the continuity of The verifications(3.1),(3.2),(3.3)and(3.4)are all done now and the proof of the large deviation is complete. Conflict of InterestThe authors declare no conflict of interest. Appendix
3 Proof of Theorem 1.2

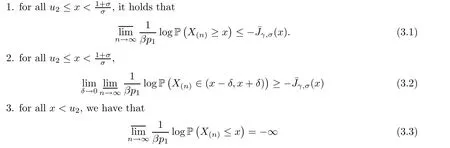

3.1 The Verification of (3.3)

3.2 The Verification of (3.4)
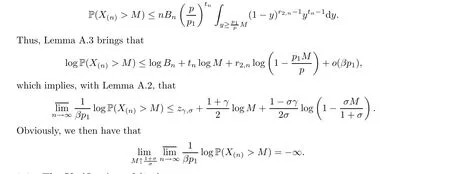
3.3 The Verification of (3.1)




3.4 The Verification of (3.2)
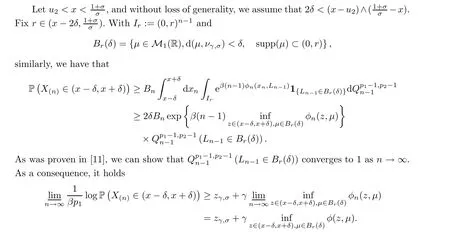
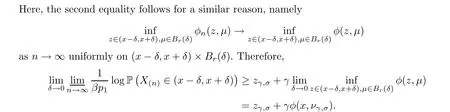

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- NATURALLY REDUCTIVE (Q1, a2)METRICS*
- BLOW-UP SOLUTIONS OF TWo-COUPLEDNONLINEAR SCHRODINGER EQUATIONS IN THE RADIAL CASE*
- THE ENERGY CONSERVATION OF THELANDAU-LIFSHITZ-BLOCH EQUATION*
- MULTIPLE POSITIVE SOLUTIONS TO A CLASSOF MODIFIED NONLINEAR SCHRODINGER EQUATION IIN A HIGH DIMENSION*
- DISTORTION THEOREMS FOR CLASSES OFg-PARAMETRIC STARLIKE MAPPINGS OF REAL ORDER IN Cn*
- BOUNDEDNESS AND COMPACTNESS FOR THE COMMUTATOR OF THE w-TYPECALDERON-ZYGMUND OPERATOR ON LORENTZ SPACE*
