MULTIPLE POSITIVE SOLUTIONS TO A CLASSOF MODIFIED NONLINEAR SCHRODINGER EQUATION IIN A HIGH DIMENSION*
2024-01-12YanshengZHONG钟延生YongqingLI李永青SchoolofMathematicsandStatisticsFJKLMAACenterforAppliedMathematicsofFujianProvinceFJNUFujianNormalUnioversityFuzhou350117Chinamailzys08fjnueducnyqlifjnueducn
Yansheng ZHONG(钟延生)† Yongqing LI (李永青)School of Mathematics and Statistics & FJKLMAA,& Center for Applied Mathematics of Fujian Province (FJNU),Fujian Normal Unioversity,Fuzhou 350117,China E-mail: zys08@fjnu.edu.cn; yqli@fjnu.edu.cn
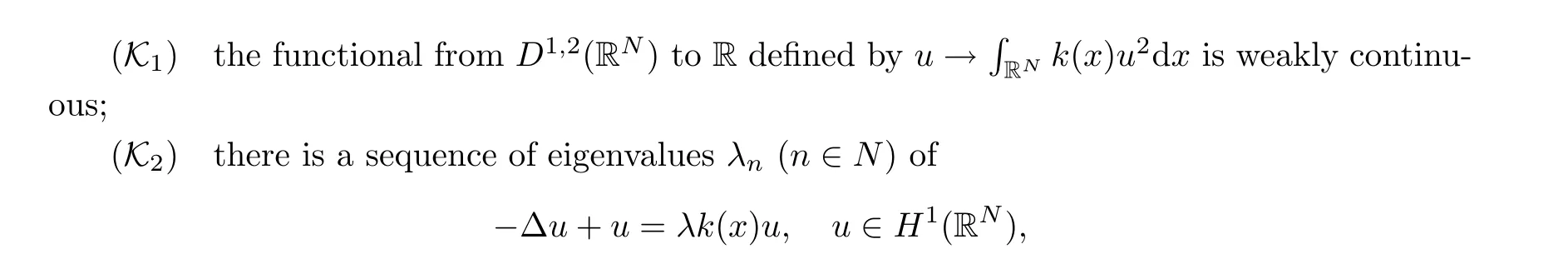
with 0 < λ1< λ2≤λ3≤··· ≤λn≤···, where λn→∞as n →∞.Moreover, λ1is simple and each eigenvalue is of finite multiplicity.The associated normalized eigenvalues are denoted by e1,e2,··· ,en···, with ‖ej‖ =1,j = 1,2···.In particular, the first eigenfunction is e1> 0 in RN.In addition, one has the variational characterization of the sequence

which are derived as models in various branches of mathematical physics, such as in [6–12].Mathematical analysis of the ground states and bounded state solutions of the above equation(∗) has been performed in terms of various variational arguments.For instance, the authors of [13–17] proved the existence of solutions by dual methods, Nehari methods, Orlicz-Sobolev spaces and the approximation method.Some other cases with the additional term v(x)u were discussed in [18–26]; see also the references therein.In addition, the modified term can be regarded as a perturbation to the usual semilinear Schrödinger equation; see [27, 28].The authors in [29, 30] initially set Y ={u|u ∈H1(RN),∫RNu2|Du|2dx<+∞}, and then used the critical point theory for continuous functionals in the metric space Y to obtain the solutions,on the condition that the modified term is uniformly bound.
We here prefer to focus on the typical modified Schrödinger equation (1.1).For the onedimensional case, Chen[1] proved that the additional term 2(|u|2)′′u is helpful for finding positive solutions when the coefficient a(x) of the nonlinearity is sign-changing.By way of proving this, he removed the sign condition∫RNa(x)ep1dx < 0 used to prove the existence of positive solutions for the semilinear elliptic equations (this is also named “a necessary condition”; see[2, 3]).
To the best of our knowledge, the existence of multiple solutions has not been considered for equation(1.1)in high dimensions.It should be noted, however,that in[1], the functional J(given in (2.1)) is well defined on H1(R1), due to the fact that H1(R1) ˛→L∞(R1).However,this is not the case in high dimensions, since H1(RN) ˛→L2∗(RN) as N > 1.Hence, to overcome this difficulty, we will use cut-offtechniques (as in [31]) to reduce the variational setting to one for a C1-functional defined on H1(RN).More specifically,we apply the smoothly truncated functions a(x,s), G(x,s) (given in Section 2) to the modified term “2(∆(|u|2))u”and the polynomical term “a(x)|u|p-2u” in equation (1.1), respectively.On account of the truncation, more delicate analysis than that of [1] is required here.By checking the Palais-Smale condition and the L∞-bounded estimates of solution u to the truncated functional Iλ,M,we present our main results from the local minimum and mountain-pass geometry.
Theorem 1.1 Supposing that (A1), (A2), (K1), (K2) hold and that 4 (i) if 0<λ ≤λ1, then eq.(1.1) has at least a positive solution in H1(RN); (ii) there is a ¯δ > 0 such that, for any λ ∈(λ1,λ1+¯δ], eq.(1.1) has at least two positive solutions on H1(RN). Remark 1.2Here, differently from [31], we deal with the sign-changing coefficient case.For convenience, we study the special modified nonlinear Schrödinger equation, i.e., bij(x,s)=(1+4s2)δi,j.This method may be applied to the general case bij(x,s)generated by the equation(∗). The rest of this paper is organized as follows: in Section 2 we set up the modified functional Iλ,Mand perform an analysis of the (CPS)dsequences of Iλ,M.Section 3 is devoted to establishing the existence of mountain pass and local minimum type solutions to equation(1.1). Throughout the paper,the constants C and Cjare used in various places to denote constants independent of the sequences in the arguments. Define the truncated functional Iλ,M: H1(RN)→R as follows: Hence, for any ϕ ∈H-1(RN), we have that, as n →∞, Here we use compactness embedding (2.5) and Fatou’s Lemma along with the fact that Taking ϕ=(η∊∗v)ζm∈C1(RN)∩H1(RN) in (2.11) with the standard mollifier η∊, it is clear that supp(ϕ)⊂BR(x) for any m ∈N and m>2, and that Here we use (2.14) and the fact that b′M(un)=0 as |un|≥M and p/2-2>0, due to the fact that p > 4.Moreover, (2.16) can be applied to the domain Ω+= {x|x ∈RN, a(x) > 0} by choosing the appropriate testing function ϕ with supp(ϕ)⊂Ω+.It follows first that v =0 a.e.in Ω+.Then, (2.10)and(2.16), with the assumption(A2), give that v(x)=0 a.e.in RN.This finishes the proof of Claim 1.□ We need the next lemma about the property of a bounded(CPS)dsequence.The interested reader is referred to Lemma 3.1 in [31] (we omit the proof here). Lemma 2.5Let {un} ⊂H1(RN) be a (CPS)dsequence.Assume that {un} weakly converges to u in H1(RN).Then u is a solution of (1.6) and un→u in H1loc(RN). Using the approach of Moser and slightly modifying the procedure of proof of Lemma 2.4 in [31], we can estimate the L∞-bound of a critical point of Iλ.Moreover, the estimate is controlled by the value of the functional, and is independent of the parameter M.Hence, for M being large enough, we obtain critical points of the original functional Jλ, or solutions to our problem (1.1). Lemma 2.6Let u be a critical point of Iλ.Then u ∈W1,∞(RN) and ‖u‖W1∞(RN)≤C,where the constant C depends on the value Iλ(u) only, and is independent of M. The following estimate is about the decay of solution u: Lemma 2.7Letting u be a critical point of Iλ, u(x) →0, D(u(x)) →0, exponentially as |x|→∞. With slight modifications, Lemma 5.10 from [15] applies (we omit it here). Now, we give the crucial lemma about the (CPS)dcondition. Lemma 2.8Under the assumptions of Lemma 2.2, for any d ∈R, the functional Iλsatisfies the (CPS)dcondition. ProofLet {un}n∈N⊂H1(RN) be a (CPS)dsequence of the functional Iλ.Lemma 2.2 implies that {un}n∈Nis bounded in H1(RN) uniformly with respect to n ∈N.Going,if necessary, to a subsequence still denoted by {un}n∈N, we have, for each bounded domainΩ ⊂RN, as n →∞, Since the other terms are always nonnegative, it follows that (2.39) holds.Thus the desired result (2.36) of Lemma 2.9 follows. Now, one deduces from (2.35) and (2.36) that Now we define the mountain pass value CJby where ΓJ={g ∈C([0,1], Y)|g(0)=θ, Jλ(g(1))<0}. Similar values are also valid for the functional Iλ, which is dependent on the parameter M.Here, we denote Iλby Iλ,Mclearly, and Therefore we have that By (3.3) and Lemma 2.6, we choose M0such that, for M ≥M0, In what follows, we always assume that M ≥M0, thus, if CMis a critical value of Iλ,M, it is also a critical value of Jλ.Hence, for simplicity, we denote Iλ,Mby Iλin the following. Lemma 3.1Assume that the hypotheses (A1), (A2), (K1), (K2) hold, and that 4 (i) if 0<λ<λ1, u=0 is a local minimizer of Iλ; (ii) there are positive constants ¯δ, ρ and ρ0such that,for any λ ∈[λ1, λ1+¯δ),Iλ|∂Bρ≥ρ0;(iii) there is ¯u ∈H1(RN) with ‖¯u‖>ρ such that Iλ(¯u)<0 for any λ>0. ProofFirst, if 0 < λ < λ1, from the hypothesis and the Sobolev inequality H1(RN) ˛→Lp/2(RN) with 4 where ˜θ is a positive constant depending only on ρ. Indeed, one notes that if then t < ρ, and in particular, the Lebesgue measure of the set A = {x||u(x)| = |te1(x) +v(x)| > M -1} is finite.We can obtain this by following argument: obviously, the set A ={x||u(x)| = |te1(x)+v(x)| > M -1} is equal to A = {x|v(x) > M -1-te1(x) or v(x) <-(M -1)-te1(x)}.Reminding ourselves that t < ρ small enough and ‖e1‖L∞(RN)= C0, we get that M -1-te1(x) ∼M -1 and -(M -1)-te1(x) ∼-(M -1) as M is large enough.Then, combining this with the fact that ‖v‖L2(Ω)<ρ, one can deduce that the measure |A| is finite.Thanks to this result, and noting that b′M(u)= 1 if x ∈RNA, we can estimate (3.12)as follows: Here we use all of the exponents 3µ1,2µ2,µ3,p >4 and ν1,2ν2,2ν3>2, and if ‖u‖H1is small enough, one has that clearly satisfies condition (ii) of Lemma 3.1. Third, we confirm (iii).Since |Ω+| /= 0 and a(x) is continous in RN, by choosing the first eigenvalue function e1, it holds, for any s ≥0, that Thanks to Lemmas 2.8 and 3.1, one can use the mountain passing theorem (see [36]) to obtain the existence of the solution uλ,M.Combining this with the fact that Iλ,M(u) = Iλ,M(|u|),the solution is nonnegative.Then the strong maximum principle implies that the solution is positive.□ Proposition 3.3Let the hypotheses in Lemma 3.1 hold.Then the functional Iλ(given in (2.2)) has another positive solution wλ, with Iλ(wλ)<0 for λ1<λ<λ1+¯δ. ProofSet the closed ball Dρ= {u ∈H1(RN) : ‖u‖ ≤ρ} with ρ defined as in Lemma 3.1.Denote that for R>R2, which implies that Iλ(tηRe1)<0 as t is small enough.Hence, c2,λ<0. In addition, note that Iλ(u)=Iλ(|u|).By applying the Ekeland variational principle [6] to the value c2,λ(see (3.19)), one can prove the existence of another nonnegative solution of the functional Iλ.Then, the strong maximum principle implies that the solution is positive.□ Proof of Theorem 1.1Due to Lemma 2.6, one has the L∞-estimate for the solutions given in Propositions 3.2 and 3.3.Hence, by choosing M large enough in (3.4), one can show the conclusion of Theorem 1.1.□ Conflict of InterestThe authors declare no conflict of interest.2 Palais-Smale Condition to the Modified Functional
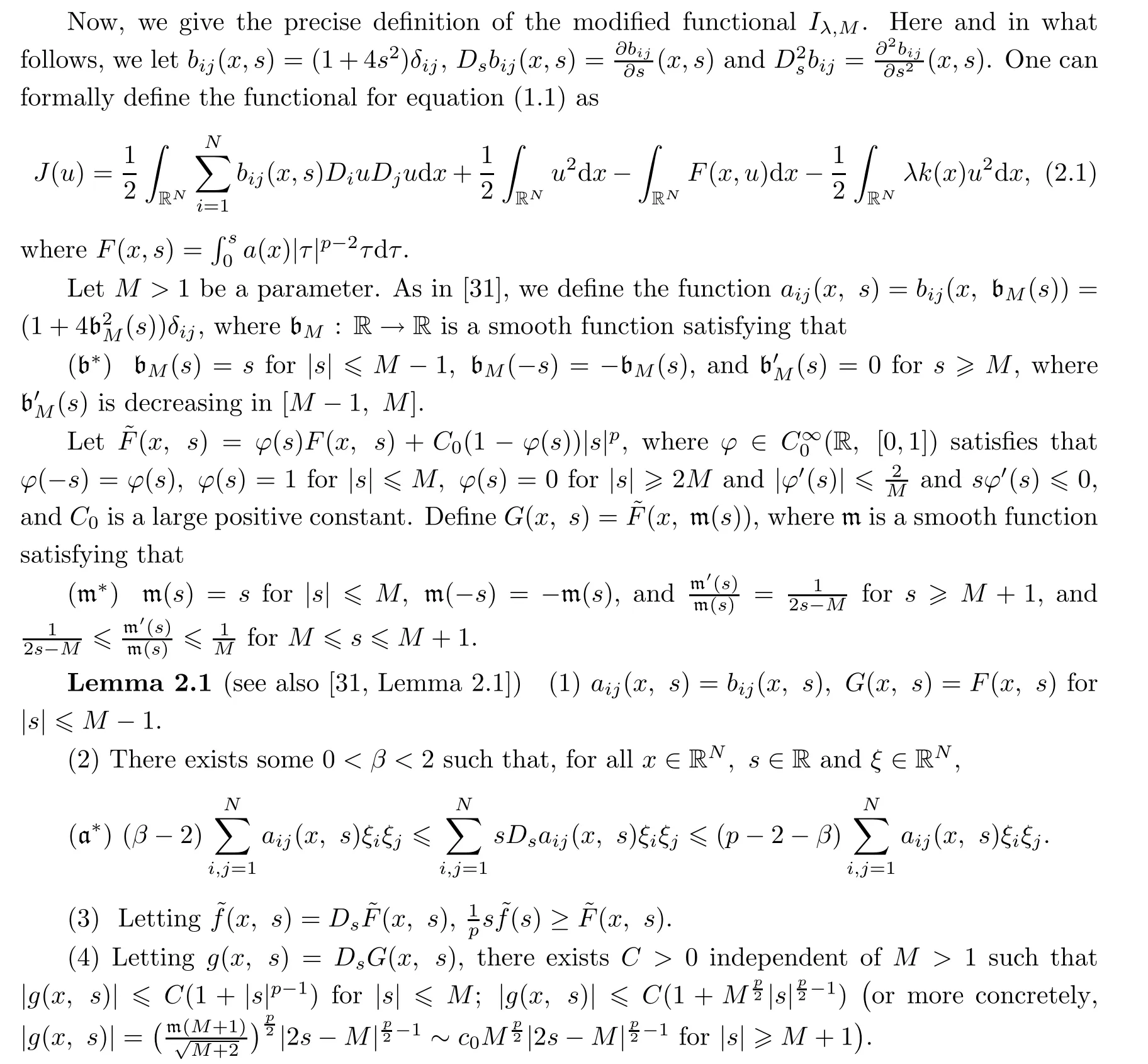



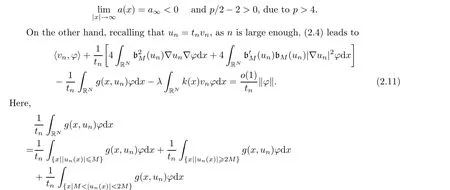











3 Solutions of Local Minimum and Mountain Pass Type



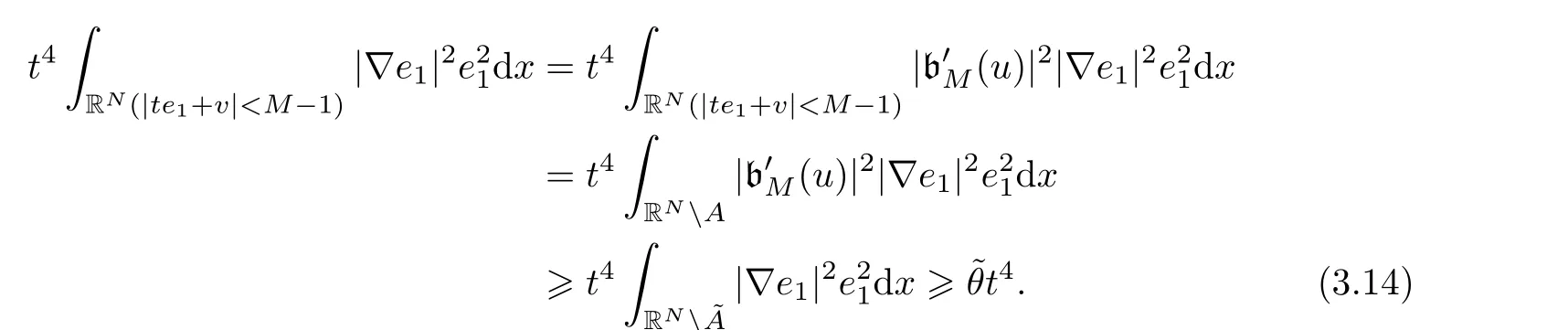





杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- NATURALLY REDUCTIVE (Q1, a2)METRICS*
- BLOW-UP SOLUTIONS OF TWo-COUPLEDNONLINEAR SCHRODINGER EQUATIONS IN THE RADIAL CASE*
- THE ENERGY CONSERVATION OF THELANDAU-LIFSHITZ-BLOCH EQUATION*
- LARGE DEVIATIONS FOR TOP EIGENVALUES OF 3-J ACOBI ENSEMBLES AT SCALING TEMPERATURES*
- DISTORTION THEOREMS FOR CLASSES OFg-PARAMETRIC STARLIKE MAPPINGS OF REAL ORDER IN Cn*
- BOUNDEDNESS AND COMPACTNESS FOR THE COMMUTATOR OF THE w-TYPECALDERON-ZYGMUND OPERATOR ON LORENTZ SPACE*
