BLOW-UP SOLUTIONS OF TWo-COUPLEDNONLINEAR SCHRODINGER EQUATIONS IN THE RADIAL CASE*
2024-01-12QianqianBAI白欠欠SchoolofMathematicsScienceandKeyLaboratoryofSichuanProvinceSichuanNormalUniversityChengdu610068Chinamail1370733971qqcom
Qianqian BAI (白欠欠)School of Mathematics Science and V.C.& V.R.Key Laboratory of Sichuan Province,Sichuan Normal University,Chengdu 610068,China E-mail: 1370733971@qq.com
Xiaoguang LI (李晓光)Li ZHANG(张莉)† V.C.& V.R.Key Laboratory of Sichuan Province,Sichuan Normal University,Chengdu 610068,China E-mail : Liagmath@163.com; lizhang_ hit@163.com


This identity implies that, if E0[u(t)]<0 and∫RN|x|2|u0|2dx<∞, then the solutions blow up in finite time when p > 1+4/N.Since Glassey’s work, research on the existence of blow-up solutions to eq.(1.1) has made great progress (see, for example, [16, 18] and the references therein), based primarily on the finite variance assumption.In order to obtain the blow-up solutions of eq.(1.1)with infinite variance(i.e.,∫RN|x|2|u0|2dx=∞), localized virial identities were established and applied in [3–5, 9, 12, 13].
In this paper, we investigate the Cauchy problem of the following coupled nonlinear Schrödinger equations
Here i is the imaginary unit, (u,v) = (u(t,x),v(t,x)) ∈C×C and (t,x) ∈R×RN, ∆is the Laplace operator on RN, N ≥2, 0 < p < 2/(N -2) (0 < p < ∞, if N = 1,2) and β > 0 is a real constant.
This system arises in nonlinear optics regarding the propagation of polarized laser beams in a birefringent Kerr medium (see [1, 6, 11, 14, 15, 17]).It is worth noting that, when p=1,the nonlinear terms are referred to in terms of Kerr nonlinearity in the physics literature.
According to the ideas of Ginibre and Velo [7], Fanelli and Montefusco [6] showed that the Cauchy problem of system(1.2)is locally well-posed in H1(RN)×H1(RN).The corresponding solution (u,v) of (1.2) also obeys the conservation laws of mass and energy.That is,
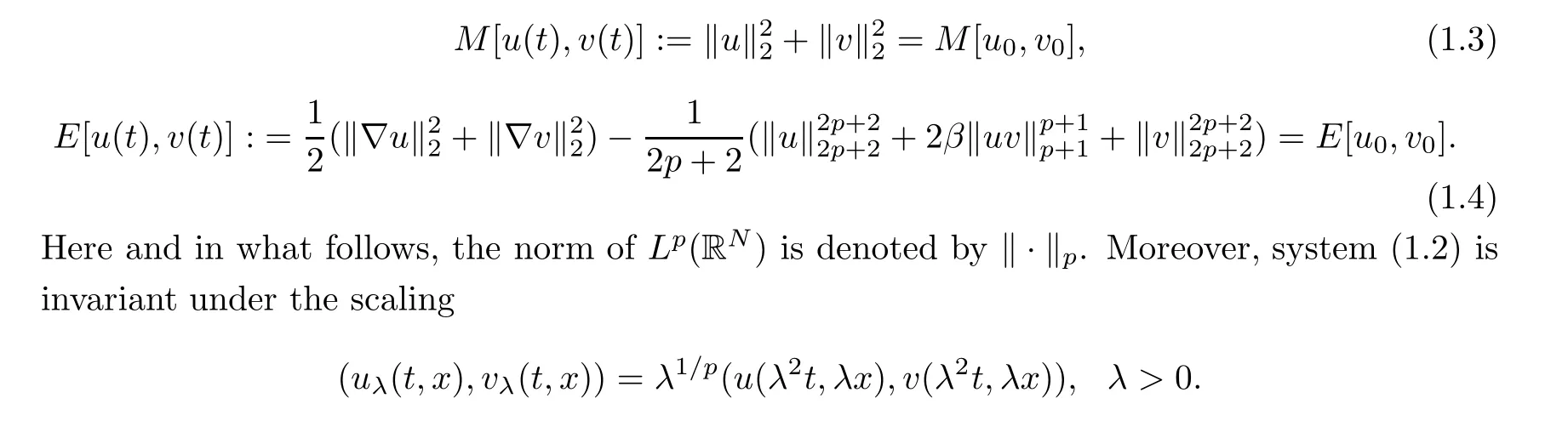
Thus, from this point of view, the critical Sobolev exponent is sc=N/2-1/p, and the ˙Hscnorm is also invariant under this scaling.
Before proceeding, we define the notations
where (Q,R) = (Q(x),R(x)) is the ground state to the following coupled nonlinear elliptic equations associated with (1.2):
For system(1.2), the global existence and blow-up of solutions was studied in[6, 10].More precisely, using the conservation laws (1.3)–(1.4)and the sharp Gagliardo-Nirenberg inequality(2.1),Fanelli and Montefusco[6]proved that the solutions exist globally in each of the following two cases:
(i) 0 (ii) p=2/N and ‖u0‖22+‖v0‖22 a sharp threshold of blow-up for system (1.2) was established by Li and Wu [10] as follows: (i) if p ≥2/N, ∧[u0,v0]<∧[Q,R] and ν[u0,v0]<ν[Q,R], then the solutions exist globally for all time; (ii) if p ≥2/N, (|x|u0,|x|v0) ∈L2(RN)× L2(RN), ∧[u0,v0] < ∧[Q,R] and ν[u0,v0] >ν[Q,R], then the solutions blow up in finite time. As we can see, the proof of [10] for the blow-up solutions was in the framework of finite variance.However,the blow-up of radial solutions for system(1.2)with infinite variance has not been solved yet.Our main purpose in this paper is to prove the existence of blow-up solutions with infinite variance in the radial case.To solve this problem, inspired by the ideas of Ogawa and Tsutsumi [12, 13], we consider the following virial potential Then we obtain our first main result by estimating the localized virial identities. Theorem 1.1Let N ≥2, 2/N ≤p < 2/(N -2) (1 ≤p ≤2 if N = 2), (u0,v0) ∈H1(RN)×H1(RN) be radially symmetric and let E[u0,v0] < 0.Then the blow-up of (1.2)occurs in forward time before T∗, where It is worth noting that the assumption E[u0,v0]<0 is a sufficient condition for the existence of blow-up solutions in finite time, but it is not necessary in Theorem 1.1.This raises a natural question: if E[u0,v0] ≥0, under what conditions do the blow-up solutions exist? Using the idea of establishing the invariant evolution flows of (1.2) from [10], we have our second main result. Theorem 1.2Let N ≥2, 2/N < p < 2/(N - 2) (1 < p ≤2 if N = 2) and let(u0,v0)∈H1(RN)×H1(RN) be radially symmetric.Suppose that Then the solutions (u,v) of (1.2) must blow up in finite time. Remark 1.3As what we have seen, Theorem 1.2 shows that there is no restriction on the initial energy if (1.7)–(1.8) hold.In addition, Theorem 1.2 is no longer valid if p = 2/N,due to the fact that the solutions of (1.2) exist globally if E[u0,v0]≥0. The rest of this paper is organized as follows: we devote Section 2 to listing some useful results which will be needed in what follows.In Section 3, we establish localized radial virial estimates to prove Theorem 1.1.In Section 4, we prove Theorem 1.2 by giving the invariant flows generated by (1.2) and the localized radial virial estimates established in Section 3. In this section, we first recall the local well-posedness of system (1.2) in [6]. Moreover, the above inequality also holds for N ≥3 and s=1. In order to prove the existence of blow-up solutions for system (1.2), we need several lemmas.Let us first define the virial potential Iφ(t): Obviously, Then, we get the following localized radial virial estimates: Lemma 3.2 Let N ≥2, p = 2/N, R > 0, ϕ be as in (3.6) and let (u0,v0) ∈H1(RN)×H1(RN) be radially symmetric.Then, for any ε > 0 and t ∈[0,Tmax), the corresponding solutions (u,v) of (1.2) satisfy Consequently, by substituting (3.13) into (3.11), we obtain (3.8) directly.□ Lemma 3.3 Let N ≥2, 0 0, ϕ be as in (3.6) and let (u0,v0)∈H1(RN)×H1(RN) be radially symmetric.Then, for any ε > 0 and t ∈[0,Tmax), the corresponding solutions (u,v) of (1.2) satisfy which, by combining with (3.16)–(3.17), tells us that Lemma 3.3 holds.□ Then we consider the mass-critical p=2/N (N ≥2).In this case, the above method no longer applies, which requires us to consider the localized radial virial estimate (3.8).It is observed that if we choose a suitable radial function ϕ defined by (3.6) and ε > 0 as small as possible such that then, for R=R(ε)>0 sufficiently large, we have that and the radial solutions of (1.2) blow up in forward time before T∗2.Therefore, our tasks is now to find a suitable radial function ϕ to make (3.19) hold.Referring to [3, 12], let ϑ(r) be a real-valued function in W3,∞satisfying that It is easy to see that θ(r) satisfies (3.4).Letting radial function ϕ also be defined by (3.6), we claim that (3.19) is true for this choice of ϕ.Indeed, by the definition of ϕ and (3.20)–(3.21),it is not hard to check that Hence we can choose ε>0 as small as possible such that(3.19)holds true.For r >(1+1/3)R,it is easy to verify that ϑ′(r/R) ≤0, and thus χ1= 2-ϕ′′(r) ≥2 and χ2= (1+β)(2N -ϕ′′(r)-((N -1)ϕ′(r)/r)) ≤M for some constant M > 0.Then we can also choose ε > 0 sufficiently small such that (3.19) holds true.□ In this section we will give the proof of Theorem 1.2.First, we establish two types of invariant evolution flow under the hypotheses (1.7)–(1.8).t ∈[0,Tmax), the solutions (u,v) of (1.2) satisfy This, combined with (1.8), (4.4) and the continuity argument, allows us to claim that, for any t ∈[0,Tmax), (4.2) holds true.□ We are now in a position to prove Theorem 1.2. Proof of Theorem 1.2If (1.7) holds, we can choose δ > 0 as small as possible such that Choose R = R(δ,˜δ,M[u0,v0]) > 0 sufficiently large such that the right-hand side of (4.10) is bounded by a strictly negative constant.Thus, the maximum existence time Tmaxmust be finite.Similarly, when 0 Remark 4.2When p = 2/N (N ≥2), sc= 0.If E[u0,v0] ≥0 and ‖u0‖22+ ‖v0‖22sufficiently small, we claim that the solutions of (1.2) exist globally.This argument refers to the proof of the main theorem in Weinstein[16].Here,we give a brief proof for the convenience of the reader. Using (1.3)–(1.4), (2.1) and (2.5), we have that Conflict of InterestThe authors declare no conflict of interest.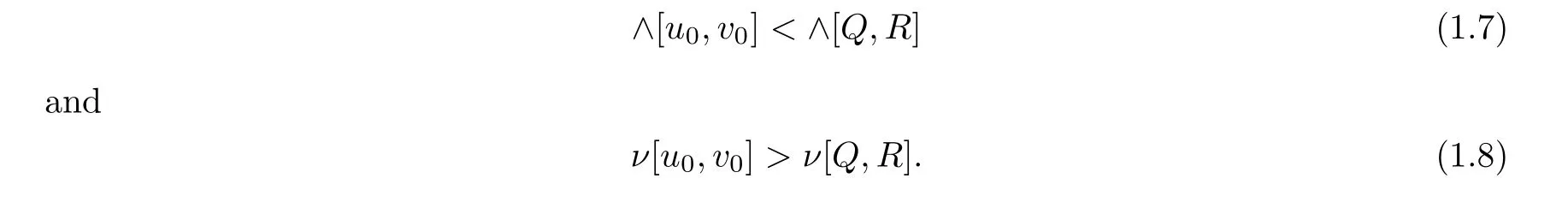
2 Preliminaries


3 Proof of Theorem 1.1




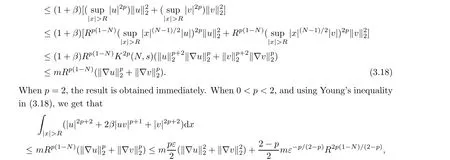

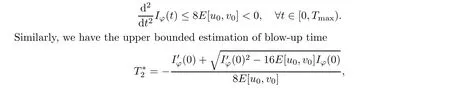
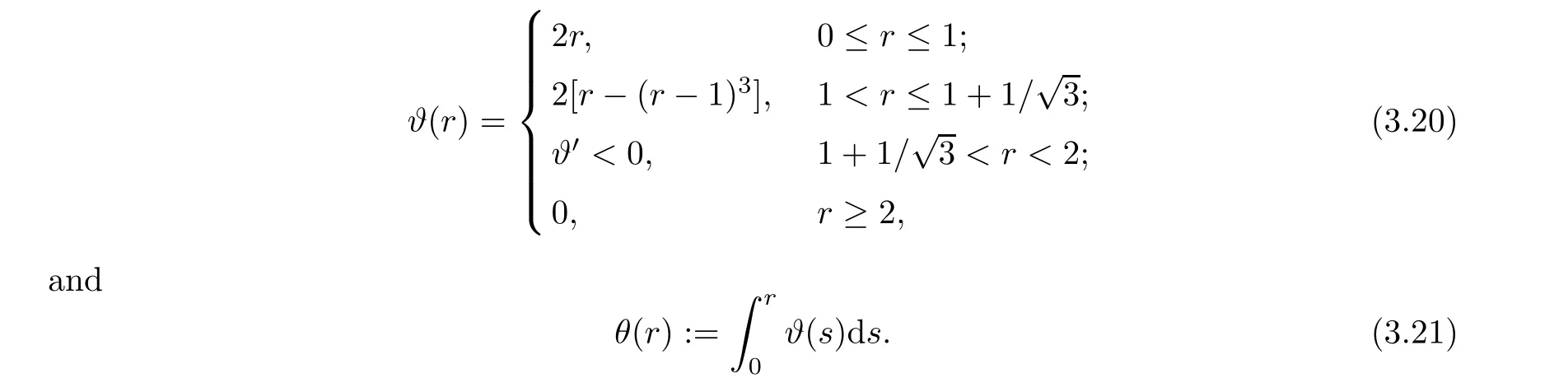
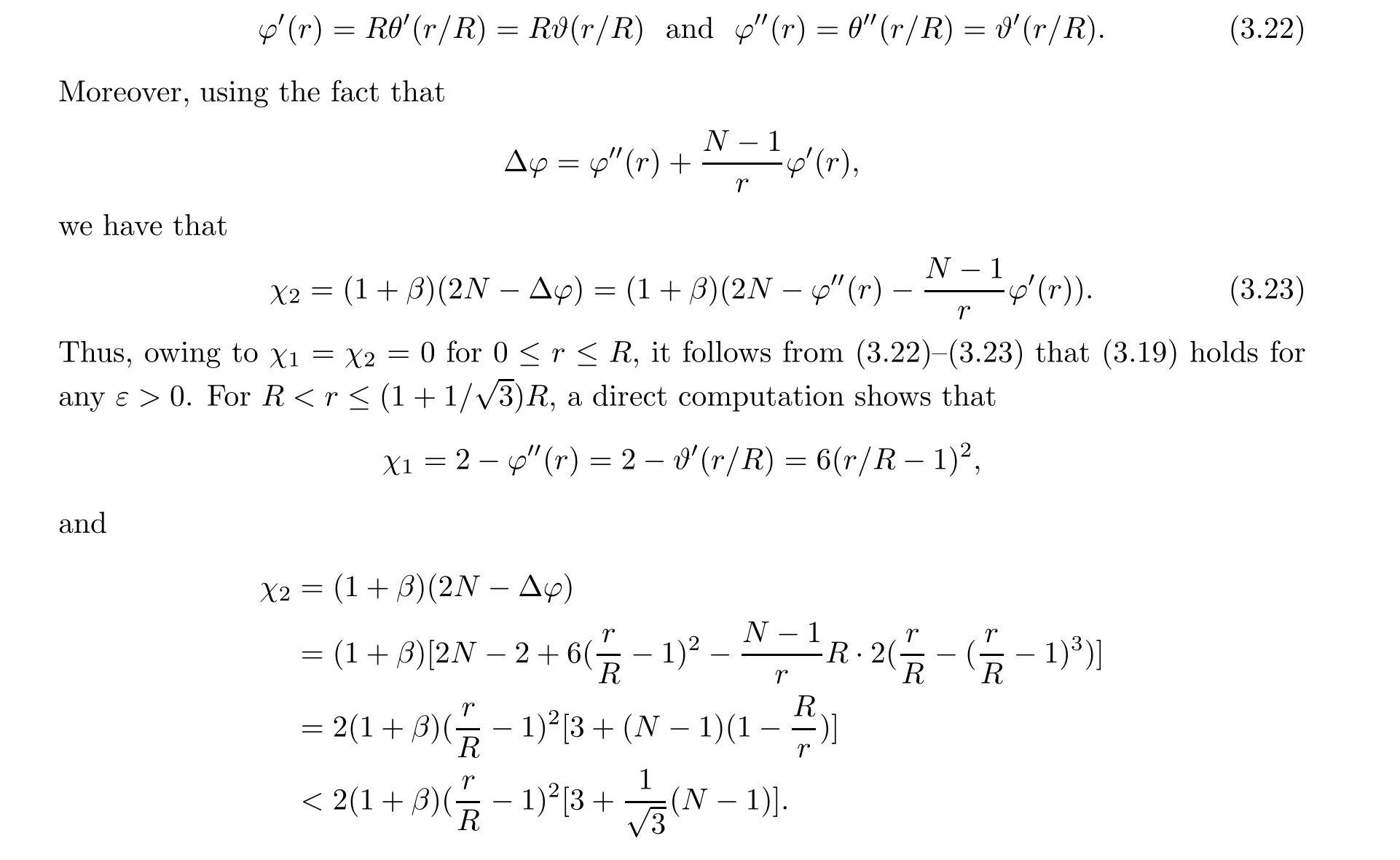
4 Proof of Theorem 1.2

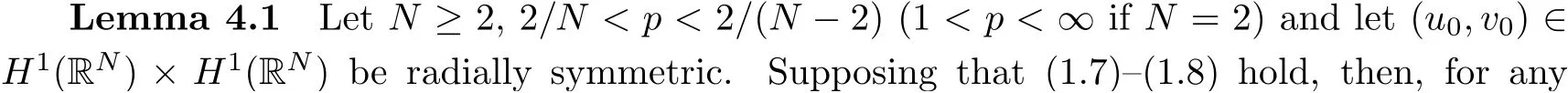


猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- NATURALLY REDUCTIVE (Q1, a2)METRICS*
- THE ENERGY CONSERVATION OF THELANDAU-LIFSHITZ-BLOCH EQUATION*
- MULTIPLE POSITIVE SOLUTIONS TO A CLASSOF MODIFIED NONLINEAR SCHRODINGER EQUATION IIN A HIGH DIMENSION*
- LARGE DEVIATIONS FOR TOP EIGENVALUES OF 3-J ACOBI ENSEMBLES AT SCALING TEMPERATURES*
- DISTORTION THEOREMS FOR CLASSES OFg-PARAMETRIC STARLIKE MAPPINGS OF REAL ORDER IN Cn*
- BOUNDEDNESS AND COMPACTNESS FOR THE COMMUTATOR OF THE w-TYPECALDERON-ZYGMUND OPERATOR ON LORENTZ SPACE*
