用矩阵形式的电路方程分析多层特斯拉线圈
2024-01-12陈希有李冠林
陈希有 金 鑫 李冠林 齐 琛
(大连理工大学 电气工程学院,大连 116024)
在许多高校的电路类课程中,都介绍了网络图论在电路理论中的应用。虽然内容的名称有所不同,例如文献[1]叫“电路方程的矩阵形式”,文献[2]叫“电路的计算机辅助分析基础”,文献[3]叫“电路图论和网络方程”,等等,但内容大都包括图的基本概念及图的矩阵表示;KCL、KVL及支路方程的矩阵形式;通过矩阵运算列写节点方程、回路方程与割集方程,等等。但是,由于教学基本要求和学时的限制,教学或教材中,得出矩阵形式的电路方程并简单举例后内容便终止,没有进一步介绍矩阵形式电路方程的应用,导致一些学生甚至青年教师们产生困惑:这种利用矩阵运算列写电路方程的过程,还不如凭观察列写来得简单。因此,影响了对这部分内容教与学的积极性。只有极少数学生,会在研究生阶段的网络分析与综合课程中,能够进一步理解矩阵形式电路方程的数学推演优势[4],大部分学生对学习这部分内容的目的性不甚明了。
本文在科研中制作了多层特斯拉线圈,用于研究谐振式电能传输。在建立线圈的电路模型以后,需要对其进行多种分析。该模型包含众多互感支路,经简化后,可以作为矩阵形式电路方程具体应用的很好案例,从而加深学生对学习电路方程矩阵形式目的性的理解,唤起求知欲望。
特斯拉线圈能够利用线圈的分布参数产生谐振。在特斯拉无线电能传输的论文中使用了此线圈[5]。因此,这样的案例也可让学生了解特斯拉及特斯拉线圈在电气与信息时代所发挥的基础作用,潜移默化中提高了对伟大发明家的敬仰之情。
1 多层特斯拉线圈及其电路模型
本文制作的多层特斯拉线圈如图1所示。线圈骨架为PVC管。低压绕组只有一层,位于最外层,采用利兹线且非紧密缠绕。高压绕组有7层,位于低压绕组层内。

(a) 实物图
由上述结构可知,多层特斯拉线圈各层之间均存在自感、互感,以及导线电阻;层与层之间存在电容。但高、低压绕组之间,由于绝缘纸较厚,且低压绕组匝数很少,因此高、低压绕组之间的电容相对较小,本文忽略不计。当不关心特斯拉线圈内部电磁行为时,可以用集中参数元件来近似表示上述分布参数,由此得到如图2所示的多层特斯拉线圈正弦稳态电路模型。
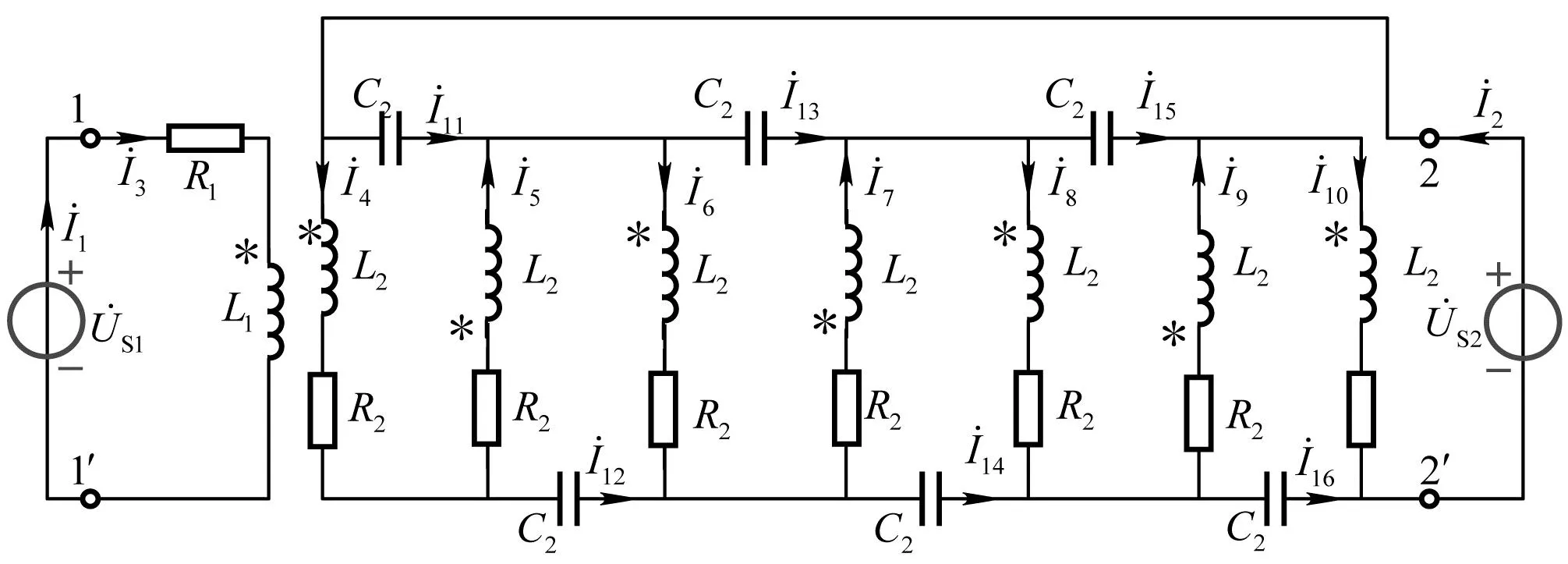
图2 多层特斯拉线圈正弦稳态电路模型
根据缠绕工艺进行合理简化,即均匀化。低压绕组每层等效电阻为R1、等效电感为L1;低压绕组与高压绕组每层之间的耦合系数均为k1、互感为M1。高压绕组每层等效电阻均为R2、等效电感均为L2,彼此之间的耦合系数均为k2、互感均为M2。上述参数的具体量值,可以通过计算或仿真来获得,本文将在仿真分析中直接给出结果。
特斯拉线圈用于电能变换与传输时,高压绕组要接负载或另一特斯拉线圈的高压绕组。但为了建立模型的等效电路,在分析时暂用电压源置换负载,如图2中的。
2 网孔电流方程的建立
由于模型中含有多个互感,宜使用以电流为变量的方法列写方程。为使方程个数尽可能少,宜采用网孔电流法。但是,当使用观察法列写网孔电流方程时,由于存在诸多互感,网孔之间的互阻抗很容易被漏掉或重复,或者发生符号错误。使用矩阵运算列写网孔电流方程,则可避免这些问题,这是因为分析者只需简单地写出网孔-支路关联矩阵、支路阻抗矩阵和支路电压源列向量,其余步骤都交给程序,按矩阵运算来建立方程。
画出图2的网络线图,如图3所示,它包含16条支路,8个网孔。因此网孔-支路关联矩阵有8行16列,如式(1)所示。

图3 电路模型(图2)的网络线图

(1)
让支路电压和支路电流具有关联的参考方向,它们的列向量分别记作

(2)


(3)
式中的Zb具有分块矩阵形式:

(4)
其中左上角对应电压源支路和电感支路的分块,是10行10列的对称矩阵,如式(5)所示。对角线元素对应支路阻抗;非对角线元素对应支路之间的互感阻抗。即
(5)
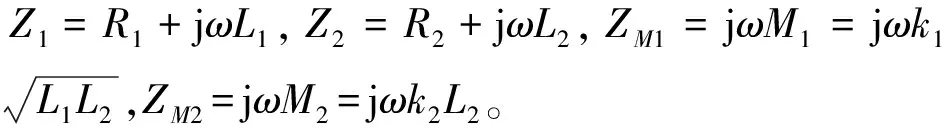
对应电容支路的右下角分块是对角矩阵:
ZC=diag[ZC2,ZC2,ZC2,ZC2,ZC2,ZC2]
(6)
式中,ZC2=1/jωC2。
图2中只有1、2支路含理想电压源,因此支路电压源列向量为,

(7)
再设待求的网孔电流列向量为,

(8)
根据KCL和KVL的网孔-支路关联矩阵形式,不难得到用矩阵运算表示的网孔电流方程[6]:

(9)
其中系数矩阵称为网孔阻抗矩阵,记作DZbDT=Zm,它的非对角线元素便是网孔之间的互阻抗。
网孔电流可通过网孔阻抗矩阵的逆并用下式来求得:
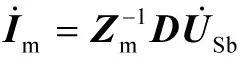
(10)
求出网孔电流后,还可以继续分析其他感兴趣的问题,以此彰显矩阵形式电路方程的数学推演优势,为矩阵形式的电路方程找到应用场景。选几个方面示范如下。
3 网孔电流对电路参数的灵敏度
灵敏度反映了电路特性对电路参数变化的敏感程度,用偏导数表示。灵敏度分析是电路分析与优化设计的重要内容[7-8]。使用矩阵形式的电路方程很容易计算各种灵敏度。
假设发生变化的参数是p(例如自感系数、耦合系数等),将网孔电流方程(9)对参数p求偏导数(矩阵对p的偏导数,等于该矩阵各元素对p的偏导数组成的矩阵,只需告诉学生这一规则即可):
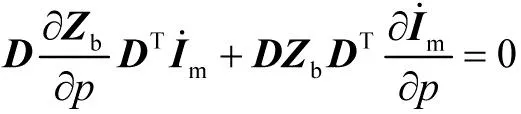
(11)
由上式求得网孔电流对参数p的灵敏度为,

(12)
4 二端口阻抗参数矩阵Z的计算


图4 特斯拉线圈的二端口网络模型
根据图2,网孔1、2的网孔电流同时也是图4的端口电流,因此二端口网络的阻抗参数方程可以表述成:
(13)
在方程(10)求解后,式(13)中电压和电流都是已知量,待求的是阻抗矩阵的4个元素。但两个方程不足以求出4个元素,为此,改变端口外接电压源,计算改变后的端口电流。由于是线性电路,所以端口电压与端口电流仍满足阻抗参数方程:
(14)
联立(13)和(14)便可求出阻抗参数矩阵元素。为便于使用计算机程序求解,以阻抗参数矩阵元素为待求量,将方程(13)和(14)合写成如下形式:

(15)
简记为

(16)
据此求得由阻抗参数矩阵元素组成的列向量:
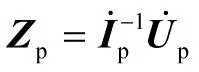
(17)
由Zp的计算结果得到图4的T形等效电路,如图5所示,图中各阻抗分别为

图5 特斯拉线圈的T形等效电路

(18)
5 阻抗参数矩阵对电路参数的灵敏度
由阻抗参数矩阵可以确定网络的许多特性,因此分析阻抗参数矩阵的灵敏度,是分析其他特性灵敏度的基础。
将式(16)两边对参数p求偏导数得
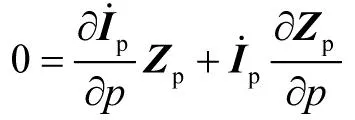
(19)
因此,由阻抗参数矩阵元素组成的列向量Zp对参数p的灵敏度可按下式计算:
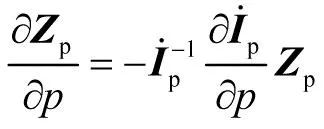
(20)
6 有载电压增益
在建立T形等效电路之后,将T形等效电路的端口2接入负载ZL,根据电路理论的米尔曼定理和分压公式,便可获得用等效电路参数表示的电压增益解析表达式,结果如下:

(21)
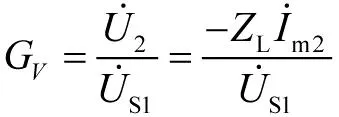
(22)
此时电压增益灵敏度可以通过网孔电流的灵敏度来得到:

(23)
7 仿真分析
7.1 网孔电流仿真


表1 网孔电流仿真结果
第1个网孔为低压绕组网孔,绕组匝数最少,因此电流最大。
7.2 网孔电流对耦合系数的灵敏度仿真
将耦合系数k1视为发生微小变化的参数p。式(12)中支路阻抗矩阵Zb对k1的偏导数写成分块矩阵形式就是:

(24)
根据式(5)列出的子矩阵ZL,它对k1的偏导数矩阵为10行10列对称矩阵:
(25)
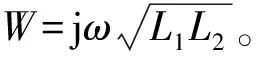
另一子矩阵因为不含k1,所以偏导数为零矩阵,即
(26)
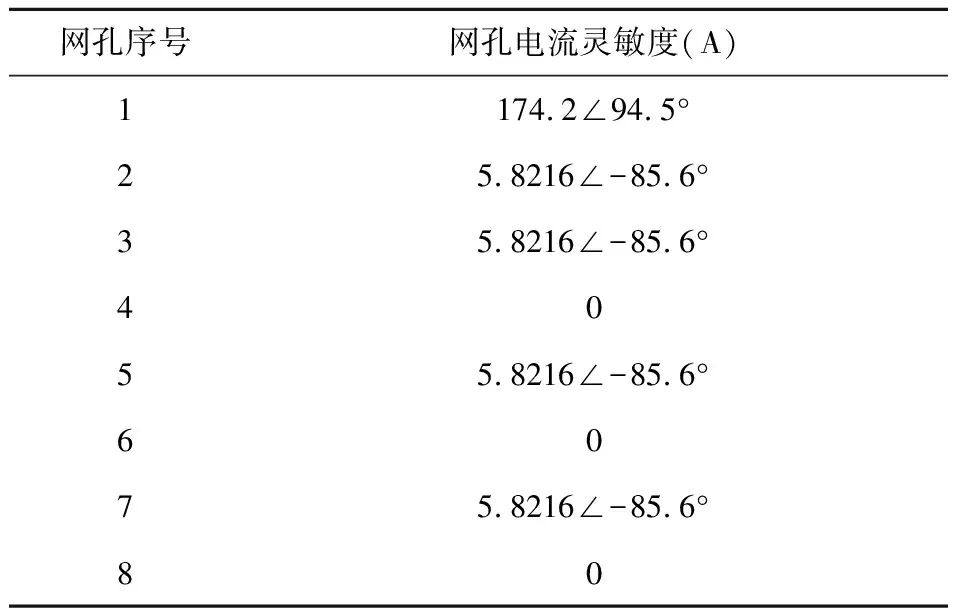
表2 网孔电流对耦合系数k1灵敏度
网孔4、6、8为层间等效电容电流,灵敏度为0,表明这些电流不受耦合系数k1的影响。
7.3 阻抗参数矩阵及灵敏度仿真
从表1可知,端口电流为
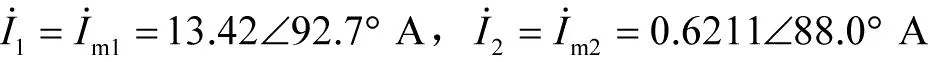


(27)
因此,图5所示的T形等效电路中各阻抗分别为
(28)
由式(20)计算阻抗参数矩阵对耦合系数k1的灵敏度,仿真结果如下:
(29)
可见∂Z22/∂k1=0,这是因为Z22是当端口1开路时,从端口2看进去的等效阻抗,显然与高、低压绕组之间的耦合系数k1无关。仿真结果与客观事实相符。
7.4 有载电压增益及灵敏度仿真
特斯拉线圈在谐振时有很大的电压增益,并且增益与负载阻抗有关。利用式(21)或(22)可以对增益的频率特性进行仿真。选择5种纯阻性负载,分别是20 kΩ、40 kΩ、60 kΩ、80 kΩ和100 kΩ,得到增益的幅频特性,如图6所示。随着负载电阻的增加,电压增益变得越来越陡峭,但峰值对应的频率基本不变,约为24.2 kHz。
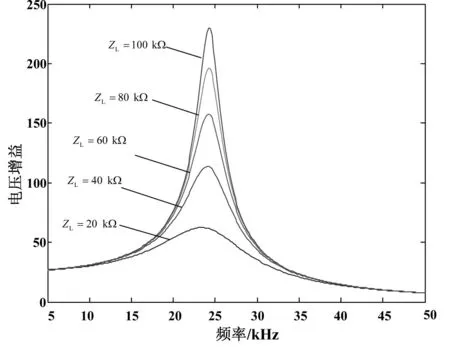
图6 有载电压增益的幅频特性
8 结语
将矩阵形式的电路方程应用到特斯拉线圈分析中,可以促进学生对矩阵形式电路方程实用性的认识,并激发教师在科研中努力提炼教学案例,为抽象的电路理论内容找到具体的应用对象,做到学有所用。
