新疆射月沟水库溃坝过程数值模拟
2024-01-12钟启明李大成梅胜尧
马 黎,钟启明,杨 蒙,吴 迪,李大成,梅胜尧
(1.中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081; 2.南京水利科学研究院,江苏 南京210029; 3.水利部水库大坝安全重点实验室,江苏 南京 210029)
近年来,受全球气候变化影响,我国极端暴雨事件呈增加趋势[1]。2000 年1 月至2021 年12 月,我国共发生99 起溃坝事故,多起溃坝事故发生在干旱和半干旱地区,其中新疆和内蒙古自治区分别发生9 起和6 起由极端暴雨导致的溃坝事故[2-3]。如2018 年7 月31 日,位于新疆自治区哈密市的射月沟水库大坝因坝顶溢流发生溃决[4]。合理预测溃坝过程对溃坝洪水致灾后果的评价具有重要意义,采用数值分析方法模拟溃口流量过程和溃口尺寸演化过程是预测溃坝过程的有效手段。目前常用的溃坝过程数学模型可分为经验模型和基于溃决机理的模型[5-7]。经验模型一般通过考虑坝体形态、水库特征、坝料特性等信息,基于回归分析或机器学习方法建立经验计算式,获取溃坝时的溃口峰值流量、最终溃口尺寸和溃坝历时等溃坝参数[5]。但经验模型无法获取溃坝时的溃口流量过程和溃口发展过程。基于土石坝溃决机理的溃坝过程数学模型[8-14],一般采用宽顶堰流或孔流公式模拟漫顶或渗透破坏溃坝时的溃口流量,并利用各种冲蚀公式来描述坝料的输移,一些模型还可以考虑溃口边坡的失稳[13-14],通过按时间步长迭代的数值计算方法获取各时间步长的溃口流量和溃口尺寸。
本文通过对射月沟水库溃坝案例的调研,总结溃坝水流的冲蚀特性和溃口发展过程。在此基础上建立基于坝体溃决机理的简化漫顶溃坝过程数学模型,反演射月沟水库的溃坝过程,并与国外典型的NWS BREACH 模型的计算结果进行对比分析。
1 射月沟水库溃坝事件调研
射月沟流域地处哈尔里克山南坡,由6 条支流汇流形成射月沟水库(图1)[15]。射月沟水库集水面积约408 km2,径流补给主要由季节性冰雪融水、夏季降雨和泉水组成,年平均降雨强度约为150 mm,年平均径流量为1.58×107m3。

图1 射月沟流域水文概况Fig.1 Hydrological survey of Sheyuegou Basin
射月沟水库大坝距离二宫村头宫队2 km,距离哈密市115 km。大坝为沥青混凝土心墙砂砾石坝,3 层沥青混凝土心墙厚度均为0.4 m,坝顶高程为1 496.65 m,防浪墙顶高程为1 497.65 m;大坝最大坝高41.15 m,坝顶长403 m、宽6 m,上、下游坡比(垂直/水平)分别为1∶2.25 和1∶2.00[16],射月沟水库大坝典型断面见图2。
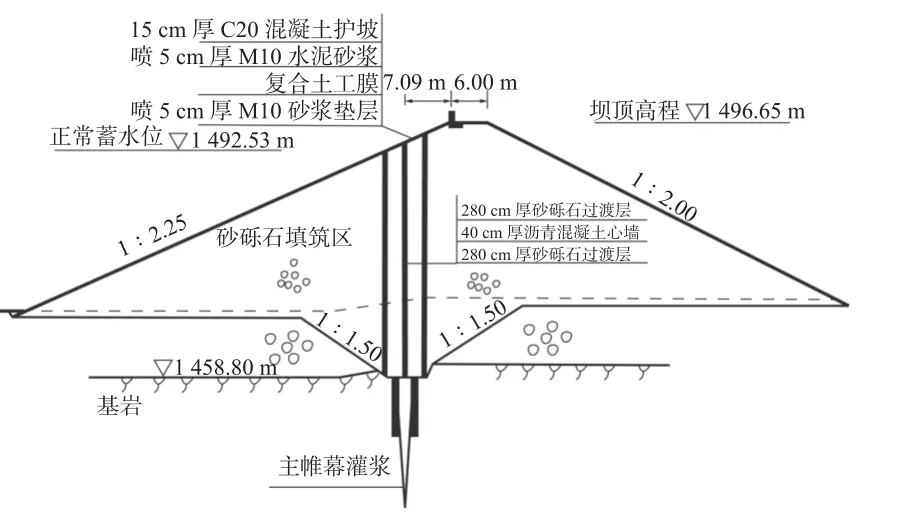
图2 射月沟水库大坝典型断面示意Fig.2 Schematic diagram of the typical section of Sheyuegou reservoir dam
1.1 2018 年“7·31”洪水产汇流过程
2018 年7 月31 日01:00 至13:00,射月沟流域发生特大暴雨,小堡、射月沟、秦城3 个气象站12 h的降水强度分别为116、105 和79 mm(3 个气象站位置见图1),均打破了当地的极值记录[17]。2018 年7 月31 日22:00,新疆自治区水文局基于坡面面积法,通过现场洪水痕迹调查,得出射月沟水库入库洪峰流量达到1 848 m3/s,远超设计标准,导致水库发生漫顶溃坝。赵悬涛等[15]通过模拟获取了射月沟水库2018 年7 月31 日的降雨-入库流量过程(图3),入库峰值流量相对误差仅为3.6%,在本文的溃坝过程模拟中采用此入库洪水流量过程线。
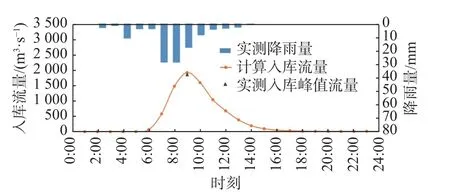
图3 射月沟水库2018 年7 月31 日降雨-入库流量过程线Fig.3 The rainfall-inflow hydrograph of Sheyuegou reservoir on July 31, 2018
1.2 射月沟水库漫顶溃坝过程
2018 年7 月31 日8:00 至11:40,一名目击者用手机录制了射月沟水库溃坝过程的多段视频。虽然视频是临时拍摄的,但获取的信息对研究人员直观了解坝体冲蚀特性和溃口形态演变过程具有重要意义。
根据现场视频,可将射月沟水库溃坝过程分为4 个阶段:(1)初始冲坑出现。水流越过坝顶后表现为全断面溢流,由于坝顶处水流流速较小,顶部未出现明显冲蚀;受重力作用,水流在下游坡行进时流速逐渐增大,导致下游坡某一位置的土体发生冲蚀,形成初期冲坑(图4(a))。(2)溯源冲蚀。在漫顶水流的作用下,冲坑以上下游坡逐渐变陡,直至接近垂直;随后发生溯源冲蚀,在此过程中下游坡面几乎保持垂直,冲蚀不断向上游发展(图4(b)~(c))。(3)初始溃口出现。当溯源冲蚀发展至上游水库后,由于坝顶高程突然下降,初始溃口出现,漫顶水流汇聚到溃口处,其他部位的漫顶冲蚀结束(图4(d))。(4)溃口扩展。随着漫溢水头的逐渐增大,溃口在横断面和纵断面的冲蚀逐渐加快;由于溃口形态的快速变化,溃口边坡发生失稳;当溃口处水流的剪应力小于坝料的临界启动剪应力时,冲蚀过程停止(图4(e)~(f))。

图4 射月沟水库溃坝过程照片Fig.4 Photos of the Sheyuegou dam breach process
根据溃坝视频和现场调查,大坝内部的沥青混凝土心墙无法抑制溃口的发展,其原因主要有两个方面:一是沥青混凝土心墙均位于坝体上游部位(图2),主要起防渗作用,对初期溃口的发展影响微弱;二是溯源冲蚀发展至沥青混凝土心墙位置时,溃口处的漫溢水头已达到较大值,仅有40 cm 厚度的沥青混凝土心墙无法阻止溃口的发展。因此在数值模拟中不考虑心墙。
2 基于溃决机理的简化漫顶溃坝过程数学模型
基于射月沟水库漫顶溃坝过程的视频和现场调查资料,建立基于物理机制的简化溃坝数学模型。由于坝体溃决时间相对较短,渗流的影响可以忽略不计。模型主要包括4 个部分:溃口流量计算、初始冲坑位置确定、纵断面溃口发展和横断面溃口发展。
2.1 溃口流量计算
水量平衡是溃坝模拟中必须遵循的基本原理,利用水量平衡关系描述水库水位变化关系:
式中:As为与库水位相对应的库面面积;zs为库水位;t为时间;Qin为入库流量;Qb为溃口流量;Qs为溢洪道泄流量;QT为闸门泄流量。
溃口流量可采用宽顶堰流量方程[18]表示:
式中:c1和c2分别为流量系数,其中c1= 1.7 m0.5/s,c2= 1.3 m0.5/s[18];b为溃口底宽;H=zs-zb,其中zb为溃口底高程;m为溃口边坡坡比(垂直/水平)的倒数;ksm为尾水修正系数[18-19]。
2.2 初始冲坑位置确定
根据相关文献[20-21],土石坝溃坝时初始冲坑的位置计算如下:
式中:ln为从下游坡顶顺坡至初始冲坑的距离;β0为大坝下游坡角;dn为下游坡法向水深;Frn为初始冲坑处的弗劳德数;Un为水流在初始冲坑处及越过冲坑后的法向平均流速,Un=C(Rnsinβ0)1/2=C(Hsinβ0)1/2,其中C为谢才系数,Rn为水力半径;g为重力加速度;Bw为坝顶处漫顶水流的顶部宽度;Bn为下游坝坡处漫顶水流的顶部宽度;当漫顶水流越过初始冲坑后,dn=Qb/(UnBn)。由于溃坝第一阶段为全断面溢流,因此假设Bw=Bn。
2.3 纵断面溃口发展
根据射月沟溃坝案例的视频记录,在数学模型中可将溯源冲蚀过程分为两个阶段:(1)初始冲坑出现后,水流继续掏刷冲坑,下游坝坡坡角逐渐变大至基本垂直,形成陡坎;(2)陡坎保持直立状向上游发生运移,直至进入水库。
溃口的底床冲蚀率采用基于剪应力的冲蚀公式[22]表示:
式中:E为底床冲蚀率;kd为坝料冲蚀系数,可通过试验测量[23]或经验公式计算[24],即kd= 10(ρw/ρd)exp,其中ρw为水的密度取1 000 kg/m3,ρd为坝料的干密度,cr为坝料的黏粒含量;τb为溃坝水流的剪应力,可通过曼宁公式计算[10];τc为坝料颗粒的临界起动剪应力,可由希尔兹曲线[25]获取。
对于下游坝坡变陡阶段,坡角增量计算如下:
式中:dβ/dt为下游坡角变化率;E1为冲坑处的底床冲蚀率;E0为坝顶处的底床冲蚀率。
对于陡坎运移阶段,利用时间平均的冲蚀率公式来计算溯源冲蚀率[26]:
式中:dx/dt为陡坎运移速率;CT为陡坎运移系数;q为溃口单宽流量;He为陡坎高度。
随着陡坎的运移,陡坎上游侧的坝体在纵断面方向逐渐变薄,在水动力作用下可能沿水平面破坏,可通过比较坝体在水平破坏面上的驱动力和抵抗力来评价陡坎上游侧坝体的稳定性。驱动力由上游水压力和陡坎底部的水流剪应力组成,而抵抗力则包括水平破坏面和陡坎两侧的黏聚力和摩擦力及尾水引起的水压力。当驱动力大于抵抗力时,陡坎上游侧坝体会发生失稳破坏,并假定失稳的坝体物质在瞬间被漫顶水流冲走,至此溯源冲蚀发展至水库。
2.4 横断面溃口发展
当溯源冲蚀发展至水库后,漫顶水头突然增大,坝体横断面出现初始溃口,根据射月沟溃坝视频假设初始溃口的形状为矩形。随着水流的不断侵蚀,初始溃口迅速加深加宽,当溃口深度达到临界高度时,溃口边坡沿平面发生失稳破坏,初始溃口由矩形变为倒梯形,此后漫顶水流继续冲蚀溃口直至溃坝结束。
假设漫顶水流对溃口底部和侧壁具有同等的冲蚀能力,则溃口顶宽增量为:
式中:ΔBt为溃口顶宽增量;nloc为溃口位置参数(nloc= 1 代表单侧冲蚀,nloc= 2 代表双侧冲蚀);α为溃口边坡坡角。
溃口底宽增量表示为:
式中:ΔBb为溃口底宽增量。
利用极限平衡法评价溃口边坡的稳定性,当失稳块体自重引起的驱动力大于失稳块体自重和土体黏聚力引起的抵抗力时,溃口边坡发生失稳破坏。视频记录和其他模型试验表明,边坡失稳时的破坏面近乎平面,并假定失稳土体被溃坝水流瞬间冲走。溃口边坡失稳的驱动力Fd和抵抗力Fr分别为:
式中:W为失稳块体重力;θ为失稳后的溃口边坡坡角;γs为边坡土体重度;Hs为溃口边坡的临界高度;φ为土体内摩擦角;C为土体黏聚力。
采用按时间步长迭代的数值计算方法模拟溃坝过程中的水土耦合效应,每个时间步长可输出溃口流量、溃口尺寸、库水位等溃坝参数。
3 射月沟水库溃坝案例数值模拟
采用上述建立的数学模型对射月沟水库溃坝过程进行反演分析,通过视频记录和现场实测数据,验证模型的合理性,并对关键输入参数进行敏感性分析。
3.1 输入参数
从拍摄的视频中可以看到,射月沟水库大坝于7 月31 日9:10 开始漫顶溢流,并在当日11:00 左右溃坝结束。模拟持续时间为3 h,时间步长为1 s。根据视频记录,将溃坝计算时的初始水位设置为1 497.75 m,超过防浪墙顶高程0.1 m,入库流量过程如图3 所示。坝料冲蚀系数(kd)和陡坎运移系数(CT)是溃坝模拟的重要指标。根据设计报告,ρd=2 240 kg/m3,cr= 0.04,由前文经验公式可得,kd=3.0 cm3/N/s。另外,基于溃坝过程视频确定的陡坎移动时间,推导出CT= 0.001 /m1/6/s2/3。表1 给出了射月沟水库和坝体的物理力学指标[4,16]。

表1 模型输入参数Tab.1 Input parameters of the numerical model
3.2 计算结果分析
由于初始漫顶溢流的水位为0.1 m,由式(4)可以得出,初始冲坑位于下游顶部顺坡向下8.93 m 处。计算结果显示,陡坎在溃坝后0.90 h(对应时间为10:04)进入水库,现场观测时间为10:00,计算结果与实测数据吻合较好。另外,根据计算结果,在溃坝后1.38 h(对应时间为10:33)出现溃口峰值流量,这也与实测数据10:25 出现峰值流量相吻合。
表2 给出了射月沟水库溃坝案例的计算和实测溃坝参数,包括溃口峰值流量(Qp)、溃口最终顶宽(Btf)、溃口最终底宽(Bbf)、溃口最终深度(Df)和溃口峰值流量出现时刻(Tp)。从表2 可以看出,溃口峰值流量、溃口最终顶宽和底宽、溃口峰值流量出现时刻的计算误差均较小。由于没有溃口流量过程和溃口形态发展过程的实测数据,仅有推求的峰值流量和实测最终溃口尺寸,图5 和图6 主要展示了溃口流量过程和溃口形态发展过程的计算值。另外,从图5 和图6 的变化趋势看出,坝体横断面和纵断面溃口形态的演变趋势与现场视频记录相吻合,这表明本文所提出的数值模拟方法能够较为准确地描述射月沟水库的溃坝过程。

表2 射月沟水库计算与实测溃坝参数值对比Tab.2 Comparison of numerical and measured breaching parameters of Sheyuegou reservior
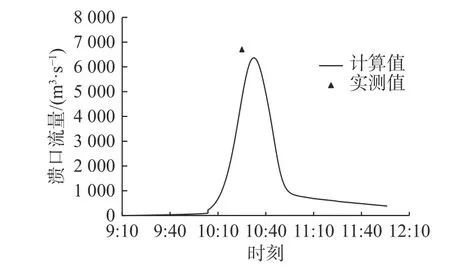
图5 溃口流量过程计算值与溃口峰值流量实测值Fig.5 Numerical and measured results of breach flow discharge

图6 溃口形态发展过程计算值与溃口最终尺寸实测值Fig.6 Numerical and calculated results of breach development
3.3 参数敏感性分析
在射月沟水库溃坝过程的数值模拟中,坝料冲蚀系数(kd)和陡坎运移系数(CT)是具有高度不确定性的关键输入参数。kd对溃坝过程中的冲蚀率有较大影响,是决定溃坝过程和溃口尺寸的关键参数;CT直接决定陡坎的运移速率,也对溃坝过程具有重要影响。通过将数学模型中的相关参数(kd和CT)分别乘以0.5 和2.0,重新计算射月沟水库的溃坝过程,分析模型分别对这2 个参数的敏感性。表3 和表4 分别显示了在不同kd和CT条件下,模型计算出的溃口峰值流量、溃口最终尺寸(长度、宽度和深度)和溃口峰值流量出现时刻的变化情况。图7 和图8 还分别比较了不同kd和CT条件下的溃口流量过程。

表3 不同坝料冲蚀系数(kd)对溃坝过程的影响Tab.3 Influence of different dam material erodibility coefficients (kd) on dam breach process

表4 不同陡坎运移系数(CT)对溃坝过程的影响Tab.4 Influence of different headcut migration coefficients (CT) on dam breach process
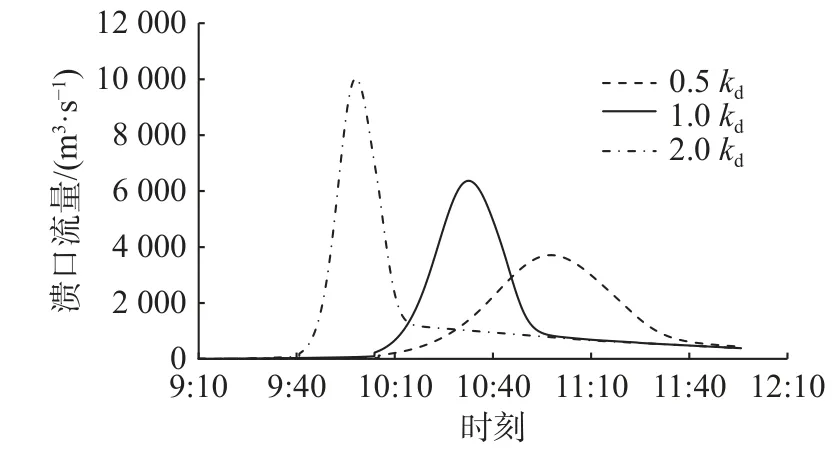
图7 不同坝料冲蚀系数kd 条件下的溃口流量过程Fig.7 Breach hydrographs under different kd
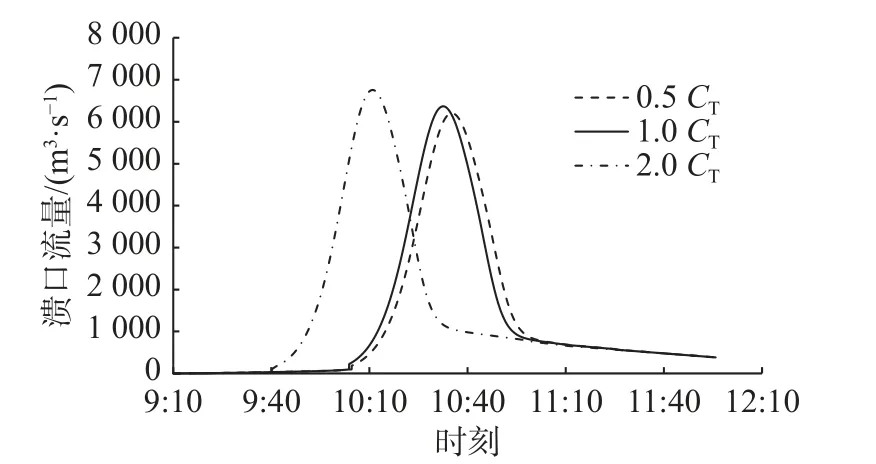
图8 不同陡坎运移系数CT 条件下的溃口流量过程Fig.8 Breach hydrographs under different CT
对于冲蚀系数(kd),各溃坝参数的总体敏感性由强到弱依次为:溃口峰值流量,溃口峰值流量出现时刻,溃口最终尺寸。当冲蚀系数增大1 倍或缩小至50%时,溃口峰值流量将分别产生57.5%和−41.7%的变化,而溃口峰值流量对溃坝致灾后果评价具有重要意义,因此在选取参数时应注重其合理性。对于陡坎运移系数(CT),由于原始模型中CT的取值较小,当CT缩小至50%时,对计算结果的影响较小;当CT增大1 倍时,各溃坝参数的敏感性有所增强,尤其是溃口峰值流量出现时间,较原始模型提前了23 min。各溃坝参数的总体敏感性由强到弱依次为:溃口峰值流量出现时刻、溃口最终尺寸、溃口峰值流量。总体而言,kd主要影响溃口峰值流量和溃口峰值流量出现时刻,而CT主要影响溃口峰值流量出现时刻。
4 与典型溃坝模型比较
选择美国NWS BREACH 模型[8]模拟射月沟水库的溃坝过程,然后通过计算结果比较其与本文模型的优缺点。选择NWS BREACH 模型的原因在于,该模型也是基于溃决机理的简化漫顶溃坝过程数学模型,且目前在国际上应用较广泛。表5 列举了NWS BREACH 模型和本文模型的特点。

表5 NWS BREACH 模型和本文模型的特点总结Tab.5 Summary of characteristics of NWS BREACH model and the present model
NWS BREACH 模型采用修正Meyer-Peter-Mueller 公式[27]模拟坝料的冲蚀过程,其中起控制作用的参数是d90/d30(d90和d30分别为小于该粒径的颗粒质量占总质量30%和90%对应的颗粒粒径),反映了坝料颗粒的分布特征。根据射月沟坝料的颗分曲线[4],d90/d30约为45。模型其他输入参数可参考表1。
表6 对比了NWS BREACH 模型和本文模型预测的溃坝参数结果及相对误差。图9 为2 个模型预测的射月沟水库溃坝过程中的溃口流量过程线。

表6 不同基于溃决机理的简化溃坝模型计算结果对比Tab.6 Comparison of numerical results of different simplified physically-based dam breach models

图9 不同基于溃决机理的简化溃坝模型预测的溃口流量过程Fig.9 Predicted breach hydrographs of different simplified physically-based dam breach models
由表6 和图9 可以看出,NWS BREACH 模型预测的溃坝参数和溃口流量过程与本文模型相比表现出更大的相对误差。由于坝料的冲蚀特性对溃坝过程至关重要,而NWS BREACH 模型中决定冲蚀系数的关键参数是d90/d30,射月沟水库的堆石材料表现出宽级配的特征,且d90/d30= 45,导致坝料的冲蚀率较大,因而预测得到的溃口峰值流量偏大,峰值流量出现时刻提前,溃坝历时缩短。虽然NWS BREACH模型预测的溃口流量过程线呈现出较大的误差,但由于溃坝历时较短,溃口形态后期无明显扩展,因此溃口最终形态误差较小。通过射月沟水库溃坝实例的比较发现,本文模型的预测精度总体高于NWS BREACH 模型。
5 结 语
根据射月沟水库溃坝过程的视频记录和现场调查,本文建立了基于溃决机理的描述水库溃坝过程的简化数学模型。利用射月沟水库溃坝案例的实测资料对模型的准确性进行验证,并通过与其他典型溃坝模型预测结果的对比,证明了本文模型预测结果的合理性。主要结论如下:
(1)射月沟水库的溃坝机制主要表现为纵断面方向初始冲坑的形成与溯源冲蚀,以及横断面方向溃口的连续下切、侧向冲蚀和溃口边坡的间歇性失稳坍塌。此外,随着冲蚀的不断加剧,纵断面方向大坝下游坡角逐渐减小,而横断面溃口的边坡角基本保持不变,直至发生溃口边坡失稳。
(2)参数敏感性分析表明,坝料冲蚀系数对溃坝过程有显著影响,溃口峰值流量和溃口峰值流量出现时刻对坝料冲蚀系数的敏感性大于溃口最终尺寸,且溃口峰值流量对坝料冲蚀系数的敏感性最高。另外,溃口峰值流量出现时刻比其他溃坝参数对陡坎移动系数更为敏感。因此,在进行溃坝模拟时,坝料冲蚀系数和陡坎移动系数的选取至关重要。
(3)因坝料冲蚀率公式的选择和对纵、横断面溃口发展过程计算方法的过度简化,目前广泛应用的NWS BREACH 未能合理描述射月沟溃坝过程的特点。但由于对土石坝溃决过程的认识不足,且测量数据存在较大的不确定性,因此仅通过单个溃坝案例难以全面展示各模型的功能。本文对模型预测能力的对比仅作为参考,未来仍需对各模型的精度开展进一步验证。
