单根箔条平均雷达截面研究

2024-01-12吕思潼高梦竹金福禄陈振龙

舰船电子对抗 2023年6期

吕思潼,高梦竹,金福禄,陈振龙

(1.空军航空大学,吉林长春 130022;2.解放军93069部队,辽宁大连 116200)

0 引言

箔条的使用由来已久,它是应用最广泛的一种无源干扰器材。箔条具有显著的干扰效果,并且可以对抗多种雷达体制。箔条主要通过箔条的电磁散射特性来完成对雷达接收机的干扰。箔条受到电磁波照射后,在入射交变电磁场作用下,产生一定的感应电动势,并感应交变电流,依据电磁场辐射理论,交变电流要向外辐射,这就是散射。箔条的雷达截面就是表征箔条散射能力强弱的参数。目前在单根箔条平均雷达截面的研究上,讨论非常广泛,形成的理论结果也比较多[1-6]。对单根箔条电磁散射特性的研究最早可追溯到半个世纪以前,主要是对金属细导线、金属圆柱体的研究。1947年Van Vleck等人在文章[7]中引用了朱兰成未发表的公式作比较,利用谐振金属丝球状模型得到了每根细金属丝平均雷达截面数值。文献[8]～[10]对非相干条件下箔条偶极子的散射雷达截面进行了研究。但由于各种方案在建立坐标系、采用的方法、假设不同,以及考虑到了不同的影响因素,所得的结果存在一定的差异。文献[11]指出直接把各偶极子平均雷达截面的算术和作为整个云团的雷达截面是粗糙的,它没有考虑到箔条云中每一个散射场之间的相位关系,即各子散射场在接收天线处的相干合成。尤其当箔条云在空间中的位置分布趋于稳定时,这种相干因素的影响就更为显著。本文旨在围绕箔条建立统一的空间取向坐标系,不断完善影响箔条雷达截面的因素并进行严格推导,得到更贴近于实际使用的理论数值。

1 非相干条件下单根箔条平均雷达截面

由前苏联学者瓦金C A提出的理论结果0.17λ2成为具有代表性的半波长箔条平均雷达截面值。但该理论体系存在局限性,模型建立不完备。它只是考虑到了电磁波极化与偶极子的夹角关系,忽略了电磁波在空间中的传播方向。

1.1 固定入射波极化条件下单根箔条平均雷达截面

考虑到传播方向因素的影响,围绕箔条建立空间直角坐标系,如图1所示。

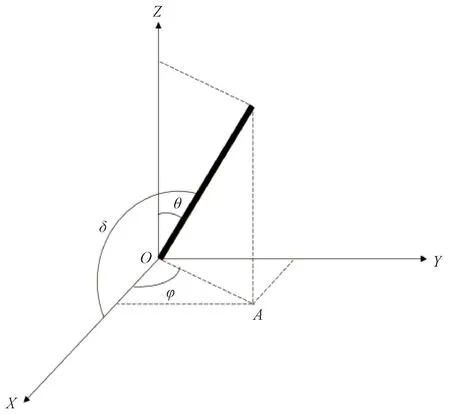
图1 半波长箔条空间取向三维直角坐标系

图1中,入射波为线极化波,X轴为电磁波极化方向,Z轴负方向为雷达照射波入射方向,在箔条处的场强大小为E。OA为箔条在XOY面内的投影,θ为箔条与入射方向的夹角,φ为OA与X轴之间的夹角,δ为箔条与入射波极化方向的夹角。

入射电场在箔条上激励起感应电流。根据入射波与箔条之间的位置关系,可以得到箔条上腹值电流大小为:

(1)

式中:R∑为辐射电阻。

由此箔条在空间中散射的电场可以表示为:

(2)

根据图2几何关系,cosδ=sinθcosφ。

图2 箔条空间取向直角坐标系改进

将上述两式联立得:

(3)

σs≈0.853λ2cos2δf2(θ)

(4)

散射场Es可分解为x极化、y极化2个分量,这2个分量模值可分别表示为:

Esx=|Es|cosφ

(5)

Esy=|Es|sinφ

(6)

从而得到雷达截面σxx、σxy:

σxx=0.853λ2cos2δf2(θ)cos2φ

(7)

σxy=0.853λ2cos2δf2(θ)sin2φ

(8)

式中:σxx表示当入射波为x极化,接收天线为x极化时对应的雷达截面,即同极化通道;σxy表示当入射波为x极化,接收天线为y极化时对应的雷达截面,即交叉极化通道。

考虑到箔条在三维空间的任意分布,则在该情况下单根箔条对应的平均雷达截面为:

(9)

(10)

同理,当入射波电场为y极化时,单根箔条对应的平均雷达截面为:

(11)

(12)

1.2 任意入射波极化条件下单根箔条平均雷达截面

在实际作战中,入射波极化方向随机,对于任意极化方向的入射波,需要借助极化散射矩阵对箔条的散射特性进行研究。在图1坐标系的基础上,定义入射波极化为任意方向,对坐标系进行修正如图2所示。

图2中,Z轴负方向为电磁波入射方向,θ表示电磁波传播方向与箔条轴线的夹角,φ表示电磁波极化方向与X轴的夹角,φ代表箔条在XOY面内投影与X轴的夹角,δ表示电磁波极化方向与箔条轴线之间的夹角。定义Ex、Ey为入射波极化在XOY面内的分量,有:

Ex=|E|cosφ

(13)

Ey=|E|sinφ

(14)

结合式(1),得到:

(15)

由半波长箔条二次散射产生的辐射场场强可以表示为:

(16)

由式(15)和式(16)联立得,半波长箔条对应的极化散射矩阵为:

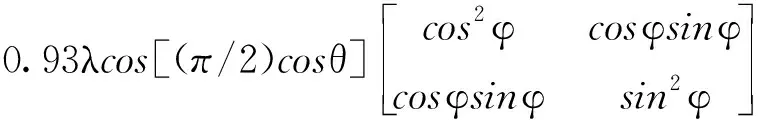
(17)

由雷达截面(RCS)定义式得,RCS与极化散射矩阵中对应元素呈平方关系,半波长箔条RCS可以表示为:

(18)

如图3所示,图3(a)代表同极化条件下箔条散射截面的变化,图3(b)代表交叉极化条件下箔条散射截面的变化。由图3(a)分析,当θ=π/2,φ=π时,箔条RCS为最大值,达到0.86λ2。可以解释为当入射电磁波电场方向与箔条极化方向(箔条轴线方向)平行时,箔条散射能力最强;反之,当入射电磁波电场方向与箔条极化方向(箔条轴线方向)垂直时,箔条没有散射能力。由图3(b)可知,交叉极化RCS并不为0,是由于散射时具有主瓣宽度,在对抗单脉冲角跟踪时采用的交叉极化干扰就是基于交叉极化通道的散射特性。同时由图3(a)和图3(b)的对比得,同极化RCS峰值约为交叉极化RCS峰值4倍。

图3 同极化/交叉极化通道散射截面

考虑到半波长箔条在空间中的球面均匀分布,得到半波长箔条极化散射统计特性:

(19)

式中:σ11、σ22代表同极化通道散射特性;σ12、σ21代表交叉极化通道散射特性。

2 群体效应下单根箔条平均雷达截面

箔条云是由大量箔条组成的,考虑到相干散射模型,箔条云的散射总能量是每根箔条在雷达接收机天线处的相干合成。在计算箔条云团整体的雷达截面时,采用通常的迭代法、解析法对不同时刻每一根箔条的雷达截面进行求解,最后再进行叠加,计算量大且难以实现。因此,在计算时可以将箔条云团划分为一定的箔条云层,计算每个箔条云层的雷达截面,再考虑到箔条云层之间的遮挡效应将不同箔条云层进行叠加。文献[12]中提到分层结构在效率和精度上满足对雷达信号反射研究的要求。箔条云层的雷达截面受箔条数量及箔条排列方式的影响。现提出一种箔条云层的理想摆放模型,如图4所示。

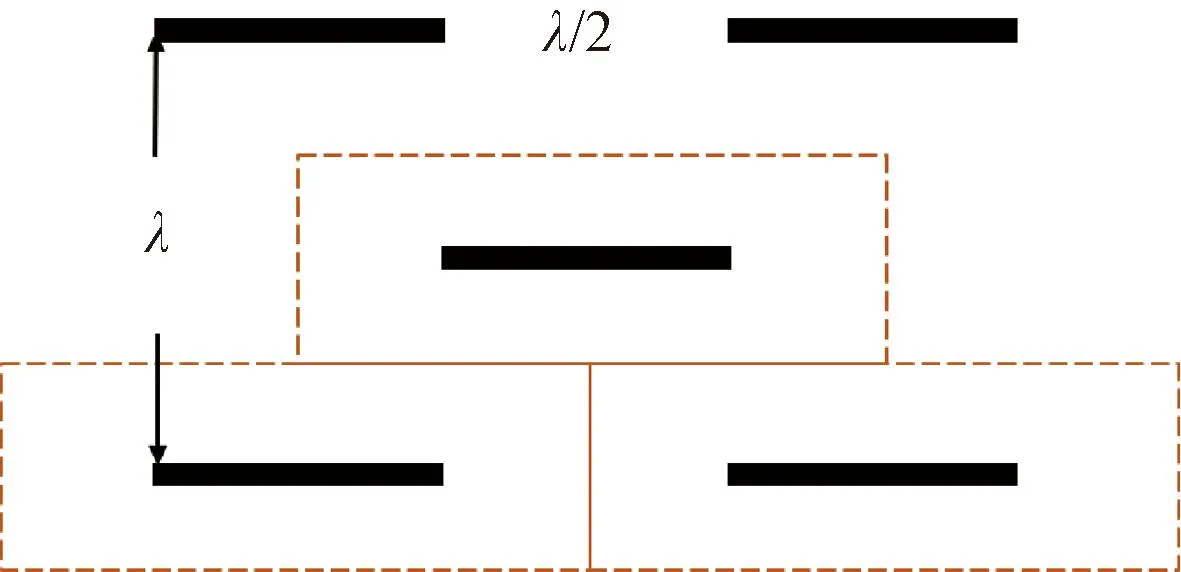
图4 箔条云理想摆放位置

雷达截面可作如下定义:目标的雷达截面是指这样一种(虚构的)面积,该面积截获的雷达辐射功率在全方向上均匀散射时在雷达处产生的回波功率等于目标在雷达处产生的回波功率。由定义可知,处于光学区目标的RCS为:

σ=AG

(20)

式中:A为目标面积;G为增益。

如果箔条处于最佳摆放位置,半波长箔条的位置关系及间隔如图5所示,箔条与箔条之间在垂直和水平方向上均间隔λ/2,单根箔条所占面积为λ2/2。半波对称振子的方向性系数值为1.64,增益与方向性系数之间的关系为G=Dη。如果效率按100%来近似的话,半波振子的增益值也为1.64。通过以上分析,可以得出单根箔条在最佳摆放位置时的雷达截面为:

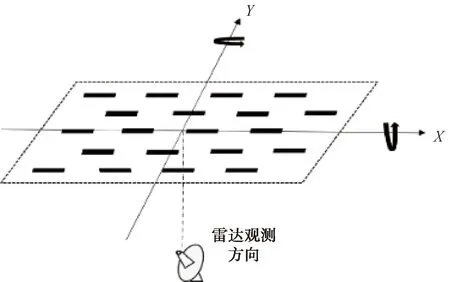
图5 理想摆放位置时箔条云的空间分布

(21)

此时,雷达来波方向为箔条云层法线方向,照射电磁波的极化与箔条云中单根箔条轴线方向平行。

接下来讨论雷达来波入射角度的变化对该理想分布情况下单根箔条RCS的影响。将箔条云层看作一个整体,对于观测方即雷达所在位置而言,箔条弹打出后经过一定的散开时间,箔条云在空中的分布趋于稳定,实际上影响箔条云RCS大小的主要因素为观测位置的不同。不同的观测角度对应不同的有效面积,从而产生RCS的差异。为了便于分析,将观测位置相对固定,转向考虑箔条云层的不同空间分布态势。

构建坐标系如图5所示,其中X、Y轴组成水平面。假定入射波方向为箔条云层法线方向,当箔条云层按以下2种方式变化时,会带来有效面积的改变。

方式一:箔条云层绕X轴旋转一定的角度θ,考虑到箔条云层在空间中球面均匀分布,记θ∈[-π,π];

方式二:箔条云层绕Y轴旋转一定的角度φ,考虑到箔条云层在空间中球面均匀分布,记φ∈[-π/2,π/2]。

当箔条云层绕X轴旋转一定的角度θ后,对于观测方向上的有效面积产生了衰减,衰减因子为cosθ。由于单站条件下雷达对目标的观测是通过电磁波双向传播完成的,实际上有效面积的衰减对RCS的影响是双重的,即有效面积的变化对电磁波的收发均产生相同的影响。综上,箔条云层绕X轴旋转θ角度后,对RCS的衰减系数为cos2θ。同理,箔条云层绕Y轴旋转φ角度后,对RCS的衰减系数为sin2φ。

最后还需要考虑电磁波极化对RCS的影响。可以看到,当箔条云层绕X轴旋转时,电磁波极化与单根箔条轴线方向保持平行的态势,不产生影响;当箔条云层绕Y轴旋转时,电磁波极化与单根箔条轴线方向产生φ的夹角,由此对RCS产生系数为sin2φ的衰减。

通过以上分析,得出单根箔条在理想摆放位置时的平均雷达截面为:

(22)

该数值与朱兰成所得到的理论数值相符合,并且采用了更加直观的方式。但在实际使用过程中,很难存在理想摆放情况,再考虑到箔条云层之间的遮挡及环境衰减,单根箔条的平均雷达截面数值还会有所下降。