船舶冰区航行阻力预估法中人工神经网络的应用
2024-01-11李成海辛小辰刘树锋俞启军胡甚平





摘 要: 为保障极地冰区航行船舶的安全,冰阻力精准预估作用重大.近年来,人工神经网络(artifical neural network,ANN)机器学习在船舶领域得到了广泛应用.利用机器学习法设计一个预估极地船舶航行冰阻力模型,参照已有的经验公式,选取高质量特征参数进行输入,经过充分船舶模型实验数据演练此模型神经网络,以建立径向基(radial basis function,RBF)神经网络模型为基础,运用遗传计算法(genetic algorithm,GA)对模型优化处理.研究结果表明,以输入的7个高质量特征参数进行的遗传计算法,对径向基的神经网络(RBF-GA)模型进行优化的效果具有较强的泛化作用,与实船实验数据比对模型实验数据,证明其平均误差不大于8%,其精度较高的特点,可应用于冰阻力预估实操工作.
关键词: 极地地区;船舶航行;冰阻力;遗传计算法;径向基神经网络;船舶模型实验
中图分类号:U661.31+1"" 文献标志码:A"""" 文章编号:1673-4807(2024)06-044-08
收稿日期: 2023-12-12"" 修回日期: 2021-04-29
基金项目: 国家重点研发计划项目(2021YFC2801000,2019YFB1600602)
作者简介: 李成海(1965-),男,教授,正高级船长,研究方向为海上航行安全.E-mail: LICHENGHAI@163.com
引文格式: 李成海,辛小辰,刘树锋,等.船舶冰区航行阻力预估法中人工神经网络的应用[J].江苏科技大学学报(自然科学版),2024,38(6):44-51.DOI:10.20061/j.issn.1673-4807.2024.06.007.
Application of artificial neural network in the prediction methodof ship navigation resistance in ice areas
LI Chenghai1 , XIN Xiaochen1,LIU Shufeng1,YU Qijun2, HU Shenping3
(1.Department of Navigation, Shandong Transport Vocational College, Weifang 261206,China)
(2.The First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266100,China)
(3.School of Merchant Shipping, Shanghai Maritime University, Shanghai 201306, China)
Abstract:In order to ensure the safety of ships sailing in polar ice regions, accurate prediction of ice resistance plays an important role. In recent years, artificial neural network (ANN) machine learning has been widely used in the field of ships. In this study, the machine learning method is used to design a model to predict the ice resistance of polar ships. With reference to the existing empirical formula, high-quality characteristic parameters are selected for input, and the model neural network is drilled by sufficient ship model experimental data. Based on the establishment of radial basis function (RBF) neural network model, genetic algorithm (GA) is used to optimize the model. The research results show that the genetic algorithm based on the input seven high-quality characteristic parameters has a strong generalization effect on the optimization of the radial basis neural network (RBF-GA) model. Compared with the real ship experimental data, it is proved that the average error is less than 8%, and its high accuracy can be applied to the prediction of ice resistance.
Key words:polar region, ship navigation, ice resistance, genetic algorithm, radial basis function neural network, ship model experiment
随着北极航线的开放,极地冰区船舶航行成为热点问题.其中,有效保障船舶航行安全,精确预估冰阻力成为评估极地地区船舶航行能力最重要因素.因为海冰建构模型极其复杂及船舶破冰为一非线性动态过程,所以目前为止还没有一个高精确度的冰阻力预估方法.
目前,根据冰况、船舶形状及船舶与冰相互作用等因素,采用数值分析法、全尺度实验法、冰池模型实验法和经验及半经验计算式法计算冰阻力,其中,全尺度实验法和冰池模型实验法可靠性较强,但其成本高昂且耗时过长.文献[1]通过平整冰非线性的显式有限元法,模拟、实验取得科考船无量纲化的冰阻力系数值计算结果和对比,证明此方法计算可靠性.文献[2]运用离散元理论,构建离散元的计算数值模型方法对冰厚及船艏倾角影响进行预估.文献[3]利用光滑粒子的流体水动力学计算法构建船、冰和水耦合的数值模型,对不同的工况下船舶冰阻力预估分析.文献[4]利用理论解析法模型和数字高程模型(digital elevation model,DEM)相结合方法,对冰的挤压破坏和弯曲破坏及劈裂破坏进行模拟,揭示了船舶冰阻力具有的特性.以上研究大多运用经验公式以总阻力的分量预估平整冰的冰阻力,有关碎冰阻力的研究成果极少;因而,需新的高精度模型实现冰阻力的预估.
近年来人工神经网络(artificial neural network,ANN)机器学习应用在船舶领域,比较回归模型法及其他统计法,其具有可靠性高和泛化能力强的优点,可较好处理非线性复杂问题.文中参照经验公式法选取适合输入的特征量,利用船舶模型实验数据作为人工神经网络模型演练的数据,分析皮尔逊关联性及预处理演练数据,建立径向基函数(radial basis function,RBF)神经网络模型并利用遗传计算法(genetic algorithm,CA)优化网络.将模型实验和实船实验作验证分析对象,并比对分析径向基神经网络模型和径向基的神经网络(RBF-GA)模型预估结果.
1 冰阻力预估法
1.1 人工神经网络模型
自动建模的学习法可用于函数分类近似及回归等非线性的复杂问题,人工神经网络型是分析学习机器领域最常见的学习方法,以技术手段对人的大脑神经功能特征和网络结构进行模拟,其实质是一个非线性并行的大规律动态体系.单一的神经单元功能有限且结构相对简单,但多种经单元构成的网络体系有强大的泛化功能.人工神经网络型是一组计算机法所组成,此计算法经过输入的数据集演练,找到最优设定目标问题的函数,成为计算非线性高维度方面切实可行的好方法,输入船长、冰厚度等特征量数量越多,输出结果可靠程度越大,其演练模型稳定性越高,但在选取偏差和方差等特征量时需构建平衡关系,为预估提供优异泛化效果.
人工神经网络型法研究取得了一定效果,在船舶航行领域也开始了应用.文献[5]根据船舶艉部试验的数据,提出利用艉部进行先行模式的冰阻力计算法;文献[6]通过构建碎冰海冰离散元式模型,取得航速、冰厚、冰直径、海冰密度不同条件下冰阻力变化的规律.
目前,针对人工神经网络法冰阻力预估分析研究较少,已有研究效果中,一定范围的冰阻力预估的准确度相对准确,但取得一个预估精度更高的模型,需要研究方面更多.构建可靠性高的冰区船舶航行冰阻力预估模型,不仅具有优异的泛化能力,更需要高效计算和优异映射(非线性)能力.径向基神经网络为一三层前向的神经网络,此网络收敛效果好,能高速逼近非线性的任意函数.所以径向基神经网络在函数逼近领域具有广泛应用,如非线性的控制和识别模型等方面.
1.2 冰阻力预估的经验法
为方便构建一高可靠性冰阻力预估模型,选取适当神经网络的输入参数非常必要.为选择适合输入特征的神经网络,分析了经验式运用参数.依据6种半经验式,探索主要冰阻力的影响参数:
(1) Kim教授根据风级及冰航行模型与实船试验,M-9及M-5盐水冰及淡水冰模型试验冰阻力的有效值.依据此数值,总结了冰阻力预估公式,设定为冰密度、冰厚度、冰弯曲度和船舶航速的函数.
(2) Vance教授依据全尺度USCG Katmai Bay试验,提出来一和船舶长度与密度关联的最优回归方程式,可预估航行状态破冰船遭遇的阻力.
(3) Phillips和Zahn教授全尺度实验USCG Mobile Bay,提供出冰阻力计算公式.冰阻力、冰厚度和船舶资料主尺度的函数.
(4) 依据波的尼亚湾实船实验,Lindqvist教授提出冰阻力预估计算公式,将阻力划分为浸没、弯曲和破碎3部分,计算公式代表了冰弯曲度、冰的摩擦系数、冰厚度、船体的形状系数和船舶的主要尺度参数等的函数.
(5) 更新Lindqvist和Lonov教授的方程式,Riska教授提出平整冰况阻力预估公式及方程式,此方程式来自于波罗的海进行的多船全尺度实验取得的一组全系统经验系数,此系数表明了船舶速度和冰阻力间存在线性关系.
(6) Keinonen教授分析了5艘破冰船的研究,同时开展冰阻力预估研究并提出了自己的计算方程式.这些方程式和海上环境温度、冰弯曲度、船舶类型及船舶尺度有关.
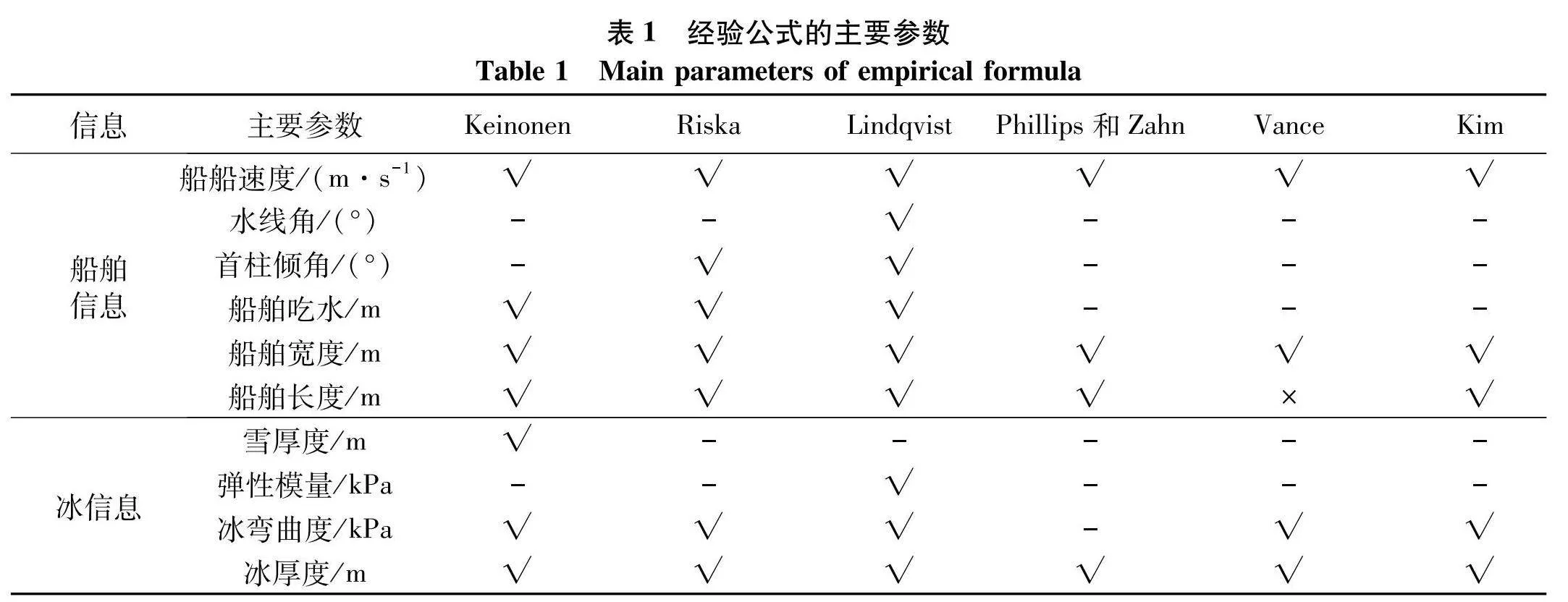
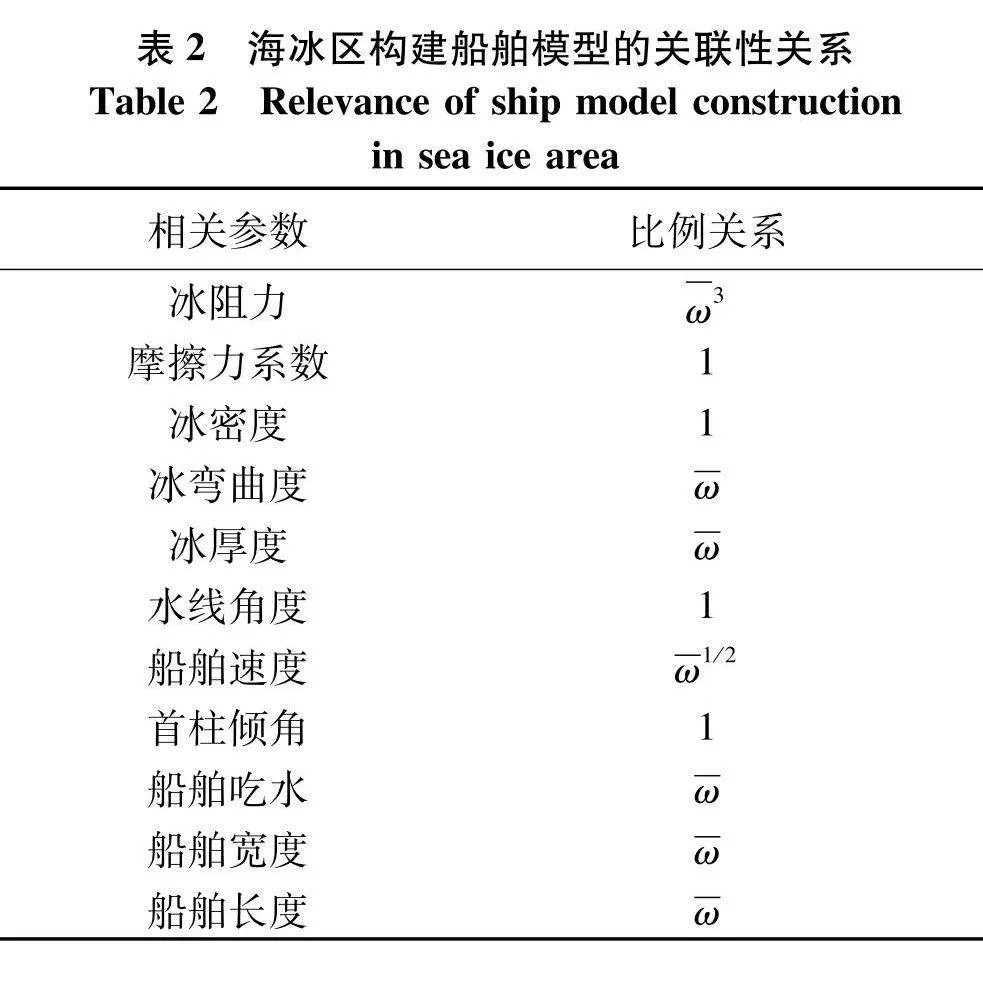
6位教授及教授团队提出的公式最大程度的表明了冰阻力主要的影响因素,见表1.
从表1可知,弯曲度、冰厚度、船舶速度、船舶宽度和船舶长度被各经验公式采用,而雪厚度和弹性模量及水线角均很少.考虑到ANN在输入特征的物理特点具有强大的抗干扰力,分析了实船实验及模型试验中参数的出现频次,特别是输入特性其物理特征对ANN没有影响;为此,研究选取冰弯曲度、冰厚度、船舶速度、首柱倾角、船舶吃水、船舶宽度及船舶长度作为7个特点性的参数输入量,输出值则为冰阻力.分析冰阻力和特点输入间进行的相关皮尔逊系数,且进行了归一化数据集处理,如表2.
2 数据集及特点的神经网络演练
2.1 构建数据集
建立ANN模型过程中,收集数据集资料非常关键.为保证模型预估精度,全面和详实数据收集是基础.因为全尺度的实验数据资料相对不足,研究取自18种不同模型实验获取的140组数据组成数据集,此数据集有验证集和演练集组成,以2∶8作为分割比例.表3为船舶和数据集相关参考文献研究效果[7-10].所有模型实验取得的数据转换成全尺度关联关系,演练集数据依据设置比例因子ω进行全尺度放大.
从表3可知,极区船舶航行主要遭遇的冰为平整形冰,适合模型实验取得结果.
在理想状态下,全尺度的船舶实验是确认船舶航行冰阻力最精确、最高效的方法.但因其实验耗时长且经费昂贵及无重复性的原因,所以,通常情况下可利用船舶模型实验来代替.因为尺度效应,对模型实验数据变换成全尺度数据会产生一定程度的误差.Schwarz教授比对了全尺度实验冰阻力与CCGS FRANKLIN 破冰船模型实验,比对结果证明,8%误差范围内,模型实验可进行船舶的初步设计程序,所以,文中选取船舶模型实验数值做ANN数据集合.
2.2 预处理数据
为提升神经网络模型预估精准度和收敛速度,亟需缩放特征值,以保持维数在可比较范围,文中利用归一化的方法缩放特征值,以便演练后取得每一特征值权重在同一个尺度内[8].归一化式为:
z′=z-zminzmax-zmin(1)
式中:z′、z为归一后和归一前的数据;zmin、zmax为特征量最小值和最大值.
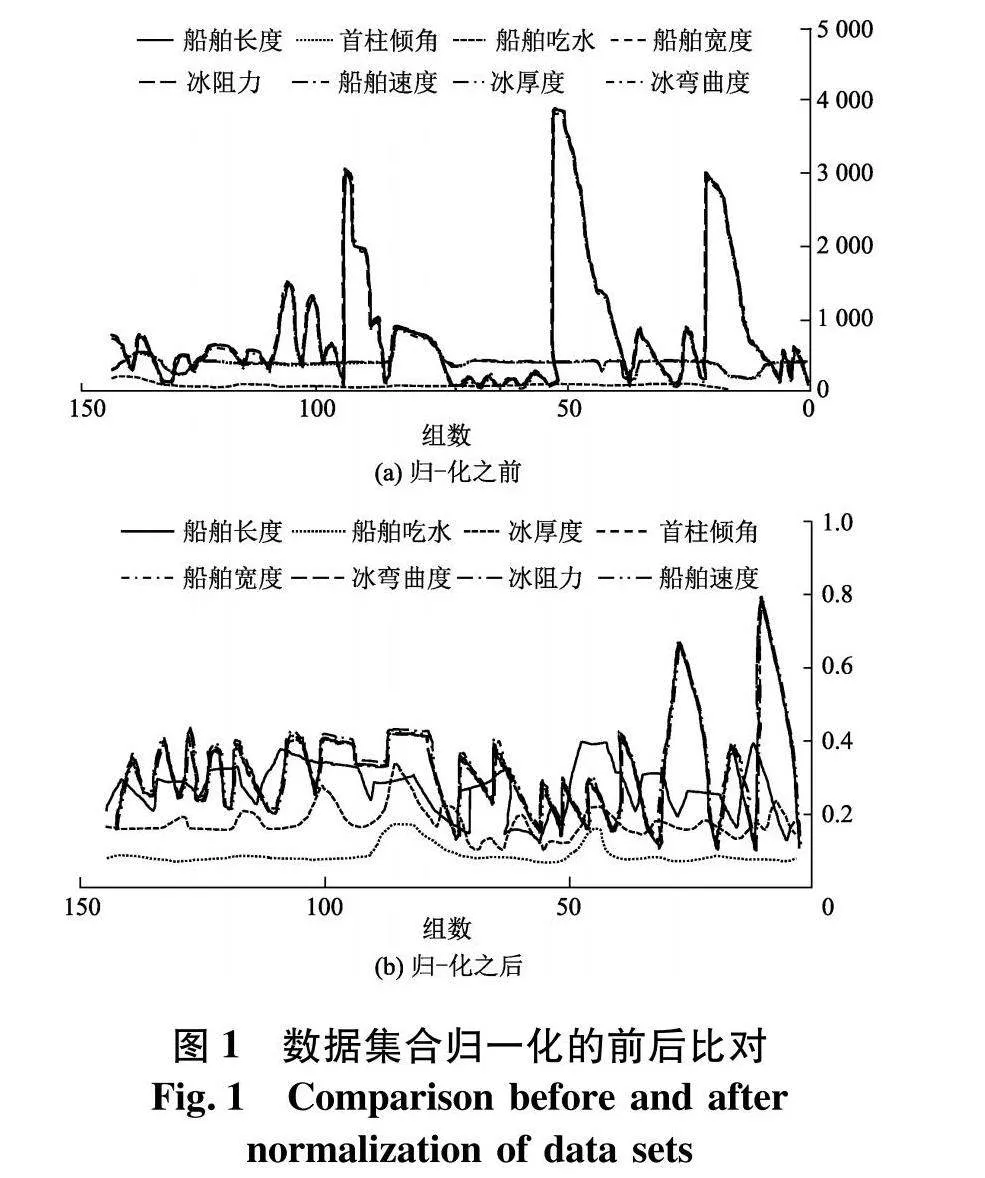
缩放后特征量值范围[0,1],从图1可知,归一化前输出和输入的特征值均不在可比较范围,各个特征量间互不影响;但归一化后各特征量间相互作用相互影响.
为方便量化输出与输入的特征量间存在的线性关系,将皮尔逊理论引入两者关系系数:
ρx,y=cov(x,y)ψxψy=G{(x-δx)(y-δy)}ψxψy=
Gxy-G(x)G(y) Gx2-G2(x) Gy2-G2(y)(2)
式中:ρx,y为皮尔逊关联系数;cov(x,y)为变量x与y之间协方差;ψx与ψy为变量x与y标准的偏差;G为数学期望,这其中x、y均经归一化处理.
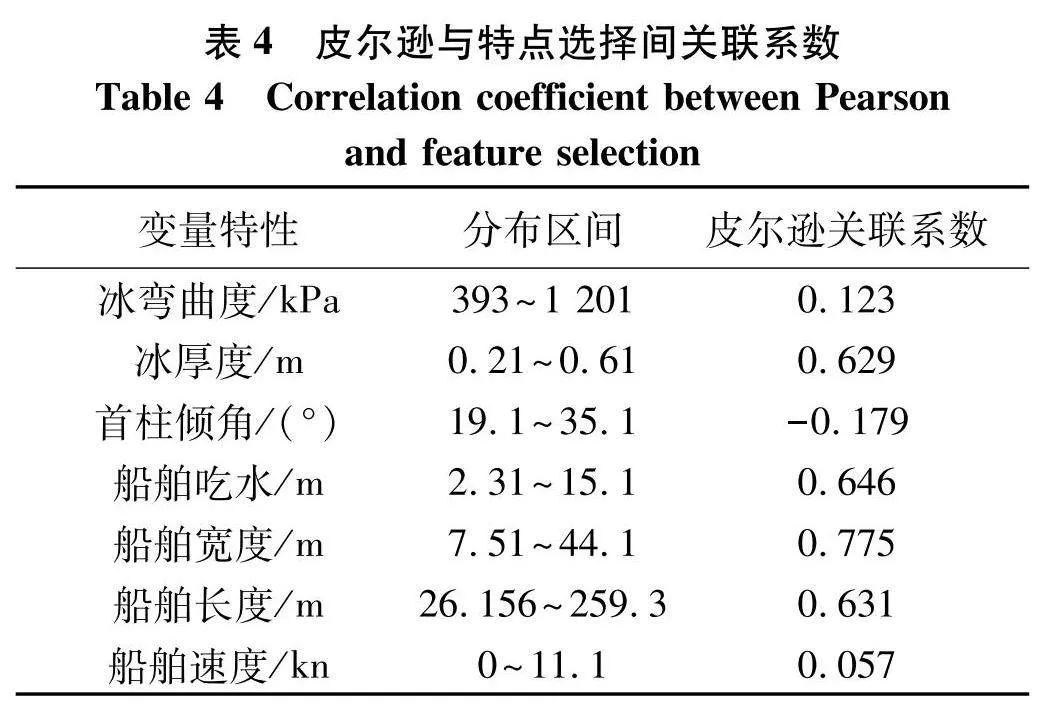
表4列出冰阻力与7个输入特点性之间线性的关联性.从表4可知,船舶长度、船舶宽度、船舶吃水及冰厚度和冰阻力间高度相关联,然而冰弯曲度和首柱倾角对冰阻力期望值及依存度较小,冰阻力与船舶速度间近乎相关性.
在进行航行船舶模型实验时,参数与数据的选取记录受到实验环境影响,其部分因素可能被忽略或者理想化.其一例证为,Lindqvist公式未分析破碎冰强度对于冰阻力产生的影响,相对于破碎冰强度较小的波罗的海海域冰况存在合理性,但对于航行于其他海域的船舶进行的全尺度实验中,当冰存在强大破碎强度时,总体冰阻力极有可能被低估.因为皮尔逊关联系数选取于数据库[9].表4表明,冰阻力与船舶速度间存在的皮尔逊关联系数较小,表示船舶速度对冰阻力产生的影响较小,皮尔逊关联系数仅存在量值线性关系,当关联性参数为0时,同样存在关联关系.
3 模拟神经网络演练
3.1 前向性神经网络
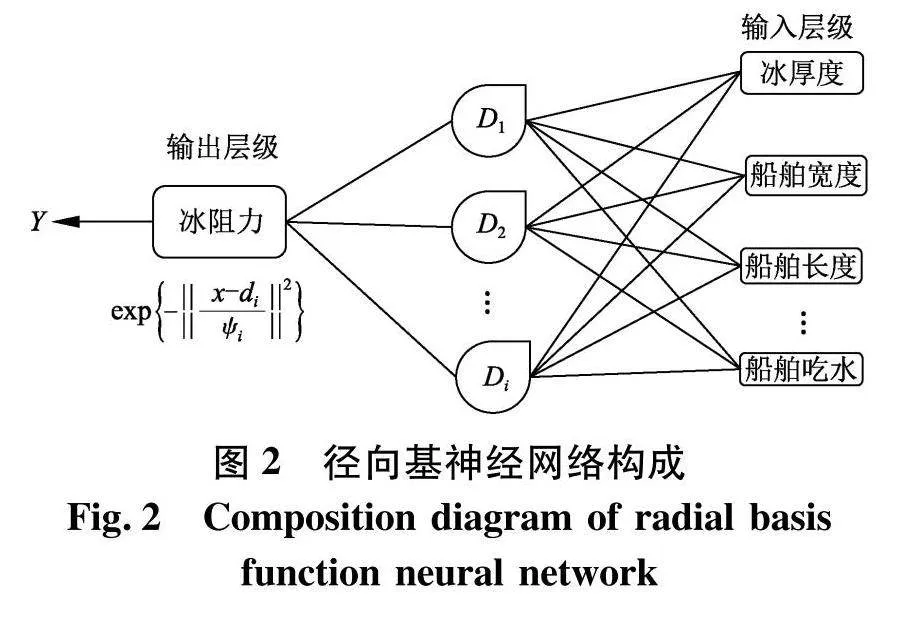
RBF为前向性神经网络,神经单元与输入参数构成了网络输出前向性神经网络函数线性集合,其构成,见图2.
前向性神经网路激活函数为:
Vxf-dj=exp[-12ψ2‖xf-dj‖2] (3)
式中:‖-dj‖为欧式范数;dj为高斯函数中心;ψ为高斯函数方差.
输出阶层函数为:
yi=∑rj=1qjiVxf-dj i=1,2,…,m(4)
式中:xf为第f个输入样本;dj为网络隐含阶层结点中心;qji为隐含阶层到输出阶层连接的权值;r为隐含阶层的结点数;yi为输入样本相对应网络输出的节点实际输出值.
RBF-GA模型与RBF函数关系可各自表示为:
y1=Q1×exp[-12ψ21‖X-a1‖](5)
ψ1=1.404,Q1=-0.024 6-0.024 9-0.024 7-0.024 9-0.024 6-0.024 8-0.024 9-0.025 4-0.024 5-0.024 9 , a1=0.417 40.049 80.902 80.944 90.491 00.489 40.337 80.900 20.369 30.111 3
式中:Q1为一个146×1组的矩阵;a1为一个10×1组的矩阵.
3.2 遗传计算法
遗传计算法(GA)为对自然界的生物进化体系进行模仿发展而来的随机性全局搜索及优化法,此为高效、并行且全局性搜索方法,搜索过程内可自动取得及积累相关搜索空间内的信息,且自适应性控制搜索全过程以此取得最优解[10].
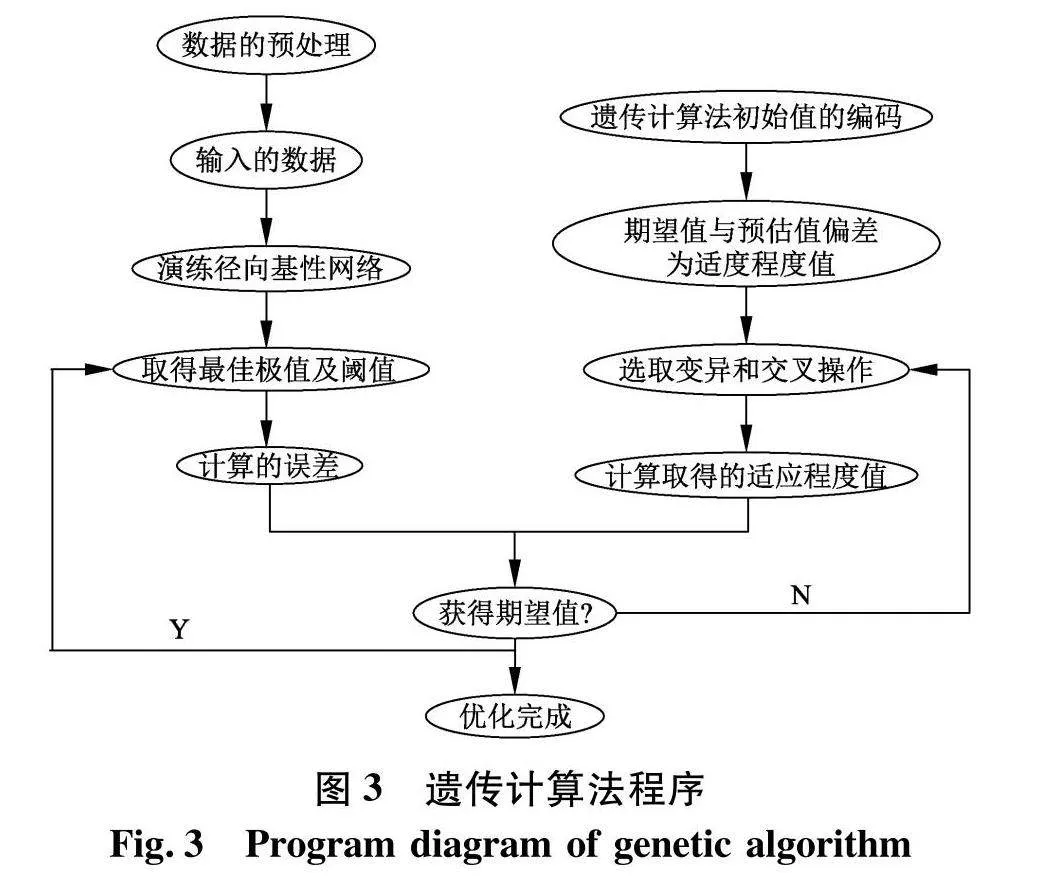
遗传计算法优化径向基的神经网络(RBF-GA)模型是经遗传计算法(GA)优化径向基(RBF)神经网络阈值及初始权值,以便优化取得的径向基(RBF)神经网络更方便预估函数输出.径向基的神经网络(RBF-GA)含有变异操作、交叉操作、选择操作、适应度函数和种群的初始化.在遗传计算法(GA)中,疑难候选解使用染色体来表示,完成解空间向的编码空间映射,其次使用随机数对一个种群进行初始化,编码即为种群内的个体[11],依据个体取得径向基神经网络阈值及初始权值,对网络预估输出及期望输出间误差的绝对值与G表示个体的适应度值p0利用选择函数进行优选选择,使个体基因进行变异,从而产生出子代,对上述程序重复操作,直至产生新种群,程序见图3.
其适应度的函数为:
p=h∑mj=1abs(yj-oj)(6)
式中:m为网络输出的节点数;yj为径向基(RBF)神经网络j节点期望输出;oj为j节点预估值;h为系数.
RBF-GA模型与RBF函数关系可各自表示为:
y2=Q2×exp-12ψ22‖X-a2‖(7)
ψ2=0.21,Q2=0.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 1…0.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.794 90.520 60.740 10.588 30.750 10.414 10.579 60.566 80.617 70.308 8,
a2=0.325 60.325 60.325 60.325 60.325 60.325 60.325 60.325 60.325 60.325 6
式中:Q2为一组146×7矩阵;a2为一组10×1矩阵.
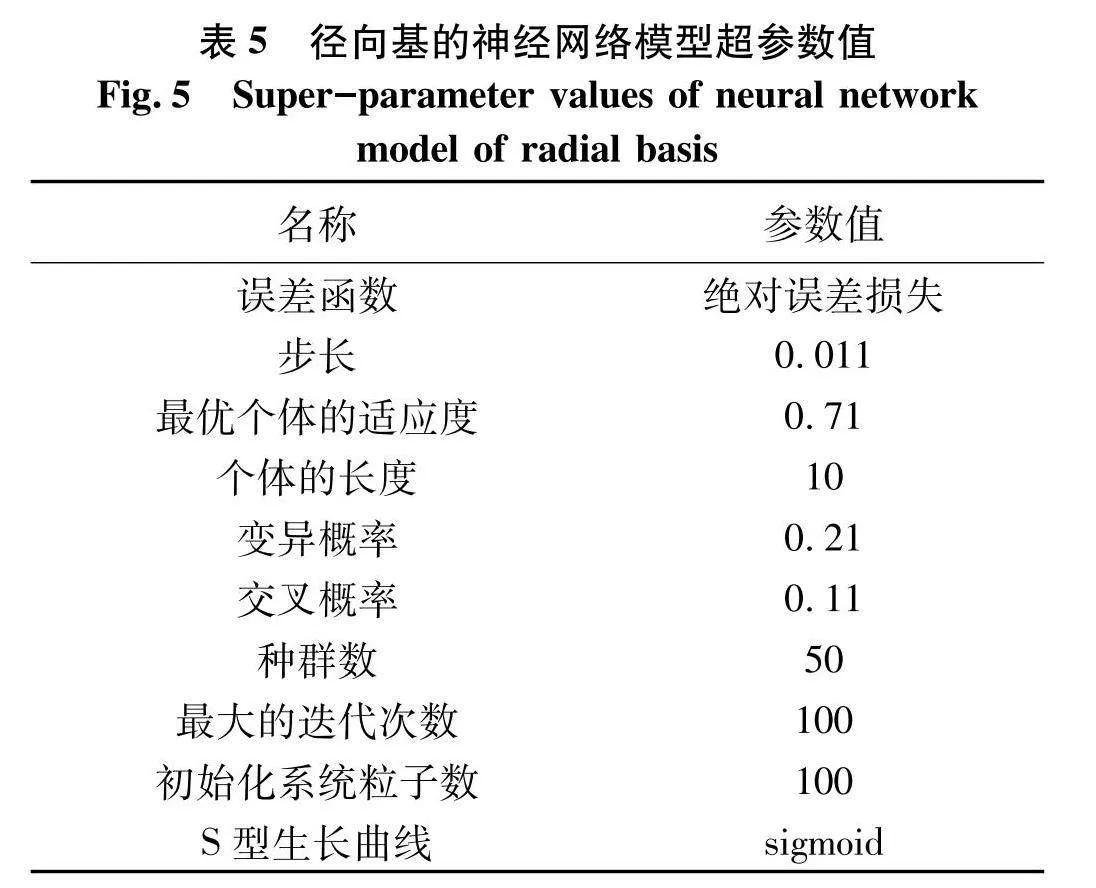
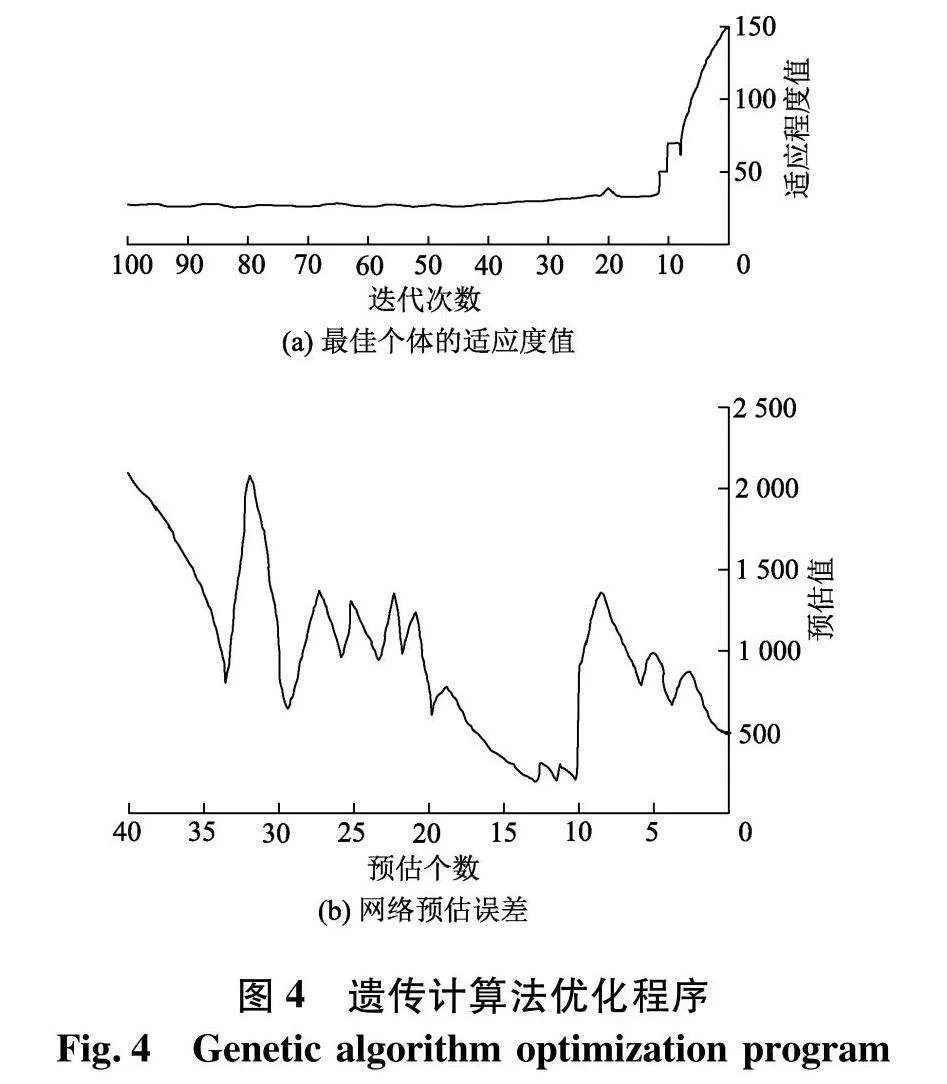
图4表示遗传计算法(GA)优化径向基(RBF)神经网络预估值和最优个体的适应度值间误差.图4(a)可知,遗传计算法(GA)优化中,随迭代次数增加适应度值迅速减小,迭代次数处于40左右渐趋于平缓,在迭代次数达100时可取得最优个体的适应度值,最大的迭代次数一般为100.图4(b)可知,预估样本为演练集合中选择的30组数据.图4(a)表示实验值,图4(b)表示预估值,由此可知,经遗传计算法(GA)模型优化取得的预估值和实验值非常近似,表明预估值具有较高的精度[12].表5为径向基的神经网络(RBF-GA)模型超参数值.
4 模型实验验证
4.1 某破冰船模型实验
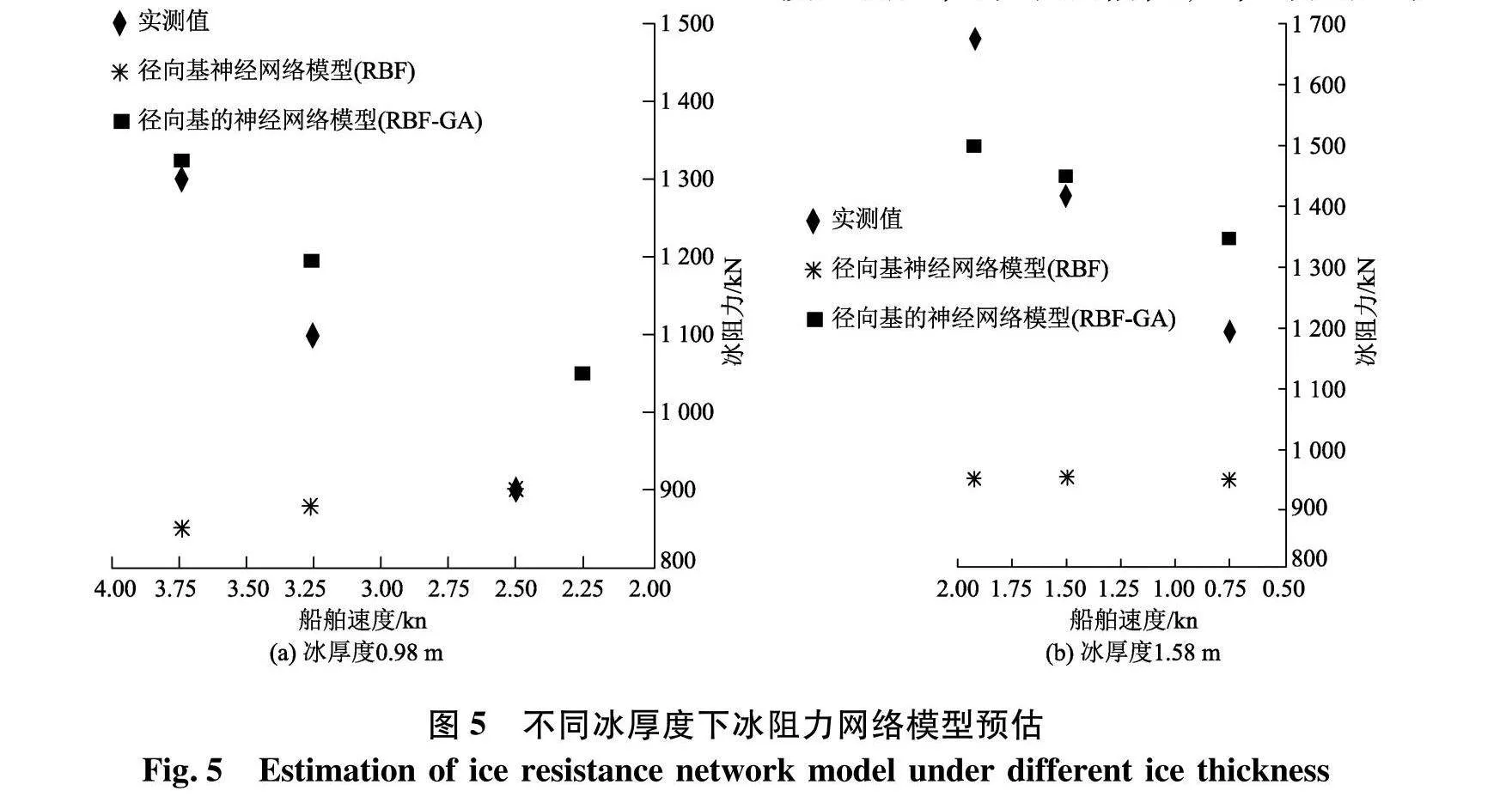
本研究选取一标准破冰船[8]作为研究目标,此船模型实验在给定两种冰厚度基础上进行,其冰厚度为0.98 m和1.58 m.图5表示按照比例尺放大冰阻力的测量值及径向基的神经网络、径向基神经网络模型预估的冰阻力.
从图5可知,径向基神经网络模型预估的冰阻力无明显变化,径向基的神经网络模型预估结果与船舶航行速度成正比关系.当冰厚度0.98 m时,径向基(RBF)神经网络模型测量值比预估值大较多,平均误差约15.6%,径向基的神经网络(RBF-GA)模型测量值小于预估值,平均误差约8.7%.当冰厚度1.58 m时,径向基神经网络模型预估值保持在951 kN,平均误差约32.6%,径向基的神经网络模型破冰船实测值与预估值基本一致,平均误差约7.3%.通过观察可知,在不同冰厚度下,随船舶航行速度增大,径向基的神经网络模型预估误差不大于8%,其预估精度比径向基神经网络模型有显著提高.
4.2 PSV破冰船模型实验
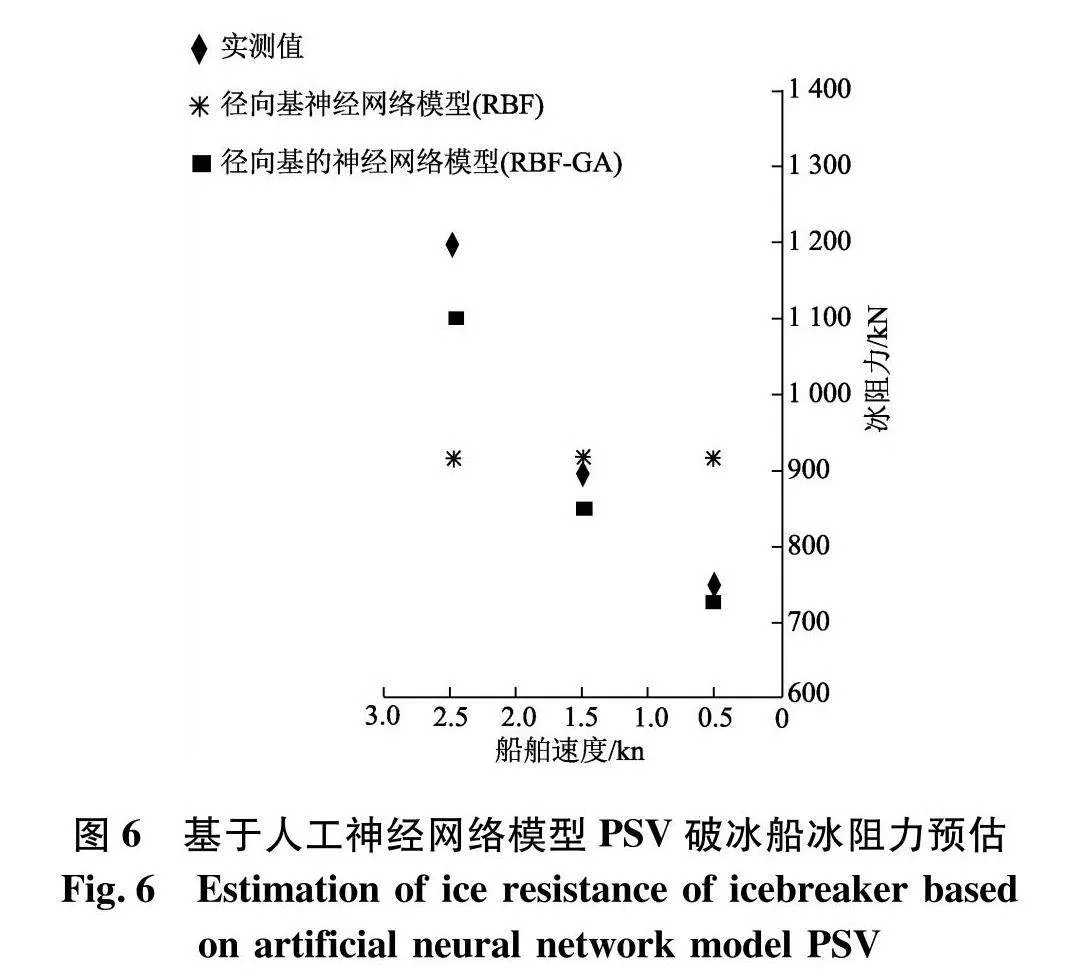
选取平台供应船(platform supply vessel,PSV)破冰船模型实验数据并作预估分析,按比例将数据进行全尺度放大,预估结果见图6.径向基的神经网络模型预估值和实测值非常接近,随着船舶航行速度增大,其破冰船实测值和预估值基本一致,预估值比较破冰船实测值可知,平均误差约8.3%,当船舶航行速度1 kn时,预估值和实测值几乎一致.当船舶航行速度小于1 kn时,此模型仍然适用.径向基神经网络模型冰阻力预估时,船舶航行速度增大,其预估值变化较小,比较实测值可知,平均误差约17.6%.
4.3 多用途破冰船实验验证
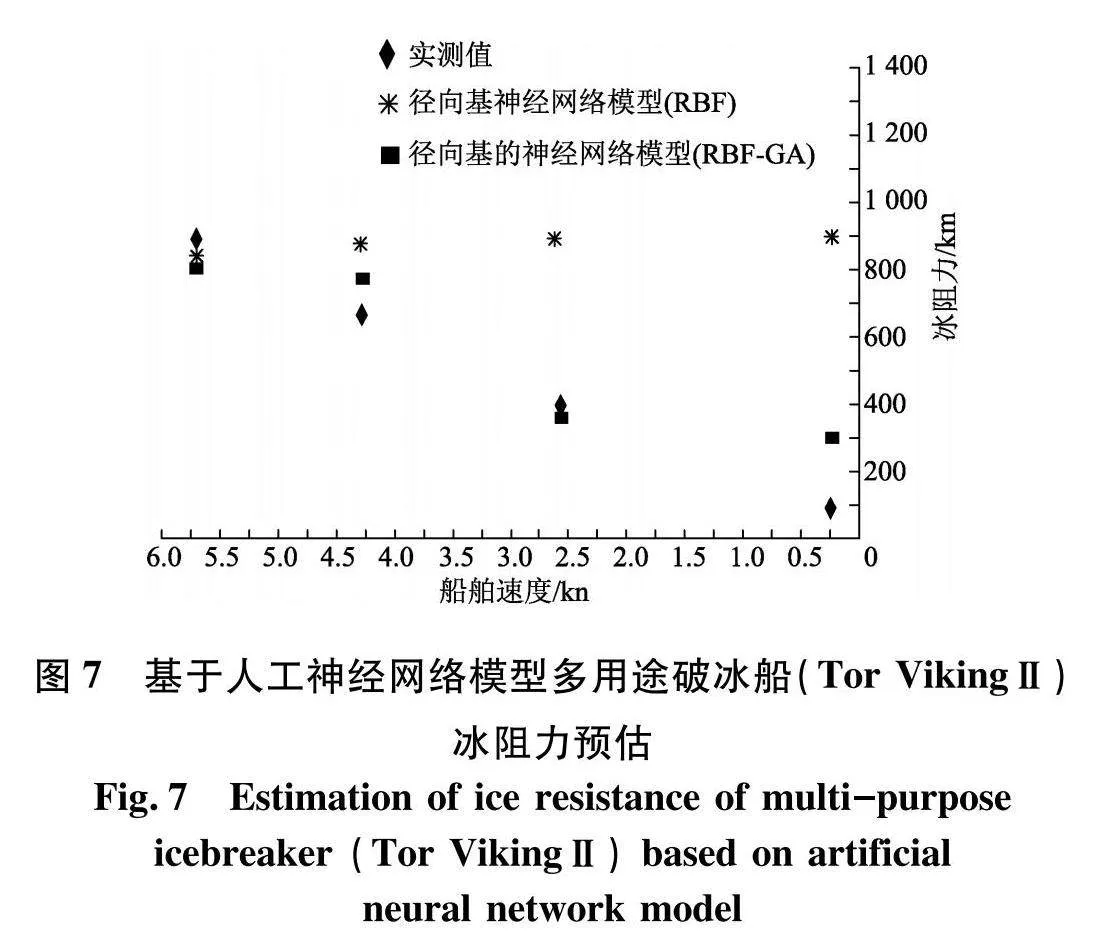
选取航经波罗的海的“Tor Viking Ⅱ”多用途型破冰船为例进行实验[7],将径向基神经网络模型和径向基的神经网络模型预估值和实测值对比并作出分析,见图7.
从图7可知,当船舶航行速度低于1 kn时,径向基神经网络模型和径向基的神经网络模型预估值比实测值大几倍之多,原因在于演练样本高度集中,船舶航行速度低于0~1 kn冰阻力的数据太少,从而模型在预估低速航行船舶冰阻力时,出现较大误差.随着船舶航速增大,两模型的预估值和实测值偏差也逐步减小,在船舶航行速度0.4~1.2 kn时,径向基神经网络模型预估值和实测值间平均误差约为12.0%,径向基的神经网络模型预估值和实测值较近似,平均误差约为7.5%.随着船舶航速增大,径向基神经网络模型预估值基本不变化,而径向基的神经网络模型预估值和实测值趋近于近似,从而证明了经遗传计算法优化后径向基神经网络模型对船舶航行速度敏感度强于未经优化的径向基经网络模型.
5 结论
文中提出了基于人工神经网络(ANN)极地船舶的冰阻力预估模型,分析了两个神经网络的预估法:径向基(RBF)神经网络模型方法和径向基的神经网络(RBF-GA)模型方法,并对两个预估模型和船舶模型实验及全尺度实验结果进行比较和分析,综合了冰厚度不同及船舶航行速度条件下模型预估结果,可得到径向基的神经网络(RBF-GA)模型泛化效果良好,对于船舶航行速度和冰厚度敏感度明显强于径向基(RBF)神经网络模型,可实现较精确预估冰阻力,平均误差不大于8%.在充足且可靠性强数据条件下,归一化特征量是确保每一特征权重处于可比范围中最关键环节,可确保预估结果可靠性和精度.因为数据库内有大量平整冰环境下船舶实验数据,从而平整冰环境下神经网络模型预估结果更精准.船舶在航行速度较低时,预估误差最大,因为演练样本缺乏船舶低速航行实验数据.冰阻力与船舶航行速度间皮尔逊关联系数较小,但不说明船舶航行速度对冰阻力影响较小.皮尔逊关联系数仅权衡线性关系,当系数为0,并不说明其无关联性.
参考文献(References)
[1] 王晓雪,张秀凤,刘兆春,等.航海模拟器中破冰船破冰阻力数值计算[J].哈尔滨工程大学学报,2024,45(1):204-212.
[2] 刚旭皓,田于逵,季少鹏,等.冰区船艏部连续破冰模式下破冰阻力数值计算研究[J].船舶力学,2022,26(7):969-977.
[3] 郑兴,田治宗,谢志刚,等.基于SPH方法的黄河破冰船冰阻力数值模拟分析[J].中国舰船研究,2022,17(3):49-57,84.
[4] 杨碧野. 碎冰区船舶冰阻力的预报方法及影响规律研究[D].大连:大连理工大学,2023.
[5] 黄焱,蒋瀚锋,孙剑桥.艉部先行模式下船舶冰阻力试验预报方法研究[J].中国造船,2023,64(3):23-32.
[6] 张健,李越,王颖凯.基于离散元法的碎冰区船舶航行冰阻力预报[J].舰船科学技术,2023,45(1):8-13.
[7] HUANG Y, HUANG S, SUN J. Experiments on navigating resistance of an icebreaker in snow covered level ice[J]. Cold Regions Science and Technology, 2018, 152:1-14.
[8] HU J, ZHOU L. Experimental and numerical study on ice resistance for icebreaking vessels[J]. International Journal of" Naval" Architecture and Ocean Engineering, 2015, 7: 626-639.
[9] ZHOU L, DIAO F, SONG M, et al. Calculation methods of icebreaking capability for a double-acting polar ship[J]. Journal of" Marine Science and Engineering, 2020, 8:179.
[10] YANG Y, TU H, SONG L, et al. Research on accurate prediction of the container ship resistance by RBFNN and other machine learning algorithms[J].Journal of Marine Science and Engineering,2021,9(4):376.
[11] ZHANG M, SUN Q, GARME K, et al. Analysis of inland waterway ship performance in ice: Operation time window[J]. Ocean Engineering, 2022, 263: 112409.
[12] 郑安宾,许汪歆,梁金雄,等.破冰船冰阻力经验模型分析[J].机电设备,2022,39(6):85-89.
(责任编辑:曹莉)
