基于混合RANS-LES方法的三维U型弯管内部流场数值模拟
2024-01-11郑家乐韩盼盼尤云祥冯爱春张瑞瑞







摘 要: 以三维U型弯管内部复杂的流动为对象,分别采用IDDES、SBES以及曲率修正后的SBES模型对弯管中的流动进行了数值模拟,对比分析了轴向速度、摩擦阻力系数和压力系数的试验和数值模拟结果.研究表明,SBES模型相对于IDDES模型有更好的模拟精度,且SBES模型的三类亚格子尺度模型中,WALE模型可以更为准确地模拟三维U型弯管内部流场特征.同时,曲率修正对SBES模型所得的轴向速度、摩擦阻力系数和压力系数数值模拟结果都有一定的改善效果.
关键词: 三维U型弯管;曲率流动;混合RANS-LES方法;IDDES模型;SBES模型
中图分类号:O352"" 文献标志码:A"""" 文章编号:1673-4807(2024)06-037-07
收稿日期: 2023-10-18"" 修回日期: 2021-04-29
基金项目: 江苏科技大学科研启动基金项目
作者简介: 郑家乐(1998—),男,硕士研究生
*通信作者: 韩盼盼(1990—),男,博士,助理研究员,研究方向为计算流体力学.E-mail:hanpanpan@sjtu.edu.cn
引文格式: 郑家乐,韩盼盼,尤云祥,等.基于混合RANS-LES方法的三维U型弯管内部流场数值模拟[J].江苏科技大学学报(自然科学版),2024,38(6):37-43.DOI:10.20061/j.issn.1673-4807.2024.06.006.
Numerical simulation of internal flow in a three-dimensional
U-bend duct using hybrid RANS-LES method
ZHENG Jiale1,2, HAN Panpan1*, YOU Yunxiang1,2, FENG Aichun1,2, ZHANG Ruirui3
(1.State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
(2.Yazhou Bay Institute of Deepsea Technology, Shanghai Jiao Tong University, Sanya 572000, China)
(3.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212100, China)
Abstract:The complex internal flow in the three-dimensional U-bend duct is numerically investigated based on hybrid RANS-LES method. Three models are adopted, i.e. the IDDES model, the SBES model, and the SBES model employing curvature correction. The experimental and numerical results of axial velocity, frictional drag coefficient, and pressure coefficient are compared in detail, it is found that the SBES model yields more accurate results than the IDDES model, and WALE model characterizes the internal flow of the three-dimensional U-bend duct well compared with the other two sub-grid scale models. Moreover, the curvature correction employed by the SBES model improves the numerical results of axial velocity, fractional drag coefficient and pressure coefficient.
Key words:three-dimensional U-bend duct, curvature flow, hybrid RANS-LES method, IDDES model, SBES model
U型弯管广泛分布于潜艇的水平舵系统和动力系统中.弯管内部复杂的流动在流固耦合的作用下常常会导致管道系统产生严重的振动与噪声,这不仅影响管道系统的工作性能及寿命,振动所产生的噪声还会影响声纳对目标的听测和潜艇的作战能力、损害艇员身心健康[1].因此,研究U型弯管内复杂的流动状况对于管道系统减振降噪、提高潜艇安全具有重要意义.
准确预测U型弯管流动这类大曲率的复杂内流仍属于当前CFD领域的难题之一.即使是目前工程应用中最常用的雷诺时均(RANS) 模型,在复杂和大曲率的流动中的模拟准确性表现并不好,而大涡模拟(LES)等高精度方法由于计算耗费资源太大而尚难以应用于实际工程计算.鉴于此,混合RANS/LES方法得到了广泛发展及应用,它的基本思想是对整个流场进行分区,在近壁面采用RANS模拟,在其它区域采用LES模拟,进而使其网格量大幅低于LES方法,同时又具有相当的解析度.
目前,混合RANS/LES方法主要分为脱体涡模拟类方法(包括DES、DDES和IDDES等)[2-4]以及应力混合涡模拟(SBES)方法[5].脱体涡模拟类方法已被应用到各种复杂的分离流动模拟中,包括圆柱绕流[6]、高超声速球形舱绕流[7]以及船体流场分析[8]等.脱体涡模拟类方法虽然在很多高雷诺数分离流问题中得到成功的应用,但当边界层比较厚或者分离区较窄时会遇到一些问题,包括网格诱导非物理分离(GIS)以及RANS与LES转换区导致的“灰区”等.
SBES方法旨在克服脱体涡模拟类方法的这类缺陷,它通过屏蔽(混合)函数可以有效地防护RANS对壁面边界层区域的求解,进而抑制来自LES的影响,并通过改进定义网格长度尺度,使得在分离剪切层中可以更快地由RANS切换到LES求解流场结构.此外,SBES可以更灵活地选择现存的任何一种LES方法结合RANS计算流场.目前在发动机非定常热流模拟[9]、变矩器内部流场预测[10]和气缸扰流[11]等方面得到了成功应用.
CFD数值模拟的准确性在很大程度上取决于所采用的湍流模型,但到目前为止,对三维U型弯管内流这类大曲率流动中常用的湍流模型性能的系统研究还较少,亟需进一步开展深入研究.
为此,文中以U型弯管的详细试验数据为基础[12],基于商业软件Fluent,采用混合RANS-LES方法中目前应用最广泛的IDDES与SBES方法,对该三维U型弯管内部的流动进行了数值模拟,系统地分析这两种混合RANS-LES方法对三维U型弯管内部流动的预测能力.
1 理论模型
1.1 IDDES模型
改进的延迟分离尾流模拟(improved delayed detached eddy simulation,IDDES)模型属于一种增强型DES类模型,综合了LES和RANS的优点,在近壁面边界层区域采用 RANS 模型,而在湍流主流区采用 LES 模型,其LES部分的亚格子模型采用Smagorinsky-Lilly.当进行湍流模拟时,IDDES模型可以根据网格尺度在RANS和LES模型之间转换.基于SST模型的IDDES方法,表示为[4]:
kt+uikxi=Pk-k2/3LIDDES+xjν+σkνtkxj(1)
ωt+uiωxi=γνtPk-βω2+xjν+σωνtωxj+
21-F1σω2ωkxjωxj(2)
式中:νt为涡粘系数;LIDDES为IDDES的长度尺度,由下式确定:
LIDDES=fd·LRANS+1.0-fd·LLES(3)
LLES=CDESΔ,LRANS= kβ·ω(4)
CDES=CDES1·F1+CDES2·1-F1(5)
式中,Δ为LES的长度尺度,定义为:
Δ=min(maxCωdω,Cωhmax,hwn,hmax)(6)
式(1~6)中的其他参数详见文献[13].
1.2 SBES模型
应力混合涡模拟(stress-blended eddy simulation,SBES)模型通过应力混合的方法,实现在近壁面边界层区域采用 RANS模型,在远离壁面的主流区采用 LES 模型,即[14]:
τSBESij=fsτRANSij+1-fsτLESij(7)
式中:τSBESij,τRANSij和τLESij分别为SBES、RANS和LES的湍流应力张量;fs为屏蔽函数.通常情况下,LES模型与RANS模型都采用基于Boussinesq假设的涡粘系数模型,则可简化为:
νSBESt=fsνRANSt+1-fsνLESt(8)
SBES模型的RANS部分在文中采用SST模型,LES部分可选择任意一种亚格子模型,包括Smagorinsky Lilly、Dynamic Smagorinsky及WALE模型.通过使用屏蔽函数fs,SBES模型可以有效地屏蔽适用于RANS模型的边界层区域,同时在适用的情况下迅速转换到LES.
1.3 曲率修正模型
当充分发展的湍流流经弯曲管道时,最关键的问题就是流线曲率对湍流的影响.流线曲率对湍流的影响是由离心力引起.传统涡粘模型(EVM)的缺陷之一就是对曲率/旋转效应的不敏感.许多研究人员通过对输送方程中特定项的修改来实现提高传统湍流模型对旋转曲率效应的敏感度.文献[15]提出了一种曲率修正(curvature correction,CC)方法,并把这一修正方法应用到了SST模型当中[16],称为SST-CC模型,其通过对输送方程的产生项进行修正,从而使改进的SST k-ω模型对曲率/旋转敏感化,具体修改为:
kt+uikxi=Pk·fr-β*kω+xjν+σkνtkxj(9)
ωt+uiωxi=γνtPk-βω2+xjν+σωνtωxj+
21-F1σω2ωkxjωxj(10)
式中,fr为旋转系数,定义为:
fr=max0,1+Cscalefr-1(11)
fr=maxminfrotation,1.25,0(12)
frotation=1+cr12r*1+r*1-cr3tan-1cr2r-cr1(13)
式中:fr为旋转系数;Cscale为曲率修正影响因子;frotation为修正旋转系数.
式(12)中下限是出于稳定性考虑,上限是为了避免过度产生涡流粘度.数值1.25是考虑不同研究模型的折衷数值.Cscale与曲率修正强度有关,默认为1;附加经验常数cr1、cr2和cr3分别为1、2、1.
2 计算模型
2.1 模型与边界条件
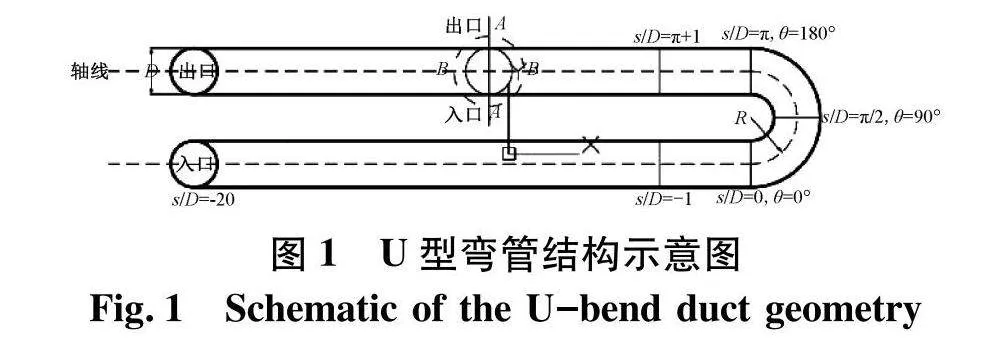
数值模拟研究所用三维U型弯管参数及试验数据均来自试验[12],U型管参数如图1.管的高度D=2a=76.2 mm,弯管处半径R=495.3 mm,入口段与出口段长度均为20D;水平方向AA连接管道的外壁面和内壁面;s为沿U型管中心线的自然坐标系,以入口段为原点,入口段为负,弯管处和出口段为正;角度θ用于定义沿弯管位置,以入口段与弯管交界处为0°.
根据Anwer文献提供的实验数据,选取入口段空气运动粘性系数ν=1.58×10-5 m2/s,入口流速W0=10.4 m/s,雷诺数Re=W0D/ν=5×104.分别测量了s/D=-1、θ=22.5°、θ=67.5°、θ=112.5°、θ=157.5°和s/D=π+1截面处沿水平方向AA的流体速度,以及从入口段到出口段管道内壁面与外壁面的表面摩擦阻力系数Cf和壁面压力系数Cp.
Cf和Cp定义为:
Cf=τw12ρW20, Cp=p-p012ρW20(14)
式中:τw为平均剪切应力;p为壁面静压力;p0为s/D=-18位置的壁面静压力;ρ为流体密度.数据来源试验台由内径D=76.2 mm的有机玻璃管组成,通过管道的气流由安装在试验台出口端的离心鼓风机提供.试验使用压力传感器测量了壁面压力,此外还测量了U型弯管的表面摩擦阻力和流动速度等参数.
为了比较不同混合RANS-LES模型对模拟结果的影响,采用IDDES模型、3种亚格子尺度模型下的SBES模型以及曲率修正后的SBES模型这些具有代表性的混合RANS-LES模型对三维U型弯管内的流动进行了计算.
2.2 网格设置
2.2.1 网格生成
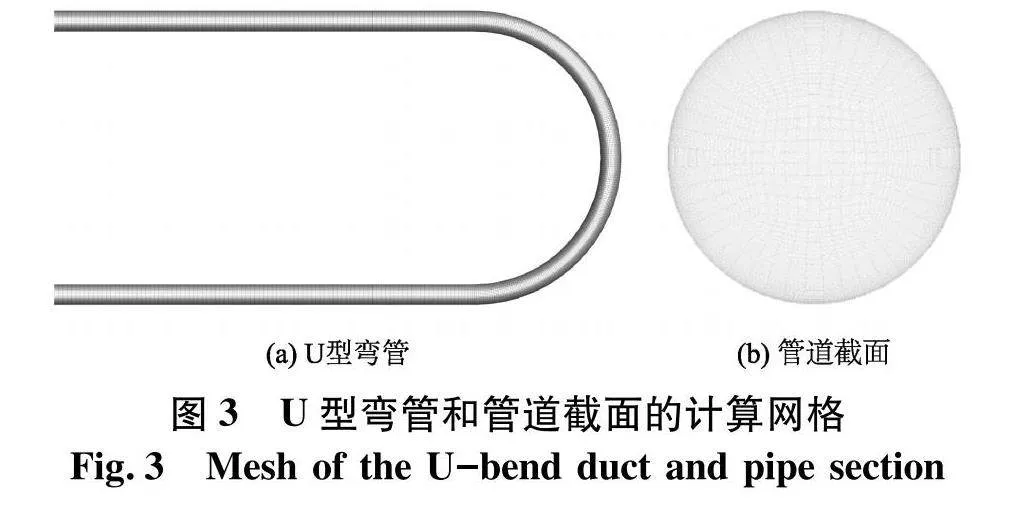
文中U型弯管网格的生成采用ANSYS WorkBench自带的网格绘制软件ICEM CFD来完成.整个U型弯管采用六面体结构化网格,对管道弯曲部分进行加密,并对弯管出入口段的网格采用渐变处理.同时,由于管道是圆柱体,在划分网格时应用了O型网格的方法以提高网格质量.
在对U型弯管内流动的计算中,混合RANS-LES模型须设置合适的网格,使该方法在近壁面特定区域内采用RANS模式,在远壁面采用LES模式,并在二者之间可使RANS模式及LES模式进行快速切换.对LES来讲,其对湍流场解析的能力与当地网格的滤波宽度Δ有关.结合相关文献[17-18]的结果,文中给出一个使LES在RANS/LES转化过程中即发挥其作用的条件为:
(dw/hmax)gt;1.6(15)
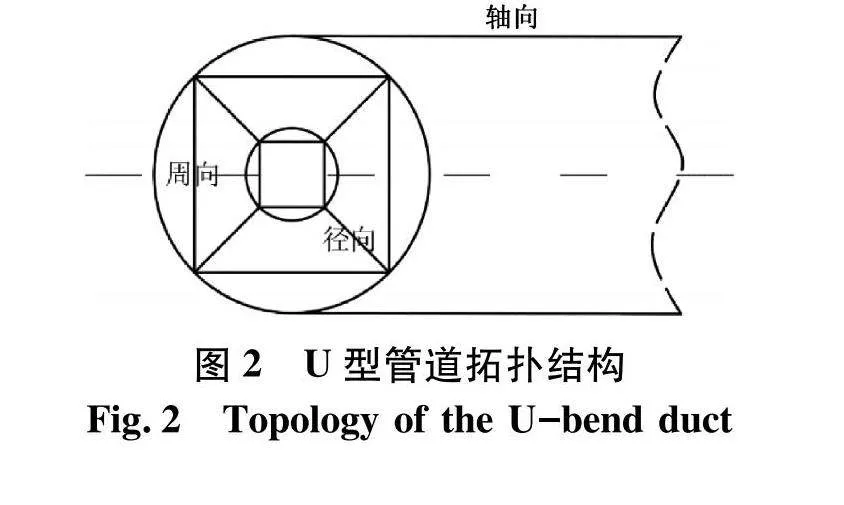
其中:dw为与壁面的距离;hmax=max{Δx,Δy,Δz}为当地网格的最大尺寸.对于U型弯管结构,其拓扑结构如图2,主要存在径向、周向与轴向3个方向.
为满足式(15),在设计网格时须使径向当地网格尺寸Δr、周向当地网格尺寸Δc以及轴向当地网格尺寸Δa满足式(15),即:
dw/Δrgt;1.6(16)
dw/Δcgt;1.6(17)
dw/Δagt;1.6(18)
根据上述要求,沿径向的网格布置采用“第一层网格+固定增长率”的方法,第一层网格y+=1.0,径向的网格增长率r=1.15,使得从第二个网格开始(包括第二个网格),径向的网格大小Δr都满足使LES在RANS/LES转化过程中即发挥其作用的条件式(15);沿周向的网格与沿径向的网格按照当地网格最大尺寸hmax=0.004 m进行布置,整个计算域的网格数约为4×106.划分后的U型弯管网格如图3.
2.2.2 网格无关性验证
为保证数值模拟结果的准确性,发挥湍流模型的最大优势,需要在计算前进行网格无关性验证.检验网格独立性时一般是比较不同密度网格计算的结果,如果相邻两次计算结果相差较大,则继续增加网格,如果误差在可接受的范围内,则认为网格数合适.一般来说,网格尺寸y+lt;2,才能满足增强壁面函数或者近壁面区域的要求,使得粘性亚层能够正常解析.
以管道轴向速度分布为验证对象,分别取θ=22.5°与θ=112.5°这两处弯管区域进行网格密度比较,结果如图4.
横轴r/a表示无量纲的径向坐标:纵轴W/W0表示无量纲的轴向速度.y+=1.5时网格数约为3.1×106个,y+=1.0时网格数约为4×106个,y+=0.5时网格数约为5.1×106个.速度计算结果显示,当y+=1时所得到的近壁区域网格密度就能够满足数值模拟的需要,这一结果验证了文中网格划分的合理性.
3 计算结果与分析
3.1 IDDES与SBES模型的计算结果
3.1.1 流向速度
图5为U型弯管各截面的速度沿其径向的分布曲线.横轴r/a表示无量纲的径向坐标:当r/a=-1时为U型弯管外侧壁面;当r/a=0时为轴线位置;当r/a=1时为U型弯管内侧壁面.纵轴W/W0表示无量纲的轴向速度.图5(a)为进入弯管前的截面,图5(f)为流出弯管后的截面,图5(b)~(e)为进入弯管后的不同截面,s/D及θ的定义见图1.由图可知,对于进入弯管前的流动,轴向速度分布关于轴线对称,进入弯管后,这种对称性逐渐消失,这说明在U型弯管的曲率影响下,管内的流动表现出一定的各向异性特性.
从图5(a、b)中可以看到,在入口段s/D=-1和θ=22.5°截面位置处,IDDES与SBES的模拟结果差异较小,且都大于试验值.对于θ=67.5°与θ=157.5°这两处弯管区域,如图5(c、e),各湍流模型的数值计算结果同试验结果有明显的差异,其中SBES模型在轴线外侧区域的数值计算结果与试验值较为接近,在内侧区域的数值计算结果较差,而IDDES模型在两侧的数值计算结果都同试验值偏差较大.在θ=112.5°以及s/D=π+1截面处,IDDES模型与SBES模型的数值计算结果都与试验值较为吻合,SBES模型略优.整体来说,SBES模型的数值计算结果同试验更为接近.
3.1.2 表面摩擦阻力系数和壁面压力系数
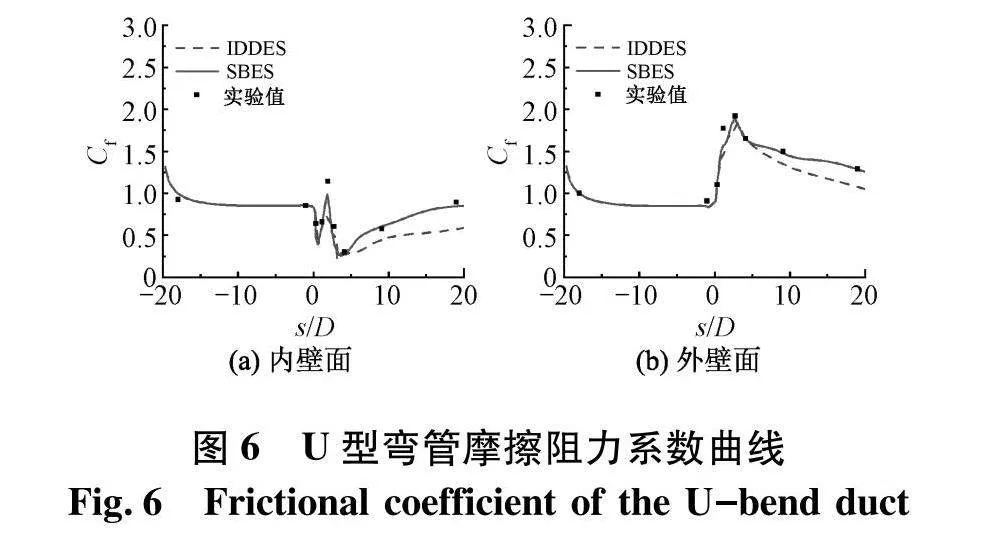
图6为内外壁面表面摩擦阻力系数Cf的变化曲线,当流动接近弯曲段时,内侧壁面处的轴向速度梯度减小,表面摩擦阻力系数Cf也随之降低,直到θ=90°附近,速度梯度增加,Cf也逐渐增加,并在θ=110°附近达到峰值之后再次减少,随后逐渐恢复.从图6(a)中可以看到,SBES模型在弯曲段的摩擦阻力系数峰值大于IDDES模型,但都小于试验结果.外壁面摩擦阻力系数Cf的变化情况与内壁面相反,Cf随着弯管前半段流速度梯度的增加而快速增加,随着后半段速度梯度的降低而快速减少.各湍流模型预测的峰值大小都低于试验结果的同时,峰值位置都比试验结果推后,如图6(b).对于下游摩擦阻力系数的预测,SBES模型的模拟结果都与试验值吻合较好,而IDDES模型则有着较大偏差.
除了表面摩擦阻力系数Cf以外,壁面压力系数Cp在工程中也是非常重要的参数.受弯管曲率影响,内外壁面在s/D=-5附近便会有明显的压差产生,而在弯管下游同样的距离,即s/D=π+5附近,下游的Cp变化曲线与上游变化曲线紧密平行,意味着管道流恢复到完全展开的直管状态.图7为各湍流模型在壁面处的压力系数绝对值.由图可见,各湍流模型的模拟结果都较为准确,SBES模型对于下游壁面压力系数Cp的预测与试验更为吻合.
3.2 SBES亚格子模型及曲率修正的影响
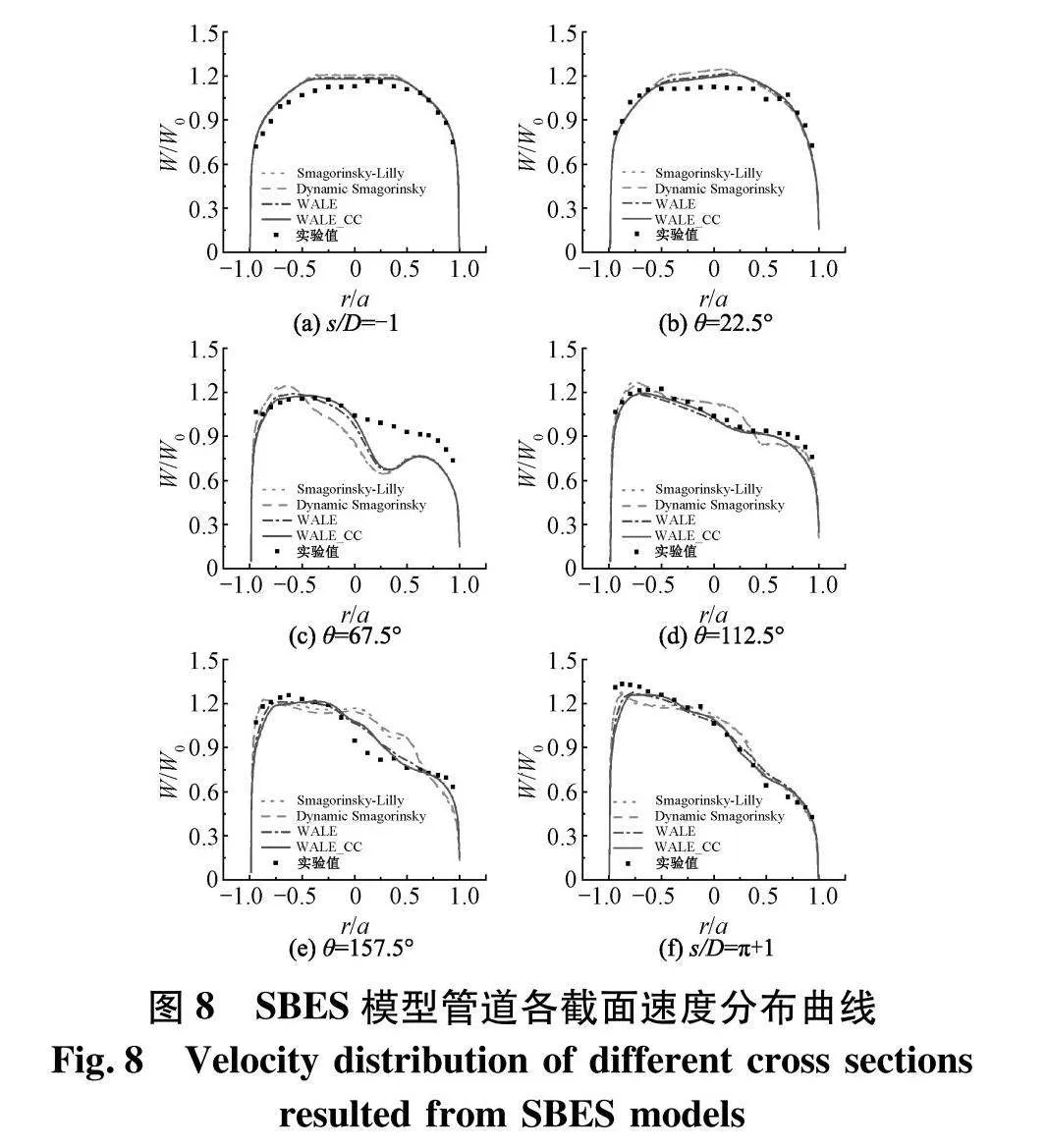
由上文的分析可知,在同样使用Smagorinsky-Lilly亚格子模型的条件下,SBES模型对U型弯管内部复杂流动的预测比IDDES模型更加精准.除Smagorinsky-Lilly亚格子模型外,SBES还可选用更加先进的亚格子模型Dynamic Smagorinsky及WALE.另外,对于三维U型弯管内流这类大曲率流动还应考虑旋转曲率效应的影响.为此,对SBES的3种亚格子模型的影响开展研究,并采用优选的亚格子模型分析了曲率修正的作用.
从图8中可以看出,相对于Smagorinsky-Lilly与Dynamic Smagorinsky模型,WALE模型在U型弯管各截面处的速度分布模拟结果都与试验更加吻合,尤其是在弯管中部θ=112.5°与θ=157.5°这两处位置,3种亚格子尺度模型的模拟结果差异更加明显;整体来看,对于速度分布数值计算结果,经过曲率修正后的WALE_CC模型比原WALE模型的数值计算略好一些,说明对于三维U型弯管流动,曲率修正对SBES方法的预测性能具有一定的改善效果.
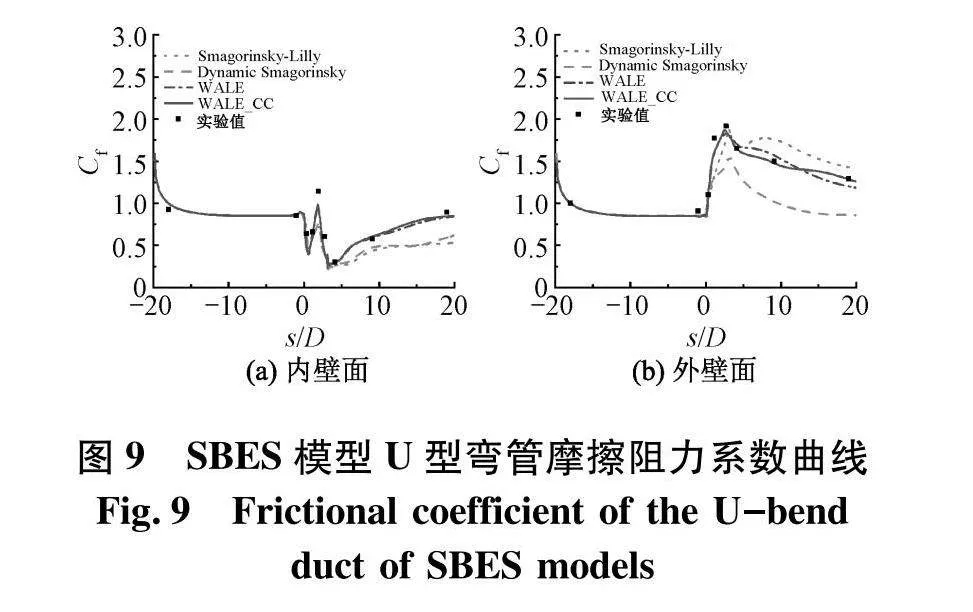
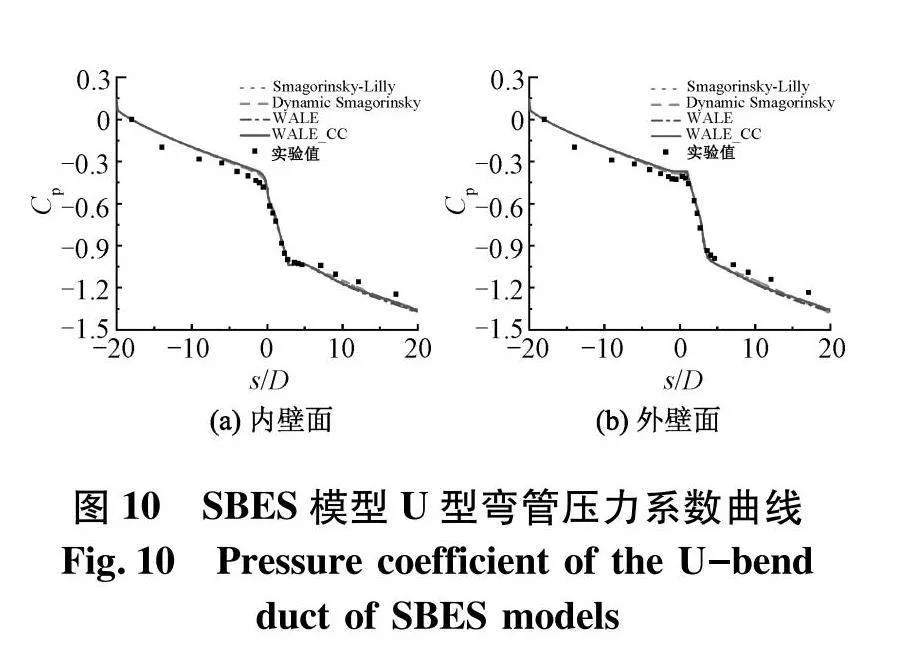
图9、10分别为基于SBES模型计算得的壁面摩擦阻力系数曲线以及壁面压力系数曲线.由图可知,WALE模型与试验值最为吻合;曲率修正CC对于WALE模型同样具有一定的正面效果.对于内外壁面的压力系数,各湍流模型的模拟结果差距很小且都较为准确.
综合以上对比可知,对于SBES方法,3种亚格子尺度模型中WALE模型的计算结果最优且曲率修正对于计算结果的改善起到了一定的优化作用.
4 结论
针对三维U型弯管内的流动问题,采用混合RANS-LES方法中应用广泛的IDDES与SBES方法,通过数值计算结果与试验结果对比,综合分析了对三维U型弯管内复杂流动的预测能力.在此基础上,针对SBES方法,进一步分析了不同亚格子模型及旋转曲率修正对计算结果的影响.
(1) IDDES方法及SBES方法均能较好模拟三维U型管内流动,二者的轴向速度在θ=67.5°与θ=157.5°位置与试验值相差较大,外壁面摩擦阻力系数的峰值与试验结果存在着一定偏差.整体来说,SBES方法相对于IDDES方法有更高的精度.
(2) SBES模型的3种亚格子模型中,WALE模型的结果与试验结果吻合较好,可更为准确模拟三维U型弯管内部流场特征.
(3) U型弯管内部流动受旋转曲率效应的影响,经过曲率修正的SBES模型相较于原始SBES模型具有优化效果.
参考文献(References)
[1] 孔建益, 李公法, 侯宇.潜艇振动噪声的控制研究[J]. 噪声与振动控制,2006(5) :1-4,17.
[2] SPALART P, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings "and on a hybrid RANS/LES approach[C]∥Advances in DNS/LES. Columbus, OH,USA:Greyden Press,1997.
[3] SPALART P R, DECK S, SHUR M L, et al.A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006,20(3):181-195.
[4] SHUR M L, SPALART P R, STRELETS M K, et al.A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J].International Journal of Heat and Fluid Flow,2008,29(6):1638-1649.
[5] MENTER F. Stress-blended eddy simulation (SBES)—a new paradigm in hybrid RANS-LES modeling in progress in hybrid RANS-LES modelling[J].Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 2018, 3: 27-37.
[6] 唐虎, 常士楠, 成竹,等.亚临界圆柱绕流的DES方法比较[J]. 航空学报, 2017,38(3): 92-102.
[7] LI C, GUO Q L, SUN D, et al. Aerothermal prediction of hypersonic flow around spherical capsule model using IDDES approach[J]. Intertnational Journal of Modern Physics, 2020, 34: 14-16.
[8] 尹崇宏, 吴建威, 万德成.基于IDDES方法的模型尺度和实尺度VLCC阻力预报与流场分析[J].水动力学研究与进展(A辑), 2017, 31(3): 259-268.
[9] GUO L X, ZHAO D, XU J Y,et al.Predicting unsteady heat-fluid interaction features and nonlinear acoustic behaviors in standing-wave thermoacoustic engines using unsteady RANS, LES and hybrid URANS/LES methods[J]. International Communications in Heat and Mass Transfer, 2023,142: 106617.
[10] 鄢万斌,杨孔华.基于动态混合RANS/LES模型的液力变矩器内部流场的数值模拟[J]. 吉林大学学报(工学版), 2023, 54(4): 926-937.
[11] DOROGI D, BARANYI L. Identification of upper branch for vortex-induced vibration of a circular cylinder at Re=300[J]. Journal of Fluids and Structures,2020,98(6):103135.
[12] SO R M C, ANWER M. Swirling turbulent flow through a curved pipe[J]. Experiments in Fluids, 1993,14(1/2):85-96.
[13] GRITSKEVICH M S, GARBARBARUK A V, SCHUTZE J, et al. Development of DDES and IDDES formulations for the k-ω shear stress transport model[J]. Flow Turbulence and Combustion,2011,88(3):431-449.
[14] REZAEIHA A, MONTAZERI H, BLOCKEN B.CFD analysis of dynamic stall on vertical axis wind turbines using scale-adaptive simulation (SAS): Comparison against URANS and hybrid RANS/LES[J]. Energy Conversion and Management, 2019,196:1282-1298.
[15] SPALART P R, SHUR M. On the sensitization of turbulence models to rotation and curvature[J]. Aerospace Science and Technology, 1997,1(5): 297-302.
[16] SMIRNOV P E, MENTER F R.Sensitization of the SST turbulence model to rotation and curvature by applying the spalart-shur correction term[J].Journal of Turbomachinery, 2009, 131(4): 041010.1-041010.8.
[17] KAEAI S, LARSSON J.Wall-modeling in large eddy simulation: Length scales, grid resolution and accuracy[J]. Physics of Fluids, 2012, 24(1):015105.
[18] HAN Y, HE Y, LE J. Modification to improved delayed detached-eddy simulation regarding the log-layer mismatch[J].AIAA Journal, 2020,58(2): 712-721.
(责任编辑:贡洪殿)
