风浪荷载作用下导管架结构的损伤识别研究
2024-01-11袁平平程雪莉张健





摘 要: 为了对导管架结构进行损伤定位和损伤量化,引入一种基于变分模态分解(variational mode decomposition, VMD)和Chirplet变换(Chirplet transform, CT)的损伤识别方法.采用导管架结构模型进行模拟,设置规则波浪荷载、不规则波浪荷载和风荷载3种环境荷载来模拟导管架真实环境,提取损伤杆件各节点的加速度响应信号,采用所提方法分析损伤前后能量变化,进行损伤定位,计算损伤位置处的时频熵进行损伤量化.设置不同工况验证了所提方法的可行性,结果表明,所述方法可以在不同环境荷载作用下对导管架进行损伤定位和损伤程度量化.
关键词: 导管架结构;变分模态分解;Chirplet变换;损伤定位;损伤量化
中图分类号:U655.55+1;TU311.3"" 文献标志码:A"""" 文章编号:1673-4807(2024)06-014-08
收稿日期: 2023-06-29"" 修回日期: 2021-04-29
基金项目: 国家自然科学基金面上项目(51979130);江苏省博士后科研计划项目(2021K562C)
作者简介: 袁平平(1989—),男,博士,副教授,研究方向为工程结构参数识别、损伤识别、模型修正.E-mail:yuanpingping@just.edu.cn
引文格式: 袁平平, 程雪莉,张健,等.风浪荷载作用下导管架结构的损伤识别研究[J].江苏科技大学学报(自然科学版),2024,38(6):14-21.DOI:10.20061/j.issn.1673-4807.2024.06.003.
Research on damage detection of jacket structure under wind and wave loads
YUAN Pingping1, CHENG Xueli2, ZHANG Jian2
(1.School of Civil Engineering and Architecture, Jiangsu University of Science and Technology, Zhenjiang 212100, China)
(2.School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212100, China)
Abstract:In order to conduct damage localization and damage quantification of jacket structure, a new damage detection method based on variational mode decomposition (VMD) and Chirplet transform (CT) is introduced. Three kinds of environmental loads, namely regular wave load, irregular wave load and wind load, are set on the jacket structure to simulate the real environment of the jacket. The acceleration response signals of each node of the damaged rod are extracted, and the proposed method is used to analyze the energy changes before and after damage for damage localization. Then, the time-frequency entropy of the damage location is further calculated for damage quantification. The feasibility of the introduced method is verified by setting different operating conditions, and the results show that the introduced method can locate and quantify the damage of the jacket under different environmental loads.
Key words:jacket structure, variational mode decomposition, Chirplet transform, damage localization, damage quantification
长期处于风、波浪等工作环境条件下,导管架结构不可避免地会受到不同类型、程度的损伤,比较典型的损伤有疲劳裂纹、腐蚀缺陷和断裂等.导管架结构的局部微小损伤往往会导致结构的单个或者多个部件产生损坏.随着使用寿命的增加,这些微小损伤在结构构件中逐渐扩大,导致构件或整个结构面临失效,无法正常作业.在导管架这种大型结构上,一般是由微小的损伤演变成大面积的破坏,如果没有及时的发现和加固处理不仅会造成经济损失也会对人员的安全造成威胁.文献[1]采用小波变换和神经网络对海洋平台结构进行了损伤识别与定位,采用位于墨西哥湾海域的一个导管架模型进行分析,验证了所提方法的可行性.文献[2]提出了基于振动传递率的钢质导管架海洋平台结构损伤识别方法,文中以导管架为模型,考虑高斯白噪声影响下,振动传递率函数和BP神经网络的损伤识别结果,并做了相关的试验验证.文献[3]提出了基于应力变化的损伤识别方法,并以某石油生产平台等比例模型为研究对象,研究了不同损伤程度及不同损伤位置的工况,并考虑了冲刷和腐蚀对损伤识别的影响.文献[4]提出了一种新的应变扩展-减量方法识别海上导管架子结构的多重局部损伤,并采用数值模拟和试验验证了该方法的可行性.文献[5]提出了基于模态应变能的海洋平台结构损伤识别,综述了几种与模态应变能相关的损伤识别技术,即损伤指数法、模态应变能变化法、跨模态应变能法和其他方法.该文献对4种典型的模态应变能相关方法进行了概述,结合数值模拟和实验数据系统地研究了一维梁和三维海洋平台结构的损伤识别问题,考虑了空间不完备性、噪声污染等问题,比较了4种方法的损伤定位能力.文中结合变分模态分解(variational mode decomposition,VMD)和Chirplet变换(Chirplet transform,CT),引入一种基于VMD和CT的导管架结构损伤识别方法.首先,采用VMD进行多分量信号分解[6],得到模态分量(intrinsic mode function,IMF);其次,对各个模态分量进行CT变换,计算各模态分量的能量,与未损伤状态下模态分量的能量对比,从而判断结构是否损伤并进行损伤定位;然后,再分别计算各阶模态分量的时频熵,判断结构的损伤程度;最后,通过不同工况下的导管架结构数值模拟验证所提方法的可行性.
1 理论基础
1.1 Airy波荷载
Airy波亦称为微幅波理论或线性波理论,其利用势函数来研究波浪运动,Airy波的波面方程为:
η(x,t)=H2cos(kx-ωt)(1)
k=2πL(2)
θ=kx-ωt(3)
式中:H为规则波波高;k为规则波波数;L为规则波波长;ω为规则波高频率;x和θ分别为波浪的相对位置和相位.
Airy波的速度势函数为:
φ(x,z,t)=Hω2k cos [k(z+d)]sin(kd)sin(kx-ωt)(4)
式中:d为水深;z为圆柱段所处水深.
Airy波的色散关系式为:
L=gT22πtanh(kd)=gT22πtan2πLd(5)
式中,T为波浪周期.
水质点的水平速度和垂直速度分别为:
ux=φx=πHTcosh[k(z+d)]sinh(kd)cos(kx-ωt)(6)
uz=φz=πHTsinh[k(z+d)]sinh(kd)sin(kx-ωt)(7)
水平加速度和垂直加速度分别为:
ax=2π2HT2cosh[k(z+d)]sinh(kd)sin(kx-ωt)(8)
az=2π2HT2sinh[k(z+d)]sinh(kd)cos (kx-ωt)(9)
1.2 不规则波浪荷载
在真实海域里,波浪并不完全是规则波,而是较为复杂的随机波浪[7].文中采用Stokes理论[8],其自由表面的运动和动力边界条件都是非线性的,Stokes五阶波理论的基本特征如下.
波长为:
L=gT2tanh(kd)2π=gT22π·sc1+πHL8c4-4c2+58s4(10)
式中:c=cosh(kd),s=sinh(kd).
波形为:
η=H2cos θ+(πH8L)2c(2c2+1)s3cos(2θ)(11)
水平方向水质点的速度为:
u=HgT22L·1ccosh(kξ)cos-1θ+
34(πHL)2cs4cos(2kξ)cos(2θ)(12)
式中,ξ=z+d.
垂直方向水质点的速度为:
v=cπHL·1ssinh(kξ) sin θ+34πHL21s4sin(2kξ) sin(2θ)(13)
水平方向水质点的加速度为:
ut=gπTL·1ccosh(kξ) sin θ+
3πTπHL2cs4cos(2kξ)sin(2θ)(14)
垂直方向水质点的加速度为:
vt=2πcT·1cπHL·1ssin(kξ) cos θ+32πHL21s4sin(2kξ)cos(2θ)(15)
1.3 风荷载
导管架在工作中面临着许多复杂的荷载,风荷载就是其中一种对导管架平台影响较大的荷载.在海面风场中,风速一般由定常风和脉动风两部分组成.文中采用美国石油协会API [9]规范给出的风荷载公式进行计算:
F=ρ2CsV2A(16)
式中:ρ为空气密度;Cs为结构形状系数;V为平均风速;A为与风向垂直的构件受风面积.
1.4 变分模态分解
VMD是一种信号分解估计方法,其整体框架是变分问题,它通过迭代搜寻有限的带宽和匹配最佳的中心频率,使每个模态的估计带宽最小.该方法可以确定本征模态分量的个数,并根据实际情况控制输出本征模态分量的个数,每个IMF为:
Uk=Ak(t)cos[φk(t)](17)
式中:Ak(t)为Uk的瞬时幅值;φk(t)为瞬时相位;t为时间.
1.5 基于能量指标的损伤定位
当结构产生损伤时,其损伤位置处的参数会发生变化,因此可以对比分析结构损伤前后的参数从而进行损伤定位.首先,对结构响应信号进行VMD分解,将其分解成一系列单分量信号,然后,再采用CT对各个模态分量分析,引入相应的能量指标[10]进行损伤定位.对模态分量进行CT变换,其系数为CTx(ti,fj),则该分量的CT能量可表示为:
Exj=∫T0CTx(ti,fj)2dt=∑ni=1CTx(ti,fj)2(18)
因此,各个模态分量的总能量为:
Ex=∑mj=1Exj(19)
将损伤前后的CT总能量分别表示为Eux和Edx,则归一化后的CT总能量变化为:
ΔEx=Edx-EuxEux=EdxEux-1(20)
由上式可知,当ΔEx由零变成正值时,即表明结构产生了损伤.静定结构发生损伤可以看作结构发生软化,超静定结构发生损伤通常会发生内力重分布.内力重分布的机理复杂,无法像静定结构得到类似的损伤结论,但对于没有过多约束的超静定结构,结构软化理论是可以接受的[11].因此Edx通常是大于Eux的,且比值越大表明该位置处发生损伤的可能性越大.
1.6 基于时频熵的损伤量化
为了定量能量变化,引入时频熵[12-14],将时频图平面按照时间和频率分成若干个面积相等的区域块,每个区域块的能量记为Ei,时频图的总能量为A,对每个区域块的能量进行归一化[15]处理,即qi=Ei/A,则时频图的时频熵可表示为:
S(q)=-∑N1qilnqi(21)
根据熵[16]的性质可知,CT时频图的能量分布越均匀,即在更多的区域中存在能量分布,时频熵值越小,反之,熵值越大.时频熵大多用于机械故障诊断,文献[17]采用Winger谱时频熵对齿轮故障进行判断,文中时频熵值随着故障程度的增加不断增大,采用最小二乘法拟合了故障程度和熵值之间的关系.
2 导管架模型
对导管架平台数值算例进行分析,针对不同位置、不同程度的损伤情况进行有限元计算和损伤识别.导管架主要由两部分组成,即导管架主桩腿和导管架支撑构建,导管架支撑构建由立柱、水平撑杆和斜撑杆组成,整个平台共有1 258个单元,设有两层甲板,甲板高程为6 m,桩腿有5°左右的倾斜,为了简化计算,文中未考虑土层对平台的影响,也不考虑附加水质量的影响.
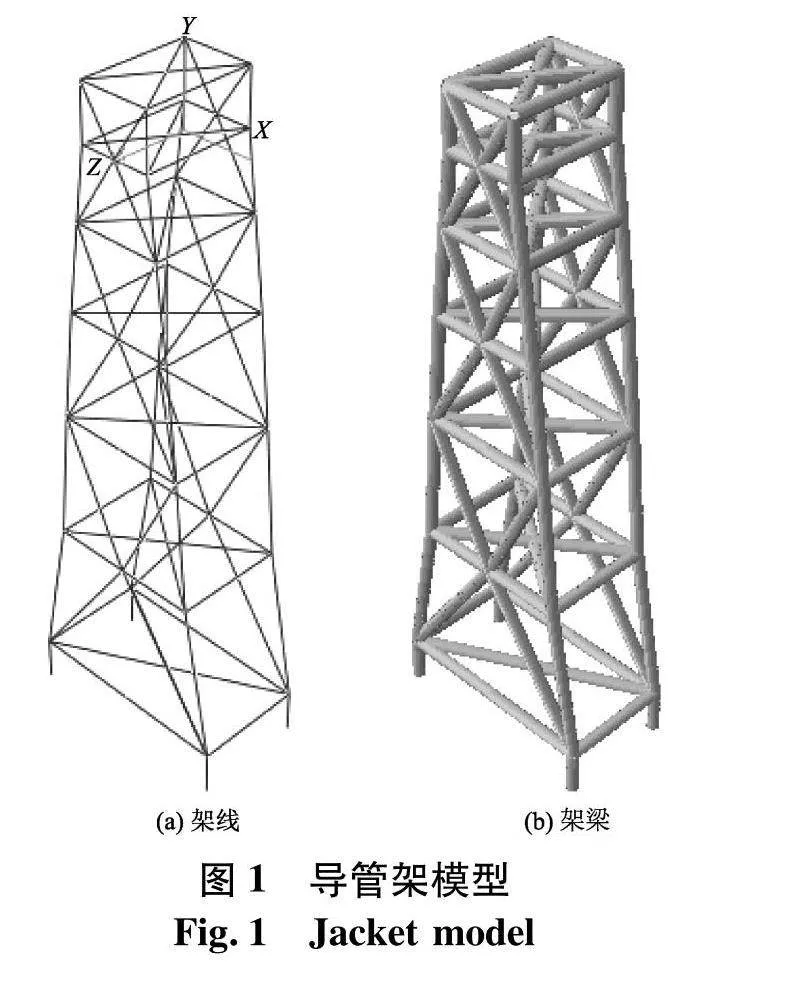
算例中,平台高度75 m,在ABAQUS软件中,首先建立导管架的线模型轮廓,在属性模块里面赋予导管架材料密度、杨氏模量、泊松比.导管架采用钢材,密度为7 850 kg/m3,弹性模量为2×1011 Pa,泊松比为0.3.设定杆件的切线方向,并对桩腿、斜撑、横撑等进行截面形状及尺寸的设置,管径为1.372 m,壁厚0.038 m,在装配模块中进行装配,装配完成的导管架模型如图1.
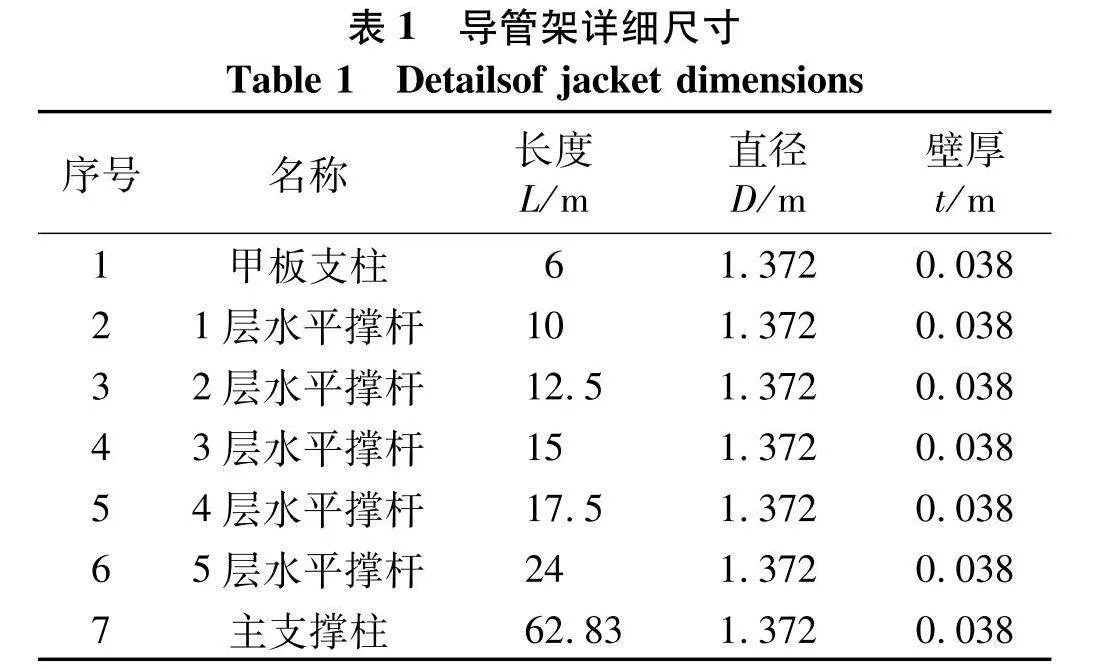
导管架海洋平台有5层水平支撑杆、甲板支柱、主支撑柱,具体详细尺寸如表1,因为导管架之间的间距比较大,故相邻之间的群桩效应可忽略不计,整个模型重1 559.80 t.
3 风浪荷载下导管架损伤识别
3.1 规则波浪荷载下损伤识别
水深d=9 m,采用Airy波,波高H=0.5 m,波长λ=3 m,波浪周期为T=3 s,邱卡数KClt;5,惯性力系数取CM=2.0,拖曳力系数取CD=1.2.
3.1.1 密集单元损伤识别
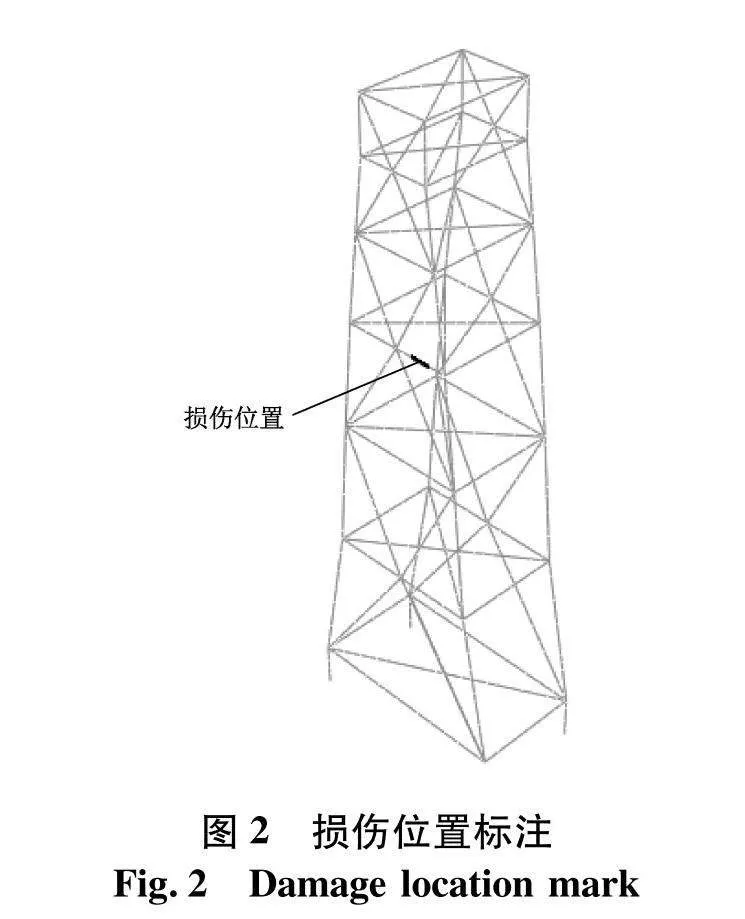
为了判断规则波浪荷载下所提方法是否能判断管件密集单元损伤位置及损伤程度,工况设置如表2,损伤单元见图2.
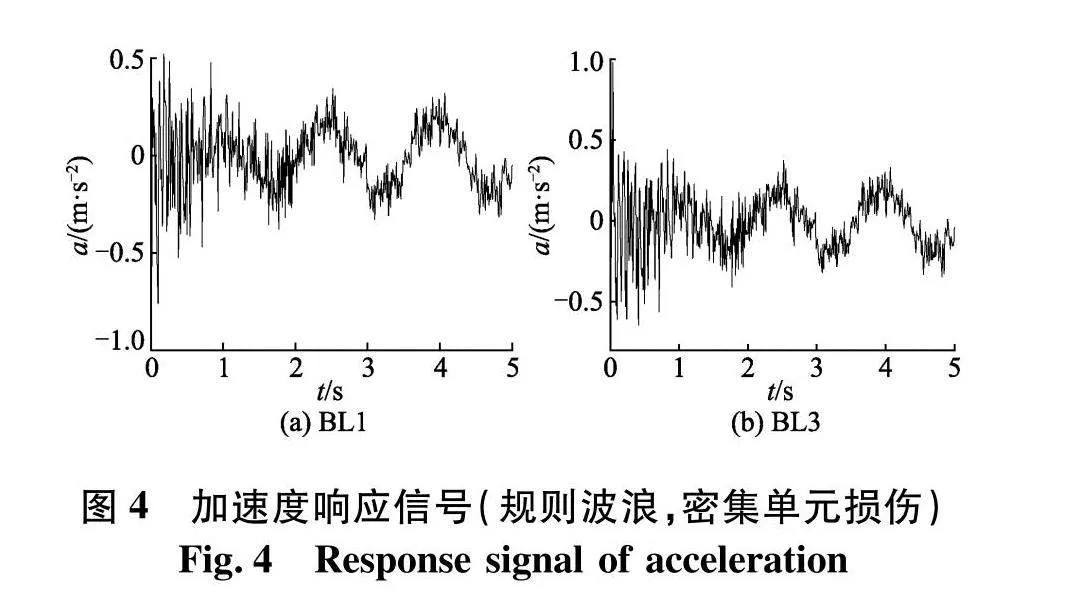
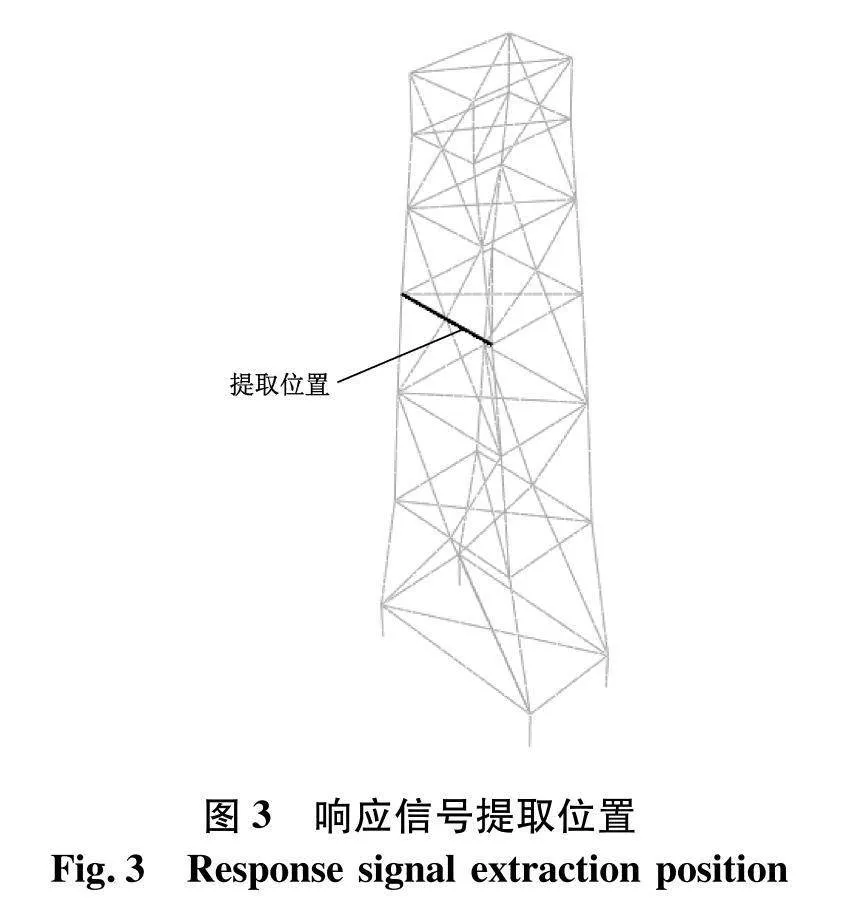
提取各工况(图3)杆件上各节点的加速度响应信号,图4给出了工况BL1和BL3节点10的前5 s加速度a响应信号,节点10在无损伤和损伤工况的响应信号在整体变化趋势上没有太大的区别,节点的加速度响应信号大致呈现出周期性的变化.
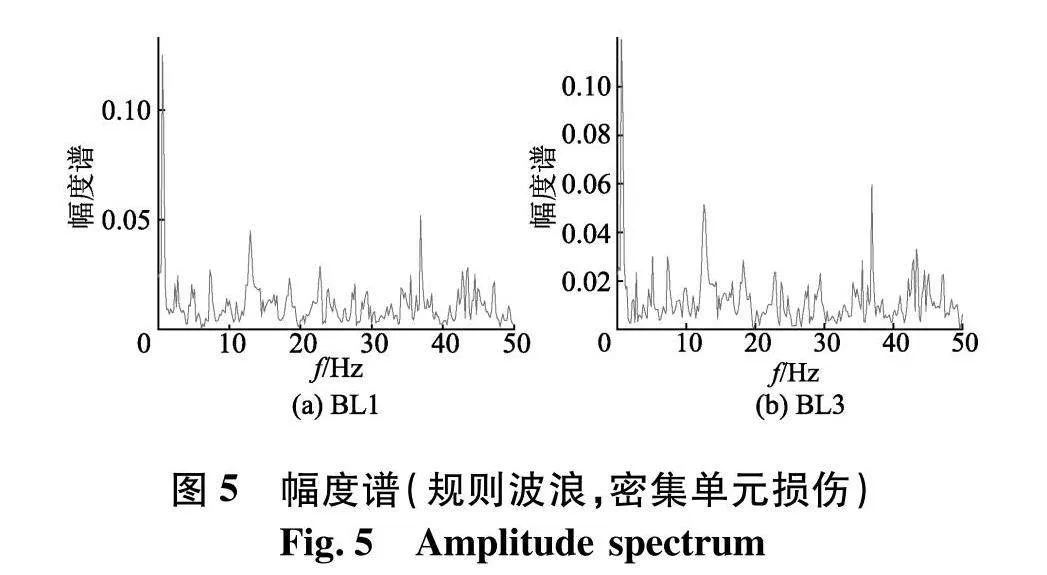
对提取的各节点加速度响应信号做傅里叶变换,得到幅度谱(图5),通过观察幅度谱从而判断分量信号的个数.从正常和损伤工况的幅度谱可以看出两者的频率成分基本一致,峰值区间也基本相同,无法直接区分正常结构和损伤结构的差别.
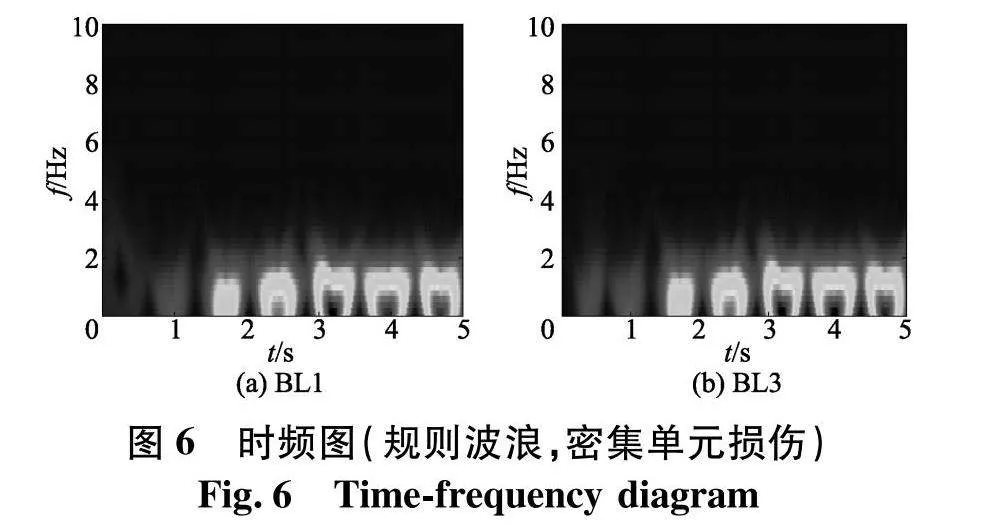
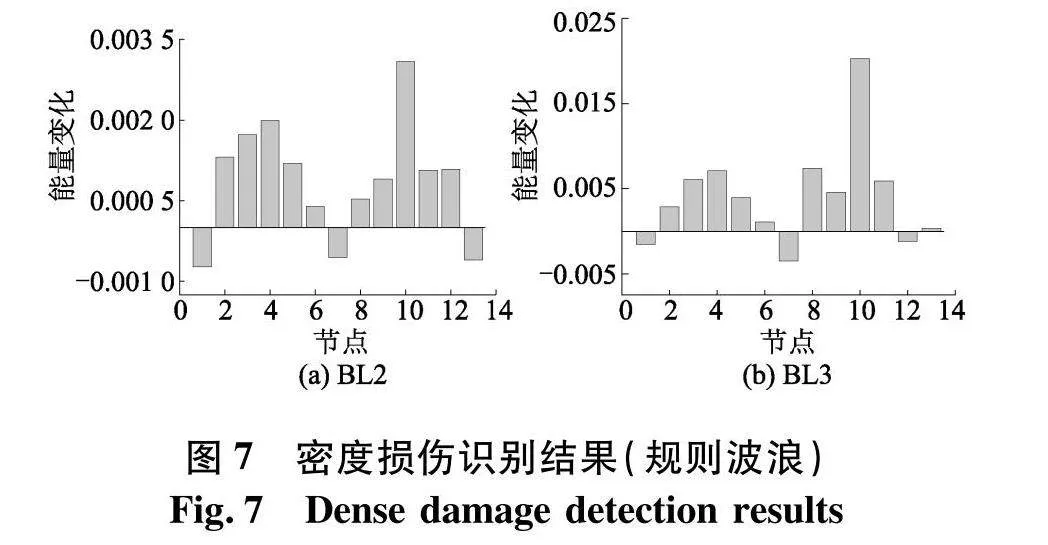
图5为幅度谱确定分量信号,对提取的各节点加速度响应信号做VMD分解,再对分量信号做Chirplet变换,得到时频图(图6),从IMF1时频图可以看出其能量主要聚集在0~10 Hz,这与幅度谱的峰值相对应,将IMF1的时频图按照公式计算能量,最后根据式(20)分别得出各个工况的能量变换(图7).
由图7可知,峰值出现在节点10(单元9和单元10的共同节点),表明在该节点处,管件此处位置受到了损伤,这与表2中预先设定的工况吻合.
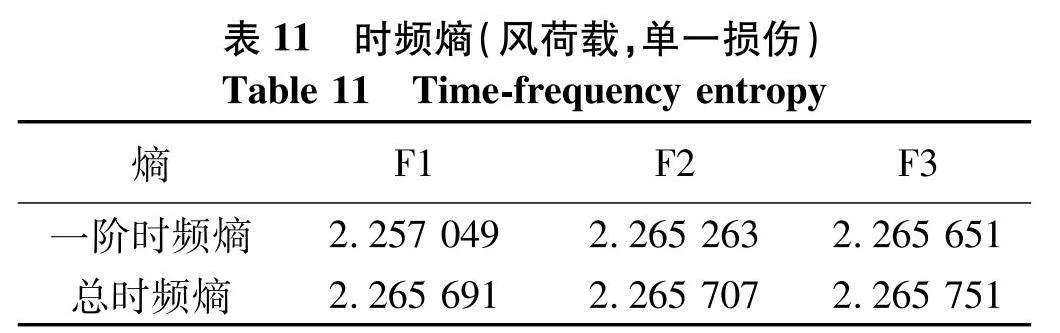
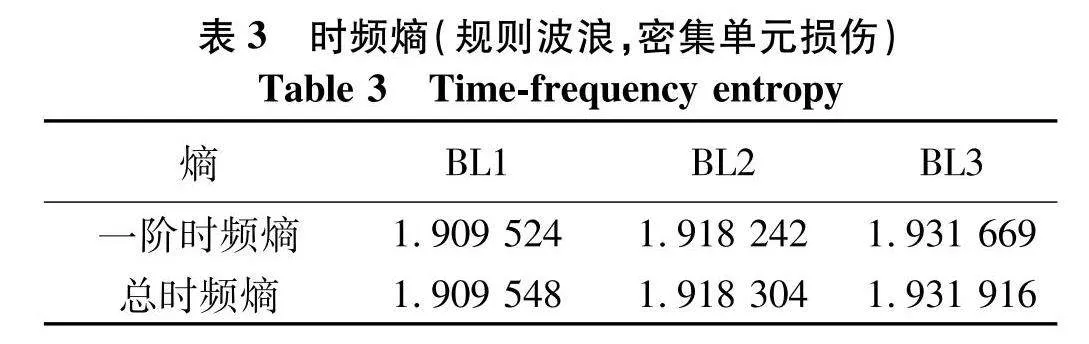
将IMF1的时频图分成若干个大小相等的区域,求出正常信号与损伤信号的时频熵值如表3,从表中可以看出,随着损伤程度的增加,时频熵逐渐增加,IMF1时频熵和总时频熵值递增,数值变化小是因为损伤部位较小,吸收的能量也相对较少,但是从整体趋势中,可以看出随着损伤的程度加剧,熵值也在增加,因此可以从熵值得变换趋势判断损伤是否在持续发展.
3.1.2 单一单元损伤识别
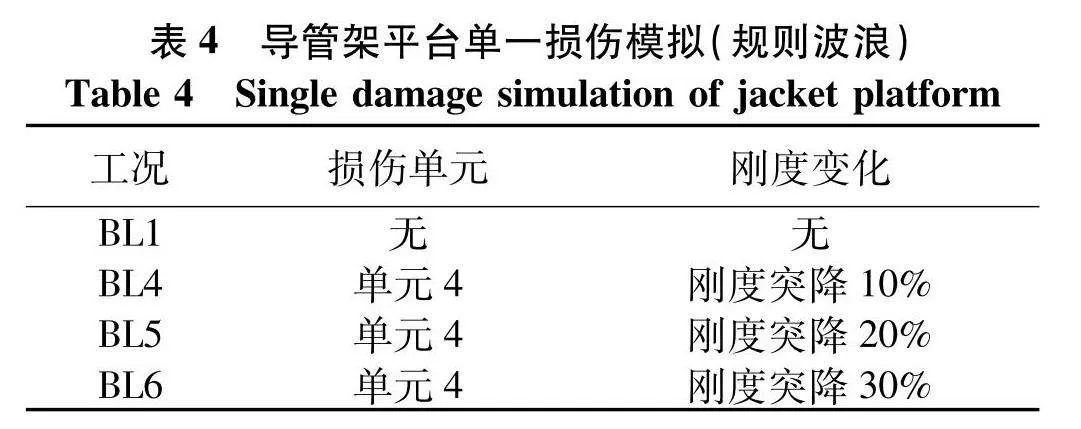
为了判断规则波浪荷载下所提方法是否能判断管件单一单元损伤位置及损伤程度,工况设置如表4.
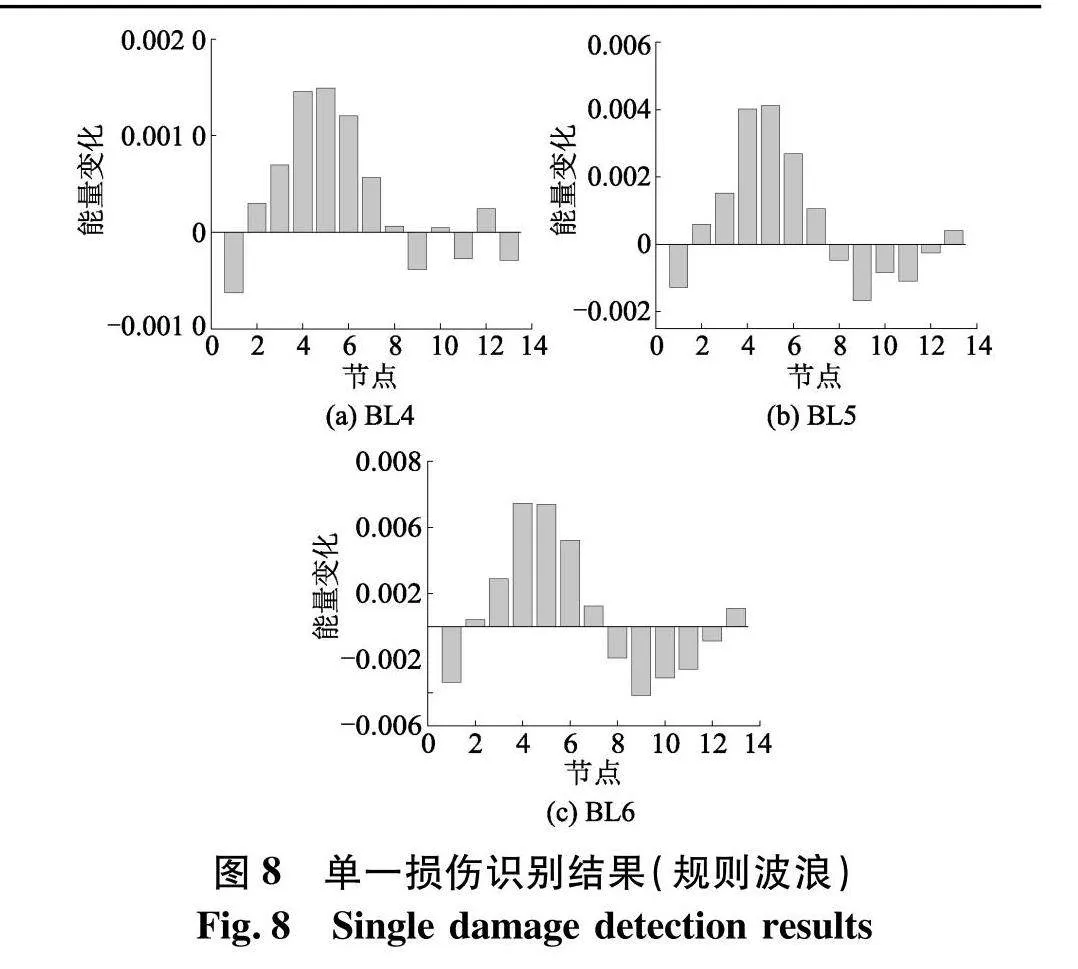
由图8可以看出能量变化在节点4、5出现较大的变化,可以判断着两个节点出现了损伤,节点4、5正好是4号单元的两个节点,与表4设置的工况相吻合.
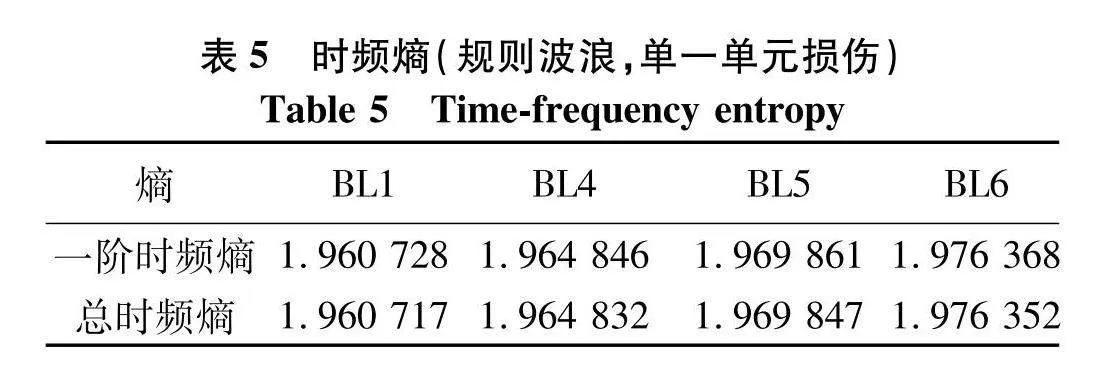
由表5可知,时频熵值随着损伤程度的增加,时频熵值在增加,表明在波浪荷载下,所提方法能判断管件单一单元损伤的位置以及损伤的程度.
3.2 不规则波浪荷载下损伤识别
3.2.1 单一单元损伤识别
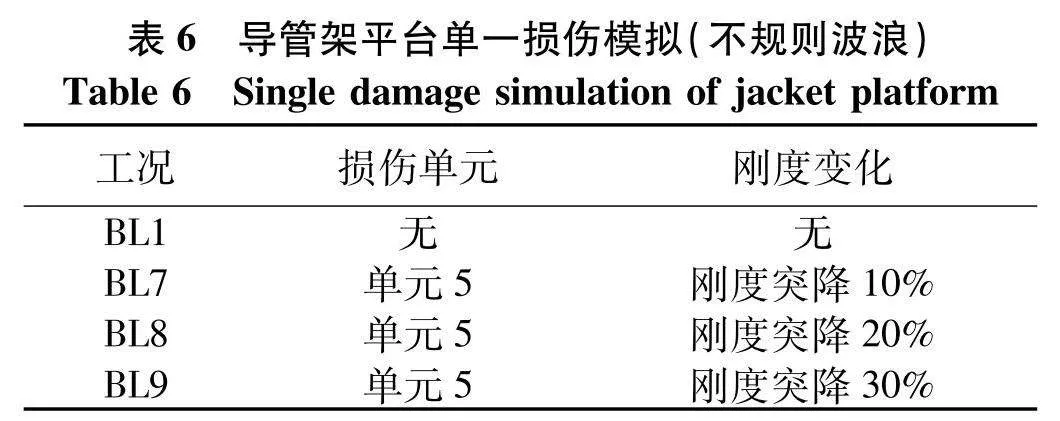
采用ABAQUS/AQUA添加Stokes不规则波,参数设置为拖拽力系数CD=1.2,惯性力系数CM=2.附加质量系数取0.5,工况设置如表6.
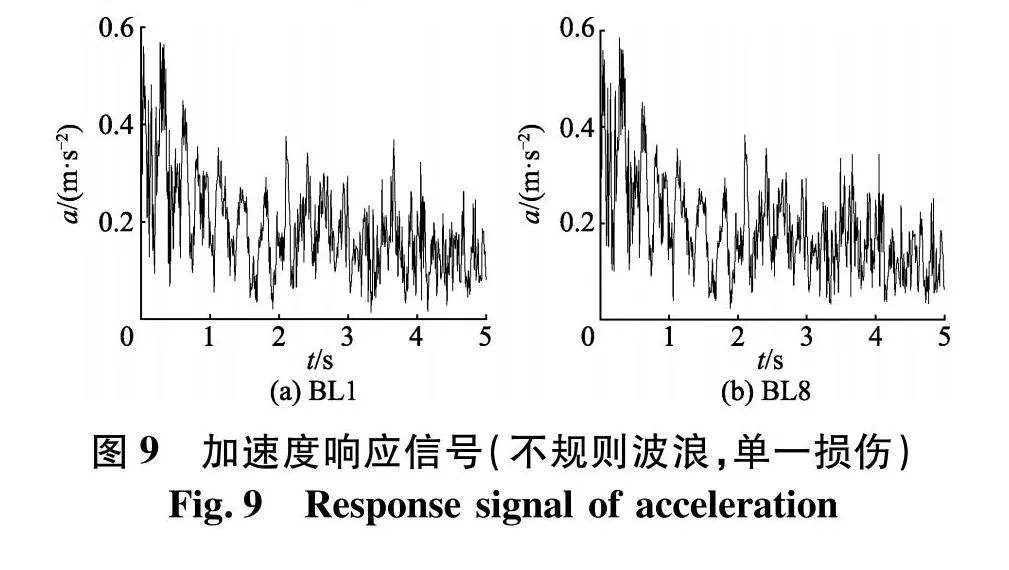
图9为加速度响应信号,可以看出在不规则波浪荷载作用下,未损伤的导管架平台节点的加速度响应信号与损伤后的加速度响应信号没有太大的区别,节点的响应信号呈现出不规则变化.
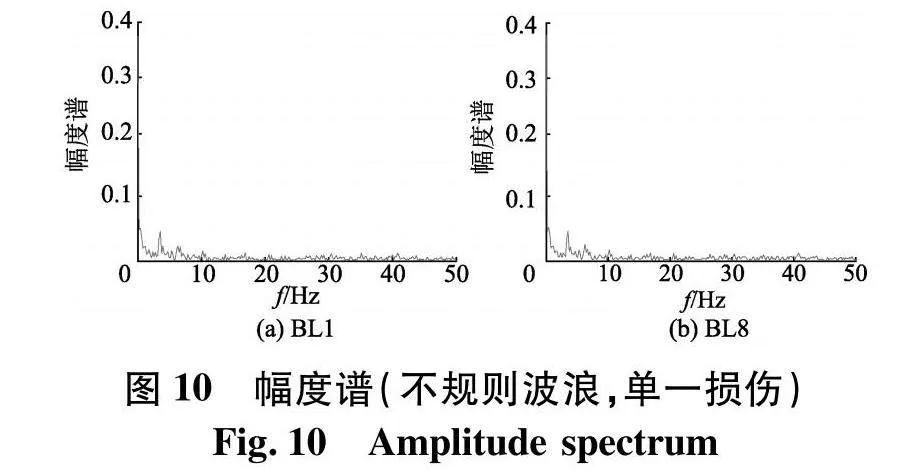
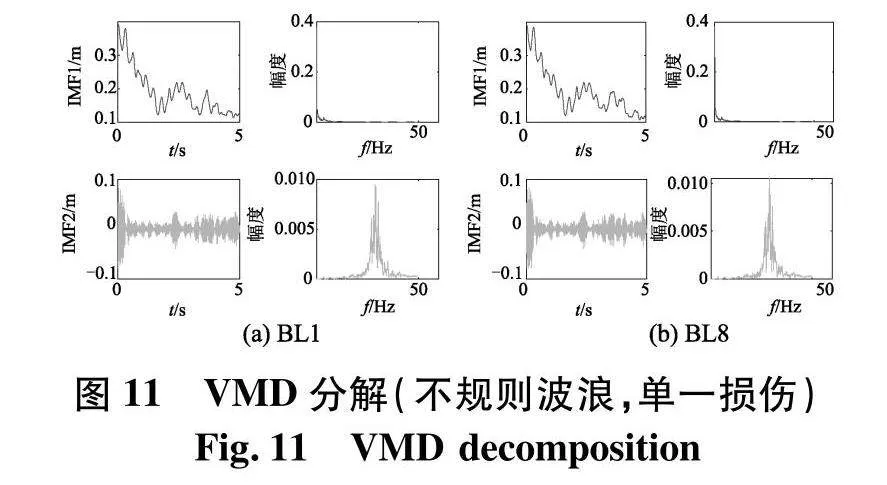
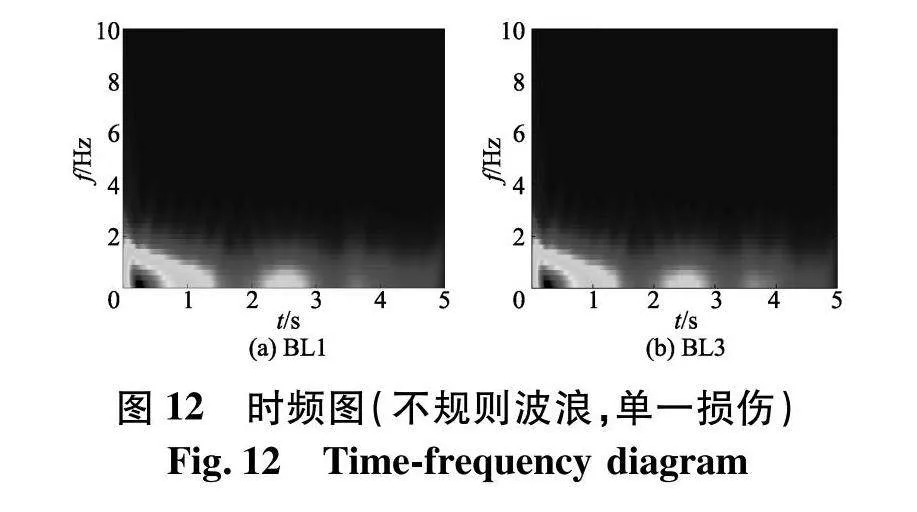
从图10可以看出,在不规则波浪荷载作用下,幅度谱峰值较为突出,峰值能量主要聚集在0~5 Hz.采用VMD对响应信号做二阶分解,分解出的模态分量如图11,IMF1的时频图如图12.
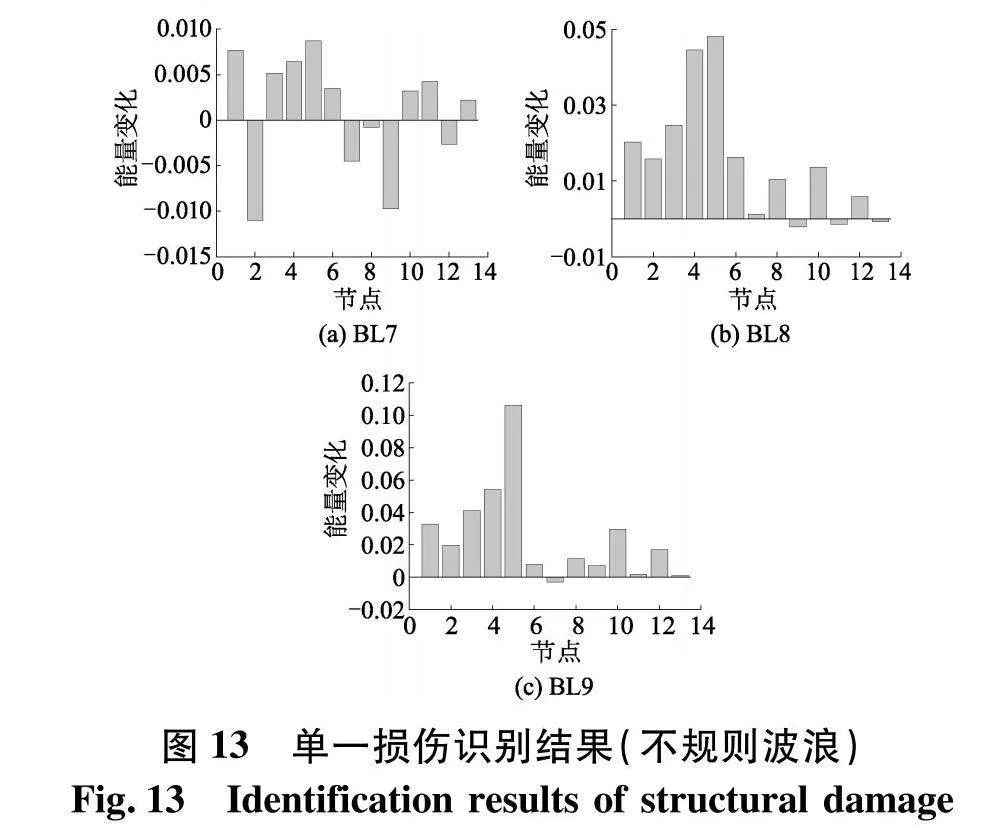
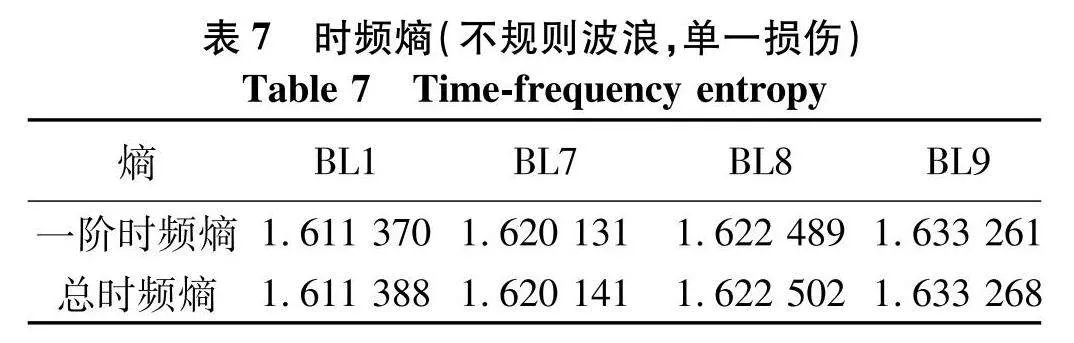
将IMF1的时频图采用式(20)计算能量变换,得到的计算结果(图13),在5号节点出现峰值,表明5号节点发生了损伤,计算结果与表6所设工况相同,能够采用文中所提的方法判断在不规则波浪荷载条件下导管架的微小损伤.将图12的IMF1时频图,分成若干个面积相等的块,采用式(21)计算IMF1的时频熵值,计算结果如表7,随着损伤程度的增加,时频熵逐渐增大.
3.2.2 分散单元损伤识别
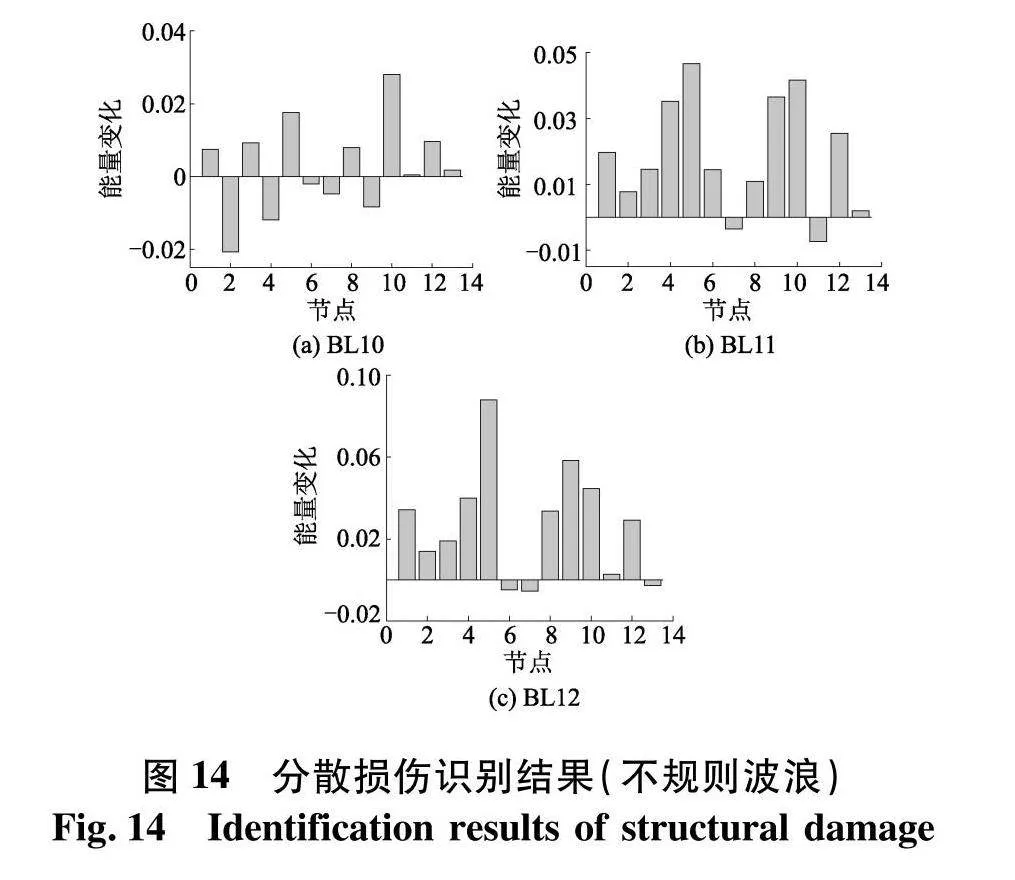
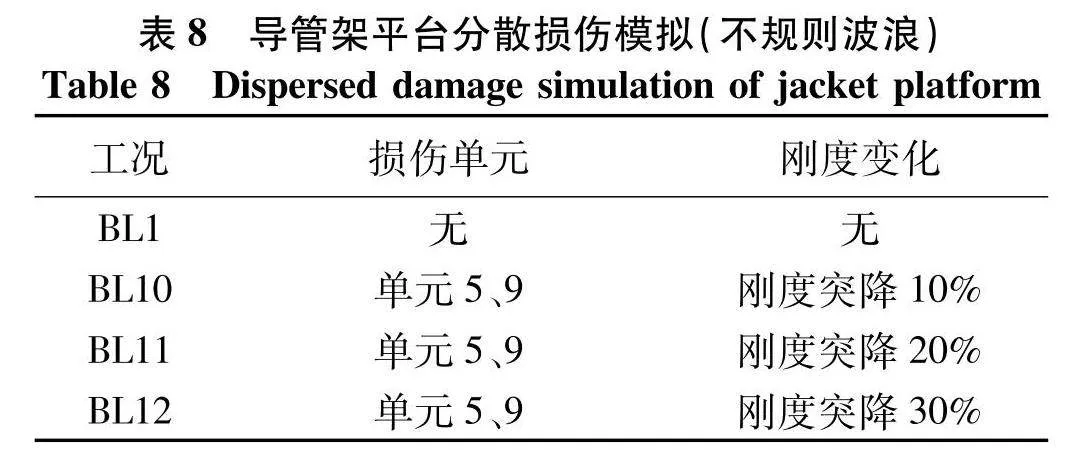
在不规则波浪荷载下,导管架结构通常会出现多处损伤,为了判断所提方法能否在不规则波浪荷载下识别多点损伤位置,工况设置如表8.
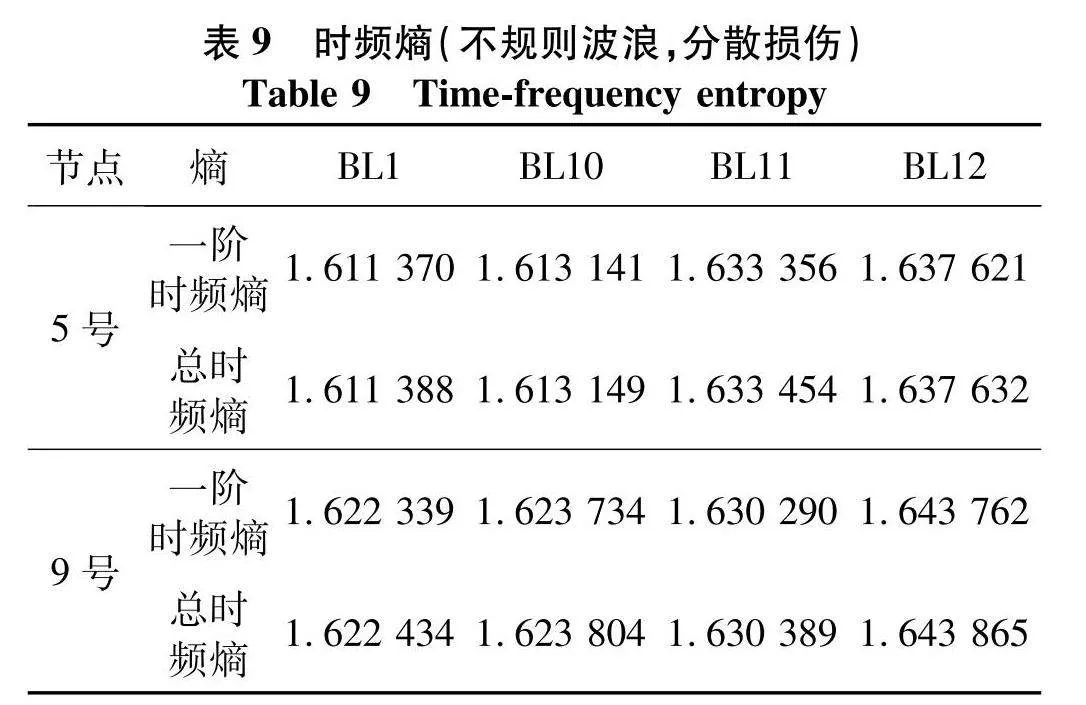
将IMF1的时频图按式(20)计算能量变换,结果如图14,在5号节点和9号节点出现峰值,表明5号节点和9号节点发生了损伤,这与表8所设工况相同,能够采用所提方法判断在不规则波浪荷载下导管架结构发生多点损伤,时频熵见表9,随着损伤程度的增加,时频熵值逐渐增大.
3.3 风荷载下损伤识别
采用Abaqus进行风荷载下导管架结构的响应计算,其中风荷载按美国API规范给出.空气密度设置为1.29 kg/m3,风速参考高度为20 m,设置风速为X方向,风速为30 m/s,Y方向上的风速为0,风速与X轴正方向的余弦值取1,风速与Y轴正方向的余弦值取0,地面粗糙系数一般取0.1~0.2,文中地面粗糙系数取0.14,结构形状拖曳系数取1.2,结构速度因数默认为1.
3.3.1 单一单元损伤识别
为了验证文中所提方法的可行性,进行风荷载作用下导管架产生单一单元损伤时的识别,工况设置如表10.
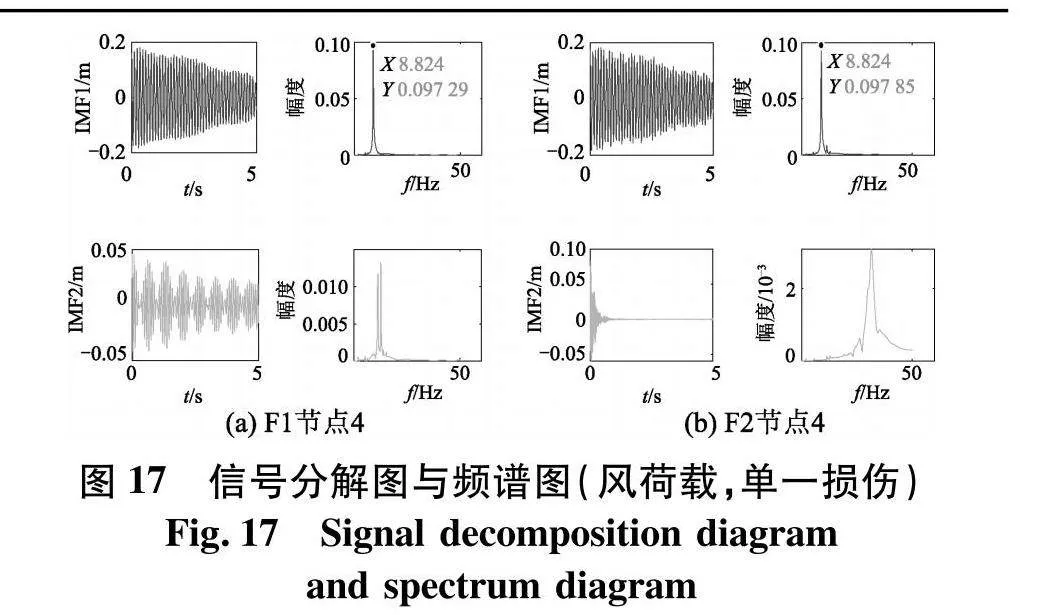
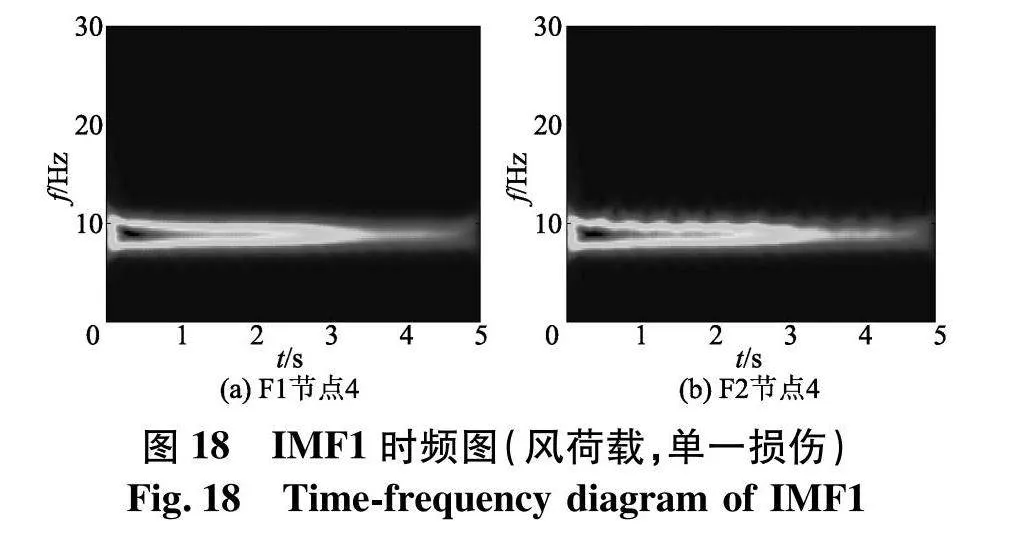
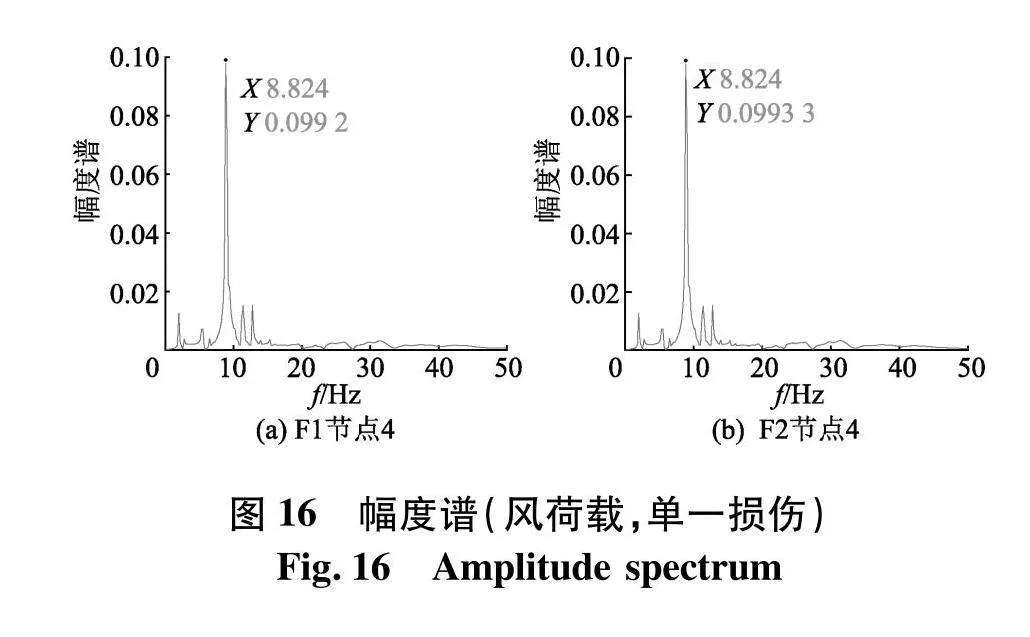
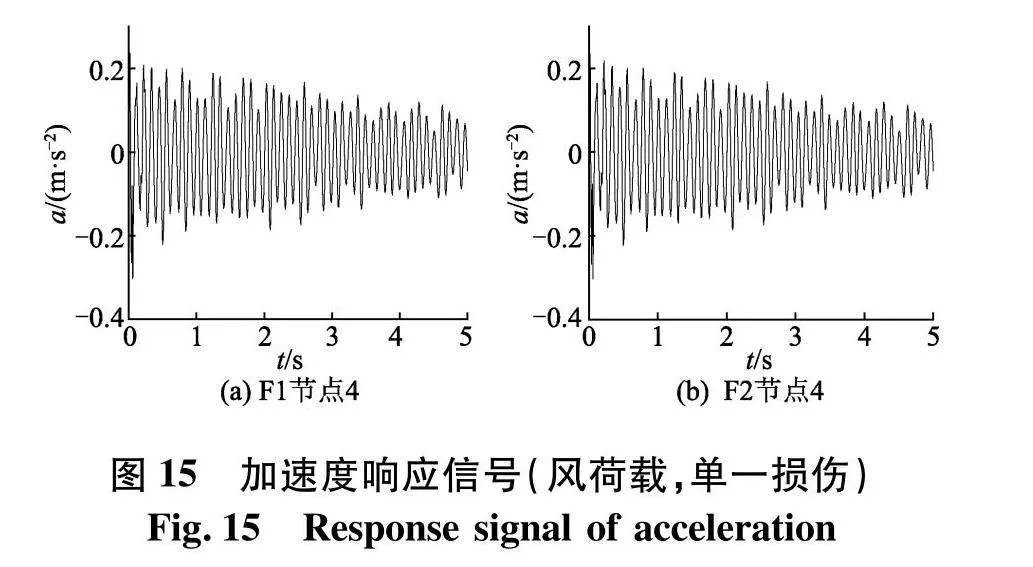
由图15~17可知,损伤前后节点4的加速度响应信号,无太大区别,无法根据响应信号判断是否损伤.采用VMD对响应信号做分解,再采用Chirplet变换对分解的信号做时频分析,得到的时频图(图18),由时频图可以观察出,能量主要聚集在10 Hz左右,说明该时频图为主分量信号时频图.
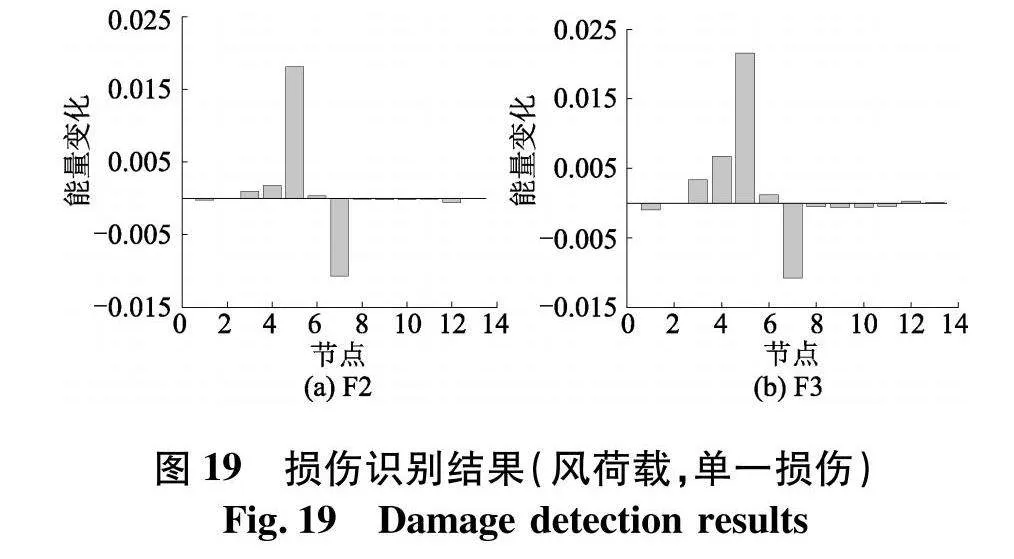
采用所述方法计算得到能量变化柱状图(图19),可以看出F1、F2和F3在节点5发生了最为明显的能量突变,可以判断单元4发生了损伤.根据图18计算损伤前后的时频熵,将其分成100块大小相等的区域块,按式(21)计算时频熵,随着损伤程度的增加,时频熵逐渐增加.
3.3.2 密集单元损伤识别
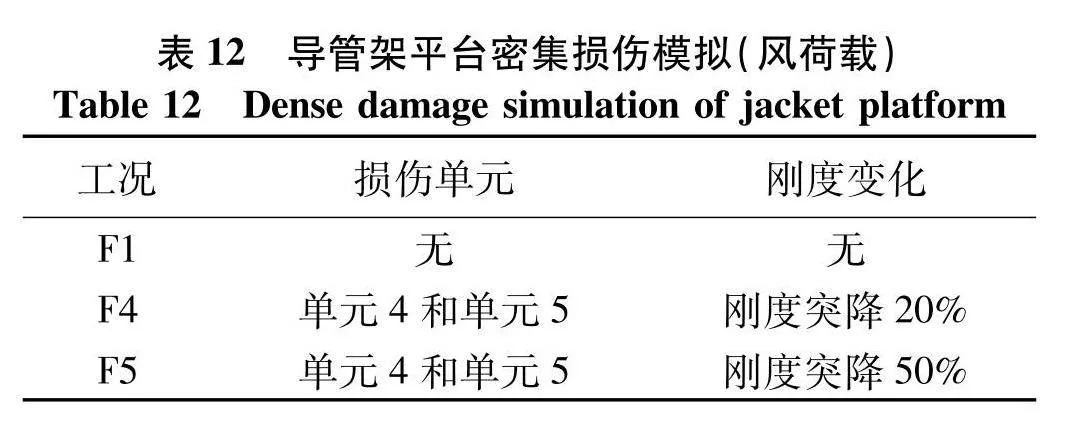
为了检验导管架结构在风荷载条件下密集损伤产生的情况,工况设置如表12.
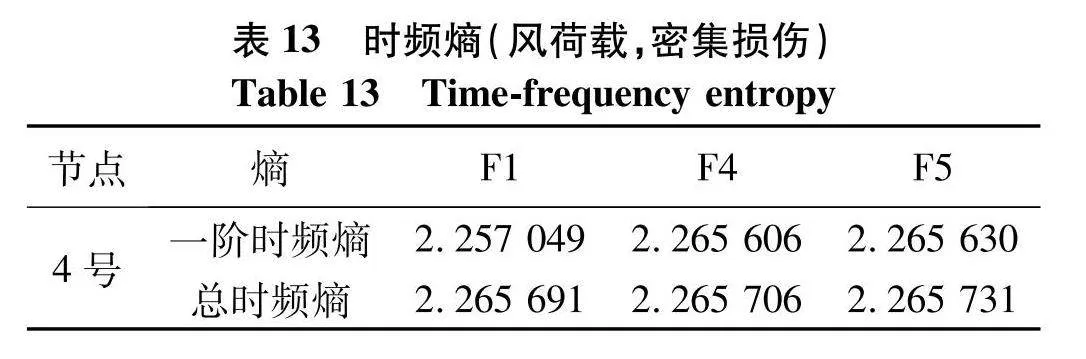
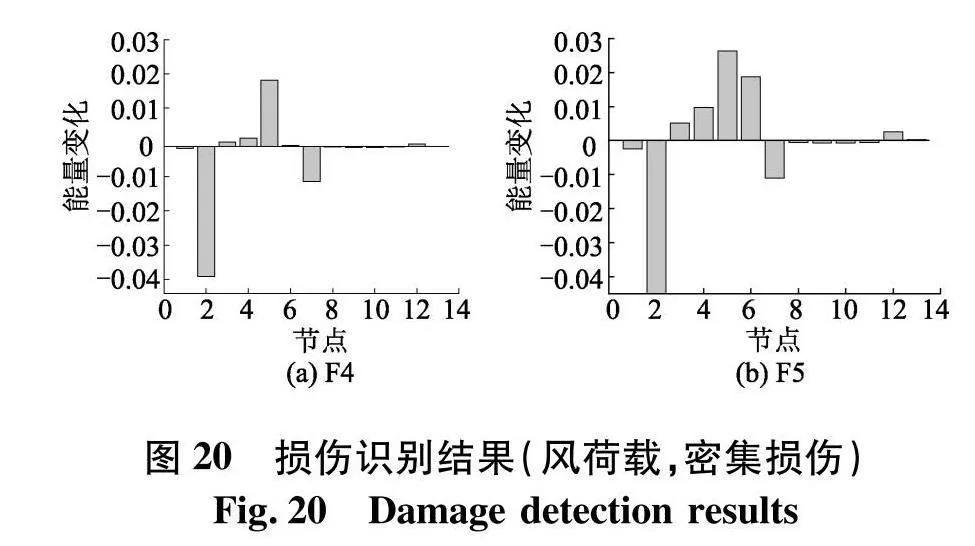
能量计算结果如图20,5号节点能量变化最大且为正值,与表12所设定的工况相同,表明可以识别损伤位置,时频熵见表13,由表可知随着损伤程度的增加,时频熵逐渐增大.
4 结论
(1) 结构工程响应一般为多分量信号,利用VMD可以有效减少模态混叠及端点效应,极大提高时频能量的聚集性,识别的时频曲线更加清晰.
(2) 计算结果表明,所提方法能够有效地识别导管架结构在不同环境荷载复杂工况下的单点损伤和多点损伤,具有较好的稳定性和较广的适用性.
参考文献(References)
[1] 嵇春艳, 陈明璐. 基于小波变换与神经网络的海洋平台结构损伤识别与定位研究 [J]. 海洋技术, 2009, 28(4): 113-116.
[2] 刁延松, 张启亮, 孟冬梅. 基于振动传递率的钢质导管架海洋平台结构损伤识别方法研究 [J]. 建筑钢结构进展, 2013, 15(1): 50-56.
[3] 林星文. 导管架平台损伤特性及损伤识别方法研究 [D]. 上海:上海交通大学, 2017.
[4] HE J H, LIU D P, CHUNG C H, et al. Identification of multiple local damage to an offshore jacket substructure using a novel strain expansion-reduction approach [J]. Applied Sciences, 2020,10:7791-7802.
[5] WANG S, XU M. Modal strain energy-based structural damage identification: A review and comparative study [J]. Structural Engineering International, 2018, 29(2): 234-248.
[6] MOHANTY S, GUPTA K K, RAJU K S. Hurst based vibro-acoustic feature extraction of bearing using EMD and VMD[J]. Measurement,2018,117:200-220.
[7] 彭威. 波浪荷载作用下导管架平台TLD减振研究 [D]. 南京:南京航空航天大学, 2019.
[8] 那鑫宇. 非线性波浪作用下的弧形防浪墙响应研究 [D]. 武汉:武汉理工大学, 2020.
[9] American Petroleum Institute. API recommended practice for planning, designing and constructing fixed offshore Platforms [M]. US:American Petroleum Institute," 1974.
[10] 曾昭发 ,吴丰收, 黄玲, 等. 自适应Chirplet变换及其在探地雷达目标探测中的应用[J]. Applied Geophysics,2009, 6(2): 192-200,203.
[11] 杨芳, 高静怀. Chirplet变换中的参数选择研究[J]. 西安交通大学学报, 2006,40(6): 719-723.
[12] 王胜春, 韩捷, 李志农, 等. 一种自适应Chirplet分解方法及在故障诊断中应用[J]. 振动工程学报, 2007,20(6): 606-612.
[13] 刘景良, 任伟新, 王佐才, 等. 基于同步挤压小波变换的结构瞬时频率识别[J]. 振动与冲击, 2013, 32(18): 37-42,48.
[14] 王思帆. 基于小波能量的梁结构损伤位置及时变损伤识别[D]. 福州:福建农林大学, 2019.
[15] 时培明, 张慧超, 韩东颖. 基于改进自适应多元变分模态分解的轴承故障诊断方法研究[J]. 动力工程学报, 2022, 42(2): 129-137.
[16] GABOR D. Theory of communication: The analysis of information [J]. Journal of the Institution of Electrical Engineers-part III: Radio and Communication Engineering, 1946, 93(26): 429-441.
[17] 孙宁, 秦洪懋. 基于Winger谱时频熵在齿轮故障诊断中的应用 [J]. 制造业自动化,2015,37(3):60-62.
(责任编辑:贡洪殿)
