风浪流联合作用下单桩式风机与三脚架式风机动力响应对比研究
2024-01-11王春波陈实齐博崔锟郭玉晗张玉


摘 要: 风机选型是风场设计的重要内容,需从经济性和安全性两个方面进行考虑,其中安全性主要分析风机结构在风、浪、流等外部环境荷载作用下的极限承载力和疲劳寿命,而风机结构响应是以上分析的基础内容.文中以美国国家可再生能源实验室(national renewable energy laboratory,NREL)5 MW风机为研究目标,建立了单桩式和三脚架式两种不同类型海上固定式风机模型,选取北太平洋海域海况,将风、浪、流与风机结构进行全耦合仿真,得到单桩式和三脚架式两种不同形式的风机运动响应,对比分析了风机叶片、塔筒和基础处的位移和载荷,可见三脚架式风机总体性能优于单桩式风机,为北太平洋海域的固定式风机选型提供了技术依据.
关键词: 耦合;固定式风机;单桩基础;三脚架基础;动力响应
中图分类号:TK83"" 文献标志码:A"""" 文章编号:1673-4807(2024)06-007-07
收稿日期: 2023-06-22"" 修回日期: 2021-04-29
基金项目: 优秀青年科学基金项目(52222111)
作者简介: 王春波(1982—),男,高级工程师,研究方向为海上风机结构.E-mail:wangchb14@cnooc.com.cn
*通信作者: 张玉(1983—),女,博士,教授,研究方向为海洋结构与装备设计、分析.E-mail:zhangyu@cup.edu.cn
引文格式: 王春波,陈实,齐博,等.风浪流联合作用下单桩式风机与三脚架式风机动力响应对比研究[J].江苏科技大学学报(自然科学版),2024,38(6):7-13.DOI:10.20061/j.issn.1673-4807.2024.06.002.
Comparative study on the dynamic response of monopile type windturbines and tripod type wind turbines under the combined effectof wind and wave currents
WANG Chunbo1,CHEN Shi1,QI Bo1,CUI Kun2,GUO Yuhan3,ZHANG" Yu3*
(1.Clean Energy Branch,CNOOC Energy Technology amp; Services Limited, Tianjin 300459, China)
(2.Offshore Petroleum Engineering Co.Ltd.,Qingdao 266500, China)
(3.College of Safety and Ocean Engineering, China University of Petroleum,Beijing 102249, China)
Abstract:The wind turbine selection is an important part of the wind farm design, which needs to be considered from both economic and safety aspects, among which safety mainly analyzes the ultimate bearing capacity and fatigue life of the wind turbine structure under the action of external environmental loads such as wind, waves and currents, and the structural response of the wind turbine is the basis of the above analysis. In this paper, the 5 MW wind turbine of NREL(national renewable energy laboratory) is used as the research target, and two different types of offshore fixed wind turbine models, monopile type and tripod type, are established, and the sea conditions of the North Pacific Ocean are selected, and the wind, waves and currents are fully coupled with the wind turbine structure for simulation, and the wind turbine motion response of monopile type and tripod type are obtained. The overall performance of the tripod type wind turbine is better than that of the monopile type wind turbine. This study provides a technical basis for the selection of fixed wind turbines.
Key words:coupling,stationary wind turbine,monopile foundation,tripod foundation,dynamic response
海上风能具有清洁无公害等特点,并且其来源稳定,无需复杂的探索开采流程,因此海上风能具备大规模开发利用的前景[1].海上风机作为利用海上风能的主要设备,可以按照支撑结构分为固定式风机和浮式风机,固定式基础主要适用于10~60 m海域,主要基础类型有单桩式基础、三脚架式基础、重力式基础、三桩基础、扭式导管架基础等.大于60 m的海域主要是漂浮式风机,包括驳船式风机、半潜式平台风机、张力腿式风机等.由于长时间在海洋中进行工作,需承受风、浪、流等诸多随机荷载联合作用,所以对承载能力和动态性能要求更高.倘若不综合考虑各种环境荷载因素对风机结构的影响,一旦发生意外,将导致重大经济损失[2].
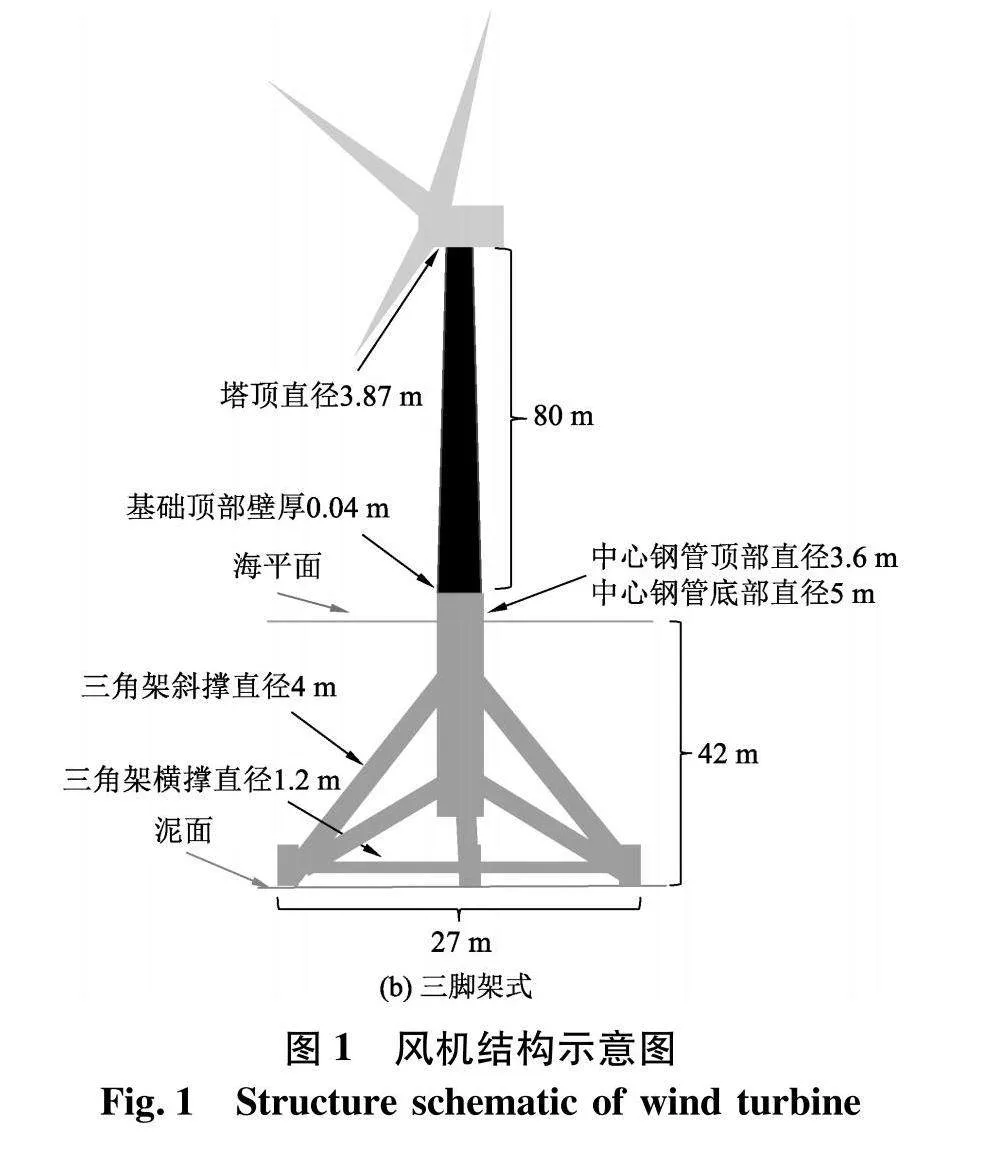
单桩式风机适用的水深一般为10~30 m的近海海域中,安装时不需要对海床进行整理,但是随着海流对海床的冲刷有可能会使埋地部分过多暴露在海水中,进而导致风机整体稳定性下降,所以在进行打桩安装时,目标海域的海床位置和基岩层距离不能过远,这样基岩层可以有效抵抗整个风机结构的倾覆力,可以提供更好的稳定性和基础强度[3].三脚架式风机适用的水深一般在20~50 m的海域中,三脚架基础是由不同直径和壁厚的圆柱钢管连接组成,中心钢管作为主要支撑与斜撑和横撑以及其余钢桩共同组成了三脚架式风机基础,当上部风电机组受到荷载时,下部的支撑钢管会将载荷分散,增强了总体结构的刚度和强度.三脚架是风机基础在安装时,基础的水平度控制需配有浮坞等海上固定平台完成,由于其需要在底部三角形三个角的位置上分别打桩,所以其不适用于海床存在大面积岩石的海域.
在应用方面,单桩基础动态性能较好,基础形式简单[4],水线面积较小并且没有复杂的复合结构,根据欧洲风能协会的统计数据,单桩式基础在近海风机应用中占到75%.而海上风速会随着离海岸线的距离的增加而不断增大,所以三脚架基础所适用的海域风速较大,风资源较好德国的Alpha Ventus风电场已安装12台5 MW的三脚架海上风机,英国也于2020年在东安格利亚地区的海上风电场安装102台7 MW三脚导管架式海上风机基础,我国在如东潮间带风电场有2.5 MW三脚架海上风机试验机组[5].未来三脚架式风机也很有可能成为近海固定式风机的主流机型.
单桩式风机和三脚架固定式风机被普遍应用在浅海地区,而对结构简单成本较低的单桩式风机与稳定性较好的三脚架式风机的动态性能研究也是重中之重.文献[6]使用LS-DYNA对海上风电机组单桩基础和三脚架基础遭遇船舶撞击时的响应做出了研究,结果显示在遭遇撞击时,三脚架基础机舱响应值低于单桩基础约32%,动态响应明显比单桩基础小,稳定性较高.文献[7]计算了单桩式风机塔架在风浪以及地震作用下的动力响应,进一步验证了环境载荷之间是一种相互作用和影响的耦合关系,在对风机进行计算时,不可以忽视环境载荷之间的耦合影响.文献[8]采用COMSOL软件对台风工况下的单桩基础风机和导管架基础风机动态响应进行了对比分析,结果显示在台风天气中,导管架基础的优势远远大于单桩基础.为了比较准确的预测在不同环境工况下海上风机支撑系统的动态响应情况[9],在Abaqus中成功建立起了单桩式风机支撑系统预测变形的概率模型,对海上风机支撑结构的安全运行有重大意义.文中基于GH Bladed软件,以美国国家可再生能源实验室(national renewable energy laboratory,NREL) 5 MW风机为研究对象,建立了海上单桩式风机和三脚架式风机两种风机模型,选取了北太平洋海域环境工况作为风机工作海况,对该海况产生的风、浪、流对风机的作用进行了耦合分析,最终对所得到的风机动态响应的结果以及风机的综合性能进行了对比.
1 风机结构模型分析
1.1 风机几何结构
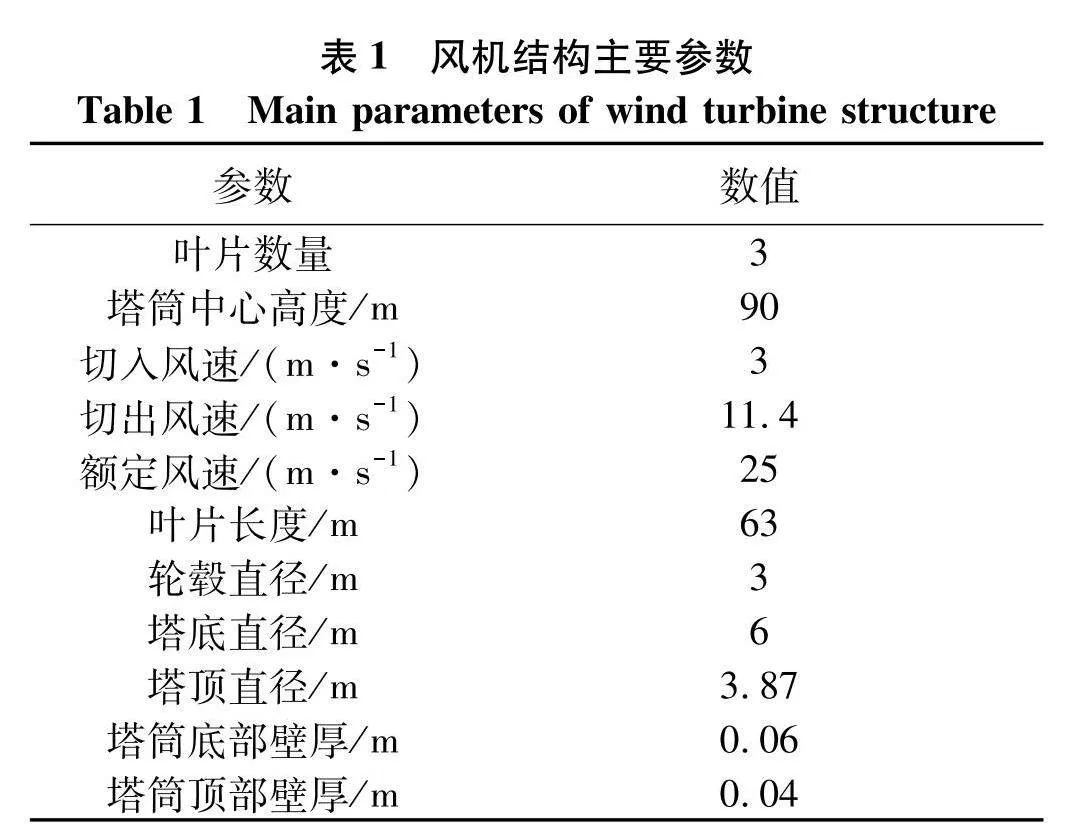
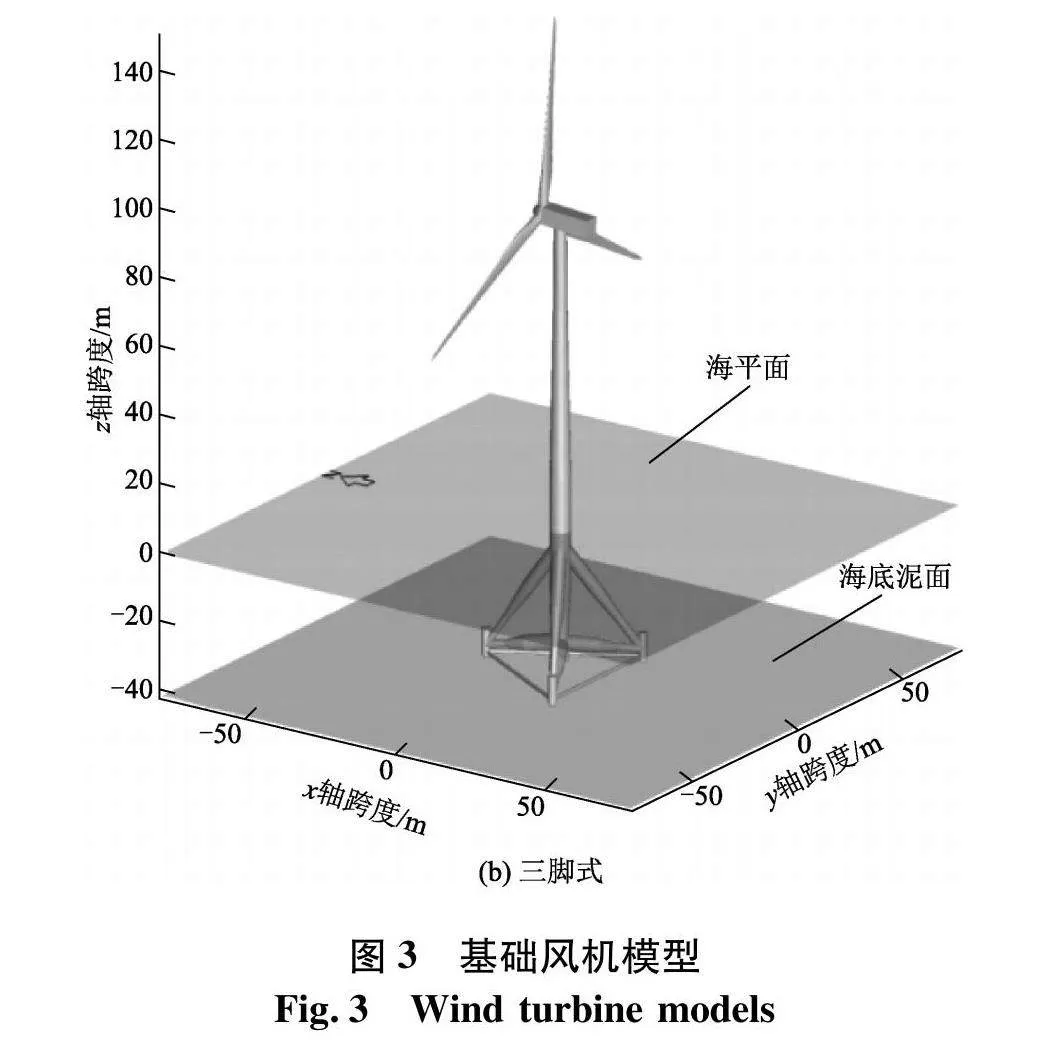
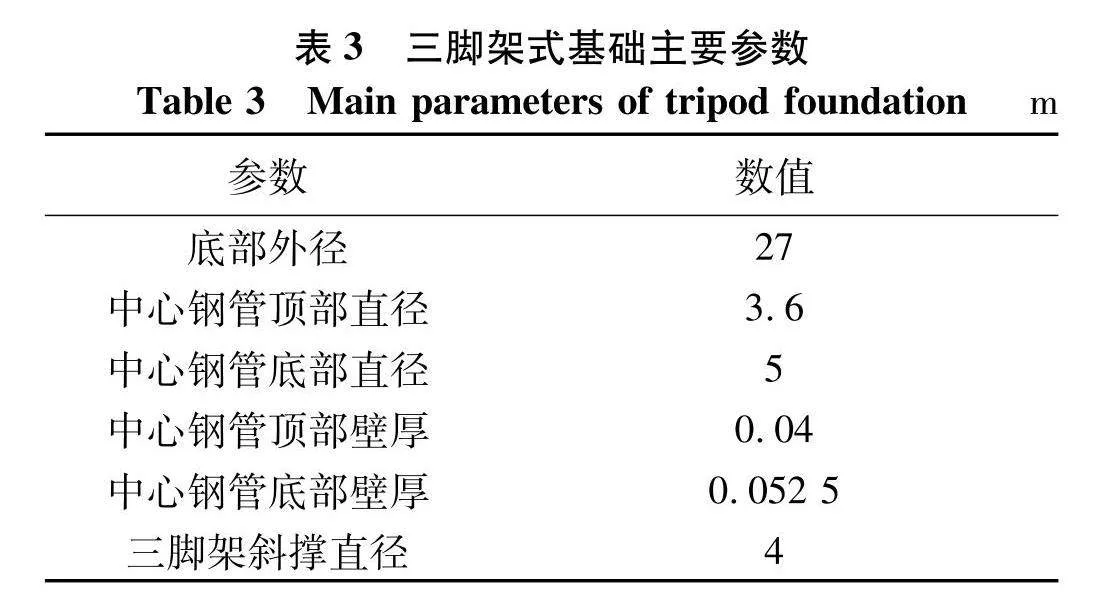
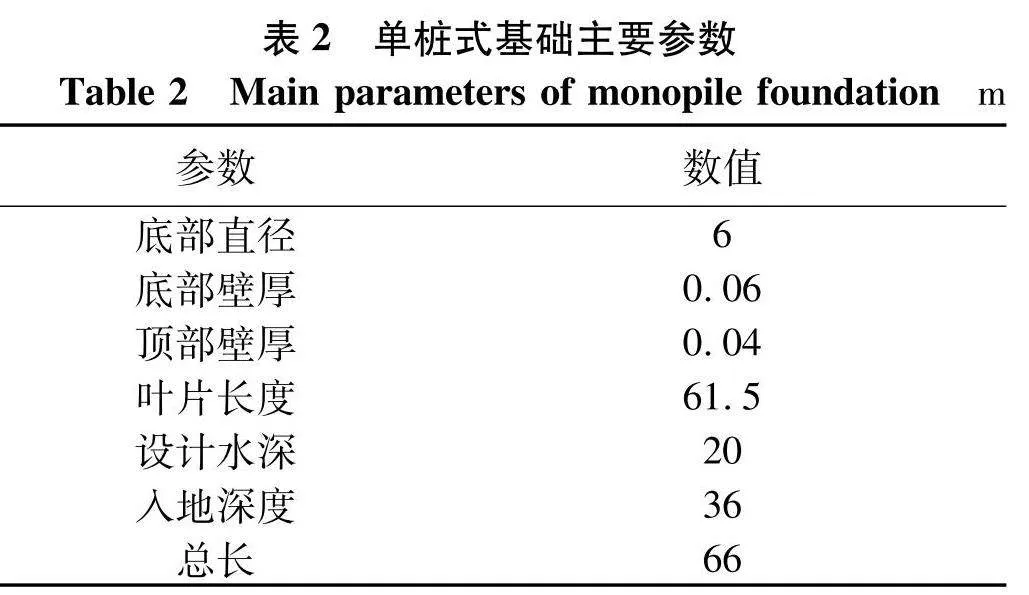
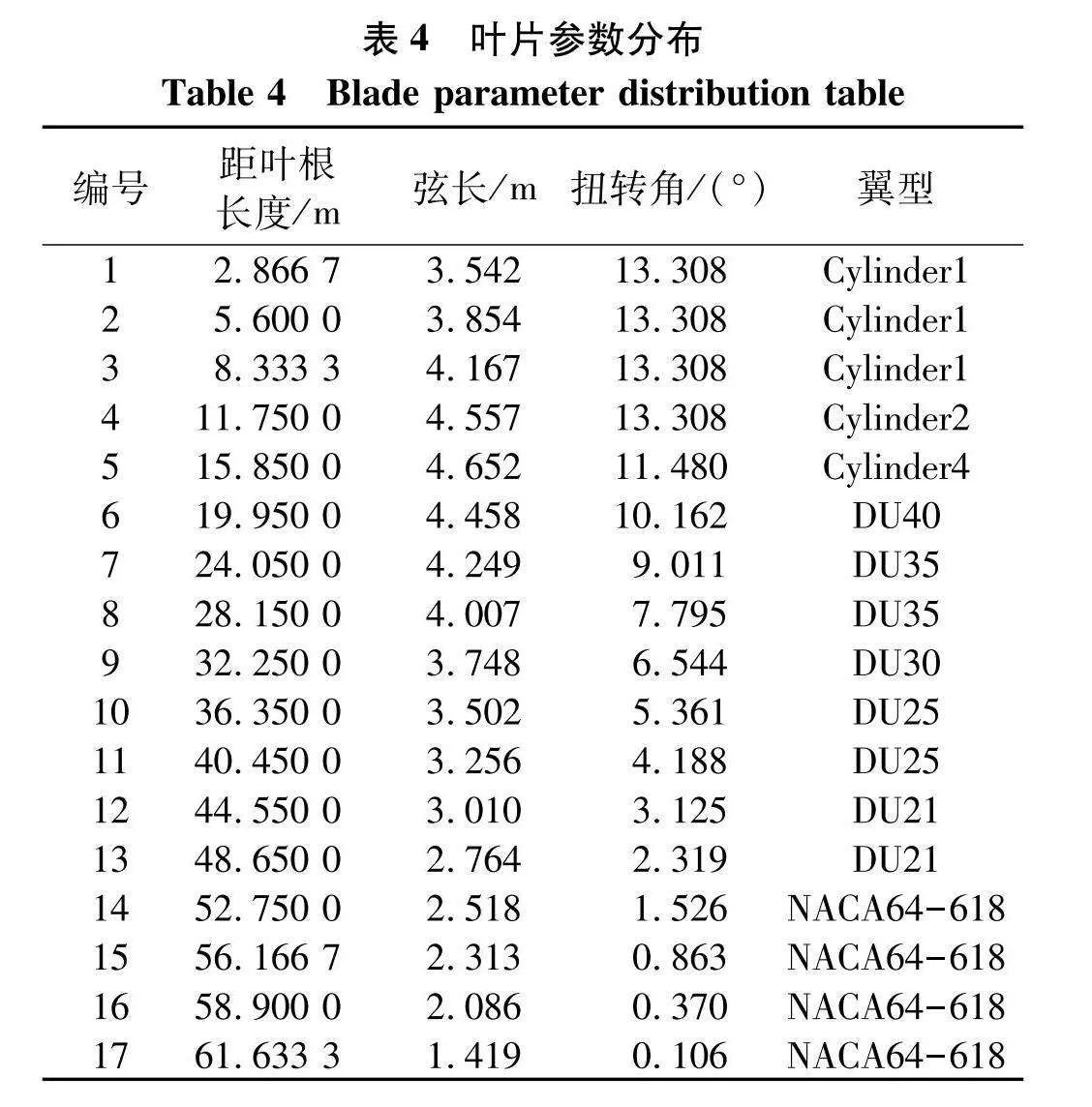
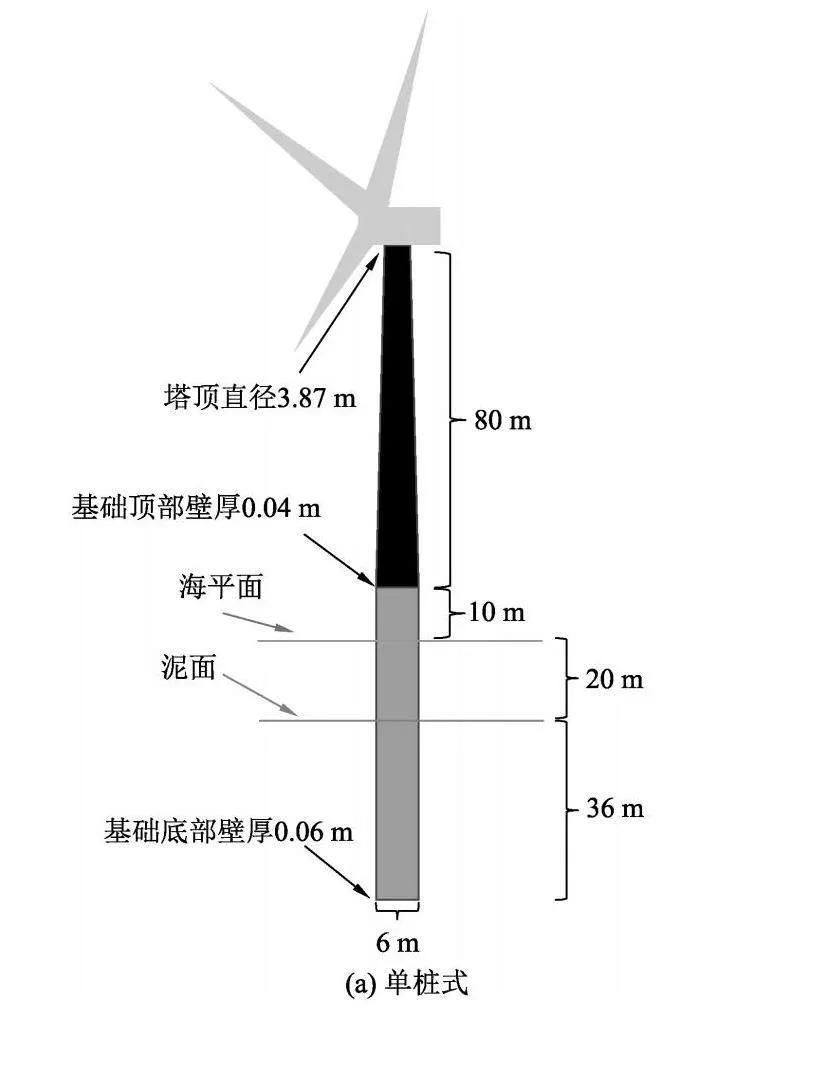
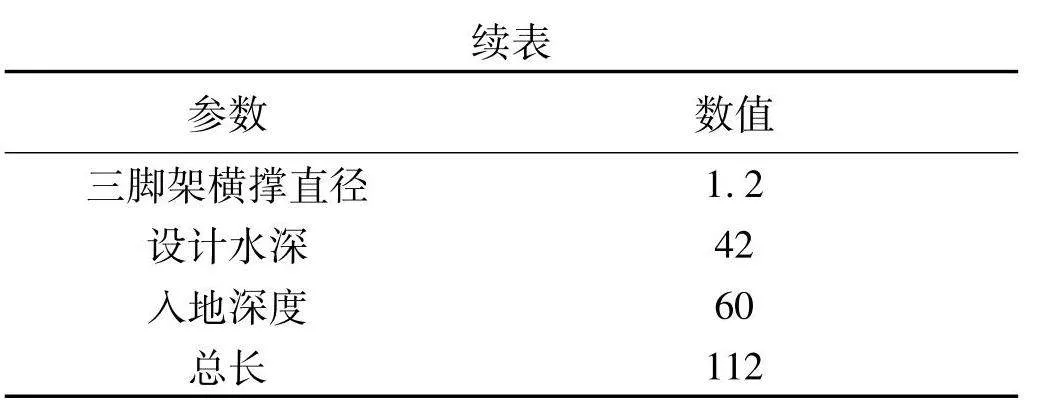
以NREL 5 MW风机为研究目标,风机主要结构如图1,参数如表1,基础类型分别为单桩式和三脚架式,塔筒和基础分别选用了8 500和7 850 kg·m-1的钢材,所选取得单桩基础的主要参数如表2,三脚架式基础结构参数如表3,叶片主要参数如表4,三维图如图2[10].
最终在GH Bladed中建立的单桩式风机和三脚架固定式风机的模型如图3.
1.2 载荷计算
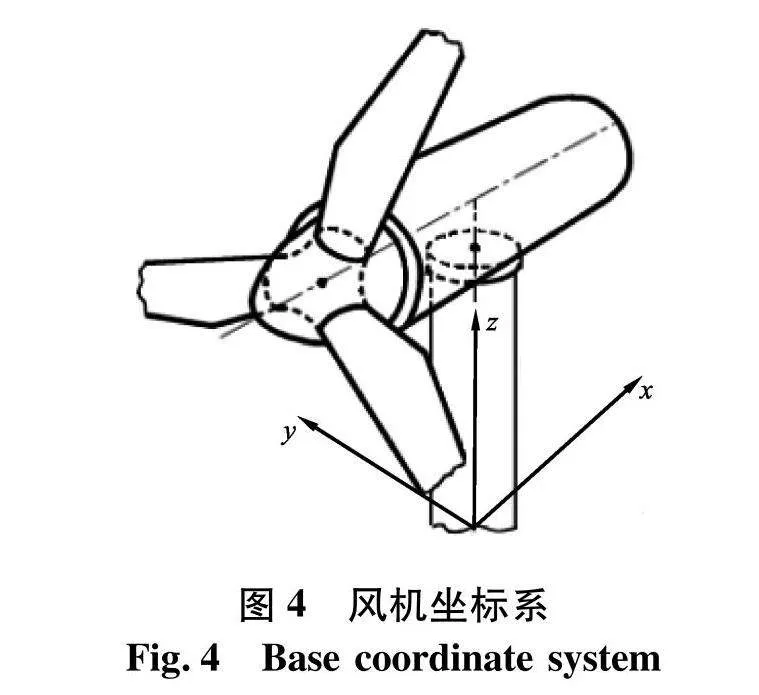
对风机进行计算时选用的坐标系如图4.
风速模型一般分为定常风和湍流风,所产生的空气动力荷载主要作用在位于海平面以上的风机结构.定常风属于风荷载的长谱峰周期部分,其周期大大超过了结构自身的自振周期,因此可以将定常风视为静荷载.湍流风是典型的随机过程,属于短周期荷载,有可能使得结构产生共振,其动力特性一般不可忽略.选用的湍流风谱的Kaimal风谱,其谱密度表达式为[11]:
Su(ω)=σ2u4L/Vhub(1+6ωL/Vhub)5/3(1)
式中:Su(ω)为湍流风速谱密度;ω为频率;Vhub为轮毂高度处的平均风速; L为湍流尺度参数;σu为湍流风速均方根值.
文中进行叶轮的空气动力学计算时,所用的理论为叶素动量理论,其控制方程为:
dT1=4πρv21a(1-a)rdr
dM1=4πρv1Ωb(1-a)r3dr
dT2=12ρW2(CLcos φ+CDsin φ)Ncdr
dM2=12ρW2(CLsin φ-CDsin φ)Ncrdr(2)
式中:T为推力;M为扭矩;ρ为空气密度;r为风轮半径;α为轴向诱导系数;b为切向诱导系数;Ω为风速度矢量;N为风轮叶片数;CL翼型升力系数;CD翼型阻力系数,W为风速在叶素处产生轴向速度和切向速度的矢量合;c为弦长.
支撑机构上的风荷载主要是气流流经结构产生的拖曳力,可按下式进行计算[12]:
Fwind=12CDρDvv(3)
式中:Fwind为支撑结构所受的风荷载;CD为气动拖曳力系数;ρ为空气密度;D为构件直径;v为风速.
在计算海流力时可将流体对基础结构的作用视为平面流的冲击,在风机结构上总海流力为[13]:
Fc=ρD2g∫H0CDv2dz(4)
式中:Fc为总海流力; g为重力加速度;v为海流流速;H为海流冲击高度;CD为拖曳力系数;ρ为海水密度;D为结构直径.
对于直径与波长之比小于0.2的细长桩结构的波浪荷载计算采用工程上典型的Morison方程,作用在单位长度塔筒上的波浪力表达式为[14]:
dF=ρπD24CMvdz+12ρCDDvvdz(5)
式中:F为波浪力;ρ为海水密度;D为结构直径;CM为惯性力系数;CD为拖曳力系数;v为海流流速.
1.3 海况计算
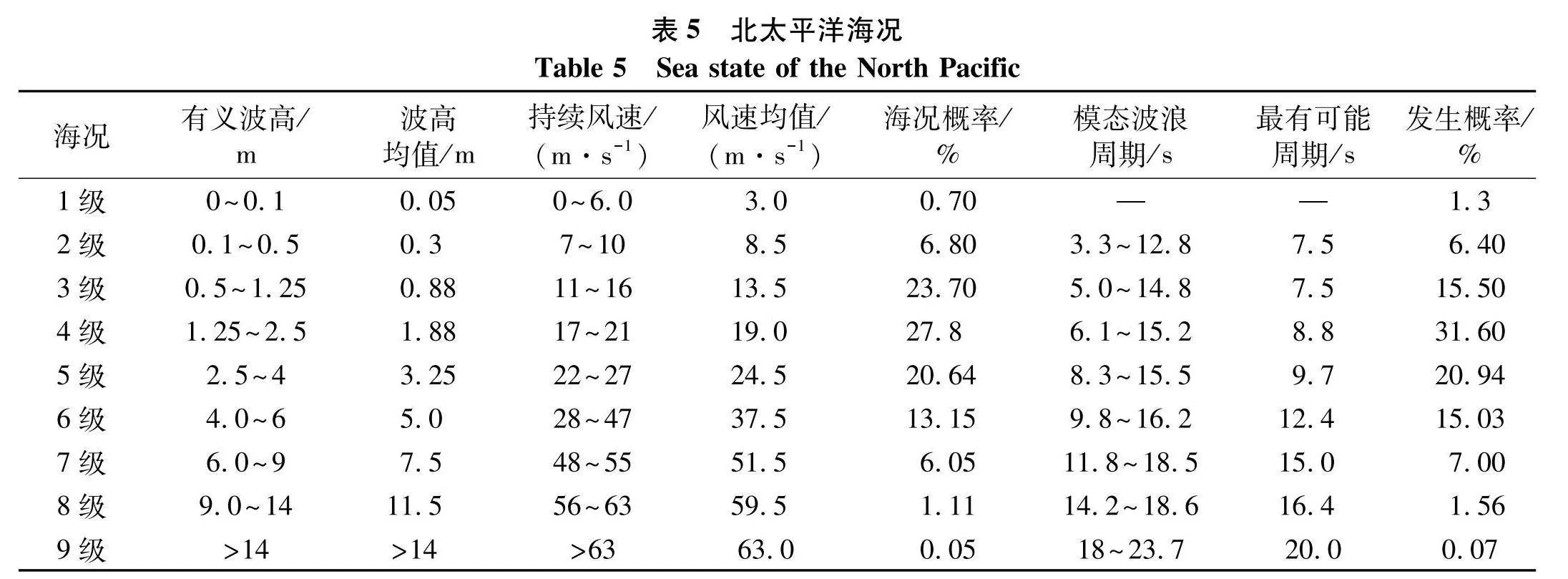
北太平洋海况由相关资料统计[15]得到,如表5.针对北太平洋多发的4级海况作为计算海况,风、浪、流的方向均为正x方向,风场使用湍流风场模型,在GH Bladed中建立风速为17~21 m·s-1的3D湍流风场,设定风场的参考高度为轮毂中心处的高度.
2 风机动态响应及对比分析
在Bladed中完成对风机整体结构的建模和工作海况的设定后,设置模拟时长为300 s,对叶片、塔筒、基础的载荷和位移进行了研究,得到了两种固定式风机在相同海况下的动态响应对比.
2.1 叶片动态响应分析
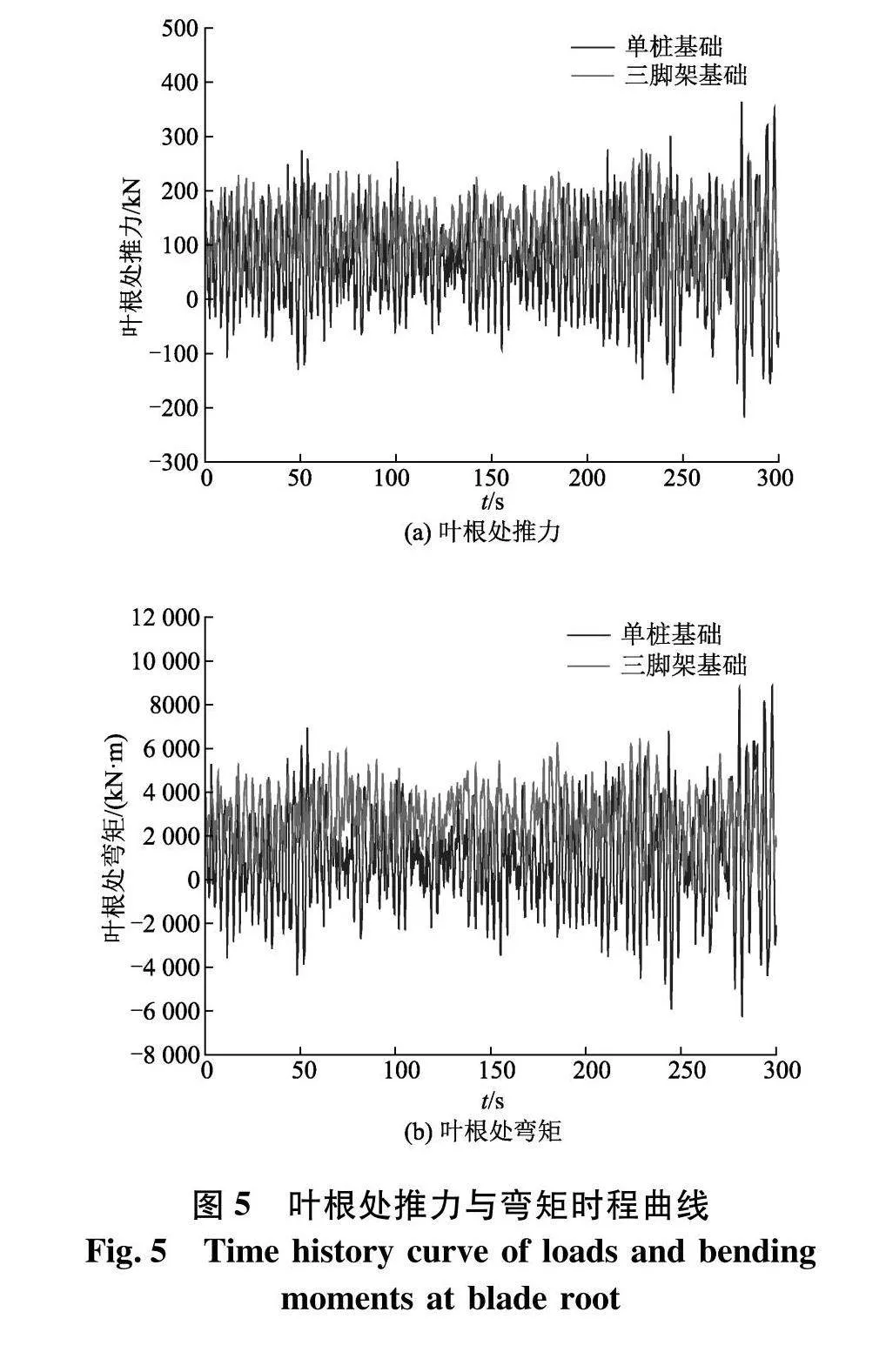
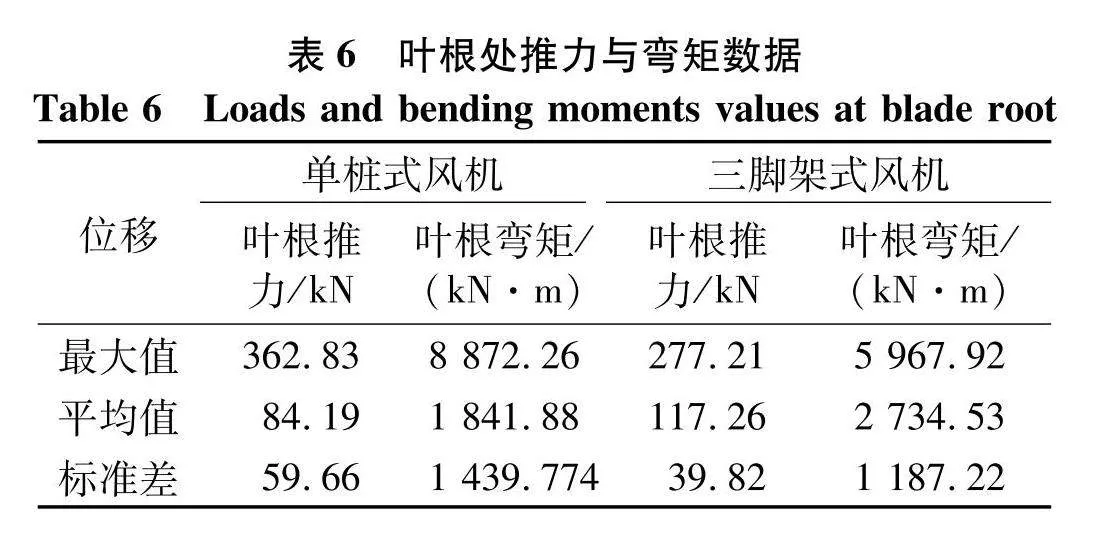
由GH Bladed软件分析可得叶根处推力最大,叶根在x方向上所受推力和y方向上的弯矩求解结果如图5,表6为叶根处推力和弯矩统计.
由表6可以得到,在相同的海况条件下,单桩式风机叶根处推力和弯矩的最大值比三脚架式风机高30.8%和48.6%,三脚架式风机叶根推力和弯矩的平均值比单桩式风机高32.97%和48.46%,但可以看出单桩式风机叶根推力和弯矩的标准差比三脚架式标准差高49.82%和21.27%,说明单桩式风机叶根处所受推力值和弯矩值浮动较大,所以单桩式风机叶片叶根处损伤或折断的几率更大.
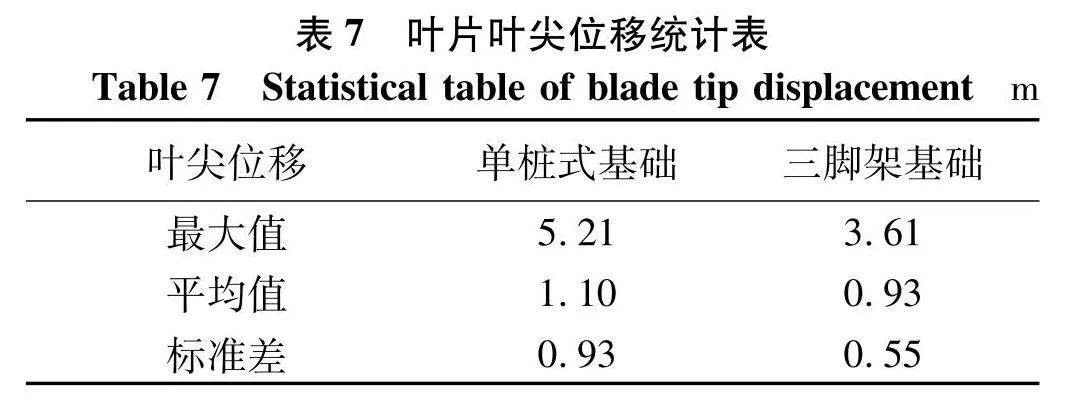
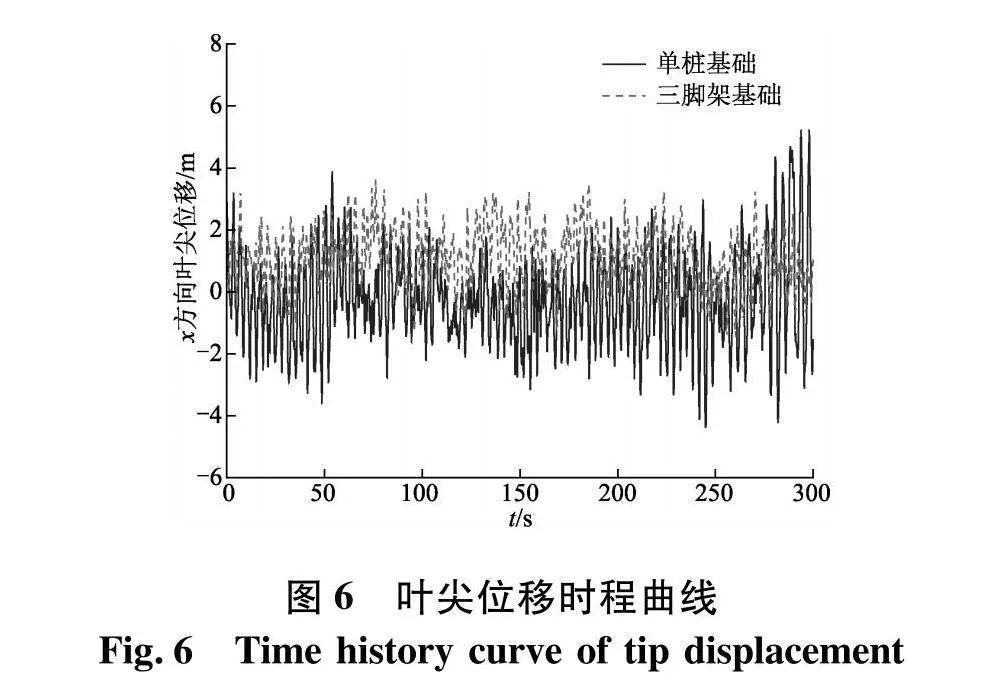
在风机叶片不同位置的位移响应中,叶尖处的位移一般为响应最大的位置,因此针对两种不同形式的风机叶尖x方向上的位移也进行了仿真分析得到结果如图6和表7.
在相同海况下,单桩式风机叶尖位移最大值比三脚架式风机高44.32%,单桩式风机叶尖位移平均值及标准差也大于三脚架式基础,单桩式风机基础风轮受风面积大,所承受的风荷载也较大,其叶片变形更加剧烈,风机整体结构稳定性较低.
2.2 塔筒及基础动态响应分析
风机塔筒越高、叶片越长,风机运转所吸收的风能就越大,这对于降低度电成本、推广风电产业的意义重大,但风机的大型化使得所受的弯矩载荷变大,在强烈风载等其他载荷的作用下,高耸柔性的塔筒会产生剧烈的摇晃摆动,对这种剧烈位移不加以控制会降低塔筒疲劳寿命增加风机倒塌的风险,因此对塔筒尤其是位移响应最大的塔顶的研究是至关重要的.
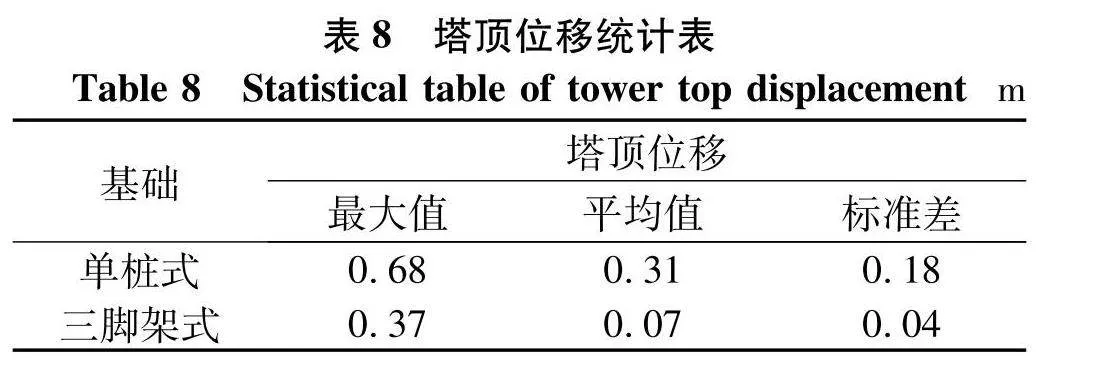
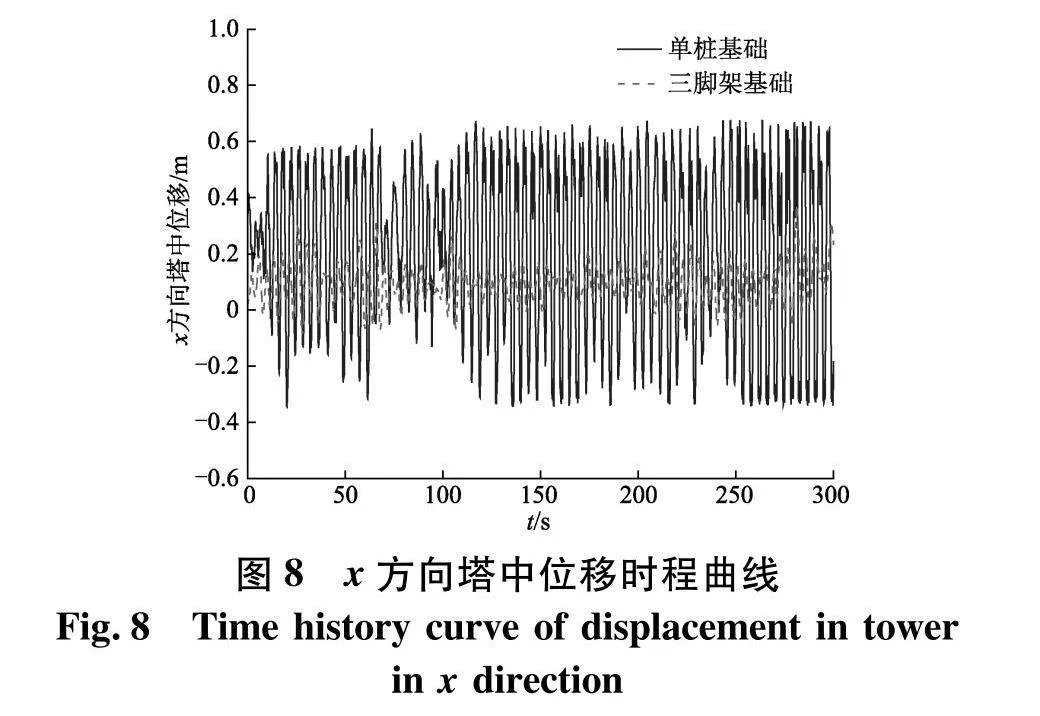
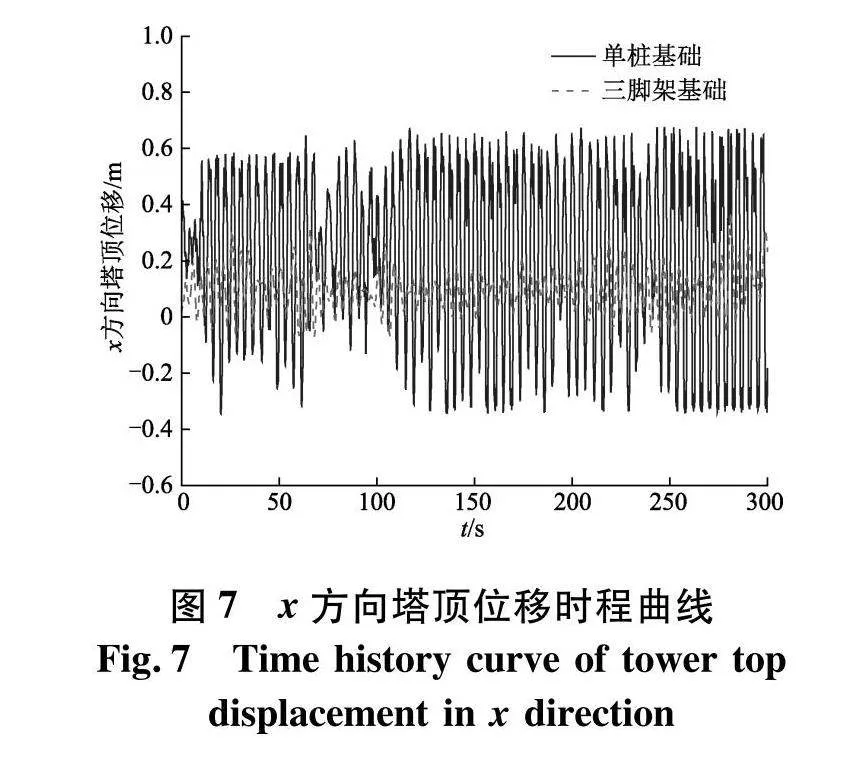
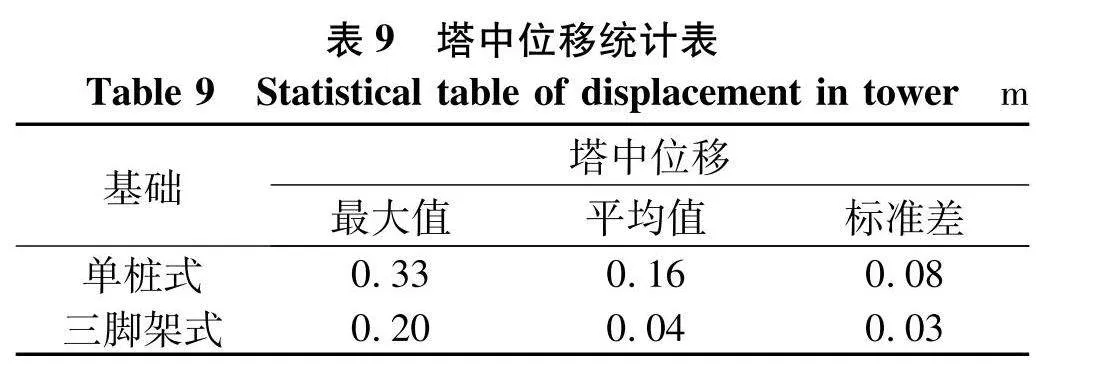
如图7、8分别为塔筒顶部和塔筒中部处水平方向位移时程曲线,塔筒顶部位移按照悬壁梁结构刚度的校核方法进行校核,塔筒顶部的位移与塔筒高度的比值应限制在0.25%~1%,单桩基础和三脚架式基础塔筒顶端位移极值分别为0.68、0.37 m,悬臂长度取塔筒在竖直方向上的尺寸 80 m,则塔顶位移极值均位于悬臂长的0.25%~1%,在要求范围内,故塔筒的塔顶位移值符合要求.
由图7、8可知,当两种类型的风机处在同一工况下时,单桩式风机相较于三脚架式风机的塔筒位移响应幅值变化较大.由表8、9可得,单桩式风机塔顶和塔中位移最大值比三脚架式风机高83.7%和65%,单桩式风机塔顶和塔中位移平均值是三脚架式风机的3.4倍和3倍,标准差也大于三脚架式风机.由此可见,当环境变量相同时,三脚架式风机塔筒部分的动态响应优于单桩式风机.
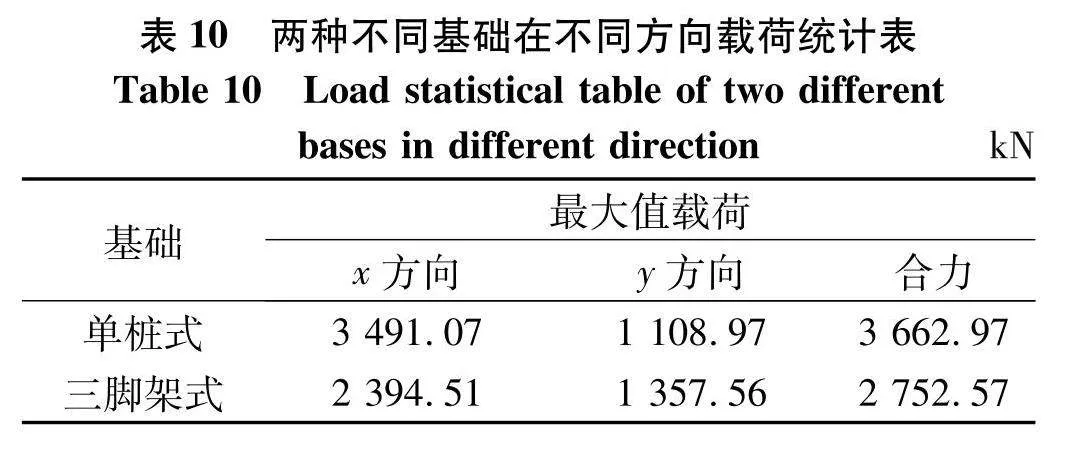
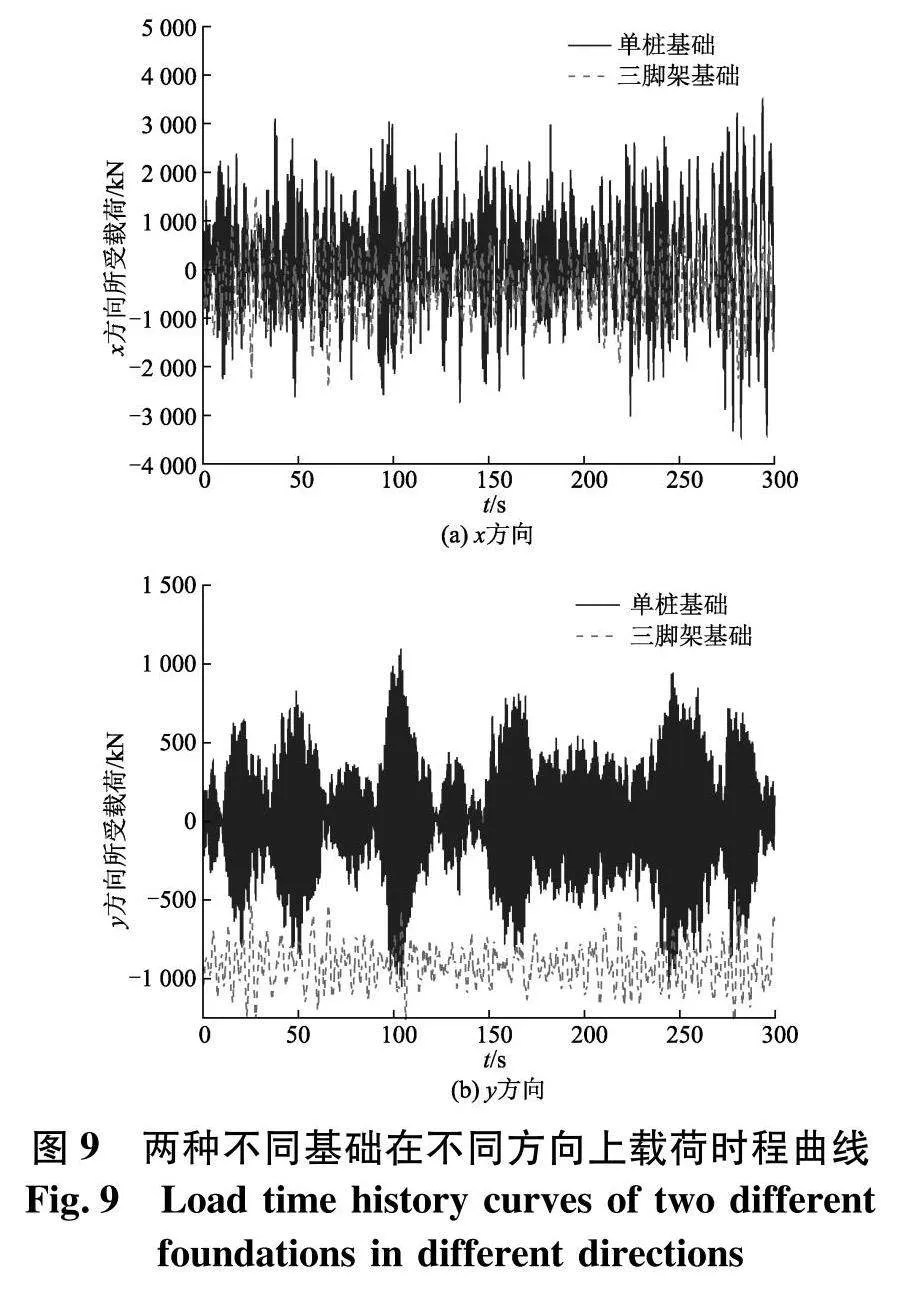
由于风机基础与土体之间存在着相互作用[16],所以当基础所受载荷过大时,容易造成桩基不稳的现象,所以文中对单桩基础和三脚架基础底部受力最大的单根竖直支撑桩进行了载荷分析,结果如图9,表10为不同方向两种基础所受载荷最大值的统计表.
由图9和表10可知,在水平面内单桩式风机基础所受合力比三脚架式风机基础高33.07%,其主要是因为单桩基础所受的载荷由单一的中心钢管承受,所以塔筒和基础的位移以及载荷响应较大,而三脚架式风机底部由多根垂直以及倾斜套管组成三脚架式支撑结构,不仅可以加强基础周围结构的强度和刚度还会分散由中心钢管承受的上部塔架载荷,可以较好地提升风机整体的动态性能.
3 结论
运用GH Bladed软件以NERL 5MW风机为目标风机,对单桩式风机以及三脚架式风机的动态响应进行了对比分析,主要结论:
(1) 根据NREL所提供的风机参数,在GH Bladed中建立了风、浪、流与风机结构全耦合分析模型,研究了两种形式的风机在所选海况下的动态响应.
(2) 单桩式风机叶片叶根处推力和弯矩的最大值比三脚架式风机高30.8%和48.6%,三脚架式风机叶根推力和弯矩的平均值比单桩式风机高32.97%和48.46%,可以得到单桩式风机标准差比三脚架式标准差高49.82%和21.27%,说明单桩式风机叶根处推力值和弯矩值浮动较大,单桩式风机比三脚架式风机叶尖位移最大值高44.32%,所以单桩式风机叶片叶根处损伤或折断的几率更大.单桩式风机塔顶和塔中位移最大值比三脚架式最大值高83.7%和65%,单桩式风机塔顶和塔中位移平均值是三脚架式风机的3.4倍和3倍,在水平面内单桩式风机基础所受合力也比三脚架式高33.07%,所以三脚架式风机动态响应结果更好,整体结构稳定性高于单桩式风机.
(3) 从文中研究结构可以发现,在所选的北太平洋海况下三脚架基础从叶片、塔筒、基础的位移和载荷响应都较单桩基础响应更优,且单桩式风机基础对基岩层距离有一定要求,如果仅从安全性考虑三脚架基础响应值更小,安全性更高.但另外一方面,单桩基础结构简单,对海床和水平度要求较低,制造和安装成本也较低,经济性更好.
(4) 安全性和经济性都是风机选型的重要指标,目前难以简单根据某种指标进行选择,未来研究中可建立以经济性和安全性两个优化目标的综合优化选择数学模型,进行更进一步的风机优化选型分析.
参考文献(References)
[1] 杨光俊.我国风电绿色发展前景分析和政策建议[J].环境保护,2018,46(2):17-19.
[2] 陈大江,王皓,许海波,等.海上风电变径单桩基础动力响应分析[J].水力发电,2023,49(1):88-93.
[3] 徐彬,薛帅,高厚磊,等.海上风电场及其关键技术发展现状与趋势[J].发电技术,2022,43(2):227-235.
[4] 陈凤云,王振扬,苏凯.海上风机单桩基础与塔筒间连接方式对比研究[J].中国农村水利水电,2023(2):200-203,210.
[5] 蘧鑫晨.海上风机三脚架基础水动力特性试验及数值研究[D].杭州:浙江大学,2019.
[6] 郝二通,王未,王铭.海上风电机组单桩基础和三脚架基础抗撞性能研究[J].装备环境工程,2020,17(7):6-11.
[7] 徐亚洲,段静.近场地震作用下近海单桩风机动力响应分析[J].振动与冲击,2022,41(23):222-229,240.
[8] 李琪,周文杰,童建国,等.台风环境中典型海上风机结构的动力响应数值分析[J].中国海洋平台,2019,34(3):32-39.
[9] MARDFEKRI M,GARDONI P.Probabilistic demand models and fragility estimates for" offshore wind turbine support structures[J].Engineering Structures,2013,52:478-487.
[10] JONKMAN J, BUTTERFISLD S, MUSIAL W,et al. Definition of a 5-MW reference wind turbine for offshore system development[M]. United States:[s.n.], 2009.
[11] 刘伟.海上风电单筒多舱基础地基参数反演及动力响应研究[D].天津:天津大学,2001.
[12] 林毅峰.海上风电机组支撑结构与地基基础一体化与分析设计[M].北京:机械工业出版社,2020.
[13] 江俊杰. 导管架风机基础加装养殖网箱方案设计及力学性能分析[D].镇江:江苏科技大学,2017.
[14] 贺赛坪. 海上浮式风机系泊缆索动张力特性分析[D].长沙:湖南科技大学,2016.
[15] 兰德尔. 海洋工程基础[M]. 上海:上海交通大学出版社, 2002.
[16] 郭健,王皓,骆光杰,等.海上风机变径单桩基础水平承载特性数值分析[J].科学技术与工程,2022,22(9):3658-3664.
(责任编辑:贡洪殿)
