基于Python的光学现象可视化分析

2024-01-11任刘娜付文慧苏艳丽姜其畅

大学物理实验 2024年1期

任刘娜,付文慧,苏艳丽,姜其畅

(运城学院物理与电子工程系,山西运城 044000)

随着信息技术的不断发展,越来越多的研究人员将C语言、VB语言、MATLAB等计算机编程语言引入到了光学相关实验现象的模拟仿真当中[1-5]。目前,在大数据分析和网络运维的主流编程中,Python语言的使用已经非常广泛[6-7]。但是关于光学干涉、衍射现象的可视化研究多是采用MATLAB语言[8-10],而基于Python语言的多光学现象仿真研究还相对较少。相较于其它语言,Python语言是一种开源免费的程序设计语言,它具有简单易学的特点。在使用Python语言编写程序时不需要考虑底层的细节问题,而且Python第三方库丰富且调用简单,同时可以调用第三方库的函数直接使用,从而提高编程的效率。本文利用PyCharm软件,基于Python语言及其扩展库中的Numpy、Matplotlib实现了对典型光学问题的可视化分析,分别对杨氏双缝干涉实验和夫琅禾费单缝衍射实验进行了可视化研究,相关的分析方法还可以推广到其他光学现象或者物理现象的研究中。

1 杨氏双缝干涉实验

1.1 理论分析

杨氏双缝实验是最早证明光的波动性的经典实验之一,其原理是光波的叠加。杨氏双缝干涉实验装置如图1所示,用平行光照射,光到达第一个狭缝,可视为光源S。根据惠更斯-菲涅尔原理,光源S相当于次波源,继续发射球面波,再经过距离较小的双缝S1和S2,双缝间距用d表示,即可获得相干光源。距离双缝为D的观察屏P上可以观察到亮暗相间的条纹,条纹间距为Δy。

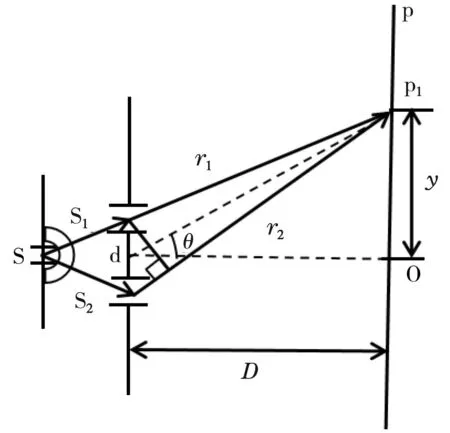
图1 杨氏双缝干涉实验装置示意图

用r1和r2分别表示S1和S2与P间的距离,在D>>d的情况下,其光程差为

(1)

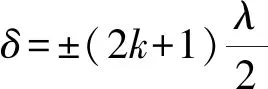
(2)

为了使干涉图样的计算简化,把S及S1和S2均视为单色光源,则可计算屏幕P点处的光强为[11]

(3)

1.2 可视化分析

根据杨氏双缝干涉公式,可知影响干涉条纹分布的参数为λ、d、D等。结合输入参数和输出图像的需求,利用Python语言及其内置的扩展库,可以方便快捷地完成实验要求,设初始光强I1=1,以下是关键代码及其注释:

D=400#双缝和屏幕的距离,单位为毫米

d=0.2#双缝之间的距离

λ=600e-6 #入射光波长

x=np.arange(-2,2,0.0001) #设置x轴取值范围

θ=(2*np.pi*d*x)/(λ*D) #计算相位差

θ[θ==0]=np.finfo(float).eps #避免最大值出现零

I=4*np.cos(θ/2)**2#计算干涉光强度分布

plt.figure( ) #创建图形窗口

plt.plot(x,I,′:′,linewidth=2) #画曲线

plt.legend( )

plt.xlabel(u′y/mm′,fontproperties=’simHei′,fontsize=20) #横坐标及字体

plt.ylabel(u′光强/a.u.′,fontproperties=’simHei′,fontsize=20) #纵坐标及字体

图2表示杨氏双缝干涉的光强分布,实验参数选定为λ=600 nm,双缝间距d=0.2 mm,缝屏距D=400 mm。由图2可以看出双缝干涉实验中各级亮条纹的光强以及条纹间隔基本相等。

y/mm

为了方便展示条纹间距与波长λ、双缝间距d及缝屏距D的关系,可采用控制变量法探究杨氏双缝干涉的结果与波长、双缝间距和缝屏距的关系。

(1)不同波长λ及双缝间距d下的杨氏双缝干涉光强分布

首先控制三种光波长λ和缝屏距D不变,改变双缝间距d。实验参数选定为λ1=450 nm,λ2=550 nm,λ3=660 nm,D=400 mm,变量选取d1=0.1 mm,d2=0.2 mm,d3=0.3 mm。可得图3所示不同d下的杨氏双缝干涉光强分布。

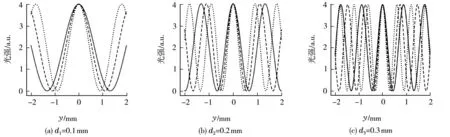
图3 不同双缝间距d下的杨氏双缝干涉光强分布(━λ=660 mm,┅λ=550 mm,┉λ=450 mm)

由图3可以看出不同双缝间距下杨氏双缝干涉光强分布会发生改变,用Δy蓝1、Δy蓝2、Δy蓝3,Δy绿1、Δy绿2、Δy绿3,Δy红1、Δy红2、Δy红3,分别表示λ1=450 nm,λ2=550 nm,λ3=660 nm时对应d1=0.1 mm,d2=0.2 mm,d3=0.3 mm的条纹间距,由图像信息可得:Δy蓝1>Δy蓝2>Δy蓝3,Δy绿1>Δy绿2>Δy绿3,Δy红1>Δy红2>Δy红3,且有Δy蓝1<Δy绿1<Δy红1,Δy蓝2<Δy绿2<Δy红2,Δy蓝3<Δy绿3<Δy红3。

利用公式(2)可以求得:Δy蓝1=1.80 mm,Δy蓝2=0.90 mm,Δy蓝3=0.60 mm,即Δy蓝1>Δy蓝2>Δy蓝3;Δy绿1=2.20 mm,Δy绿2=1.10 mm,Δy绿3=0.73 mm,即Δy绿1>Δy绿2>Δy绿3;Δy红1=2.64 mm,Δy红2=1.32 mm,Δy红3=0.88 mm,即Δy红1>Δy红2>Δy红3,且有Δy蓝1<Δy绿1<Δy红1,Δy蓝2<Δy绿2<Δy红2,Δy蓝3<Δy绿3<Δy红3,仿真结果与理论分析的结果相符合。由此可帮助我们更好的理解波长和双缝间距在改变杨氏双缝干涉图样中的作用:干涉条纹间距随着波长的增大而增大,随着双缝间距的增大而减小。

(2)不同缝屏距D下的杨氏双缝干涉光强分布

控制三种光波长λ和双缝间距d不变,改变D。实验参数选定为λ1=450 nm,λ2=550 nm,λ3=660 nm,d=0.2 mm,变量选取D1=200 mm,D2=400 mm,D3=600 mm。可得如图4所示在不同D下的杨氏双缝干涉光强分布。

图4 不同缝屏距D下的杨氏双缝干涉光强分布(━λ=660 mm,┅λ=550 mm,┉λ=450 mm)

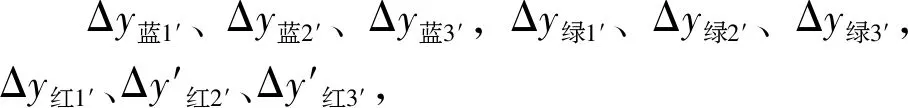
同样利用公式(2)可以求得:Δy蓝1′=0.45 mm,Δy蓝2′=0.90 mm,Δy蓝3′=1.35 mm,则有Δy蓝1′<Δy蓝2′<Δy蓝3′;Δy绿1′=0.55 mm,Δy绿2′=1.10 mm,Δy绿3′=1.65 mm,则有Δy绿1′<Δy绿2′<Δy绿3′;Δy红1′=0.66 mm,Δy红2′=1.32 mm,Δy红3′=1.98 mm,则有Δy红1′<Δy红2′<Δy红3′,仿真图像结果与理论分析的结果相符合。由此可帮助我们理解缝屏距也是改变杨氏双缝干涉光强图样的因素之一,干涉条纹间距随着缝屏距的增大而增大。

2 夫琅禾费单缝衍射实验

2.1 理论分析

夫琅禾费单缝衍射是光源和观察屏都距衍射屏无限远时的衍射即远场衍射,其实验装置如图5所示,光源S后放置透镜L1,当点光源S的光通过透镜L1后会形成一束平行光,该束平行光垂直通过间距大小为a的缝隙时在一定条件下就会发生衍射现象,衍射光线经过透镜L2会汇聚到接收屏F上形成衍射条纹。接收屏F垂直于透镜的光轴,因此观察屏上会出现以单缝为中心的对称分布的亮暗相间衍射条纹。

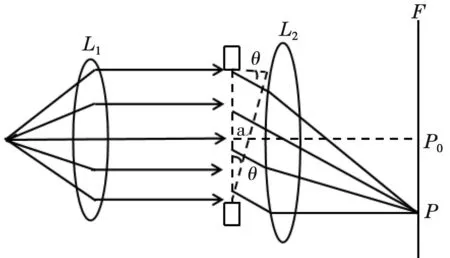
图5 夫琅禾费单缝衍射实验装置示意图

菲涅尔提出将波阵面分割成许多等面积的半波带,由半波带的数量N和光程差a·sinθ可以推测出衍射条纹的亮暗。在夫琅禾费单缝衍射中,半波带数为

(4)

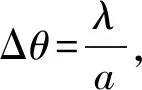
(5)

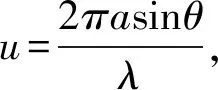
(6)

2.2 可视化分析

根据夫琅禾费单缝衍射公式,可知影响衍射条纹分布的参数为a、λ等。结合输入参数和输出图像的需求,利用Python语言及其内置的扩展库,可以方便快捷地完成实验要求。设初始光强I0=1,图6表示夫琅禾费单缝衍射的光强分布,实验参数选定为λ=660 nm,单缝大小为a=0.05 mm。可以看出中央亮条纹两侧光强迅速减弱,直至第一条暗条纹出现,其后,光强又会逐渐增大成为一级亮条纹,以此类推。各级亮条纹的光强会随着级数的增大而减弱,中央亮条纹是最宽的且光强是最大的。

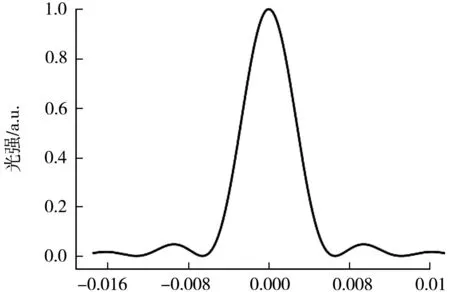
θ/rad

为了方便理解中央亮条纹的角宽度与单缝大小a、波长λ的关系,同样采用控制变量法探究夫琅禾费单缝衍射的结果与单缝大小、波长的关系。

(1)不同波长λ下的夫琅禾费单缝衍射光强分布

控制a不变,改变波长λ。实验参数选定为a=0.05 mm,变量选取λ1=450 nm,λ2=550 nm,λ3=660 nm,可得如图7所示的三种波长下的夫琅禾费单缝衍射光强分布。

θ/rad

可以看出不同波长入射下夫琅禾费单缝衍射光强分布会发生改变,用Δθ蓝、Δθ绿、Δθ红分别表示λ1=450 nm,λ2=550 nm,λ3=660 nm时的中央亮条纹的半角宽度,由图像信息可得Δθ蓝<Δθ绿<Δθ红。

利用公式(5)可以求得:Δθ蓝=0.009 rad,Δθ绿=0.011 rad,Δθ红=0.013 2 rad,则有Δθ蓝<Δθ绿<Δθ红,仿真图像与理论分析的结果相符合。由此可帮助我们理解入射光波长在改变夫琅禾费单缝衍射光强分布图样中的作用:中央亮条纹的半角宽度随着波长的增大而增大。

(2)不同单缝a下的夫琅禾费单缝衍射光强分布

控制波长λ不变,改变a。实验参数选定为λ1=450 nm,λ2=550 nm,λ3=660 nm,变量选取a1=0.03 mm、a2=0.06 mm、a3=0.09 mm,可得如图8所示的单缝衍射图样。

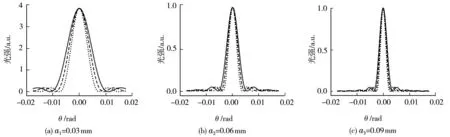
图8 不同单缝a下的夫琅禾费单缝衍射光强分布(━λ=660 mm,┅λ=550 mm,┉λ=450 mm)

可以看出改变单缝大小,相应的夫琅禾费单缝衍射光强分布就会随之发生变化。用Δθ蓝1、Δθ蓝2、Δθ蓝3,Δθ绿1、Δθ绿2、Δθ绿3,Δθ红1、Δθ红2、Δθ红3,分别表示λ1=450 nm,λ2=550 nm,λ3=660 nm时对应a=0.03 mm、a=0.06 mm、a=0.09 mm的中央亮条纹的半角宽度,由图像信息可得Δθ蓝1>Δθ蓝2>Δθ蓝3,Δθ绿1>Δθ绿2>Δθ绿3,Δθ红1>Δθ红2>Δθ红3。

同样利用公式(5)可以求得:Δθ蓝1=0.015 0 rad,Δθ蓝2=0.007 5 rad,Δθ蓝3=0.005 0 rad,则有Δθ蓝1>Δθ蓝2>Δθ蓝3;Δθ绿1≈0.018 3 rad,Δθ绿2≈0.009 2 rad,Δθ绿3≈0.006 1 rad,则有Δθ绿1>Δθ绿2>Δθ绿3;Δθ红1=0.022 0 rad,Δθ红2=0.011 0 rad,Δθ红3≈0.007 3 rad,则有Δθ红1>Δθ红2>Δθ红3,仿真图像与理论分析的结果相符合。由此可帮助我们理解单缝大小也是改变夫琅禾费单缝衍射光强分布的因素之一,中央亮条纹的半角宽度随着a的增大而减小且衍射条纹都会向中央亮条纹处靠近。