替代法测量改装表内阻的误差分析

刁宇轩,邹宸钰,王嘉睿,谢晓梅,熊水兵,杨利建

(华中师范大学 物理科学与技术学院,湖北 武汉 430079)

电表改装与校准是大学物理实验课程中常见的基础实验[1,2],该实验将量程较小的微安表扩程为量程较大的电流表或电压表,并且进行校准[3]。在整个实验过程中,扩程电阻的大小与表头内阻大小直接相关。因而测量表头内阻至关重要,这一步骤对改装电表的精确程度有着巨大的影响。在实验中,测量表头内阻一般采用半偏法和替代法两种方法。半偏法需要考虑在并联了改装表之后,系统总电阻的变化引入的系统误差,是很多文献探讨较多的一种[4]。而替代法简单直观,普遍认为测量精度较高,讨论较少[5]。

但是,在替代法测量内阻实验时发现,在一定范围内改变替代的电阻阻值,干路中标准表的读数基本不变。这个替代电阻不可确定的范围可以达到100 Ω这样大的值。微安表的内阻在2 000 Ω左右,这样用替代法测量误差接近5%。有研究指出,电源电压的大小对测量误差产生了影响,并得出了电源电压越大,会导致内阻测量误差越大的结论[6]。该方法可以有效的提高替代法测量内阻的精度,但是没有指出测量误差减小的原因。本文根据替代法电路中所使用的各个仪器精度,计算了标准表、电阻箱等实验中所用仪器引入的不确定度。在理论分析的同时,对结果也进行了实验验证。

1 替代法测量表头内阻实验的分析

1.1 实验思路

替代法测内阻的实验中,被改装的微安表(表头G)的量程为100 μA,精度2.5级。标准微安表有100 μA,200 μA,500 μA,1000 μA四个量程,实验中用100 μA量程,精度0.5级。电路如图1所示,其中E是电压可调的直流电源,R为电源内阻。Rw是保护电阻,R1是替代电阻,保护电阻和替代电阻我们都采用电阻箱。实验中我们采用了ZX38A/11型交直流电阻箱。Rg和R0分别是待测被改装表和标准微安表的内阻。

图1 替代法测量表头内阻电路图

实验时,将双向开关调到“a”,调整保护电阻Rw阻值,记录标准表示数I;将双向开关调到“b”,保持电源电压E和保护电阻Rw不变,调整替代电阻R1的阻值,当标准表示数为I时,替代电阻的阻值即为电流计内阻[3],即:

Rg=R1。

(1)

1.2 测量方法改进分析

理想情况下,替代电阻的阻值与表头内阻相同。但是,若标准表灵敏度不高,可能出现这样的情况:调整替代电阻阻值,电路中的电流大小也确实发生微小改变,但标准表的指针却没有偏转或者偏转程度无法用肉眼判断[5]。下面讨论如何减少这一误差。

当开关K置于“b”时,有:

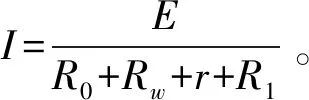
(2)

当替代电阻R1的改变量为dR1时,I的改变量为

(3)

联立(2)式和(3)式,得:

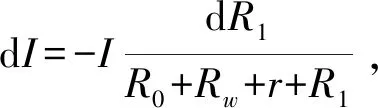
即:

(4)

由式(4)可知,当dI为标准表可分辨的最小电流变化,dR1即为替代电阻不可确定的范围。要使dR1减小,有以下三种方法:

①减小R0和r,也就是选择内阻小的标准表和电源;

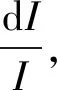
③减小保护电阻Rw的阻值。

1.3 不确定度计算

下面我们计算替代法测量中的不确定度。替代法的公式(1)很简单,按照此公式B类不确定度只需计算由替代电阻R1引入的不确定度。但是,在实际调节中,我们是需要判断开关打到“b”的位置时,标准电流表读数是否完全相同。所以,标准电流表读数的不确定性也会引入误差[8]。标准表的作用类似于惠斯通电桥实验中检流计的作用,所以标准表引入的不确定度我们借鉴了电桥灵敏度[9],计入电阻的不确定度中。电流表灵敏度可按下述方法计算:测得电流改变1 μA时,标准表指针偏转格数Δd,电路的电阻Rw的变化量ΔRw,则S定义为

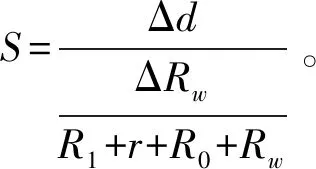
(5)

在实验中由于标准表灵敏度而引入的不确定度ΔRs可用下述公式估算:

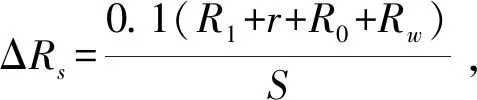
(6)

其中,0.1的取值是表示对最小刻度进行1/10估算。实验中所用标准表的指针与刻度线都比较细,偏转较明显,所以可以进行十分之一估读。计算联立(5)(6),得:

(7)

因此,该实验B类不确定度可表示为

(8)

2 实验装置与实验步骤

2.1 实验装置

表头一个,直流稳压电源一台,标准电流表一只,电阻箱两只,单刀双掷开关一个,连接导线若干,实验用9孔插件方板一块。(下方图2为实验电路,图3展示了电阻箱型号等细节)

图2 替代法测量表头内阻实物图

图3 实验用电阻箱型号与准确度等级

2.2 实验步骤

2.2.1 改装表内阻的测量

① 按图1所示连接电路;

② 将开关掷向“a”,调节Rw使标准表示数为100 μA,记录此时E,Rw的值;

③ 将开关掷向“b”,保持Rw的值不变,调节R1的值,使标准表示数仍为100 μA,记录此时R1的值;

④ 稍稍改变R1的值,保证标准表未发生肉眼可见的偏转,并记录阻值范围R1 min和R1 max;

2.2.2 用于评定不确定度的相关测量

⑤ 改变电阻Rw使电流变为99 μA,并记录电阻改变量ΔRw;

⑥ 改变电源电压,重复步骤②～⑤。

3 数据处理

3.1 数据测量及不确定度计算

实验数据如下表1,其中E为路端电压,R1 min和R1 max为替代电阻R1在保持标准表读数不变情况下的最小值和最大值,Rw为保护电阻阻值。ΔRw表示的是在该电路下使标准表指针偏转最小刻度一格(1 μA),电阻Rw的改变量。

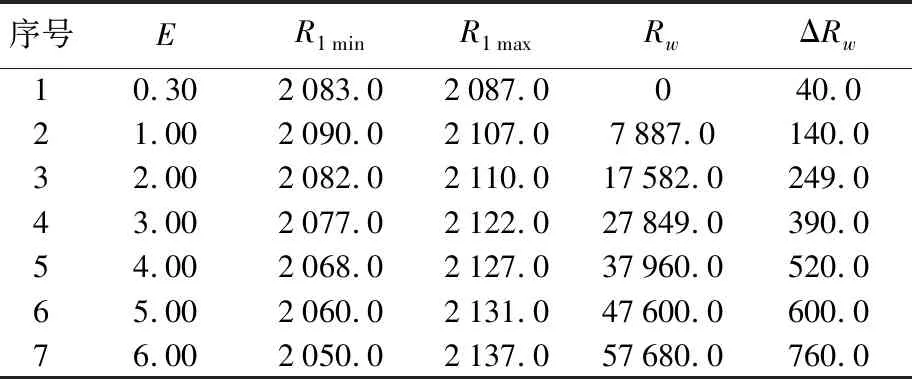
表1 替代法测量电阻原始数据表格(电压单位为伏特,电阻单位为欧姆)

实验测得改装表内阻的不确定值表示如下:

ΔRg测=R1 max-R1 min,

(9)

替代法测量改装表内阻的值取测量最大值和最小值的均值,即

Rg=R1=(R1 min+R1 max)/2 ,

(10)

因为电流表引入的不确定度为

由电阻箱各旋钮不确定度计算得R1电阻箱引入的不确定度ΔR1为

ΔR1=2090×0.1%+9×0.5%+0.5×2%≈2.14 Ω

则可推算出该组实验测量改装表内阻Rg的B类不确定度为

计算出该电路下测量表头内阻的范围大小应为

|2ΔRg|=45.2 Ω ,

测量表头内阻R1 max读数为2 122.0 Ω,R1 min读数为2 077.0 Ω,表头内阻实际测量值的范围为

ΔRg测=2122.0-2077.0=45.0 Ω 。

理论值与实际值之差为

|2ΔRg|-ΔRg测=0.2 Ω 。

按上述方法所得数据列如表2所示。

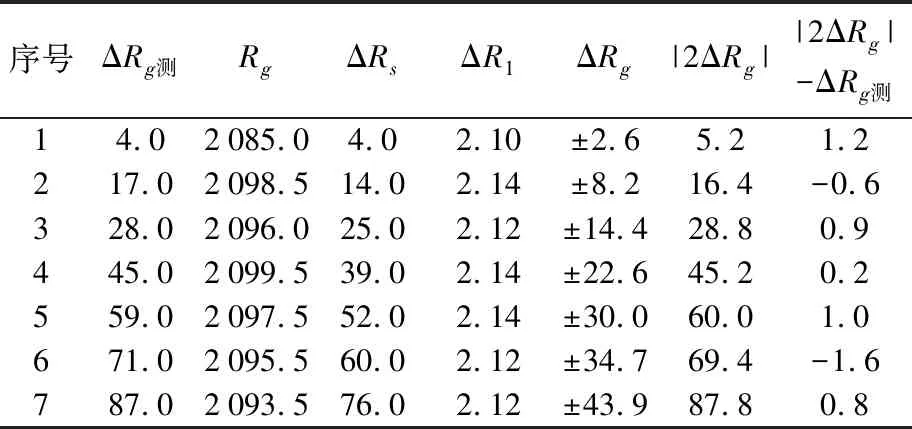
表2 数据处理表格(电阻单位为欧姆)

以路端电压E为横坐标,以ΔRg测和|2ΔRg|为纵坐标,绘制实验值与计算值如图4。

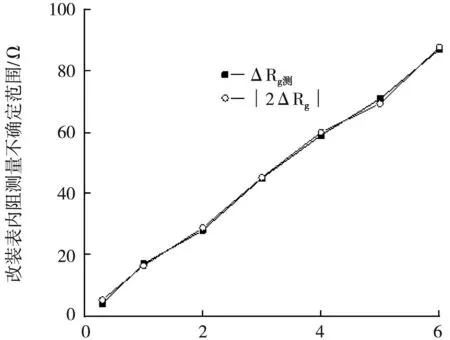
E/V

从图4可以看出,随着电源电压的增加,替代法测量内阻的不确定度会单调增加。另外,由表格2中数据可见,不确定度的理论值与实验测量值之差|2ΔRg|-ΔRg测都是比较小的,理论分析和实验测量吻合较好,也说明引入电表的灵敏度来计算电阻的合成不确定度是合理的。

在第一组实验数据中,通过直接调节电源电压来控制标准表示数基本处于100.0 μA附近,并没有用到保护电阻。在误差允许的范围内,可以认为此时测量电阻的误差达到了最小。

后六组实验数据中,控制标准表示数保持在100.0 μA,调节替代电阻阻值R1,测量不同电压下表头内阻的阻值。实验中可以明显看出,电源电压增大导致我们不得不增大保护电阻阻值Rw,最终导致不确定度ΔRg增大,使得测量误差增大了。

3.2 实验中存在的其他误差分析

本实验误差主要来自于所用的电阻箱产生的误差,实验过程中调节0.1 Ω旋钮指针偏转不明显,导致难以将测量结果进一步精确。

另外标准表读数所产生的误差也不可被忽略,由于标准表指针和刻度的构造,在替代前后,难以将标准表刻度准确无误地始终控制在同一位置,因而产生了部分误差,而这部分误差又难以通过不确定度公式计入,因而最终测量结果误差大于了理论计算出的误差。

本实验最后一组采用直接控制电源电压的方式,而电源电压本身难以调节,其精度无法精确到0.1 V以下,因而导致了误差。

4 结 论

本文通过理论分析和实验验证,得出了替代法测量表头内阻的实验中,若电源电压越大,保护电阻就要增大,进而导致测得的表头内阻误差增大。其中保护电阻是产生测得表头误差的本质原因。所以,在大学物理实验教学过程当中,在保护各个实验元件安全条件下,应尽量选择较小的电源电压,使待测表头刚好满偏为宜,这样就尽可能地减小了保护电阻阻值,达到了减小测量误差的目的。