弹簧耦合摆在复杂情况下的小振动解

高金泽 王爱记

(北京师范大学物理学系 北京 100875)

自然界中相互作用的振动系统非常普遍,如电学中电容和电感耦合的振荡回路[1]、固体晶格中相邻原子的振动模式[2]以及光子和声子耦合产生的电磁耦合场[3]等.相互作用将使振动系统呈现丰富的运动学行为,因此对其研究十分必要.在力学中,弹簧耦合摆也属于此类系统.由两个单摆悬挂于同一水平线上,两摆球以弹簧连接,实现振动的相互耦合.

目前关于弹簧摆的研究文章中,大多针对两摆悬挂点间距离恰好等于弹簧原长的情况进行研究[4-6],具有一定局限性.当两单摆悬挂点间的距离略大于或小于弹簧原长时,平衡状态下单摆在竖直方向的角度偏移使动能和势能的表达式更为复杂,呈现的拍现象也受更多因素的影响.本文从两摆间距离略大于弹簧原长的情况入手,在小角度近似的情况下从分析力学的角度进行求解.笔者利用MATLAB计算了非小角度近似下的数值解,对其运动产生的拍进行探究,与两摆间距离等于弹簧原长的情况对比.对于两摆间距离略小于弹簧原长也可以用类似的求解方法.

1 模型构建

图1为弹簧摆在静止状态下的示意图.轻质弹簧劲度系数均匀为κ,轻质摆线长l,小球A,B均视为质点,质量均为m,初始偏角均为θ0,两摆悬挂点间距离为L,弹簧自然长度L0,L0略小于L,所需物理量均在图中标出.

假设不考虑外界空气阻力等耗散影响,弹簧与小球在竖直平面内运动.两摆的角度取逆时针为正方向,处于平衡状态时,设弹簧压缩量为Δx0,小球A的平衡角度为+θ0,小球B的平衡角度为-θ0.

图1 静止状态下系统示意图

由虚功原理得

mgδy+κΔx0δx=0

(1)

又有

δy=lδcosθ0

Δx0=L-2lsinθ0-L0

δx=lδsinθ0

(2)

联立式(1)、(2),设l0=L-L0,则有

mgtanθ0=κ(l0-2lsinθ0)=κΔx0

(3)

如图2所示设摆线偏离平衡位置的角度为θ1、θ2.

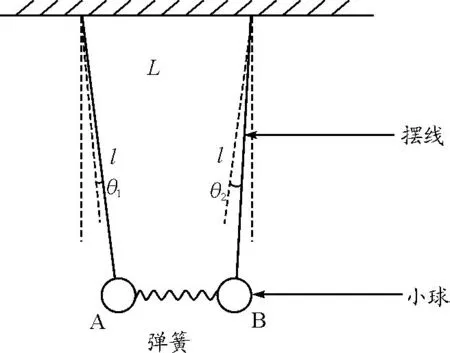
图2 运动过程中系统示意图(图中两小球偏离竖直

则小球A的位置坐标为

y1=-lcos(θ0+θ1)

B的位置坐标为

设悬挂点所在的水平线为重力势能零点,系统平衡状态下的弹簧弹性势能为弹性势能零点,则系统的动能T、重力势能Vg和弹性势能Vk满足

(4)

Vg=mg(y1+y2)

(5)

(6)

(7)

Δx,Δy可表示为

(8*)

即

(8)

对式(5)小量展开可得

式(3)、(8)代入式(7)可得

(10)

联立式(9)、(10),令V=Vg+Vk,则可得

(11)

其中

(12)

(13)

2 简正分析

2.1 求解简正频率

拉格朗日量L中含有关于坐标θ1、θ2的耦合项,在求解问题时,往往通过构造矩阵V和T求解简正频率进而求解简正坐标.

由式(4)、(11),列出势能、动能对应的矩阵[7]

(14)

并记P=V-ω2T,令det(P)=0,得

解得系统的简正频率

(15)

由于

又C<0,故ω1、ω2均为实数,且ω1<ω2.

2.2 构造简正坐标

代入简正频率ω后,矩阵P的本征矢量即为原广义坐标线性组合的系数,如此可得到各简正频率ω对应的简正坐标.

当ω=ω1时,代入矩阵P得

其特征向量n1=(1,1).

当ω=ω2时,代入矩阵P得

其特征向量n2=(1,-1).

所以对应ω1的简正坐标为ξ1=θ1+θ2,对应ω2的简正坐标为ξ2=θ1-θ2.

将ξ1、ξ2代入拉格朗日量得

(16)

得到拉格朗日运动方程

(17-1)

(17-2)

可以通过求解式(17-1)、(17-2),验证其对应的简正频率正是式(15)中的ω1、ω2.

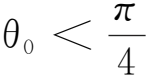
2.3 近似解与非近似解的对比

非近似解对动能T、势能V中的小量θ1、θ2不做近似处理.

根据

Vg=mg(y1+y2)

得到拉格朗日量

L=T-(Vg+Vk)

通过MATLAB中的ode45解拉格朗日运动方程得到数值解.

图3 取时θ1、θ2的近似解与非近似解

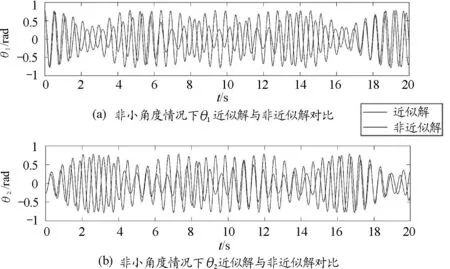
图4 取时,非小角度情况下近似解与非近似解对比

3 与摆悬挂点间距等于弹簧原长情况的对比

当两单摆悬挂点间距等于弹簧原长时,弹簧耦合摆的运动依旧形成拍.摆悬挂点间距等于弹簧原长时,简正频率[6]为

(18)

由式(21),可以得到拍频ω0

(19)

当2κl≪mg时,对ω0进行小量展开得到

图5 取ωp=10 rad/s时,ω0小量展开的近似解与标准解对比

当ωs逐渐增大,2κl≪mg的条件不再满足,小量展开的近似解与标准解曲线出现偏差.

摆悬挂点间距大于弹簧原长时,由式(18)得拍频ω>为

(21)

当2κl≪mg时,对ω>进行小量展开

(22)

故拍频ω除正比于弹簧的固有频率ωs的二次方,反比于单摆固有频率ωp外,还与平衡状态时的偏移角度θ0有关.

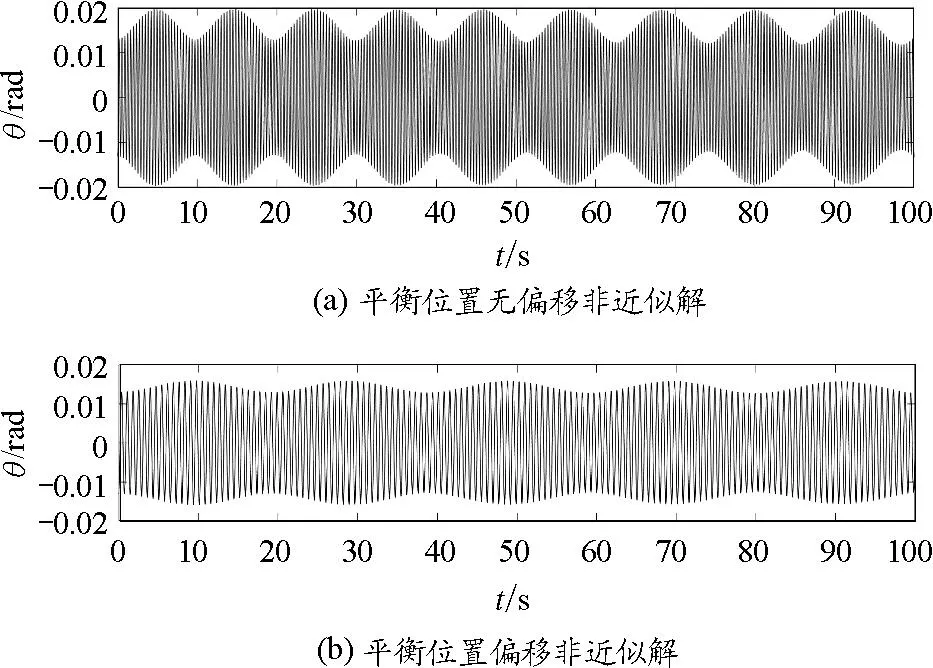
图6 2κl≪mg情况下拍频对比图

图6验证了上述结论,即在其他条件相同情况下,两单摆悬挂点间距等于弹簧原长的情况下,拍频恒大于悬挂点距离大于弹簧原长的情况.

4 总结

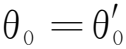
在非小角度情况下,将近似解和非近似解的运动图像进行对比,发现近似解的拍频稍大于非近似解,近似计算不再合理.

在2κl≪mg的条件下,耦合摆运动的拍频满足式(25),即拍频正比于弹簧的固有频率ωs的二次方,反比于单摆固有频率ωp,且与平衡状态时偏移角度θ0有关.两单摆悬挂点间距等于弹簧原长系统的拍频恒大于悬挂点距离大于弹簧原长的系统.