弹簧振子类试题数据设计的自洽性研究

2024-01-11何崇荣

物理通报 2024年1期

何崇荣张黎

(武汉市黄陂区第一中学湖北武汉 430300)

弹簧振子是高中阶段的一个重要物理模型,借助该模型可以考查牛顿运动定律、动量和能量等高考主干知识.然而在命制弹簧振子类试题设计数据时容易想当然,造成数据不自洽.下面结合具体的两个案例,分别给出单弹簧振子和双弹簧振子类试题数据设计是否自洽的论证方法.

1 弹簧连一物体的单振子

【例1】如图1(a)所示,在倾角为37°足够长的粗糙斜面底端,一质量m=1 kg的滑块压缩着一轻弹簧且锁定,但它们并不相连,滑块可视为质点.t=0时解除锁定,计算机通过传感器描绘出滑块的v-t图像如图1(b)所示,其中Oab段为曲线,bc段为直线,在t1=0.1 s时滑块已上滑x=0.2 m的距离(取g=10 m/s2,sin 37°=0.6,cos 37°=0.8).则( )

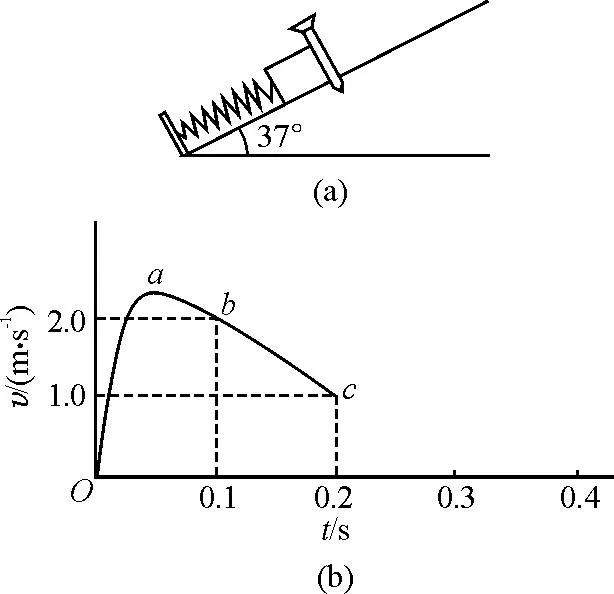
图1 例1题图

A．滑块与斜面之间的动摩擦因数μ=0.1

B．滑块与斜面之间的动摩擦因数μ=0.2

C．t=0.4 s时滑块的速度大小为1.0 m/s

D．0～0.1 s内弹簧弹力做功4 J

解析：由题意可知,滑块在t1=0.1 s时与弹簧分离,之后沿斜面向上做匀减速,根据牛顿第二定律有

mgsinθ+μmgcosθ=ma1

由图1(b)可知

于是解得

μ=0.5

在0～0.1 s内,根据动能定理有

解得

W=4 J

滑块沿斜面下滑过程,根据牛顿第二定律有

mgsinθ-μmgcosθ=ma2

滑块与弹簧分离后,沿斜面向上运动时间t3,则

vb=a1t3

t=0.4 s时滑块的速度

v=a2(t-t3)

解得

v=2 m/s

所以正确选项为D.

疑问：题目给出的条件是否存在不自洽问题?

滑块沿斜面向上的运动为简谐运动,以平衡位置为原点,沿斜面向上为正方向,设t=0时滑块距离弹簧原长处的距离为d,振幅为A,周期为T,则滑块偏离平衡位置的位移

x=-Acosωt

速度

v=ωAsinωt

其中

t1=0.1 s时,滑块位移

x1=-Acosωt1=d-A

(1)

滑块速度

vb=ωAsinωt1

(2)

已知

d=0.2 mt1=0.1 s

vb=2 m/sT>0.1 s

可以求出A与ω,具体求解如下.

由式(1)得

将其代入式(2)得

(3)

物体在平衡位置时

mgsinθ+μmgcosθ=κx1=κ(d-A)

(4)

解得

代入数据,结合T>0.1 s,利用式(3)由数值计算可得

ω=23.3 rad/s

此时A=0.118 m,μ=4.815,而根据图1(b)中的bc段可得μ=0.5,两者相矛盾,所以题目数据设计不自洽.

也可以通过图1(b)中bc段的条件:t1=0.1 s时,vb=2 m/s;t2=0.2 s时,vc=1 m/s,来验证0.1 s内物体运动距离d是否等于0.2 m,具体验证如下:

设0.1～0.2 s内滑块加速度大小为a,根据牛顿第二定律有

a=g(sinθ+μcosθ)=10 m/s2

(5)

联立式(1)、(2)、(4)、(5)解得

(6)

(7)

代入数据,结合T>0.1 s,利用式(6)由数值计算可得ω=18.35 rad/s,此时d=0.143 m.这与题目给出d=0.2 m相矛盾,说明数据设计不自洽.

改进方案：要么不用给出在t1=0.1 s时滑块已上滑距离d(题目中用x表示)的值,就用字母表示,这样计算0～0.1 s内弹簧弹力做功用d表示即可.或者通过已知t1=0.1 s时vb=2 m/s,t2=0.2 s时vc=1 m/s,这些条件计算出d的值,设置d=0.14 m,两种处理都可以确保题目数据严谨自洽.

2 弹簧连两物体的双振子

【例2】(2022年高考全国乙卷)如图2(a),一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上:物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图2(b)所示.已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0.A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同.斜面倾角为θ(sinθ=0.6),与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求:

(1)第一次碰撞过程中,弹簧弹性势能的最大值;

(2)第一次碰撞过程中,弹簧压缩量的最大值;

(3)物块A与斜面间的动摩擦因数.